2019年篮球世界杯球队得分的影响因素

张 滢，余思龙

（华中师范大学 体育学院，湖北 武汉430079）

随着信息时代的发展，数据作为基础性资源，其分析和应用为各领域的发展提供了强有力的支撑，推动了人类社会运转方式、载体和效率的变革。“大数据”自2012年被引入我国以来，热度持续升温。在2018年底召开的中央经济工作会议上，国务院将“大数据”定位为“新型基础建设”，将其视为重要的基础性战略资源［1］。2020年3月4日，中共中央政治局常委会会议明确表明，将“新基建”作为投资发力的主要抓手并且逐年增加比重［2］。由此可见，加快数字基础建设，推动数据资源整合与共享对于促进我国经济建设发展和优化治理体系有着不可或缺的作用。

2019年篮球世界杯在中国举行，这是世界上竞技水平最高、观赏性最强的篮球赛事之一，汇聚了世界各国的顶级篮球强队。但作为东道主，中国队却在家门口与进军奥运会失之交臂，这给处于改革周期内的中国篮球沉重一击。如何充分利用和分析本次世界杯的各项统计数据，厘清世界各强队的制胜因素和技战术特点无疑能为中国男篮提供技术层面的帮助。

数据分析与体育的深度融合对于测定运动员或运动队的优劣并有针对性地制定和优化相应训练计划有着不可或缺的作用。本文运用回归分析的方法来探讨球队的得分的影响因素，将“球队得分”视为因变量，将14 项技术统计指标视为自变量，构建多元回归模型，以期得出各技术统计指标对球队得分的影响程度和作用方式。

1 研究方法和框架构建

1.1 研究方法

1.1.1 文献资料法

以 “2019 篮球世界杯”“篮球世锦赛”“技术统计”“回归分析”等为关键词在中外文数据库进行检索查找相关文献资料。同时在FIBA 官网下载篮球技术统计手册，在图书馆查阅了有关回归分析方法的书籍。对搜集的论著、文献进行仔细阅读和分析，为本研究奠定了一定的理论基础。

1.1.2 录像观察法

通过腾讯体育获得92 场2019 篮球世界杯比赛的录像资料。针对本文所涉及的各项技术统计指标进行抽样统计，仔细观看录像，并结合FIBA 的官方技术统计标准，对所需统计数据进行校准，并且对统计数据进行多次重复统计来减少误差，以确保统计数据的准确有效。

1.1.3 数理统计法

根据技术统计采集与论文需要，本研究采用数理统计法对2019 篮球世界杯球队比赛的球队得分与技术统计数据进行统计，技术统计标准以FIBA2018 版技术统计工作标准为依据。根据研究问题，运用EXCEL 和SPSS25.0 进行数据统计处理，为本研究提供论证依据。

1.2 模型构建

实际比赛中，影响球队得分的因素有多种，通过对影响球队得分的因素进行研究，为球队得分影响因素模型的建立和分析起到重要作用。本文综合分析和总结当前国内外研究成果，以2019 篮球世界杯获胜球队的视角，以国际篮联2019 篮球世界杯比赛官方技术统计标准化面板数据为基础将球队得分的影响因素划分为进攻因素、防守因素两个方面，并结合比赛技术统计数据特点进行数据的整理和校正，最终确定了以球队得分作为因变量，以14 项技术统计指标作为自变量来研究其对球队得分的影响机制。基于上述分析，构建球队得分影响因素模型框架，如图1。

2 结果与分析

2.1 基于多元线性回归分析球队得分影响因素模型验证

利用SPSS25.0，运用线性回归分析，选择球队得分为因变量，两分出手数、两分命中率等14个技术统计指标作为自变量以“进入”的方法进行多元线性回归分析，让所有变量都进入回归模型中。

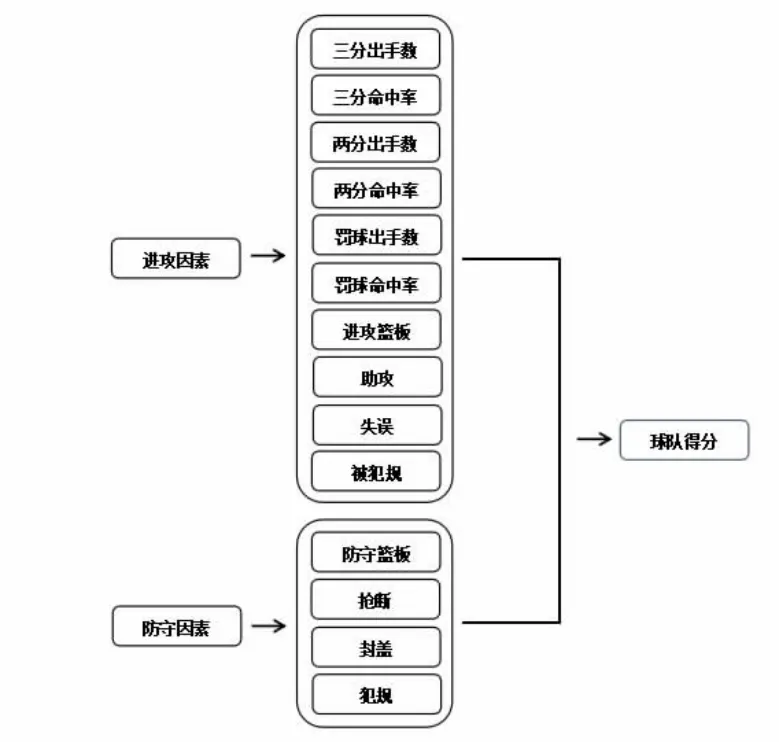
图1 球队得分影响因素模型

2.1.1 回归方程拟合优度评价

表1 多元线性回归模型的估计结果

根据表1 的估计结果，回归模型的相关系数为0.940，判定系数为0.884，表明此回归模型可以解释约88.4%的球队得分变化；调整的判定系数为0.863，与0.884 接近；当自变量数量与研究样本量的比值小于1/5 时，判定系数大概率会高估拟合度，鉴于本研究的自变量数目与样本容量的比值小于1/5，因此倾向于用调节后的判定系数来评价模型的拟合度，即约有86.3%的球队得分变化可以用该模型解释。总体来看，此线性回归模型拟合效果较好。

2.1.2 显著性检验

1）回归方程的显著性检验

在回归方程的显著性检验中，F统计量为41.889，相应的显著性检验值等于0。当P值小于任意显著性水平 （如0.1、0.05、0.01）时，则认为回归方程通过了总检验［3］，回归系数同时为零的假设不成立，表明因变量球队得分与自变量之间存在线性关系，自变量在预测球队得分的多元回归模型过程中数据拟合程度高，可以建立线性回归方程。

2）回归系数的显著性检验

根据表2 的输出内容可得到未经标准化的样本回归方程为：

Y=87.435+4.917X1+4.779X2+5.842X3+5.027X4+4.309X5+1.076X6-0.664X7+0.90X8+2.883X9-0.743X10+0.354X11+1.111X12+0.618X13+0.202X14。

公式中，X1 为A2 即两分出手数，X2 为P2 即两分命中率，X3 为A3 即 三 分 出 手 数，X4 为P3 即 三 分 命 中 率，X5 为FTA 即罚球出手数，X6 为FTP 即罚球命中率，X7 为OR 即进攻篮板，X8 为DR 即防守篮板，X9 为AS 即助攻，X10 为TO即失误，X11 为ST 即抢断，X12 为BS 封盖，X13 为FO 即犯规，X14 为FD 即被犯规；通过观察回归方程的各项系数可知，两分出手数、两分命中率、三分出手数、三分命中率、罚球出手数、罚球命中率、助攻、封盖的回归系数分别通过了t 检验，它们的t统计量分别为6.533、7.266、7.216、8.210、3.735、2.168、2.242，相对应的P值依次为0.000、0.000、0.000、0.000、0.000、0.033、0.028，均小于显著性水平0.05，因此推翻其回归系数为零的原假设。而进攻篮板、防守篮板、失误、抢断、犯规、被犯规的t统 计 量 分 别 为-1.022、0.148、-1.294、0.668、1.152、0.183，相应的P值为0.310、0.883、0.200、0.506、0.253、0.855，大于最大的显著性水平0.1，以0.05 的显著性水平作为衡量标准，自变量进攻篮板、防守篮板、失误、抢断、犯规、被犯规可以认为无法拒绝其回归系数等于零的假设。

综合以上分析，通过观察回归系数显著性中的概率P值，存在显著性P值大于0.1 的情况，可以考虑除去这些不显著变量对模型进行优化，已获得更高拟合度的回归方程。

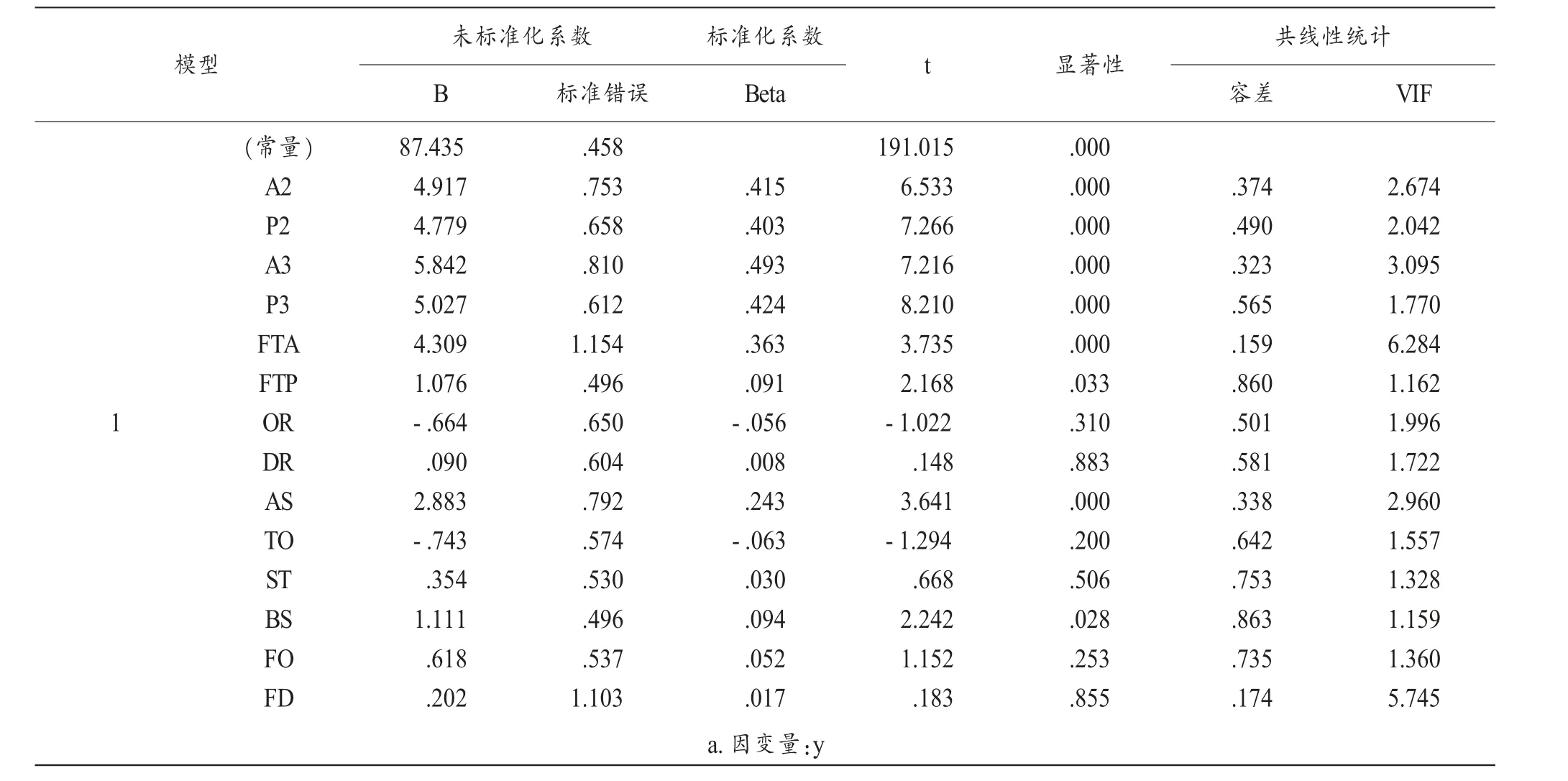
表2 回归系数a 表

2.1.3 回归模型检验

图2 的球队得分的标准化残差直方图显示，球队得分的标准残差分布状况近似服从正态分布，在标准化残差的正态P-P 图（图3）中，因变量的散点位置基本分布位于直线附近，近似一条直线，表明残差近乎是正态的，进而证明误差也近乎是正态的。

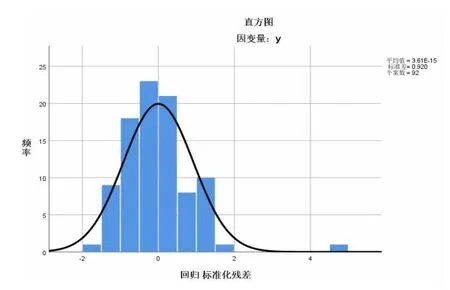
图2 标准化残差直方图

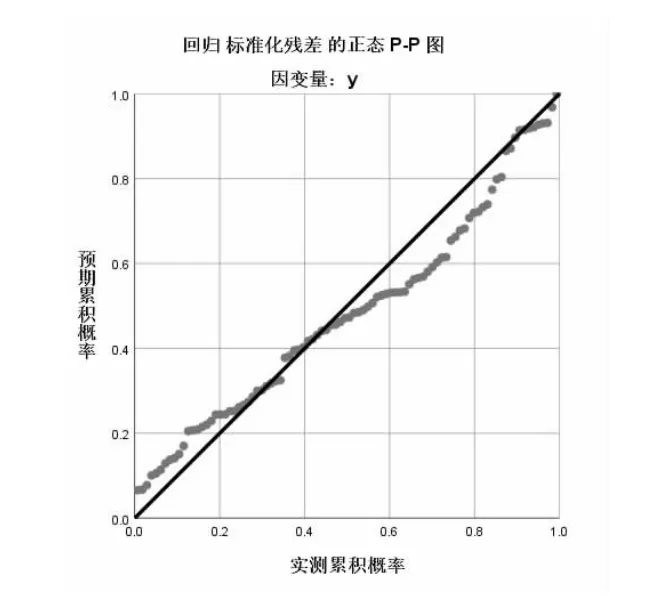
图3 标准化残差的P-P 图

为了进一步验证残差项的正态性，通过K-S 检验以及计算残差统计量的方式来验证残差项的正态性。运用K-S 检验提出一对假设：原假设H0：样本残差服从正态分布；备用假设H1：样本残差不服从正态分布。

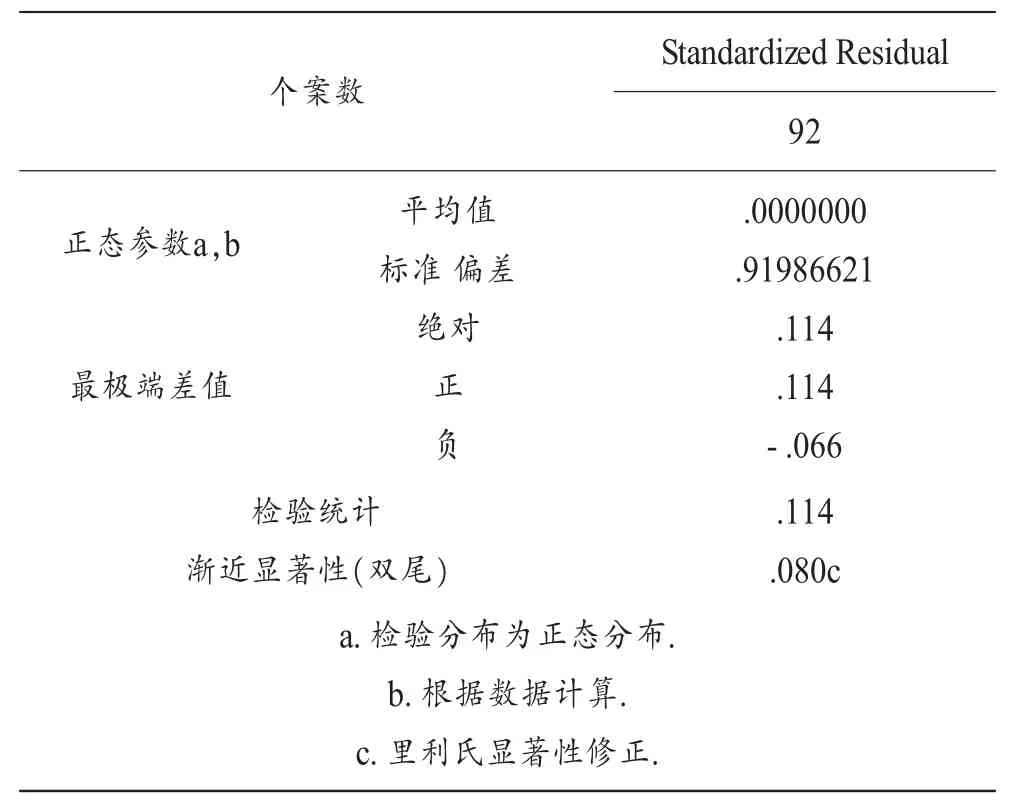
表3 残差项的单样本K-S 检验结果

由表3 中可以看出，样本残差项的均值为0，标准差为0.91986621，对应的P值等于0.08，大于显著性水平0.05，因此必须接受原假设，认为残差项服从正态分布。

2.2 球队得分影响因素模型优化

在上文的研究中，经过多重检验，验证了对于球队得分的多元回归模型是合适的。但回归系数显著性概率P 值存在大于给定的最大显著性0.1 的情况，因此考虑除去这些不显著变量，进一步优化回归模型，本研究尝试利用逐步回归法对变量进行筛选。

回归方程在进行变量筛选过程中，第一个模型由于助攻与球队得分的相关性较强，率先进入回归模型，助攻的t 统计量的观测值为10.210，对应的P值小于给定的显著性水平为0.05［4］，因此，否定回归系数检验的原假设，助攻与球队得分之间存在显著的线性关系。接着，自变量三分球命中率继续加入到之前到一元回归模型之中，t统计量为3.616，P值为0，在结合模型中已有的助攻的基础上，三分命中率与球队得分偏相关系数为0.358，存在显著的线性关系。

由此，逐步加入自变量罚球出手、三分出手、两分出手、两分命中率、封盖、罚球命中率到回归模型中，结果显示，t统计量相对应的P值均小于给定的显著性水平0.05，因此拒绝原假设，回归系数通过了显著性检验。在去除了进攻篮板、防守篮板、失误、抢断、犯规、被犯规6个变量之后，球队得分影响因素模型的自变量筛选过程完成。

根据标准化系数得出标准化的样本回归方程为：

Y=0.232X1+0.434X2+0.397X3+0.499X4+0.435X5+0.424X6+0.092X7+0.091X8。公式中，助攻、三分命中率、罚球出手数、三分出手数、两分出手数、两分命中率、封盖、罚球命中率的标准化回归系数分别为0.232、0.434、0.397、0.499、0.435、0.424、0.092、0.091，Beat 系数的大小可用来比较自变量对因变量的重要性大小。因此，球队得分影响因素的重要程度由高到低依次为：A3＞A2＞P3＞P2＞FTA＞AS＞BS＞FTP（OR、DR、TO、ST、FO、FD 等变量的重要程度排在FTP 之后）。

2.3 球队得分影响因素机理分析

通过分析，回归系数为正的进攻因素大多出现在了回归方程中，这也与实际预期相符。更重要的是，我们得出对球队得分影响显著的因素并做出重要性的排序即三分球出手数＞两分球出手数＞三分球命中率＞两分球命中率＞罚球出手＞助攻＞封盖＞罚球命中率。从研究结果我们可以得出以下信息：

1）三分球、两分球出手数对于球队得分的影响要大于三分球、两分球的命中率。在比赛时间固定的背景下，相较于投篮命中率，越多的投篮出手，将会为球队带来更多的得分。但如果根据研究结果对这些因素做出绝对的强调与忽略，这种无视教练球员主观能动性以及比赛实际情况的做法将使比赛朝着不利的方向发展。因此我们可以理解为实际比赛中，在确保投篮选择合理的条件下，适当增加投篮出手的次数可带来更多的球队得分，同时这也折射出当今世界篮球进攻节奏的加快。

2）三分球重要性突显。在三分球与两分球出手数、命中率的对比中，三分球都是更具优势的一方。对球员的投射能力有了更高的要求，三分球与两分球进攻区域的不同也反映出当今世界篮球潮流下，扩大进攻区域的覆盖范围提升远距离投篮把握能力对球队得分的影响重大。

3）助攻对球队得分影响显著。助攻数的增加说明在比赛过程中，球员在进攻回合积极地传导球，分享进攻球权，使球到达合理的进攻区域与进攻球员的手中。与个人能力较强的球员持球单打相比，通过助攻得分的方式更为简单有效，也充分体现球员之间的相互信任与团结协作。

4）罚球与罚球命中率与球队得分成正相关，即一支球队的罚球出手次数越多、罚球名命中率越高，一支球队的得分也会越高。相较于罚球命中率，罚球出手次数对于球队得分的影响更大，这与各支球队罚球命中率差异较小有一定关系。对于罚球出手来讲，由进攻球员的冲击力、防守球员的防守能力以及裁判员水平所共同决定。从进攻球队的角度来看，如何提升球队进攻的侵略性以及利用对方防守的漏洞来获得更多的罚球对与球队得分乃至最终获得胜利是有所帮助的。

5） 在2019 篮球世界杯中，通过对胜利球队得分进行研究，发现封盖对球队得分影响显著，封盖作为唯一进入模型的防守因素，佐证了进攻与防守相互联系的观点，与其他防守因素类似，封盖能最大限度地阻止对方得分并取得本方进攻的机会，与球队得分成正相关，即越多的封盖会为球队带来更多的得分。

3 结论

通过对2019 篮球世界杯以球队得分为因变量进行回归分析，得出以下结论：

1）三分球出手数、三分球命中率、两分球出手数、两分球命中率、罚球出手、罚球命中率、助攻、封盖与球队得分之间线性关系显著。对球队得分影响的重要性排序为： 三分球出手数＞两分球出手数＞三分球命中率＞两分球命中率＞罚球出手＞助攻＞封盖＞罚球命中率。

2）在球队得分回归模型优化过程中，6个自变量没有通过回归系数显著性检验，对于因变量的影响不显著，即进攻篮板、防守篮板、失误、抢断、犯规、被犯规对球队得分的影响不显著。

3）在当今国际篮球的竞争格局下，对于球队得分来讲，三分球比两分球拥有更重要的战术地位。三分球出手数与三分球命中率对于球得分的影响分别高于两分球出手数与两分命中率。

4）封盖作为防守端的技术统计指标仍对球队得分的影响显著，并与球队得分成正相关。