自主式微航姿系统信息融合方法比较

赵彦明，秦永元，严恭敏

(西北工业大学自动化学院，陕西西安 710129)

0 引言

随着微机械和微细加工技术的发展，各种MEMS传感器日趋成熟，利用微惯性传感器设计微型航向姿态参照系统(micro attitude heading reference system，AHRS)成为现实。自主式微航姿系统(AHRS)具有集成度高、体积小、质量轻、成本低、功耗低、结构简单、可靠性高等优点，所以在很多使用场合被采用，在飞机上常被用作备份的应急测姿设备。微型AHRS一般由三轴MEMS陀螺、三轴MEMS加速度计、三轴MEMS磁强计和信息处理电路组成[1]。其中，MEMS陀螺敏感载体运动角速度，通过求解姿态微分方程来更新姿态角，但是MEMS陀螺存在严重的零点漂移和随机误差，在姿态解算中会产生累积误差，难以满足应用的精度要求[2]。为了实时补偿陀螺漂移和累积误差造成的姿态误差，微型姿态测量系统常同时采用MEMS加速度计和微型磁传感器的测量值，利用信息融合算法，进行传感器信息融合，构建组合姿态测量系统，抑制姿态误差角的发散[3]。

目前有大量文献讨论利用MEMS惯性传感器实现姿态解算的问题，主要分为两类：使用随机线性估计方法，如卡尔曼滤波算法等；使用确定性的互补滤波器算法。

本文对AHRS信息融合算法，包括直接卡尔曼滤波法、间接卡尔曼滤波法和互补滤波器法，进行了算法推导和比较分析，并且应用设计的AHRS系统进行了半物理仿真实验验证，为工程应用中AHRS算法选择提供选择依据。

1 AHRS系统算法原理

设导航坐标系(n系)为“东北天”地理坐标系(g系)，载体坐标系(b系)为“右前上”坐标系。AHRS的姿态更新可以采用四元数形式进行更新，姿态四元数微分方程如下[2]：

(1)

低成本AHRS系统常作为机载应急备份导航系统。由于其MEMS陀螺漂移大，姿态精度较低，需要利用飞机匀速直线飞行时的加速度计输出计算俯仰角和横滚角，结合磁强计输出计算航向角，实时修正四元数更新结果。

(2)

(3)

(4)

考虑磁差和罗差的影响，磁强计输出的磁航向角必须补偿当地的磁偏角α。

2 AHRS信息融合方法

2.1 直接卡尔曼滤波法

根据四元数微分方程和陀螺相关漂移微分方程，建立EKF状态方程：

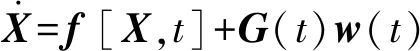
(5)

其中，

(6)

(7)

(8)

将加速度计、磁强计测量值作为观测量。匀速直线飞行条件下，构造量测方程分别如下：

(9)

系统量测方程为

(10)

其中

(11)

式(5)和式(10)构成状态空间模型呈非线性，用EKF进行处理。

2.2 间接卡尔曼滤波法

间接卡尔曼滤波法构建AHRS系统，以载体的姿态误差参数，比如姿态误差四元数或平台失准角作为被估计量，以相对稳定的加速度计、磁强计测量数据为观测量，应用卡尔曼滤波算法进行滤波估计，而后进行误差校正[6-7]。由于平台失准角误差模型具有线性形式，可以直接采用卡尔曼滤波基本方程进行滤波融合，算法简单。选择AHRS系统的平台失准角φ和陀螺漂移εr为滤波状态，即状态向量为：X=[φEφNφUεrxεryεrz]T。构建滤波状态方程：

(12)

式中：F(t)为系统矩阵；G(t)为噪声分配矩阵；w(t)为系统驱动噪声。

(13)

(14)

(15)

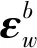
=HfX+Vf

(16)

其中，

(17)

(18)

(19)

(20)

(21)

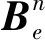
2.3 互补滤波器法

除了卡尔曼滤波算法之外，互补滤波器也常被用于低成本AHRS系统姿态滤波，其具有算法简单，计算量小，实时性高，鲁棒性好的优点，尤其适用于处理器计算资源有限的情况[8]。互补滤波器利用各种传感器量测来相互补充从而获得更好的姿态解算[9-11]。互补滤波器算法原理如下：采用陀螺积分得到的载体姿态和已知的地球重力矢量，解算出地球重力矢量在载体系下的投影和加速度计测量出的地球重力矢量的矢量乘积结果作为水平姿态角的误差表征数值，并且采用比例积分跟踪算法进行误差跟踪反馈，实现了准确的水平姿态角跟踪测量。利用陀螺积分得到的姿态和已知的地球磁场信息，解算地磁场矢量在载体系下的投影与三轴磁强计测量的地磁场矢量叉乘结果作为航向误差角的误差表征数值，并且采用比例积分跟踪算法进行误差跟踪反馈,实现了准确的航向跟踪测量[12]。

(22)

(23)

(24)

(3)计算角速度误差向量

(25)

(4)将δω代入比例积分控制环节，得到载体角速度等效修正量，角速率的总补偿量为

(26)

式中：Kp、Ki分别为比例、积分系数，根据工程经验取值为Kp=0.3、Ki=0.01。

(27)

3 实验验证

3.1 实验说明

利用实验室研发的自主式AHRS系统开展实验，AHRS系统包括姿态测量模块，Micro SD卡数据采集和存储模块，电源模块。姿态测量模块采用九自由度MIMU ADIS16405和STM32F103 ARM处理器搭建。AHRS系统实物如图1所示。MIMU数据输出频率100 Hz，陀螺零偏稳定性26°/h，加速度计零偏0.2 mg，磁强计零偏误差4 mGuass。AHRS系统通过过渡板安装在三轴转台上，如图2所示。初始时刻，系统的姿态角归0，即X、Y、Z轴依次沿东向、真北方向，天向。控制转台依次转到以下测试点，记录各静态测试点的传感器数据：(1)偏航角测试的测试点为：0°、30°、60°、90°、120°、150°、180°、210°、240°、270°、300°、330°、360°；(2)横滚角测试的测试点为：0°、30°、60°、90°、120°、150°、±180°、-150°、-120°、-90°、-60°、-30°、0°；(3)俯仰角测试的测试点为：0°、-10°、-20°、-30°、-40°、-50°、-60°、-70°、-80°、-90°、0°、10°、20°、30°、40°、50°、60°、70°、80°、90°、0°。

图1 AHRS系统实物图

图2 AHRS系统三轴转台实验

从所记录的MIMU数据中选取稳定状态的数据(总时间长6 000 s)。利用实验过程中实时采集的MIMU角速率、加速度和地磁场测量数据进行数据融合算法测试，即分别用直接卡尔曼滤波算法、间接卡尔曼滤波算法、互补滤波器算法处理实测数据，并且对结果进行分析比较。

3.2 实验结果与分析

实验结果如图3～图5和表1所示。其中，图3为采用直接KF滤波法计算的姿态误差曲线，图4为采用间接KF滤波法计算的姿态误差曲线，图5为采用互补滤波器法计算的姿态误差曲线。每幅图均包含3个子图，分别为俯仰、横滚及航向角误差曲线图。表1为3种算法的姿态误差统计结果。

图3 采用直接KF滤波法的姿态误差曲线

图4 采用间接KF滤波法的姿态误差曲线

图5 采用互补滤波器法的姿态误差曲线

(1)表1统计结果显示，在3种方法之中，间接卡尔曼滤波法精度较高，互补滤波器最低，直接卡尔曼滤波法精度居于两者之间。但是3种算法误差处于同一量级，相差不大。

(2)数据离线处理的过程中，用Matlab工具统计各算法的时间开销分别为直接卡尔曼滤波90.264 211 s、间接卡尔曼滤波法183.947 936 s、互补滤波器方法40.540 979 s。间接卡尔曼滤波法时间开销最大，计算量最大，互补滤波器时间开销最小，计算量最小。直接卡尔曼滤波法虽然状态维数比间接卡尔曼滤波多一维，但是由于省去了SINS姿态解算的步骤，计算量小于间接卡尔曼滤波法。

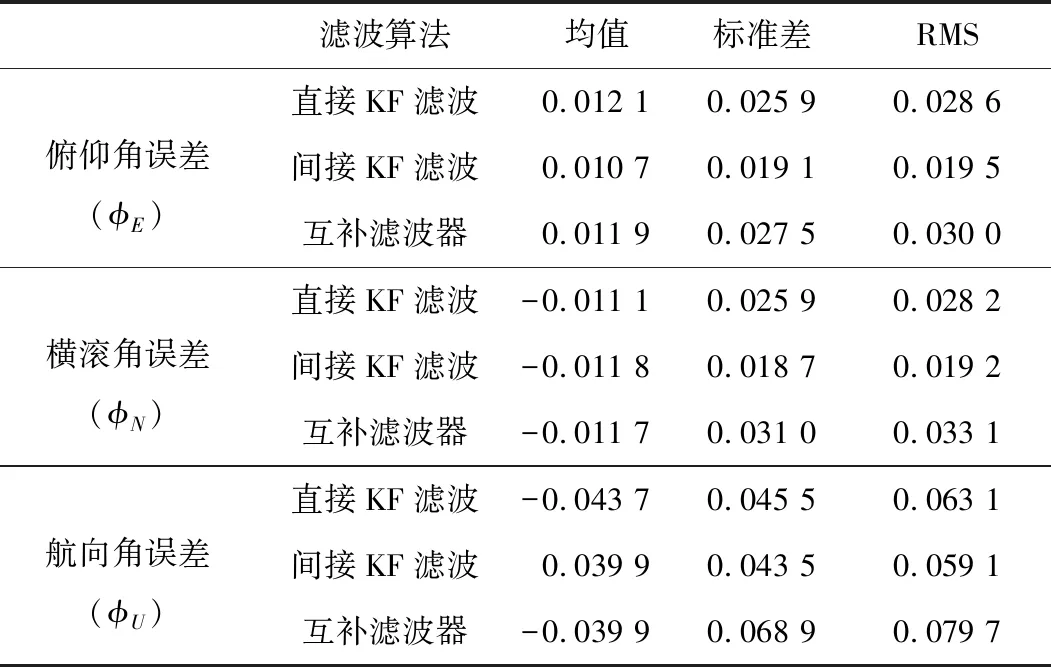
表1 姿态误差统计结果 (°)

(3)KF滤波需要知道精确的滤波模型和滤波参数，如果参数设置不当，或者模型误差大，可能出现滤波发散。互补滤波法利用比例积分控制，使姿态和航向趋于稳定，误差不会累积发散，鲁棒性好。

(4)和KF算法相比，互补滤波器算法简单、运算量小，实时性更好。若AHRS硬件平台采用计算能力有限的单片机，采用互补滤波器更合适。

4 结束语

本文对AHRS系统数据融合算法进行研究，首先对工程中广泛应用AHRS算法，包括直接卡尔曼滤波法、间接卡尔曼滤波法、互补滤波器法，进行了详细介绍，最后利用所设计的AHRS系统进行三轴转台测试，利用采集的MIMU数据对以上3种算法进行试验验证。根据试验结果，对3种算法的精度、计算量和实时性进行分析比较。和KF算法相比，互补滤波器算法简单、运算量小，实时性更好，适用于单片机的AHRS硬件平台。