基于改进的快速密度峰值聚类的调控系统故障定位算法
王 婷,王其兵,燕争上,张秀丽,徐利美,石新聪,
朱燕芳2,强 彦3,郝 伟1
(1.国网山西省电力公司电力科学研究院,太原 030000;2.国网山西省电力公司,太原 030000;3.太原理工大学 信息与计算机学院,山西 晋中 030600)
对电力调控数据中心机房中的设备进行准确故障定位不仅能够帮助运维人员和管理者提高工作效率和掌控能力,而且可以为实际的运维作业与运维管理提供支持。然而,目前电力调控数据中心机房设备的种类繁多,且设备与设备之间相互关联形成一种复杂的结构。此外,不同的设备在运行时产生的数据也存在着错综复杂的关系[1-2]。因此,当其中某个设备发生故障时,如果该故障不能被及时发现处理,将会使得调控数据中心无法正常运行,甚至可能陷入瘫痪的状态,这将造成难以估计的损失。通常情况下,往往采用人工巡查的方式来对调控数据中心机房设备的故障进行检测,这种方式虽然能够从一定程度上降低数据中心设备发生故障的风险,但是由于人工巡检需要根据设备编号逐一进行检查,导致这种方式存在一定的滞后性,效率低。因此,迫切需要一种能够对数据中心设备进行快速且准确的故障定位方法。设备在运行过程中会产生海量的运行数据,这些数据中往往会存在很多异常值,而这些异常值往往就是系统中的异常数据点。通常情况下,这些异常点往往与系统的故障存在密切关系[3-4]。因此,可以通过分析和挖掘不同设备在运行时产生的数据来捕捉这种异常。有效的异常值检测方法可以及时捕捉到调控数据中心系统中的设备的各种异常运行状态,帮助检修人员及时发现并定位故障点位置,从而避免故障扩大,并最大程度的降低经济损失。综上所述,对调控数据中心机房设备产生的海量运行数据进行有效的异常值检测是保证准确定位数据中心故障的关键环节。
基于调控数据中心设备产生的海量运行数据,提出了一种改进的快速密度峰值聚类(IFDPC)的异常值检测算法。具体步骤是首先利用带有递减的本地自适应窗口(LAW)的迭代覆盖图(OM)程序来构建定位图和多维密度图。然后,通过将构建的密度图与原始快速密度峰值聚类算法(FDPC)进行结合来降低后续步骤处理的复杂度。提出的IFDPC算法对参数变化不敏感从而可以对聚类中心的选择过程进行持续优化。在两个不同的电力调控数据中心上的实验结果表明,提出的IFDPC算法能够有效提高故障检测的性能。
1 快速密度峰值聚类(FDPC)算法
对数据中异常点的检测,最常用的是基于聚类[5]的算法。聚类算法的特点是通过识别数据集中的相似样本来形成聚类中心,而异常点通常是距离聚类中心较远的点。聚类算法的计算过程比较复杂的,从算法的角度分析,当聚类的簇数不确定时,聚类问题的复杂性往往是令人棘手。因此,RODRIGUEZ et al[6]提出了快速密度峰值聚类(FDPC)算法,该算法能够处理非球面形状数据,并提供了一个方便的决策规则来找到正确的聚类簇数[7]。该算法将聚类中心定义为具有局部密度最大值的位置点。更具体地,聚类中心具有以下特点:1) 聚类中心被具有更低密度的邻居点包围;2) 这些邻居点远离任何具有更高密度其他点。因此该算法主要关注的因素有两个:局部密度和与更高密度点之间的距离。FDPC算法主要包括下述过程。
1) 首先选择距离dc,并将其用于定义邻居点。通过计算比dc更靠近的样本点xi的数量来计算每个数据点xi的密度ρi.
2) 对于每个数据点xi,找到密度ρi较高的最近点,并记录能够将它们分开的最短距离δi.
3) 聚类中心定义为同时具有高密度ρi和较大距离δi的点xi.令(xi)i=1…N为样本点。在FDPC的第一步中,计算每个数据点之间的欧几里得距离dij.然后,选择距离dc,最后为每个xi计算比dc更接近点xi的数据点的数量。然后根据下式获得局部密度:
(1)
式中:K是核函数。在第二步中,计算点xi和任何其它具有更高密度的点之间的最小距离,如下式所示:
(2)
最终,聚类中心(δ,p)在形成的决策图中被定义为离群点,这些离群点同时具有较高局部密度ρi和较大距离δi,而异常点则往往是具有极低局部密度和较大距离的点,即这些点会独自成簇。通过将这些点找出并逐个进行标记,从而完成在计算量较小的情况下,快速找到异常点的目的。
2 改进的快速密度峰值聚类算法
虽然,FDPC算法取得了很多成就[8-15],但是将其应用于电力调控数据中心设备的异常值检测仍然面临很多挑战:
1) 在PDFC算法步骤(1)中,需要计算所有样本点之间的距离,从而导致算法复杂度很高和较大的内存占用量,在其他步骤中也面临同样的情况。在面临电力调控数据中心设备产生的海量运行数据时无法进行快速且有效的处理。
2) 阈值距离dc的选择往往需要依靠个人经验,这严重影响了聚类算法的最终结果。
3) 决策图中异常值的确定没有统一的规则,从而导致对聚类中心的选择需要依赖手动或仅仅是半自动的。
鉴于此,本文提出了一种改进的快速密度峰值聚类(IFDPC)算法以克服上述缺点,整体流程图如图1所示。 IFDPC的总体思路是,首先通过使用递减窗口的迭代覆盖图OM过程来构建密度图,减小问题的维数N,然后使用它提供的定位信息来改进步骤(2)和(3).该算法在处理非球面数据方面继承了FDPC算法的高效性和准确性,并且可以考虑采样点与相邻采样点之间的关系,从而大大减少了聚类中心的选择和标记的计算,显著提高了对异常点检测的准确性。

图1 改进的快速密度峰值聚类(IFDPC)算法流程图Fig.1 Flowchart improved fast density peak clustering(IFDPC)algorithm
2.1 构建密度图和决策图
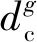
2.2 程序覆盖图(OM)
对于给定的固定窗口dc,OM的迭代过程使用半径为dc的球域来搜索整个数据集。第一个观测值x1用于构造第一个球B1(x1,dc);然后,对于每个观测值xi,首先检查其是否至少属于一个现有的球即计算xi与球心x1的距离是否小于半径dc.如果是,则该球B1(x1,dc)的密度计数增加一。否则,将创建一个新的球Bk(xi,dc),整个迭代计算过程如算法1所示。经过该迭代过程,最终获得一个球集。该集合中包含的数据点数量将比原始数据集中包含的数据点数量少得多,并且该集合中每个数据点的局部密度ρi组合在一起能够覆盖整个原始数据集。

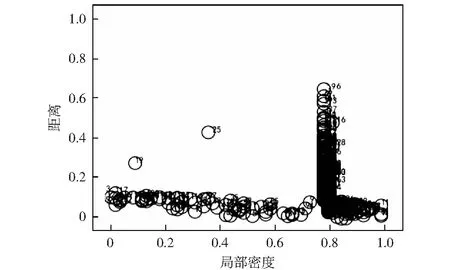
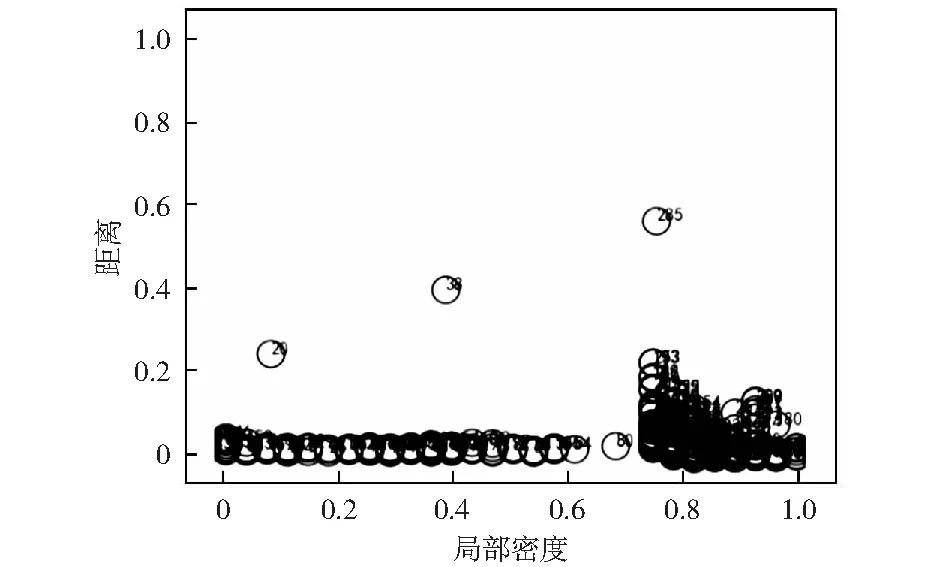
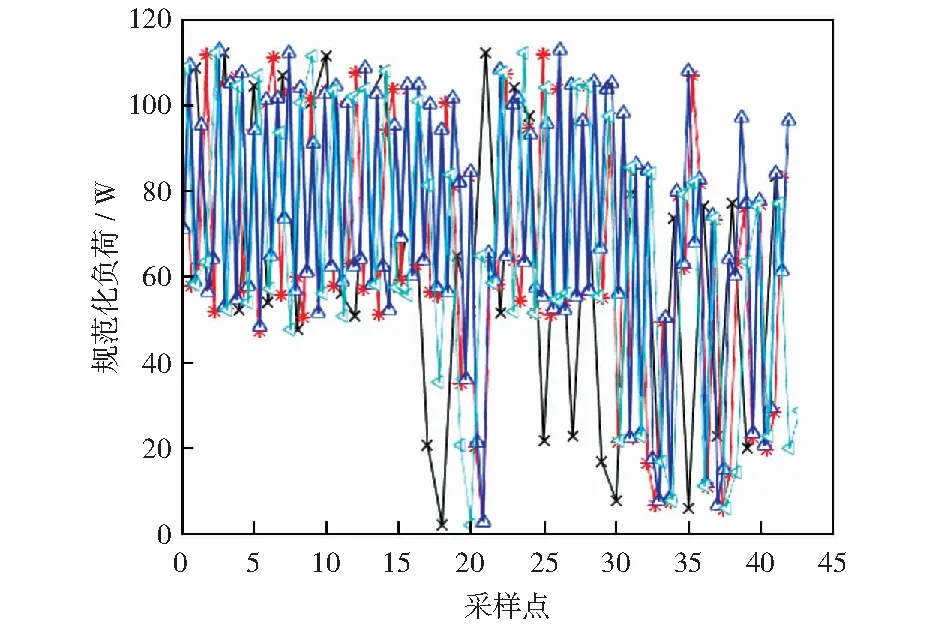
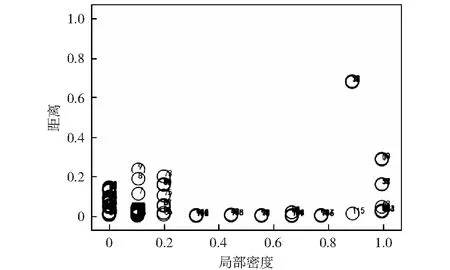
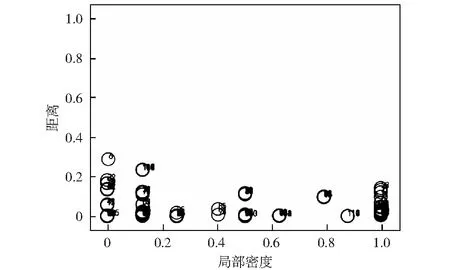
算法1:OverMap开始:OM(dc)OM 创建第一个球: S←B1(x1,dc) ρi(B1(x1,dc))←1 创建新球: forallx1,i>1do d←distance(xi,S) J←{j|d[j] 索引J将被储存,从而能够加载xi的母球并知道xi是否在下一个OM迭代中属于该球域。在对所有观测值xi进行处理之后,Nmin个点被设置为终端球的数量。然后,通过对得到的球点集合进行最后一次遍历来重新评估密度计数。具体的,对于每个点xi,首先找到xi所属的第一代球,将其密度计数增加1,之后加载距离xi更近的球的子代,重复该过程,直到xi不属于任何一个球的子球。通过以上操作,可以获得对于每个数据点xi,包含它的距离最近且局部密度较小的终端球cci. 计算完每个点的ρi和δi后,使用δi作为纵坐标,ρi作为横坐标来画出决策图,其中决策图右上方的点就是簇的中心点,右上方有几个点,就意味着分为几个簇。聚类中心的选择和标记的主要目标是为每个终端球找到距离最接近且局部密度最高的球作为该终端球所属的聚类中心。具体的筛选过程如下:1) 密度非常低的点通常是噪音点,独自成簇,可做好标记,不参与后面的分配;2) 可选择两个指标都在前50%的成立簇中心,剩余的每个数据点都被标记为包含它的最近的终端球。至此,整个聚类操作就结束。 在本实验中,使用C语言进行实验仿真。为了评估提出的IFDPC算法的有效性,收集了两种类型的某电力调控数据中心机房设备运行数据,并进行仿真实验。 首先从数据中心的每台设备上(包括处理器,内存和I / O, 设备温度等)获得一组相同的性能参数作为构建的预测模型的输入,如表1中所示。这组预选参数将被定期收集,其值可以作为预测硬件故障的可靠指标。采样频率为1 h,即每天采集24个采样点,采样时间为2018-07-28-2019-07-27,共365 d。此外,在得到原始的参数数据之后,首先对数据采用最大最小值归一化方法[16]进行归一化以消除由不同量纲的数据样本对结果的不利影响并加快模型的训练速度。然后,采用本文提出的IFDPC算法进行实验。首先对从电力调控数据中心设备上收集的性能参数曲线进行可视化,结果如图2所示。从图2中可以看出该调控系统大部分曲线都趋向于正常状态,仅存在少量异常情况,这说明系统在大部分时间下都处于正常状态,而当系统出现异常时,收集的设备性能参数会与正常模式有很大的偏差。这些偏差数据正是算法要找出的异常点。这说明,提出的算法可以很好地捕获调控系统中设备运行异常点,从而可以帮助管理人员快速定位故障位置。 表1 从数据中心收集的每台设备的性能参数Table 1 Performance parameters for each device collected from the data center 图2 电力调控数据中心设备的性能参数曲线Fig.2 Performance parameter curve of power-regulated data center equipment 为了更好地展示提出的IFDPC算法的优势,与原始FDPC算法相比,分别绘制了这两种算法在进行故障定位时的决策图,如图3和图4所示。其中图3为原始FDPC算法获得的决策图,从图3中可以看出,调控中心设备性能参数样本集中只有一个明显的聚类中心,而其他聚类中心则相对不明显,这正符合原始的FDPC算法的特性,对于局部密度变化较大的数据该算法的识别能力较弱,因此,峰值密度较低的点可能被忽略或视为异常值。 图3 案例一的原始FDPC算法的决策图Fig.3 Decision chart of the traditional peak density clustering algorithm of case 1 图4是提出的IFDPC算法获得的决策图,图5为该算法实验密度图。从图4中可以看出,提出的IFDPC算法能够准确检测到图2中的异常曲线,而这些曲线则是与正常模式不同的设备异常情况。此外,从图4中可以明显看出,在处理局部密度变化较大的数据时,IFDPC算法与原始的FDPC算法相比结果有明显提升,决策图中右下角最明显的聚类中心以及其他聚类中心,图4中样本点的3个特征值比图3中更为明显,这意味着IFDPC算法获得的聚类中心比原始FDPC算法更加准确。 图4 案例一的IFDPC算法的决策图Fig.4 Decision chart of improved fast density peak clustering algorithm in case 1 图5 IFDPC算法的密度图Fig.5 Density chart of improved fast density peak clustering algorithm 此外,为了证明提出的IFDPC算法在以日为单位的采样情况下也能准确地捕获设备异常情况,从2018年7月28日-2019年7月27日,获得了365条设备日性能参数曲线,结果如图6所示。从图6中可以看出,提出的IFDPC算法能够从365条设备日性能参数曲线中准确找到具有异常情况的7条曲线,显示出IFDPC算法对设备异常值检测的出色性能。此外,图6中的结果还说明了IFDPC算法可以有效解决FDPC算法在识别局部密度变化较大的数据时能力较弱的问题。 图6 案例一的电力调控数据中心设备的性能参数日曲线Fig.6 Performance parameters of power control data center equipment in case one day curve of case 1 为了在多种情况下比较本文提出的IFDPC算法的优势,在另一个数据集上再次进行实验对比。该数据集中的样本来自2017年-2019年某电力调控数据中心机房设备产生的运行数据,数据的类型与表1中相同。该数据的采样频率为7 d.分别使用原始FDPC算法与提出的IFDPC算法进行实验。图7是原始的FDPC算法获得的决策图,从图7中可以看出,在初始时间点位置0.0~0.2的数据具有相对密度和距离相对较大的特点,并且出现了环形现象。这显示了原始的FDPC算法在处理复杂数据时存在一定的局限性。 图7 案例二的原始FDPC算法的决策图Fig.7 Decision chart of the original fast density peak clustering algorithm of case 2 图8是提出的IFDPC算法获得的决策图。图中在初始时间点位置0.0~0.2的数据的环形现象基本消失,获得的聚类结果明显优于原始FDPC算法,并且IFDPC算法获得的聚类中心的特征更加明显。由于调控数据中心机房设备产生的数据往往是局部密度变化较大的数据类型,因此,以上实验结果充分表明了提出的IFDPC算法在处理调控数据中心机房设备数据时的优势。 图8 案例二的IFDPC算法的决策图Fig.8 Decision chart for improving fast density peak clustering algorithm of case 2 此外,由于数据集二中的异常值分布在不同的年份,因此,无法直观地用曲线来表示它们。为了更加直观地观察获得的异常分布,根据提前制定的异常值判定规则,获得了数据集中的异常值分布,结果如表2所示。从表2中可以看出,提出的IFDPC算法可以成功检测到数据集二中的所有异常值,这些异常值的数量大约有13个。结果表明,相比于原始的FDPC算法,提出的IFDPC算法更加关注在不同年份下同一时期内的调控数据中心机房设备产生的运行数据的纵向对比。更近一步,IFDPC算法将注意力重点放在数据集中所有数据的局部变化上。通过在调控数据中心不同类型的机房设备产生的运行数据上进行实验,结果表明提出的IFDPC算法对局部密度变化较大的数据类型的异常值检测具有很好的效果,这说明了提出的IFDPC算法的有效性。 表2 获得的异常值的分布列表Table 2 Distribution list of obtained outliers 提出了一种改进的快速密度峰值聚类算法(IFDPC),该算法在原始快速密度峰值聚类算法(FDPC)的基础上,采用带有递减的本地自适应窗口(LAW)的迭代覆盖图(OM)程序来构建多维密度图和决策图,并将构建的密度图与FDPC算法进行结合显著减少了后续步骤处理的复杂度。实验结果表明,提出的算法对电力调控数据中心的机房设备的故障检测达到了较高的准确率。2.3 窗口尺寸递减的迭代OM(LAW)



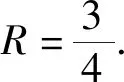
2.4 聚类中心的选择和标记
3 实验与结果
3.1 实验一

3.2 实验二

4 结语

