基于教材的小学数学拓展课程设计原则
童义清
摘 要 小学数学拓展课程,是基础课程的有益补充,是发展小学生数学核心素养的重要载体。基于教材设计小学数学拓展课程,须保证课程设计基于真实学情,目标清晰明确;确保基础课程到拓展课程的过渡由易到难,且拓展课程本身也应由简单到复杂;兼顾拓展课程内容的典型性和解决问题策略的典型性,帮助小学生“见‘少识‘广”;提升拓展课程的吸引力,达到“有意义且有意思”。
关键词 教材 小学数学 拓展课程 设计原则
小学数学拓展课程,作为基础课程的有益补充,它是儿童进一步探索新知识的材料、进一步提升核心素养的载体,更是进一步感悟数学魅力的平台。然而就普通小学数学教师而言,限于课程研发理论、研发经验和实施条件的束缚,“基于教材—因需设计—班本实施”,不失为一种灵活实用的拓展方式。下面,笔者就从教材的角度谈谈小学数学拓展课程设计的基本原则。为了方便交流,以苏教版《数学》六年级下册“圆柱的表面积”为例,分享笔者设计的“多变的圆柱表面积”这一拓展课。
一、目的性
有的放矢,是研发和设计拓展课程的基本原则。为什么要设计“多变的圆柱表面积”这节拓展课呢?这是因为笔者发现:对六年级的学生而言,“圆柱的表面积”这一课学生学得既“不过瘾”,也“不彻底”。
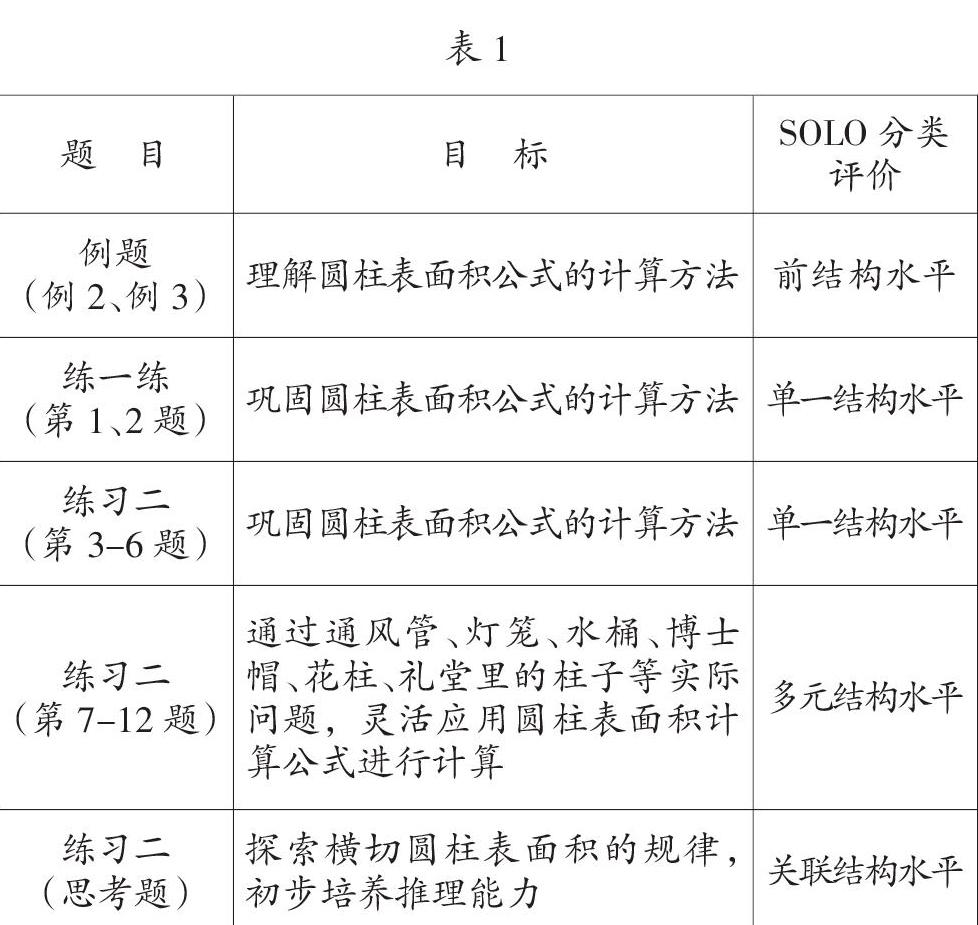
苏教版教材在这一节内容安排了2道例题和13道练习。根据SOLO分类评价水平,笔者对这些例题和习题做了如下分析。
苏教版数学教材的这种编排,难度层次分明,重点难点突出,“四基”导向鲜明,是一种非常理想的基础课程。合肥市城区的六年级学生起点整体较高,每个班级至少有60%的学生在校外教育机构参加数学拓展课程学习。所以,从学生的真实学习情况来看,教材上的这2道例题和13道练习题,留给学生的经验仅仅还停留在“求一个完整的圆柱体表面积”和“求缺少1个面或缺少2个面的圆柱体表面积”,留给学生的印象多是枯燥繁杂的计算、人为设置的单位换算、近似数如何取值等相对固化的要求。生活中,还有大量的、美妙多变的圆柱表面积问题得不到注意,与他们认知需求相适应的拓展内容得不到补充,学生的视野和思维得不到最大程度的提升,这不得不说是一种客观而真实的缺憾。
因此,笔者综合了圆柱表面积问题的各种情形,提炼和设计了“多变的圆柱表面积”这一拓展课,内容包括“组合圆柱的表面积”“切割圆柱的表面积”“卷旋圆柱的表面积”三个拓展内容。这三个拓展内容,基本覆盖了小学生可以接受的圆柱表面积的所有问题,可以帮助学生“学得过瘾”“学得彻底”。
二、层次性
美国教育心理学家加涅认为:“人类的学习是复杂多样的,是有层次性的,总是由简单的低级学习向复杂的高级学习发展,构成了一个依次递进的层次与水平。”小学数学拓展课程,既要与基础课程形成层次性,其自身又要具有层次性。
第一,拓展课程与基础课程形成层次性。苏教版数学教材上的基础课程,重在引导学生理解表面积的计算方法,通过2道例题和13道练习题,主要训练学生应用公式的能力,教材突出的是基础知识和基本能力;“多变的圆柱表面积”一课不再是简单的记忆公式、理解公式、应用公式,而是融入了分析、创造等高阶思维活动,无论是解答过程、方法的复杂程度上,还是内容和思维的要求上,都有了更高的要求。
第二,拓展课程自身具有层次性。“多变的圆柱表面积”课程内容,从情境原形上看,“组合圆柱的表面积”属于静态问题,学生直观可见;“切割圆柱的表面积”属于动态问题,学生理解难度有所提高;“卷旋圆柱的表面积”则是需要借助思维想象的问题,对学生的空间观念要求较高。这三个拓展内容,难度逐渐升级,思维抽象程度不断递进。从内容结论上看,“组合圆柱的表面积”规律明显,变式不多,学情基础好;“切割圆柱的表面积”规律较明显,变式较多,学情基础较好;“卷旋圆柱的表面积”规律不明显(如用一张长方形纸,横着卷形成的圆柱表面积比竖着卷形成的圆柱表面积小的规律是:■-■),学情基础不足。所以,这种层层递进的拓展课程设计,遵循了儿童学习由易到难的规律,符合儿童认知事物的基本特点。
三、典型性
设计什么样的拓展课程,才能让学生“见少识广”呢?拓展课程具有良好的典型性,是不二选择。典型课程,既要做到内容典型,还应兼顾到解决方法的典型。如果一道拓展习题能够代表一类拓展内容,一节拓展课能够折射一个体系的拓展精髓,是设计小学数学拓展课程的理想境界。
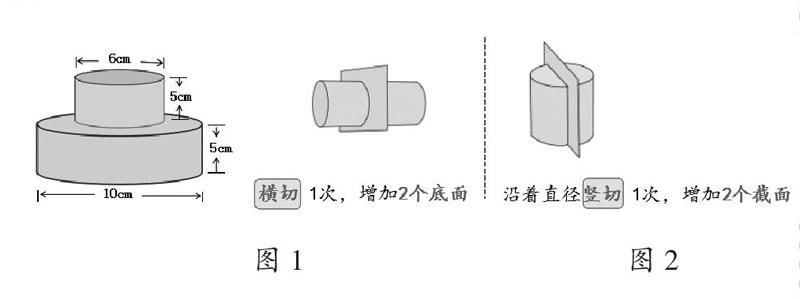
“圆柱的表面积”涉及问题多,具体的例子、情境更是数不胜数。笔者从“组合圆柱”“切割圆柱”“卷旋圆柱”三方面进行提炼,并通过典型内容的呈现,引导学生进行探究,从而发现其中的规律,掌握解决的方法,最终建立良好的数学模型。比如,在“组合圆柱的表面积”这个拓展内容中,笔者设计了求“一大一小、上下叠放的组合圆柱表面积的问题”(见图1),并组织学生自主探究解决方法。这种组合形式是最基本的组合,当然也是最典型的组合。学生在解决这个问题的过程中,一般会出现两种思路:思路一是“S组表=S大表+S小表-2S小底”,思路二是“S组表=S大表+S小侧”。两种思路,体现了解决组合圆柱表面积问题的两种典型方法:“面积加减法”和“抵消转化法”。这种典型内容和典型的解答方法,都有利于学生形成解决类似问题的“基本活动经验”。再如,在“切割圆柱的表面积”这个拓展内容中,笔者通过与学生研究“横切圆柱”和“竖切圆柱”后表面积变化的典型规律(见图2),引领学生深度理解和建构“切割圆柱的表面积”问题的基本模型。
四、趣味性
如何增强拓展课程的吸引力呢?拓展课程的深度和广度都胜过基础课程。加强课程的趣味性,不但是基础课程的要求,更是拓展课程的“刚需”。作为课程的设计者,我们需要准确把握不同学段儿童的兴趣点,有效提升课程吸引力。比如,面对第一学段的儿童,我们可以在形式上体现趣味,以增强课程的吸引力;针对第二学段的学生,我们可以在内容上和方法上体现趣味,以更好地吸引学生参与学习。
在“多变的圆柱表面积”一课中,三个内容因为体现了三种不同的乐趣,受到了学生的欢迎。“组合圆柱的表面积”,体现“挑战之趣”。接受最近发展区内的挑战,是每个人与生俱来的好奇心理和进步心理。学生学习基础课程时,一旦掌握了计算公式,接下来就是翻来覆去地应用在一个又一个圆柱上,有的要计算3个面,有的要计算2个面,还有的只要计算1个侧面。学生一旦遇到需要计算两个圆柱或者多个圆柱组合的表面积,必然会产生挑战的乐趣,这种乐趣驱动学生主动积极地投入到一个新知探索的过程之中。“切割圆柱的表面积”,体现“思考之趣”。与基础课程相比,把一个圆柱“横着切”“竖着切”,而且研究“截面”,这不是像做游戏一样,很有趣的一种思考活动吗?在這种带有儿童游戏色彩的思考过程中,去建构数学模型,对每位学生来说都有强烈的思考乐趣。“卷旋圆柱的表面积”,体现“操作之趣”。皮亚杰说:“儿童的智慧,发源于指端”,同样,儿童的乐趣,也源自指端。真实可见的普通纸张,通过横着卷、竖着卷,横着旋转、竖着旋转都能形成圆柱体,这不是很神奇吗?更重要的是,学生还能通过趣操作之后的冷思考,找到表面积大小的规律,让好玩的操作成为探寻数学结论的素材。
小学数学拓展课程的设计,从不同的维度和视角,还有许多需要注意的地方,比如系统性问题、科学性问题、针对性问题、评价性问题等等。这些都值得我们在具体实践中不断探索、不断总结,从而为儿童数学核心素养的真正落地做出我们应有的贡献。
[责任编辑:陈国庆]

