基于尺度自适应的小波变换LIBS谱峰识别算法

吕罗庚，史晋芳，邱 荣，邓承付，郭旺林

（1.西南科技大学 极端条件物质特性联合实验室，绵阳 621010；2.西南科技大学 制造科学与工程学院，绵阳 621010；3.西南科技大学 制造过程测试技术省部共建教育部重点实验室，绵阳 621010）

0 引言

激光诱导击穿光谱技术（LIBS）是一项发展迅速的光谱分析新技术，其通过脉冲激光轰击样品形成等离子体，分析收集到的等离子体光谱从而实现元素的定性与定量分析。其中，寻峰算法的准确度和自动化程度是保证激光诱导击穿光谱定性与定量分析检测精度和自动化程度的关键[1,2]。目前在信号处理和光谱分析领域常用的寻峰算法包括导数法[3]、高斯曲线拟合法[4]和连续小波变换法（CWT）[5～11]等，其中，因不需预处理过程，CWT算法应用范围相对较广[5]。

在CWT算法中，尺度参数的选择至关重要[6～10]，目前针对尺度选择方法的相关研究并不多。在传统的CWT算法中，尺度参数的取值范围都很大[6,7]，其结果是在造成资源浪费的同时寻峰能力也不强。针对尺度如何选择的问题，陈鹏飞等[8]探讨了尺度参数的取值方法，提出尺度参数的选择依赖于光谱半高宽经验值；Zheng等[9]分析了尺度选择对寻峰的影响并探讨了谱峰标准差与半高宽的关系；Gregoire等[10]使用以1.18为底数的对数函数确定尺度范围，并探讨了尺度上下限的取值方法。上述文献中的尺度选择方法都是针对特定情况靠人工方式设定，应用环境一旦改变，尺度参数设置就会繁琐且困难。如何自动的进行尺度选择以使CWT算法适应不同环境下的寻峰需求是一个亟待解决的问题。本工作针对尺度自动化调整的问题，探讨了尺度选择对连续小波变换的影响规律，在传统CWT算法的基础上提出尺度自适应（SA-CWT）算法，并对SA-CWT生成的小波系数矩阵进行局部阈值优化并应用Gaussian-LM谱峰判定法完成对谱峰的自动识别。通过实验比较了3种寻峰算法的应用效果，证实了本算法对于LIBS元素分析过程中的弱峰和重叠峰识别具有一定优势。

1 尺度自适应寻峰模型

1.1 连续小波变换模型

LIBS光谱的线型主要呈佛克托（Voigt）型[2]，但在实际分析中为了便于计算一般采用高斯（Gauss）线型，表示为：

LIBS光谱信号f(t)的连续小波变换定义为：

式中：s为缩放尺度；u为平移参数；C为小波系数；ψu,s（t）为小波母函数ψ（t）经缩放平移得到。其中，本工作选择Mexican小波作为小波母函数，表达式为

1.2 尺度自适应模型

确定尺度参数取值极限smin、smax：

式(2)能被重写为多尺度微分算子（MDO）形式[11]：

按Nguyen等人[12]提出的方法构造过零线求得峰位ui和标准差7σi，由si=2.237×7σi计算得到每个波峰处的最佳尺度。绘制关于尺度的概率分布图，取5%和95%分位数时的尺度分别作为smin、smax。

最后，在最值范围内等差取20个值组成新的尺度参数向量，表示为：

2 寻峰方法

将尺度自适应模型引入到CWT脊线寻峰中，提出基于尺度自适应的SA-CWT寻峰算法。其算法流程如图1所示，实现步骤如下：

步骤一：SA-CWT

1）第一次CWT运算：尺度按文献[8]的方法以1.18指数增长，选择从1～23.2共20个尺度进行CWT运算得到小波系数矩阵；

2）尺度调整：上一步骤所得的小波系数矩阵带入自动尺度选择模型确定新的尺度向量；

3）第二次CWT运算：以新尺度向量进行CWT运算得到新的小波系数矩阵。

步骤二：局部阈值优化

使用新小波系数矩阵进行CWT脊线寻峰，在脊线构造中，通过比较局部信噪比过滤由噪声引起的小波系数局部极值。

步骤三：谱峰判定

应用基于曲线拟合的Gaussian-LM[13]算法代替信噪比阈值法对真实峰进行筛选。

3 实验与讨论

3.1 实验数据制备

激光器（Innolas，Spitlight 600；1064nm，1Hz，108mJ）产生激光经由透镜聚焦于样品表面下方2mm处，轰击产生的等离子体发光由透镜汇聚并经光纤探头采集传递到中阶梯光谱仪（LTB，Aryelle200）和ICCD（Andor，i-star）中分别进行分光和光谱采集操作，最后采集到的数据在计算机（i5-7500，16G）上进行显示和分析。其中，ICCD延迟时间1.5us，积分时间5.0s，门宽0.5us；样品是标准土壤（GBW07387，GSS-31）、PE微粉、纯化合物PbTiO3和BaTiO3压制成的圆饼状薄片（1φ12mm×2.3mm）。将样品配置成浓度不同的7组，每组Pb、Ba含量如表1所示，实验时每累积10发采集一次数据，对不同浓度含量下的光谱各采集20张并取平均（多张取平均是为了消除随机噪声）得到7组数据，图2所示为C4浓度下的光谱数据。

图1 基于SA-CWT的寻峰算法流程

表1 Pb和Ba实验样品浓度

图2 C4浓度下原始光谱

3.2 尺度调整实验

图3为尺度参数对谱峰小波系数的影响图。其中，图3(a)、图3(b)、图3(c)分别对应不同波长下强峰、弱峰和重叠峰的数据及其高斯拟合光谱图；图3(d)、图3(e)、图3(f)是尺度按文献[8]取值时其对应的小波系数效果图；图3(g)、图3(h)、图3(i)是经尺度自适应模型调整后其对应的小波系数效果图。由图可以看出，对于孤峰（无论是强峰还是弱峰），每个峰都有其对应的最佳尺度，并在最佳尺度处小波系数值最大，且该最佳尺度与每个峰的高斯拟合标准差之间大约成2.237倍关系；而对于重叠峰，由于受叠加效果的影响，其最佳尺度远小于标准差的2.237倍。比较尺度调整前后的小波系数效果图，对于弱峰和重叠峰识别，尺度按文献[8]取值时，随着尺度逐渐增大会出现复合脊线的情况从而影响寻峰准确度，而尺度范围经尺度自适应模型调整后不但提升了寻峰的准确度，而且排除了大尺度对寻峰的干扰问题从而提高了寻峰精度。因此，对于脊线寻峰模型来说，只需确保尺度取值范围在最佳尺度内就能保证对峰的正确识别，即经过尺度自适应模型调整后的尺度更能提升CWT脊线法对弱峰和重叠峰的识别能力。同时，通过尺度自适应模型能一次性调参到位，从而避免了麻烦的调参过程，节省了时间并提高了自动化水平。

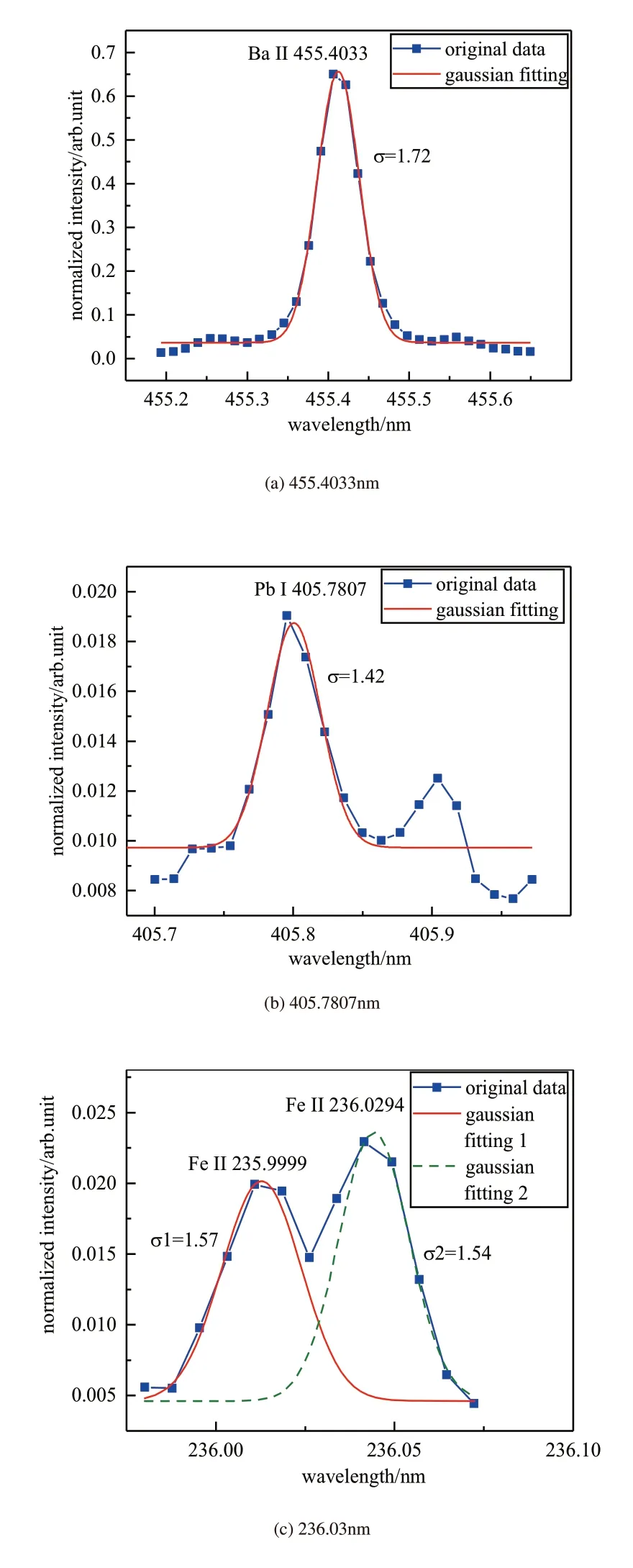
图3 尺度参数对谱峰小波系数的影响

3.3 寻峰实验

在Matlab2016b平台下，为检验本算法对弱峰和重叠峰识别的准确性，对真实LIBS光谱数据进行实证分析。对含Pb、Ba的LIBS光谱进行寻峰实验，每张光谱选择波长范围在（235.5nm～236.5nm、405nm～406nm、455nm～456nm）之间的光谱段进行演示，共计270个数据点。分别应用高斯拟合法、小波脊线法和本算法进行寻峰实验。

图4是C4浓度下三种寻峰方法对实验数据的寻峰效果图。由图可以看出，相较于高斯拟合法和CWT算法，本算法的寻峰效果更优。其中，对于强峰，三种算法都能正确识别；对于弱峰，高斯拟合法与CWT算法识别出了许多因噪声引起的假峰，且对于波长455.8015 nm和455.9836nm处的两个真实峰，高斯拟合与CWT算法都没有成功识别；对于重叠峰，三种寻峰算法也都能正确识别，但对于波长236.0108nm和236.0416nm处的两个重叠峰的识别结果中，CWT算法错误的引入了第3个峰。表2为本算法识别出的具体峰位数据，由表可以看出，本算法的寻峰结果与NIST查询结果基本一致，峰位误差在0.0143nm左右，寻峰精度较高，能够满足LIBS定性与定量分析的要求。

表2 本算法和NIST的峰值对比表

图4 C4浓度下三种寻峰方法的寻峰效果

4 结语

在连续小波变换的基础上，分析与探讨了尺度参数选择的意义，提出了尺度自适应寻峰算法。该算法通过尺度参数自适应调整提升了CWT算法对弱峰和重叠峰的识别精度，并应用阈值优化和Gaussian-LM谱峰判定法实现了LIBS光谱的自动寻峰过程。结合实验结果，该算法避免了重复繁琐的人工尺度参数调试工作，缩短了实验周期；同时具有寻峰准确度高、弱峰和重叠峰识别能力强等优点。