同塔多回输电线路动态物理模型设计

王 卓，刘靖辉，张慧超

（中国计量科学研究院，北京102200）

0 引言

随着社会日益发展，输电线路走廊紧张已成为不争之事实。同塔双回线路可以节约大量的输电走廊面积，其建设已成为必然的趋势。然而由于同塔多回线路导线数目众多、线路距离近而容易引起跨线故障，因此对现有保护影响严重，给电力系统的运行带来极大的挑战。为了保障电力系统的安全运行，需要开展相关继电保护的研究及建设保护装置，而装置研制的前提需要满足理论研究的结果[1]。

现有的同塔多回输电线路物理模型多是根据单回线或普通平行双回线的特性而研制，并不能准确模拟同塔多回线路各导线之间的耦合，此时对于继电保护研究也就不能真实反应实际的动作需要。与此同时实际模型研制困难、成本高、参数调整难度大，对设备提出了较高要求[2]。

为此文中提出了一种以π型模型为基础，全面反映线间互感，减少互感器数量的同塔多回输电线路参数模型，具有节约成本、经济便捷的特点。通过参数计算、故障及对外特性实验，论证了模型可行性，可为相关继电保护的研究和装置的研制提供理论基础。

1 输电线数学模型

对于单回路三相线路而言，有如图1线路简图。

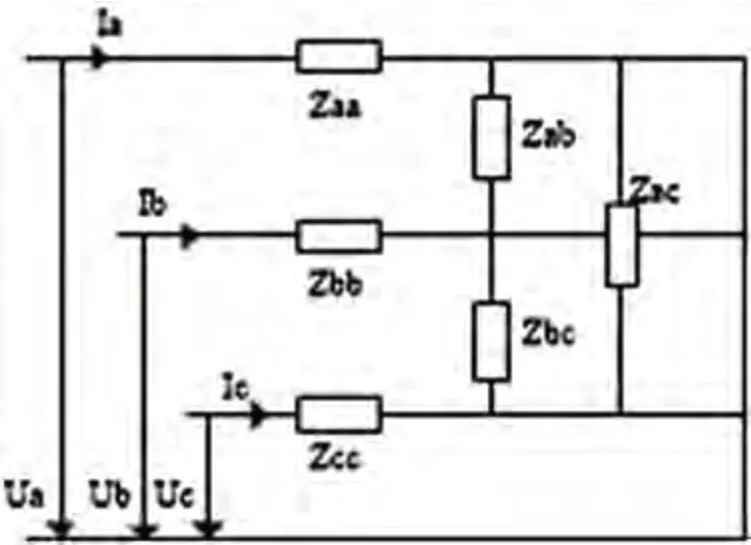
图1 单回路三相线路

此时有

式中：UP=[UaUbUc]T，IP=[IaIbIc]T

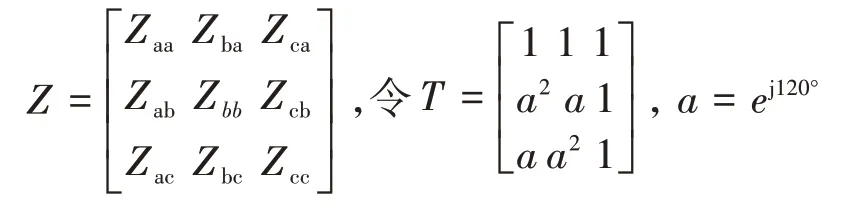
则通过TU120=ZTI120，得到序分量。若线路的对称性好，则耦合阻抗为零[3]。此时有：正序阻抗Z1=Zs－Zm；负序阻抗Z2=Zs－Zm；零序阻抗Z0=Zs+2Zm。至此，线路参数通过解耦得到序分量，即转变为求解线路自阻抗Zs及线路互阻抗Zm。

1.1 自阻抗及互阻抗计算

采用“单导线-大地”计算其自阻抗互阻抗为：

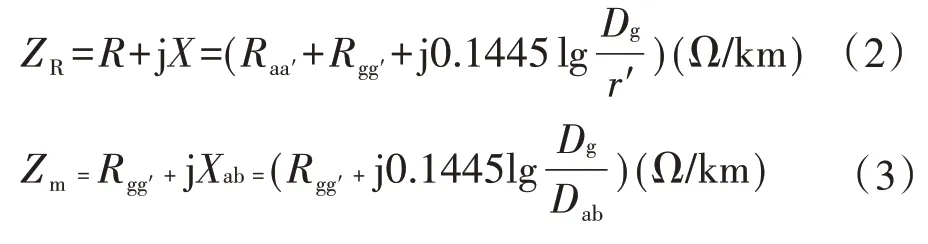
式中：Dg为等值深度

ρ为土壤电导率；f为频率；rˊ为导线内部电感下的 导 线 等 值 半 径 。Rgg′=π2×10-4×f=9.869×10-4×f。Raa′=ρl/S。

1.2 序阻抗计算

若线路完全换位，此时序参数计算如下[5]。

1）正序阻抗

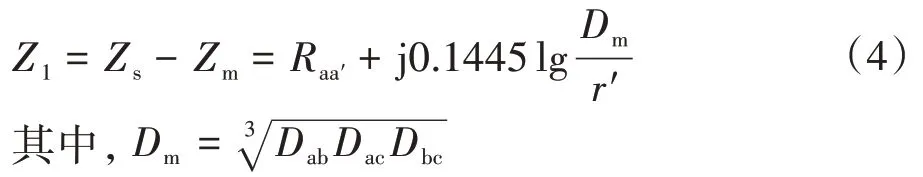
2）负序阻抗

3）零序阻抗

若两回输电线采用相同的结构及参数即ZI0=ZII0=Z0，则双回路的零序阻抗为

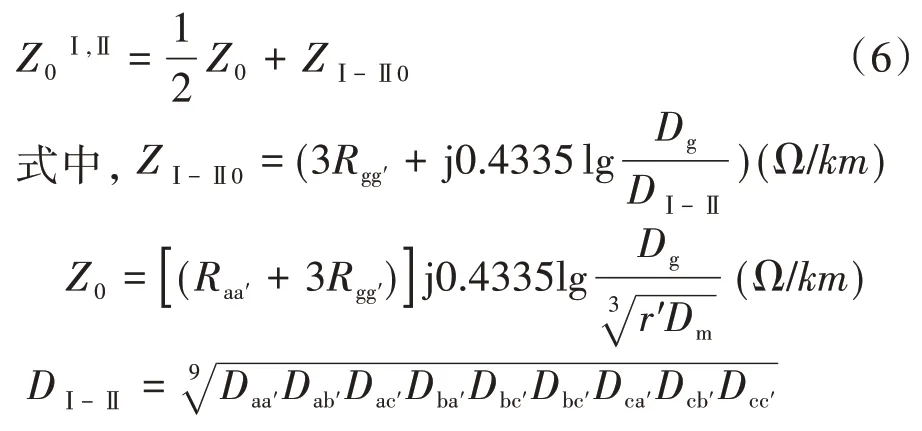
2 同塔双回500 kV输电线模型设计基本原理

同塔双回输电线路各线的自感及线间互感是通过线路通电后产生的空间磁场耦合来得到的[6]。六线之间均有耦合的作用，因此模型设计最主要思想即分别模拟各线之间的互感，当各线之间的互感完全被模拟时，其对外的特性（正序、负序和零序阻抗）也就和实际线路的对外特性一致，同时也能很好的模拟实际线路局部的特征。

2.1 两线路互感

图2表示对于无限长架空多回任意距离为d的两相线路1和线路2之间的互感原理图。

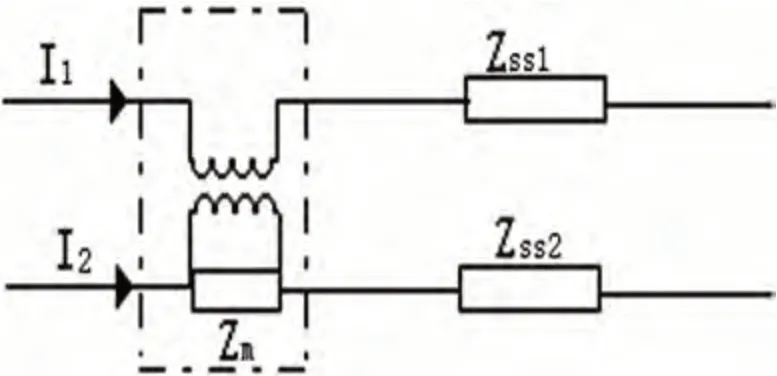
图2 两线路间互感

当线路1 通入电流后，由毕奥-萨伐尔定律可解释电流元在空间任意点P 处所激发的磁场，当两个载流线路的电流可以互相提供磁通时，那么它们之间存在互感耦合，若将两相线路之间产生的互感，放在某一线上拟作此线路的阻抗，因此有如下关系式。

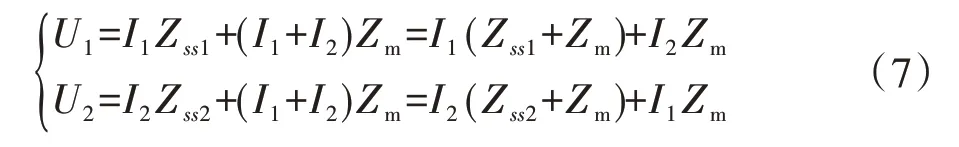
2.2 两回路互感

图3表示此模型下两回路间的互感原理图。

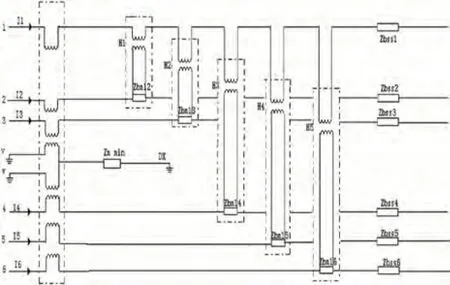
图3 两回路间互感

将线路所有的互感根据卡松公式求取出来，取其最小值作为所有相线之间的公共的最小互阻抗，命名为Zmmin。此时线路其他互感均为原先值与Zmmin之间的差值且为正值定义为补偿互阻抗Zbmlk（k=2，3……6）。同时考虑实际中同塔双回路均采用双地线的情况，流经Zmmin的电流为双回六线的电流之和。因此将Zmmin作为地线的阻抗。

由图3可得电压表达式

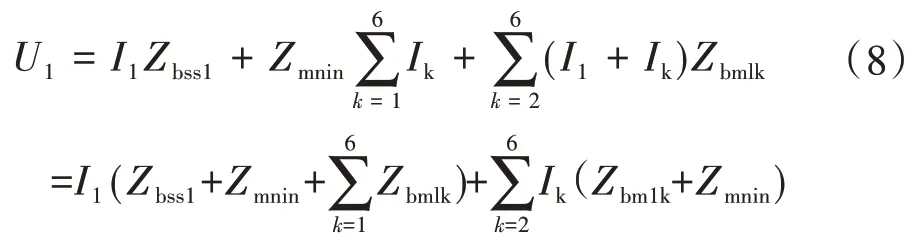
此时回路1的A相自阻抗为

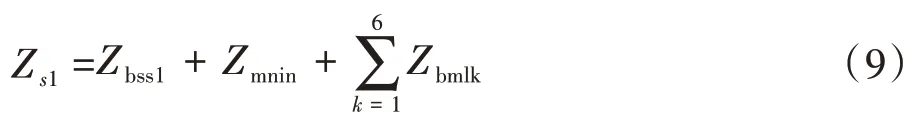
A相与其他线路的互阻抗为

3 模型设计实现与实验校验

3.1 同塔双回实际线路仿真模型

采用500 kV 龙滩—沙塘同塔双回输电线路为线路原型。线路全长2×262 km，全线共塔，基塔561座，逆相序布置。双地线型号为GJ-80。导线采用垂直排列方式，第一二回导线分裂间距450 mm，型号为4×LGJ-400/50 及 4×LGJ-400/35。建立基于 ATP-EMTP 的龙滩—沙塘双回路导线仿真模型。正序及零序阻抗参数结果分别如表1、表2所示。

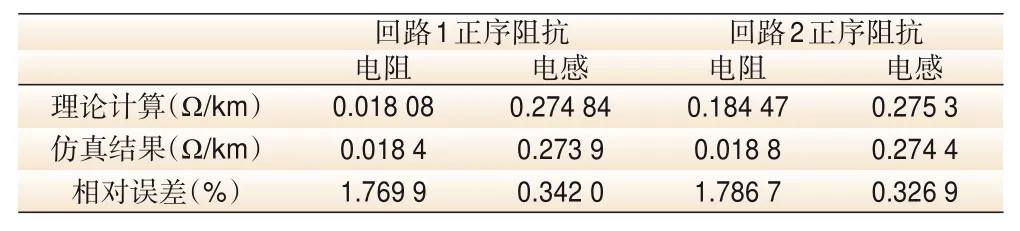
表1 正序阻抗参数结果

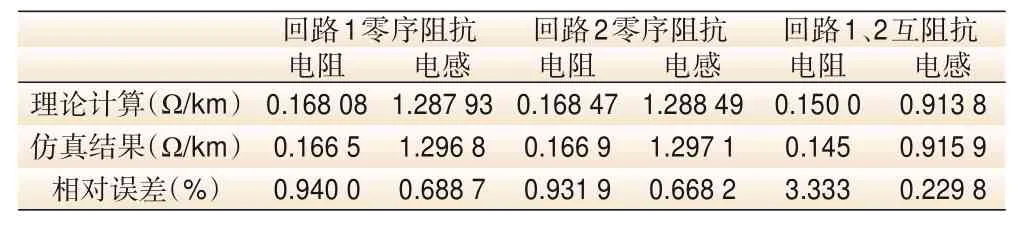
表2 零序阻抗参数结果

由表1、表2可知，该仿真模型参数与实际理论计算的结果相对误差在5%以内，仿真模型建立合理，因此可用以与设计模型作动态物理模拟对比。

3.2 同塔双回输电线路设计模型

以龙滩—沙塘同塔双回六相线两回地线为例，线路全长262 km。取互感最小值Zmmin=Zm16=0.05+j0.2853（Ω/km）。计算所有相线的补偿自阻抗Zbssk（Ω/km）及补偿互阻抗Zbmik（Ω/km）以建立设计模型。

3.3 模型校验

3.3.1 正常运行

表3 表示当系统正常运行时，实际线路的序阻抗参数与设计模型的序阻抗参数误差计算值。

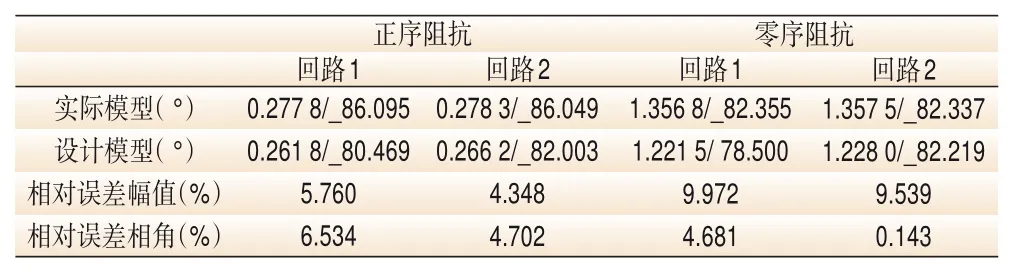
表3 正常运行参数

从误差计算表格来看，正序以及零序阻抗相对误差均在10%以内。误差控制在允许范围之内，则模型设计合理。

3.3.2 故障模拟

分别模拟单相接地、两相接地、三相接地故障及工频过电压，以验证文中设计的模型合理性。

1）单相接地故障

0.01 s 回路 I 发生 A 相单相接地故障，在 0.03 s 保护动作跳开故障，则实际模型及设计模型的电压电流变化情况如图4-图7所示。

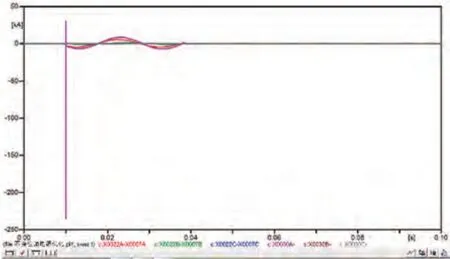
图4 线路I-A单相接地实际模型电流

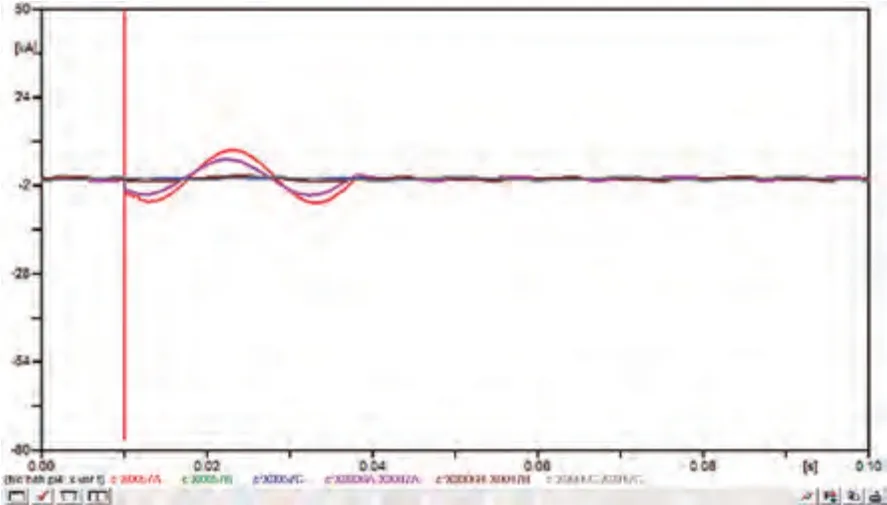
图5 线路I-A单相接地设计模型电流

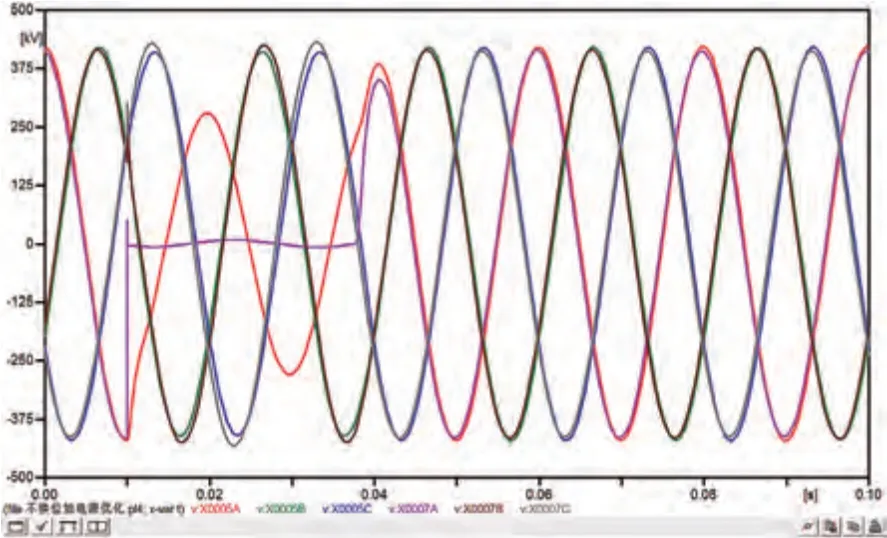
图6 线路I-A单相接地实际模型电压

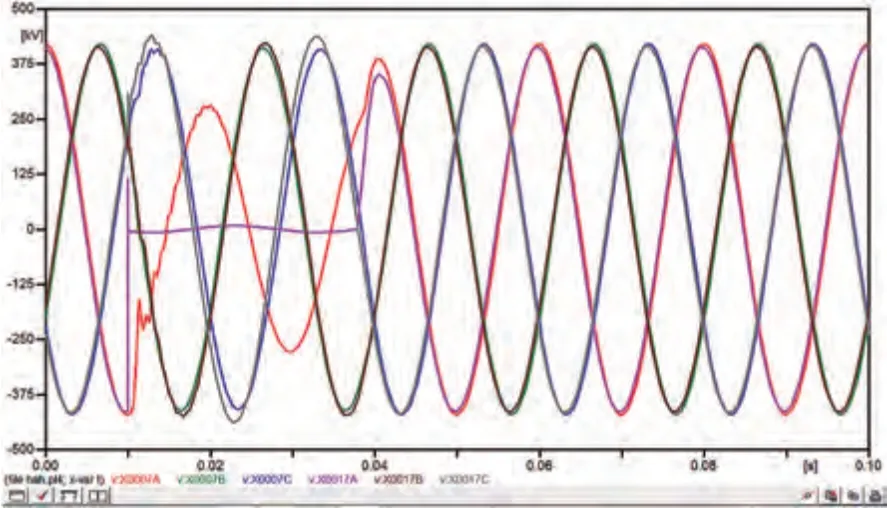
图7 线路I-A单相接地设计模型电压

2）两相接地故障

0.01 s 回路 I 发生 AB 两相接地故障，在 0.03 s 保护动作跳开故障，则实际模型及设计模型的电压电流变化情况如图8-图11所示。

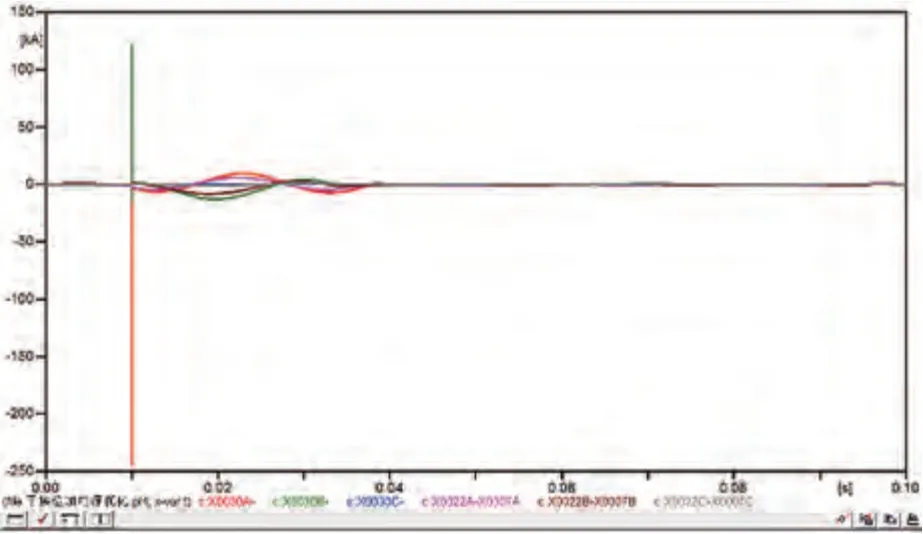
图8 线路I-AB两相接地实际模型电流

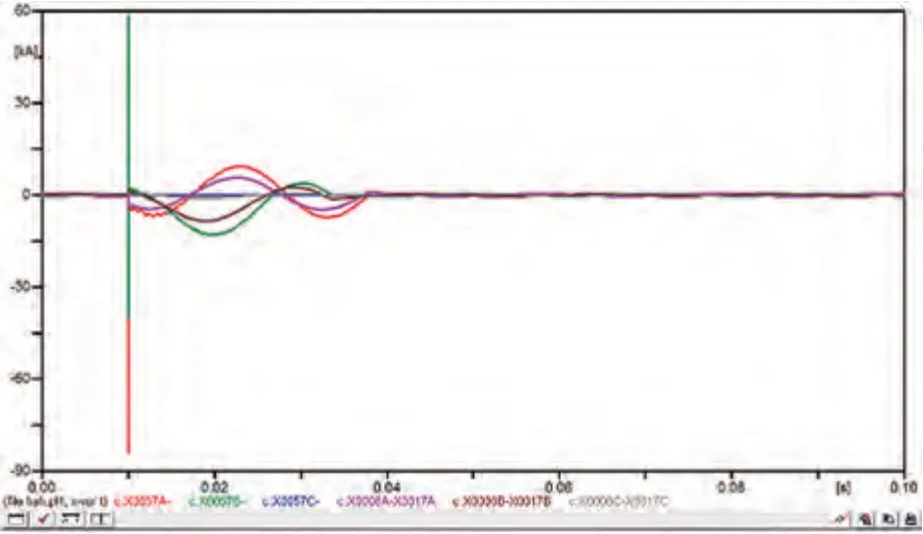
图9 线路I-AB两相接地设计模型电流

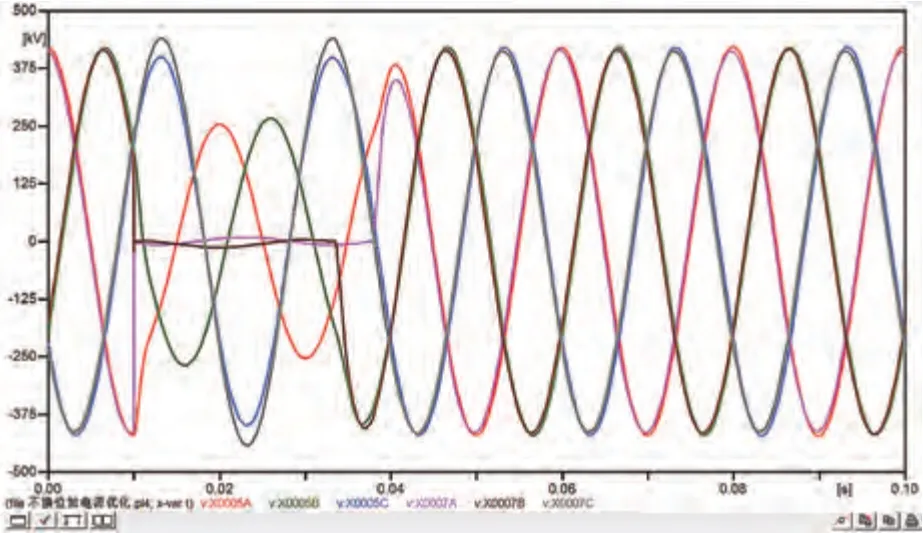
图10 线路I-AB两相接地实际模型电压

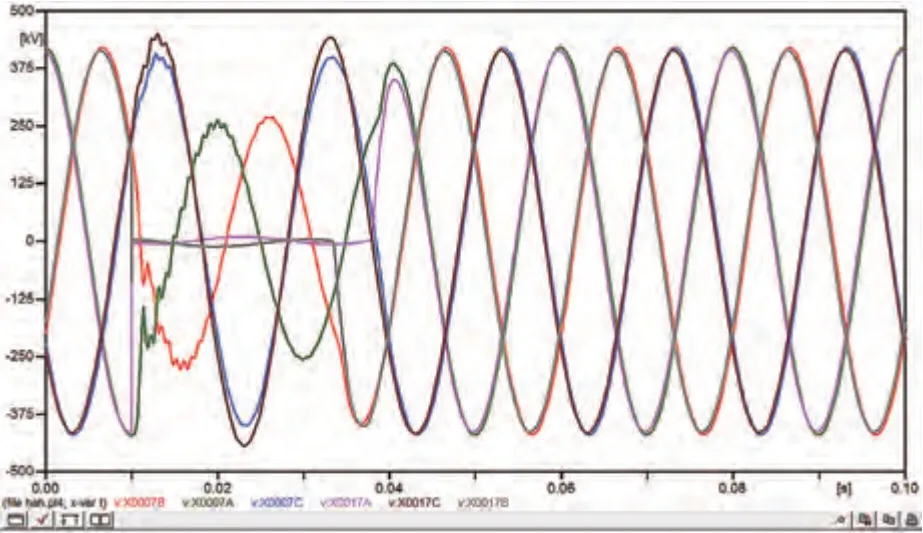
图11 线路I-AB两相接地设计模型电压

3）三相接地故障

0.01 s 回路I发生三相接地故障，在0.03 s 保护动作跳开故障，则实际模型及设计模型的电压电流变化情况如图12-图15所示。

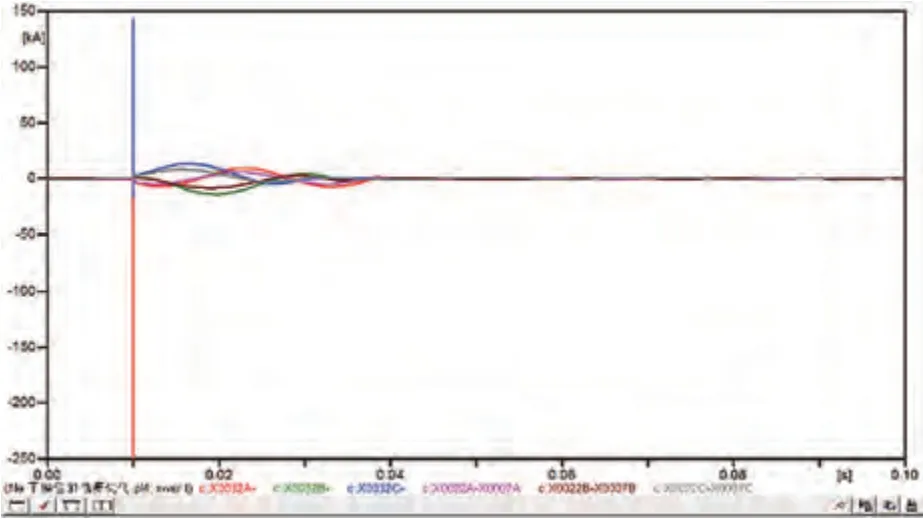
图12 线路I-ABC三相接地实际模型电流

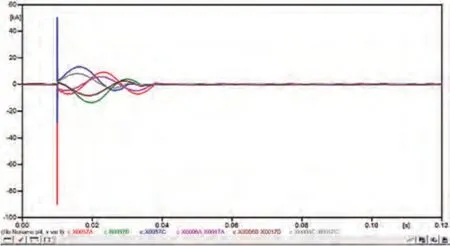
图13 线路I-ABC三相接地设计模型电流

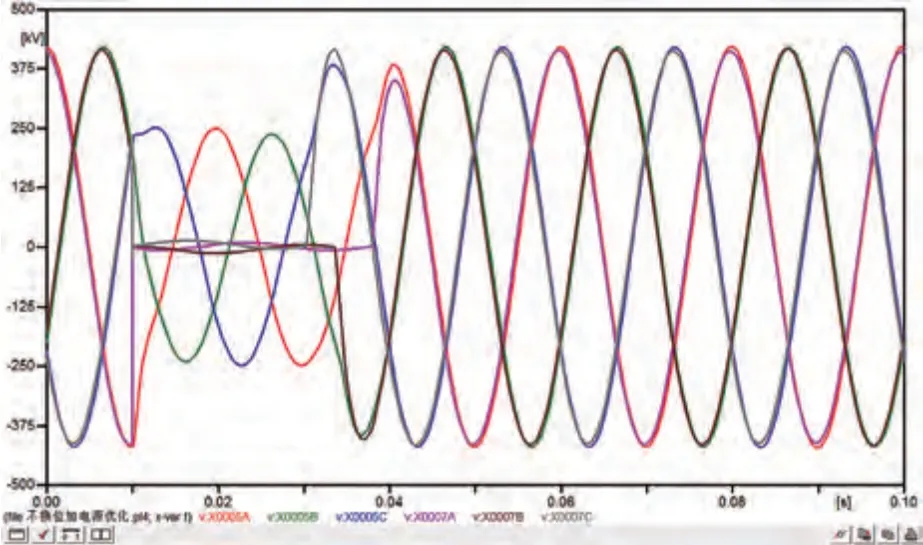
图14 线路I-ABC三相接地实际模型电压

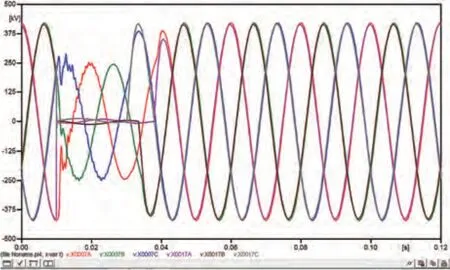
图15 线路I-ABC三相接地设计模型电压

4）工频过电压

0.01 s 时刻线路空载合闸，模拟空载长输电线路工频过电压，则实际模型及设计模型的首末端电压变化情况如图16、图17所示。

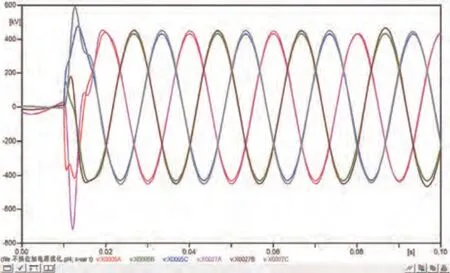
图16 工频过电压实际模型I回线路首末端电压

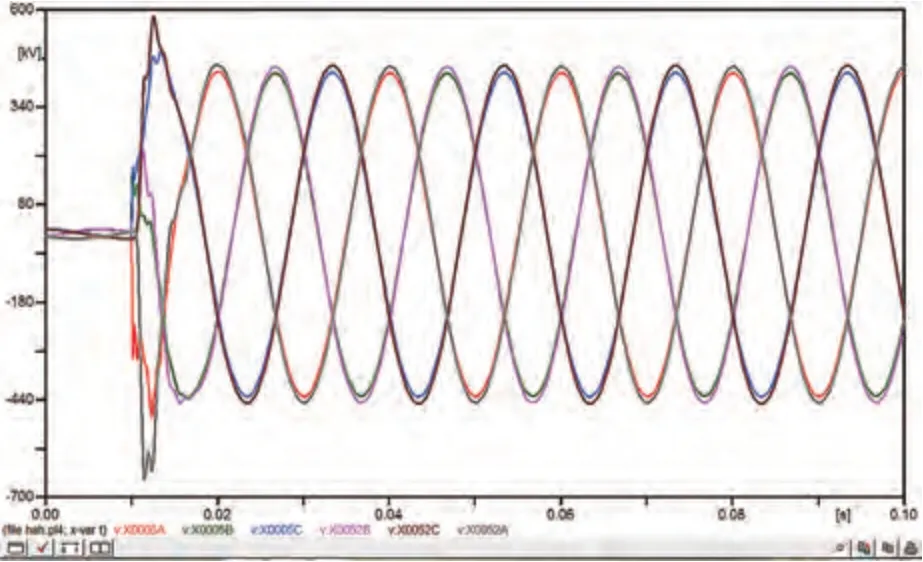
图17 工频过电压设计模型I回线路首末端电压

由模拟回路I 的单相接地，两相接地及三相接地故障以及工频过电压实验结果对比可以看出，该设计模型的对外特性与实际模型相符合，进一步论证模型设计的可行性，因此可以用于研制实际的物理模型，为相关继电保护装置的研制提供理论基础。

4 结语

文中首先对同塔多回输电线路的数学模型理论进行分析，并设计了一种以π型模型为基础的，可以全面反映线间互感的同塔多回输电线路参数模型。然后分别建立了以龙滩—沙塘线路的实际仿真模型以及设计模型。最后通过相关参数计算及接地故障和工频过电压实验，说明了所设计的模型可以真实反映实际线路的物理特性，对外特性与实际模型相符合，论证了模型设计的可行性及合理性，可为相关继电保护及控制原理的研究和装置的研制提供理论基础。