基于改进复合序网络的混压部分同塔双回线跨电压故障分析
汤旻安 ,逯 航
(1.兰州交通大学新能源与动力工程学院,兰州 730070;2.兰州交通大学自动化与电气工程学院,兰州 730070)
同塔线路的架设在提高供电能力的同时降低了线路建设成本,也节约了线路通道用地,是电网发展的必然趋势[1-3]。同塔双回线路由于其结构的复杂性,故障类型相较于单回线更多。同塔双回线路接地故障63种、不接地故障57种、单线故障22种、跨线故障98种[4]。尤其对于混压部分同塔双回输电线路,不同电压等级两回线路之间发生的短路故障作为其特有的故障类型。两种不同电压等级的线路通过短路点相互注入功率,加之混压部分同塔线路的结构更为复杂,双回线同塔部分存在零序互感[5-6],使得混压部分同塔双回输电线路的故障电流的组成更加复杂,故障特征分析也越发困难[7-8]。
同塔双回线路故障的研究重点大多在于相同电压等级双回线路的各类型故障的分析[9-11],而对混压同塔双回线路跨电压故障分析的研究较少[12-13]。针对同一电压等级下的各类型故障,目前常用的方法为六序分量法[14-15],该方法只能局限于相同电压等级系统两回路参数对称的情况,而当不同电压等级系统参数不对称时并不适用[16]。对于混压部分同塔双回线路跨电压故障,文献[17]利用复故障分析法[18]建立等效的正、负和零序网络,再利用移相变压器构成复合序网络,对故障电流进行了分析计算。
本文基于文献[19]提出的改进复合序网法,分析混压部分同塔双回线路的跨电压等级故障特征,在建立并简化混压部分同塔双回线路的各序参数的基础上,建立线路各序等效模型,再结合各类型故障的边界条件,画出各类型故障的改进复合序网络,由改进复合序网络求解出故障点的电压、电流等故障特征。通过PSCAD软件建立220 kV/110 kV混压部分同塔双回输电线路模型,对各类型的故障进行仿真,验证了该方法在混压部分同塔双回输电线路应用的准确性。
1 混压部分同塔双回输电线路各序等效模型求解
混压部分同塔双回线模型如图1所示,其中双回线分别用LⅠ、LⅡ表示(或简记为Ⅰ、Ⅱ),LⅠ的三相参数分别用A、B、C表示;LⅡ的三相参数分别用a、b、c表示;对于各序参数,分别用1、2、0表示正序、负序、零序;m、n分别表示系统送端与受端;KⅠ、KⅡ分别为线路Ⅰ和线路Ⅱ的故障点;α为同塔部分占线路总长度比例;β为同塔部分起点到故障点的距离占同塔部分总长度比例;分别为 LⅠ、LⅡ的送端与受端电源电动势。

图1 混压部分同塔双回线路故障示意Fig.1 Schematic of mixed-voltage double-circuit lines partially on the same tower under fault
对于双回线路,正序、负序分量线间互感较小,可忽略不计,本文假定线路正、负序参数完全相同。图2(a)为该双回线路正序参数模型。对于该双回线路正序参数,利用阻抗等效变换可以得到正序等效模型如图2(b)所示,其中ZLⅠ,e,1、ZLⅡ,e,1分别为LⅠ、LⅡ的正序等效阻抗。

图2 混压部分同塔双回线路正序等效参数模型Fig.2 Positive-sequence equivalent parameter model of mixed-voltage double-circuit lines partially on the same tower
图2中的ZLⅠ,m,1、ZLⅡ,m,1、ZLⅠ,n,1、ZLⅡ,n,1分别为LⅠ、LⅡ的送端电源正序阻抗和受端电源正序阻抗。由图2可得

式中:ZLⅠ,1、ZLⅡ,1分别为 LⅠ、LⅡ的输电线路正序阻抗;ZLⅠ,a,1、ZLⅠ,b,1分别为 LⅠ从m、n端到故障点的正序阻抗;ZLⅡ,a,1、ZLⅡ,b,1分别为 LⅡ从m、n端到故障点的正序阻抗。
对于正序网络,还需要分析电源的等效电动势。不对称故障使得故障点三相对地电压与三相流出电流均不对称,而这时发电机的电动势仍为三相对称的正序电动势,因此需要在混压部分同塔双回线路正序网络中讨论其等效正序电动势。对于等效正序电动势,只需要利用前面的正序参数模型,采用同样思路即可对正序电动势进行等效变换,得到 LⅠ、LⅡ等效正序电动势分别为。
对于负序网络,由于其参数和简化过程与正序完全相同,因此仅给出等效结果如图3所示,其中ZLⅠ,e,2、ZLⅡ,e,2分别为LⅠ、LⅡ的负序等效阻抗。

图3 混压部分同塔双回线路负序等效参数模型Fig.3 Negative-sequence equivalent parameter model of mixed-voltage double-circuit lines partially on the same tower
对于零序网络,在其等效过程中必须考虑两回线路的同塔部分之间的零序互感,而非同塔部分的零序互感较小,故将其忽略,得到如图4(a)所示的混压部分同塔双回线路零序参数模型。对于两回线路同塔部分之间零序互感,使用经典的零序解耦法进行解耦等效,再利用阻抗的等效变换可以将零序参数模型等效为如图4(b)所示的网络,其中ZLⅠ,e,0、ZLⅡ,e,0分别为 LⅠ、LⅡ零序等效阻抗,Zh,e,0为同塔部分的零序等效互阻抗。

图4 混压部分同塔双回线路零序等效参数模型Fig.4 Zero-sequence equivalent parameter model of mixed-voltage double-circuit lines partially on the same tower
图4中的ZLⅠ,m,0、ZLⅡ,m,0分别为 LⅠ、LⅡ的送端电源零序阻抗;ZLⅠ,n,0、ZLⅡ,n,0分别为 LⅠ、LⅡ的受端电源零序阻抗;Zh,0为同塔部分的零序互阻抗。由图4可得
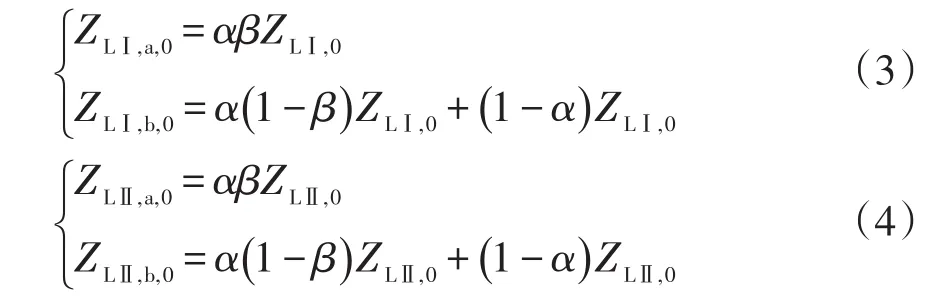
式中:ZLⅠ,0、ZLⅡ,0分别为LⅠ、LⅡ的输电线路零序阻抗;ZLⅠ,a,0、ZLⅠ,b,0分别为 LⅠ从m、n端到故障点的零序阻抗;ZLⅡ,a,0、ZLⅡ,b,0分别为 LⅡ从m、n端到故障点的零序阻抗
至此,混压部分同塔双回线路的正、负、零序等效模型已经全部得出。对于不同类型的故障,依据其不同的故障边界条件,利用已得出的各序等效参数模型,将复合序网络的网络参数、结构等内容进行修改,得到改进的复合序网络,在此基础上对各类型故障进行分析。
2 混压部分同塔双回输电线路故障分析
2.1 跨电压接地故障
2.1.1 单相跨单相接地故障
以LⅠ的A相跨LⅡ的a相接地故障为例(用A-a-g来表示),线路Ⅰ、Ⅱ的短路点边界条件为

将式(5)分解为特殊相(线路Ⅰ的A相与线路Ⅱ的a相)的对称分量,即

根据式(6)中的特殊相电压电流对称分量之间的关系,再结合前文求解的各序参数等效模型,可以得出单相跨单相接地故障的改进复合序网络如图5所示。

图5 A-a-g故障的改进复合序网络Fig.5 Improved composite-sequence network under fault A-a-g
根据图5中复合序网络可以得到特殊相(A相与a相)正序电流之间的关系为
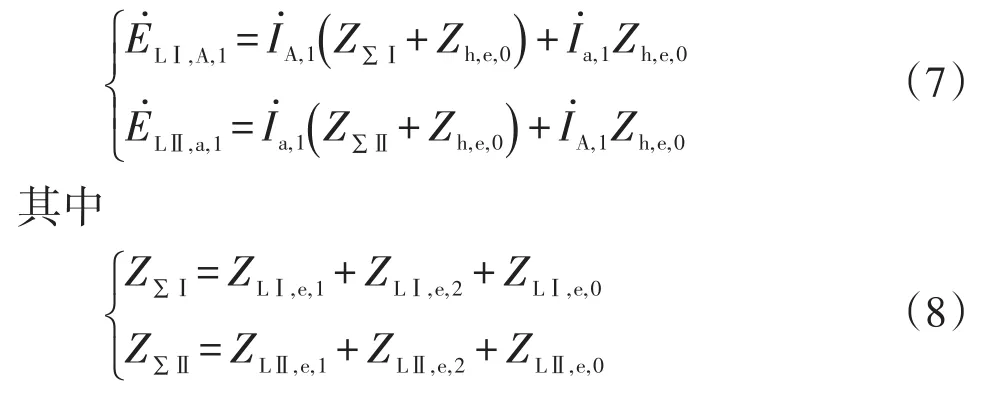
根据式(7)中序电流关系及式(6)中特殊相的电流各序分量关系,可以得到单相跨单相接地故障相(A相与a相)各序电流及相电流的表达式分别为
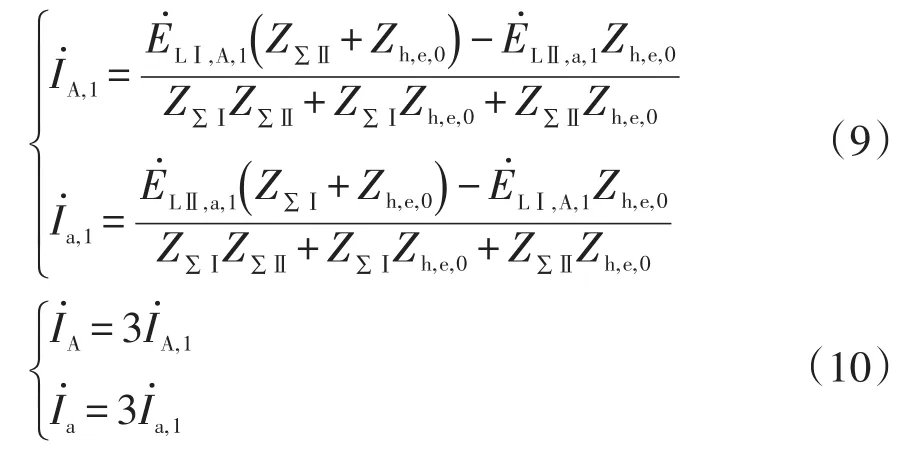
2.1.2 单相跨两相接地故障
以LⅠ的A相跨LⅡ的b、c相接地故障为例(用A-bc-g来表示),篇幅所限,此处仅给出线路Ⅰ、Ⅱ的短路点边界条件分解为特殊相(线路Ⅰ的A相与线路Ⅱ的a相)的对称分量,即

根据式(11)中的特殊相电压、电流的对称分量之间的关系,可以得出单相跨两相接地故障的改进复合序网络如图6所示。

图6 A-bc-g故障的改进复合序网络Fig.6 Improved composite-sequence network under fault A-bc-g
根据图6中复合序网络,可以得到特殊相(A相与a相)零序电流之间的关系为

因此,单相跨两相接地故障中的故障相(A相与b、c相)相电流及特殊相(A相与a相)各序电流的表达式分别为
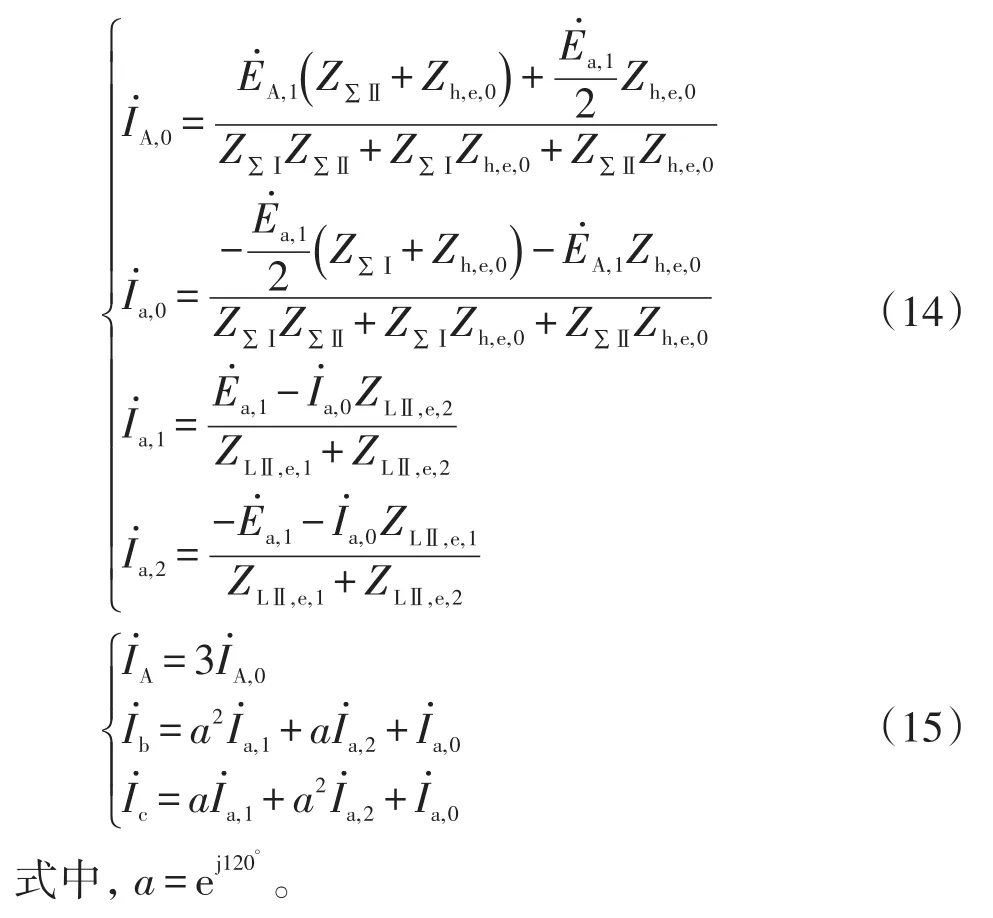
2.1.3 单相跨三相接地故障
以LⅠ的A相跨LⅡ的a、b、c相接地故障为例(用A-abc-g来表示),边界条件分析方法与前面类似,故不再赘述,此处仅给出单相跨三相接地故障的改进复合序网络如图7所示。
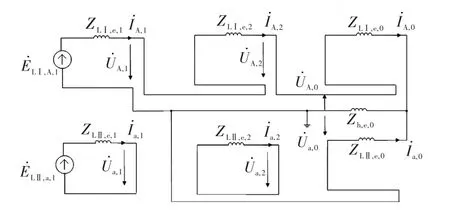
图7 A-abc-g故障的改进复合序网络Fig.7 Improved composite-sequence network under fault A-abc-g
根据图7中复合序网络,可以得到特殊相(A相与a相)零序电流之间的关系为

因此,单相跨三相接地故障特殊相(A相与a相)各序电流及故障相(A相与a、b、c相)相电流的表达式分别为


2.1.4 两相跨两相接地故障
以LⅠ的B、C相跨LⅡ的b、c相接地故障为例(用BC-bc-g来表示),两相跨两相接地故障的改进复合序网络如图8所示。
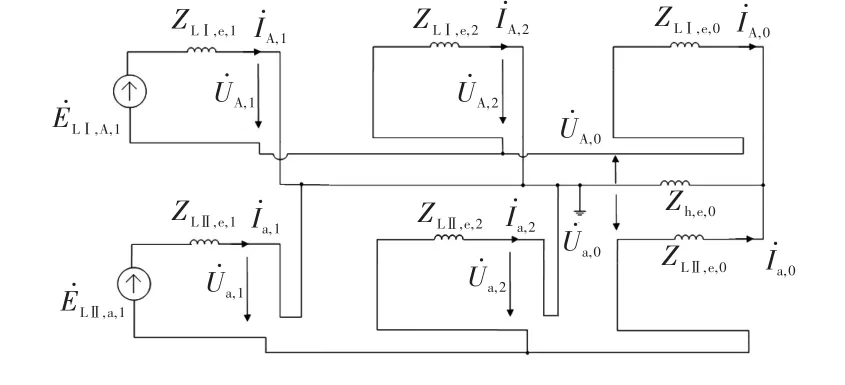
图8 BC-bc-g故障的改进复合序网络Fig.8 Improved composite-sequence network under fault BC-bc-g
因此,两相跨两相接地故障下的特殊相(A相与a相)的各序电流及故障相(B、C相与b、c相)相电流的表达式分别为

2.1.5 两相跨三相接地故障
以 LⅠ的B、C相跨 LⅡ的a、b、c相接地故障为例(用BC-abc-g来表示),两相跨三相接地故障的改进复合序网络如图9所示。

图9 BC-abc-g故障的改进复合序网络Fig.9 Improved composite-sequence network under fault BC-abc-g
因此,两相跨两相接地特殊相(A相与a相)的各序电流及故障相(B、C相与a、b、c相)相电流的表达式为

2.2 跨电压不接地故障
2.2.1 单相跨单相不接地故障
以LⅠ的A相跨LⅡ的a相不接地故障为例(用A-a表示),单相跨单相不接地故障改进复合序网络如图10所示,为故障点对地电压。

图10 A-a故障的改进复合序网络Fig.10 Improved composite-sequence network under fault A-a
单相跨单相不接地故障中故障相(A相、a相)各序电流及相电流的表达式分别为

2.2.2 单相跨两相不接地故障
以LⅠ的A相跨LⅡ的b、c相不接地故障为例(用A-bc表示),单相跨两相不接地故障改进复合序网络如图11所示。

图11 A-bc故障的改进复合序网络Fig.11 Improved composite-sequence network under fault A-bc
因此,单相跨两相不接地故障中的特殊相(A相与a相)各序电流及故障相(A相与b、c相)相电流的表达式分别为
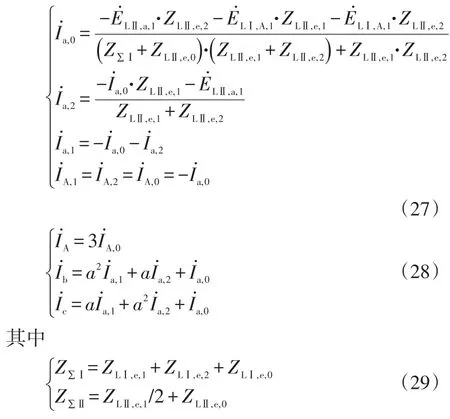
2.2.3 单相跨三相不接地故障
以LⅠ的A相跨LⅡ的a、b、c相不接地故障为例(用A-abc来表示),单相跨三相不接地故障改进复合序网络如图12所示。
因此,单相跨三相不接地故障中的特殊相(A相与a相)各序电流及故障相(A相与a、b、c相)相电流的表达式分别为

图12 A-abc故障的改进复合序网络Fig.12 Improved composite-sequence network under fault A-abc

2.2.4 两相跨两相不接地故障
以LⅠ的B、C相跨LⅡ的b、c相不接地故障为例(用BC-bc表示),两相跨两相不接地故障改进复合序网络如图13所示。

图13 BC-bc故障的改进复合序网络Fig.13 Improved composite-sequence network under fault BC-bc
因此,两相跨两相不接地故障下的特殊相(A相与a相)各序电流及故障相(B、C相与b、c相)相电流的表达式分别为


2.2.5 两相跨三相不接地故障
以 LⅠ的B、C相跨 LⅡ的a、b、c相不接地故障为例(BC-abc表示),两相跨三相不接地故障改进复合序网络如图14所示。
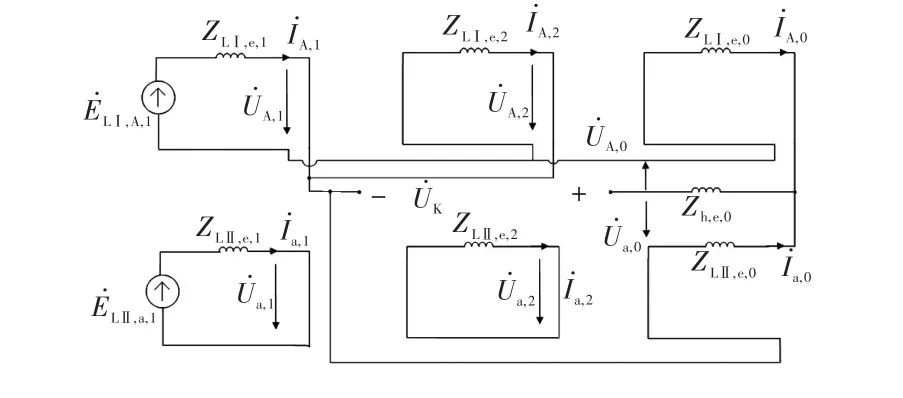
图14 BC-abc故障的改进复合序网络Fig.14 Improved composite-sequence network under fault BC-abc
因此,两相跨三相不接地故障下特殊相(A相与a相)各序电流及故障相(B、C相与a、b、c相)相电流的表达式分别为

2.3 小结
(1)对于混压部分同塔双回线的三相跨三相故障来说,三相故障电流依旧对称,因此没有零序电流的产生,也就没有两线之间故障电流耦合,可视作两回相互独立的线路发生三相故障,可用传统的故障分析方法进行分析,故本文不再进行讨论。
(2)根据分析对象的不同,调整同塔部分占线路总长度的比例α与同塔部分的起点到故障点的距离占同塔部分总长度的比例β,可以将该方法应用于不同同塔比例的混压部分同塔双回线路任一故障点处发生的各类型跨电压故障。
3 仿真验证
PSCAD软件中搭建如图1所示的输电线路,其中,220 kV电源的正序阻抗为j70 Ω,零序阻抗为j93 Ω;220 kV线路的正序单位阻抗为0.041 5+j0.323 3 Ω/km,零序单位阻抗为0.2673+j1.271 4 Ω/km;110 kV电源的正序阻抗为j50 Ω,零序阻抗为j80 Ω;110 kV线路的正序单位阻抗0.118 1+j0.715 2 Ω/km,零序单位阻抗0.606 2+j1.034 5 Ω/km;两回线路的同塔部分线间零序耦合电感的单位阻抗为0.197 2+j0.567 9 Ω/km,两回线路的总长度均为150 km;两回线路的电源初相角设定均为受端电源滞后送端电源15°。为验证该方法对于混压部分同塔双回线路的广泛适用性,考虑两种不同的同塔比例下不同故障位置的混压部分同塔双回线路发生的跨电压故障进行仿真验证。
3.1 跨电压接地故障的仿真验证
假设α=2/3与β=1/2,对混压部分同塔双回线路的跨电压故障进行仿真验证。表1和表2分别为跨电压接地故障下的故障电流有效值与相位角的仿真与计算结果的误差分析,其中绝对误差为计算结果与仿真结果之差的绝对值,相对误差为绝对误差与计算结果的比值(用百分数表示)。
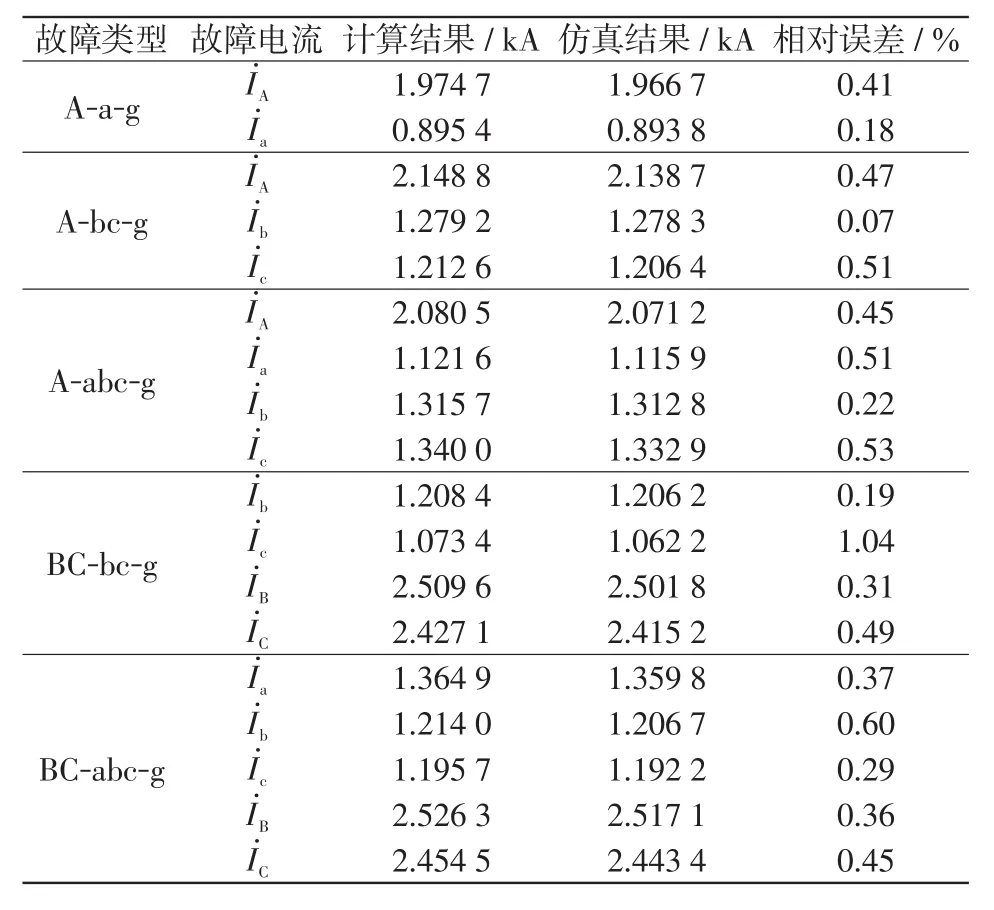
表1 接地故障下故障电流有效值对比Tab.1 Comparison of RMS current under earthed fault

表2 接地故障下故障电流相位角对比Tab.2 Comparison of current phase angle under earthed fault
从表1和表2中可以看出,混压部分同塔双回线路故障电流计算方法对于跨电压接地故障的计算误差很小,结果较为精确。
3.2 跨电压不接地故障的仿真验证
表3和表4分别为不接地故障下故障电流有效值与相位角的仿真与计算结果的对比。
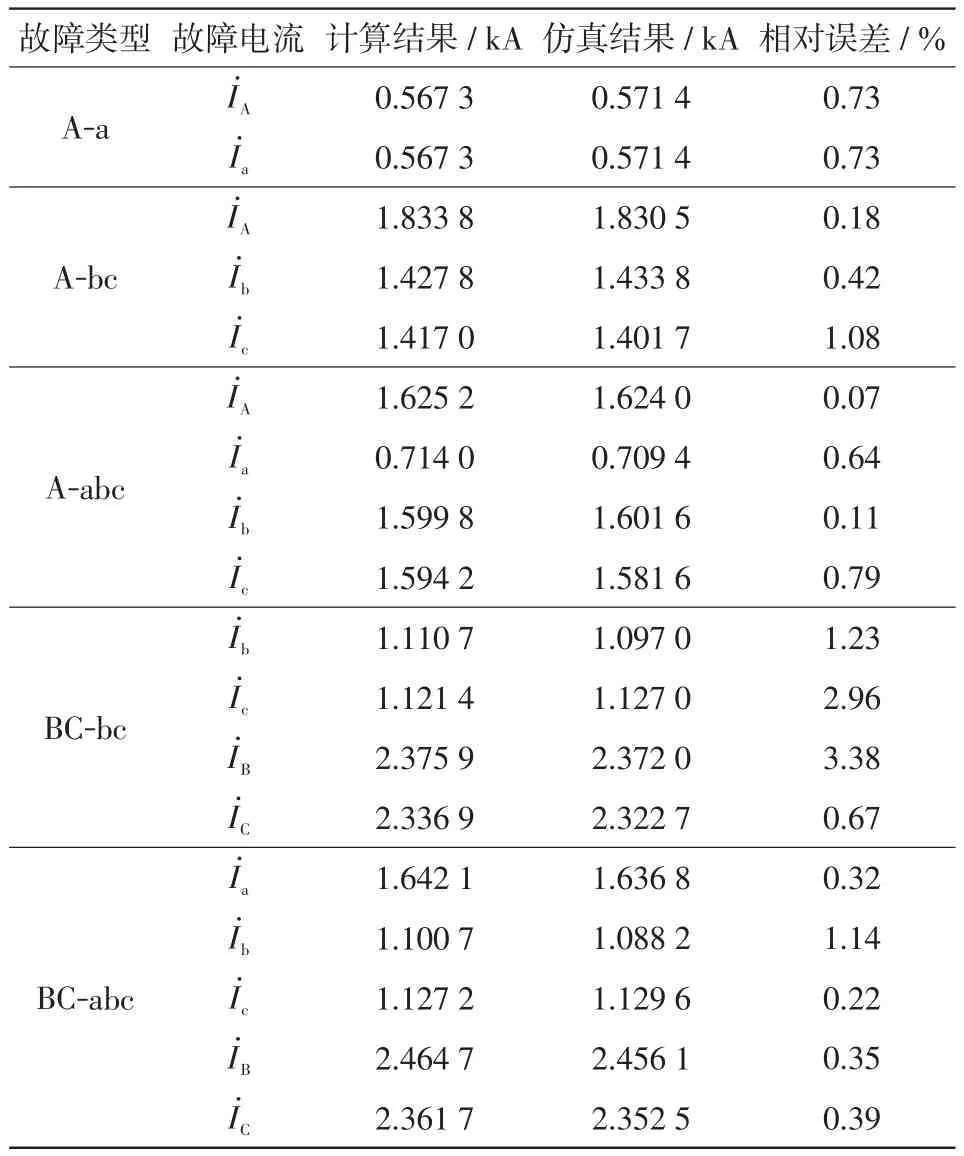
表3 不接地故障下故障电流有效值对比Tab.3 Comparison of RMS current under unearthed fault
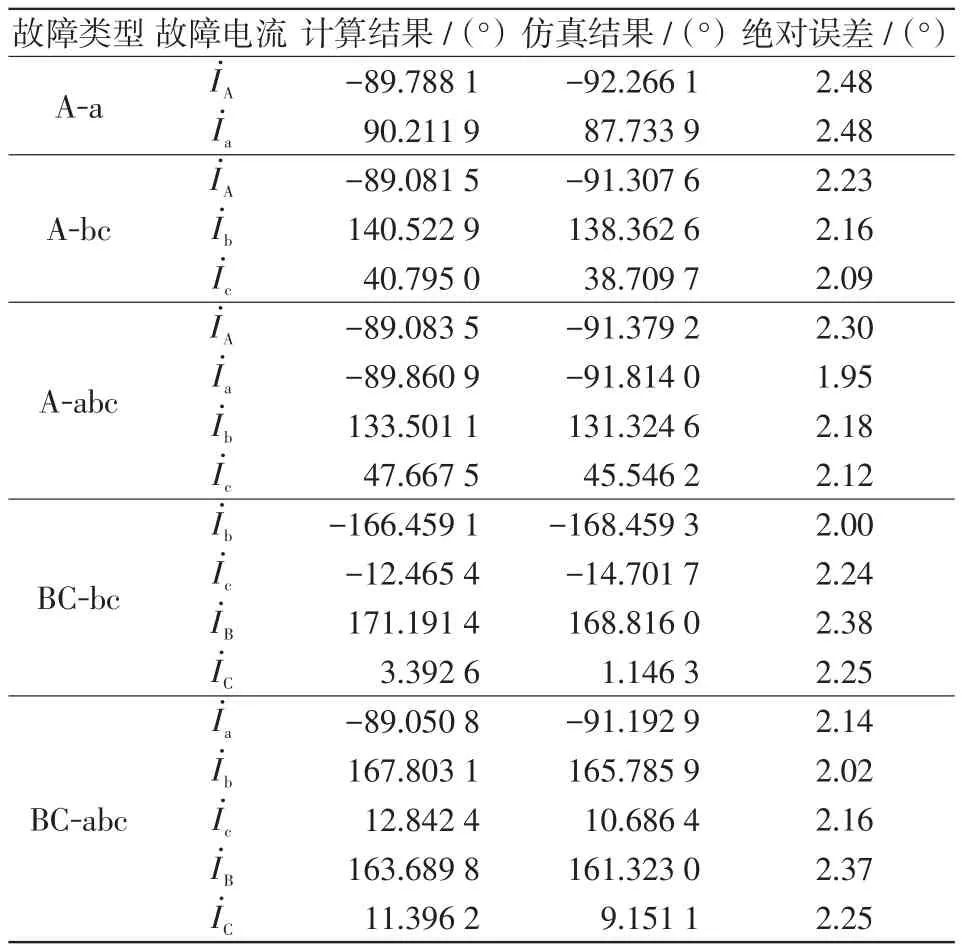
表4 不接地故障下故障电流相位角对比Tab.4 Comparison of current phase angle under unearthed fault
从表3和表4可以看出,该故障电流分析方法对于跨电压不接地故障的计算误差很小,同样适用。
3.3 不同比例参数下的跨电压接地故障仿真验证
假设α=4/5与β=3/4,对混压部分同塔双回线路的跨压故障进行仿真验证。
表5和表6分别为该线路比例参数下的接地故障的故障电流有效值与故障电流相位角的仿真与计算结果的误差分析。

表5 不同同塔比例线路的故障电流有效值对比Tab.5 Comparison of RMS current under fault among lines with different proportions of lines on the same tower

表6 不同同塔比例线路的故障电流相位角对比Tab.6 Comparison of current phase angle under fault among lines with different proportions of lines on the same tower
从表5和表6可以看出,计算结果与仿真结果之间误差很小,表明该方法对于混压部分同塔双回输电线路具有广泛适用性。
由于篇幅所限,本文只给出α分别为2/3和4/5时的仿真验证。应当说明,当α=1时,即完全同塔的情况下,该方法也同样适合,只需调整相应比例参数。
对比各类型故障下的误差结果可以看出,故障电流有效值的计算结果与仿真结果的相对误差基本上在1%以内,故障电流相位角的计算与仿真结果的绝对误差基本上在2.5°以内,均属于高精度计算下的微小范围误差。
4 结论
本文基于改进的复合序网络提出了混压部分同塔双回输电线路故障特征的计算方法,并详细分析混压部分同塔双回输电线路的等效参数模型,以及10种不同电压等级之间故障的故障电流分析方法,得出如下结论。
(1)对于任意同塔比例的部分混压同塔双回线路,在线路任一点处出现两线之间短路故障,只需要确定该线路同塔部分占线路总长度的比例及同塔部分起点到故障点的距离占同塔部分总长度比例,即可应用本文中等效参数模型进行故障电流计算。
(2)对于混压部分同塔双回线路来说,由于不同电压等级线路之间互感的存在,任意类型跨电压故障中,一回线路的故障电流都与另一条线路的电气参数密切相关。对于相应继电保护装置来说,不能再使用单回输电线路电气参数作为判断故障的依据,而需要考虑同塔的另一回线路电气参数。
(3)混压部分同塔双回输电线路与常规的输电线路相比,受到同塔部分不同电压等级两条线路之间互感影响,不接地故障也产生零序电流。而这对于使用零序电压和电流作为接地故障判定依据的常规继电保护装置来说,需要针对这一问题进行相应调整,以避免影响继保装置灵敏反应与可靠动作。
本文故障分析方法适用范围广,可应用于同塔双回输电线路的各类型的两线之间短路故障。下一步,可依据本文方法对同塔双回输电线路的继电保护装置的动作原理和动作特性进行研究。

