箱梁与缆索承重桥梁理论2019年度研究进展

白伦华，沈锐利

(西南交通大学 土木工程学院，成都610031)

桥梁结构分析理论的基本问题是桥梁体系、构件中力与变形的求解。传统理论主要涵盖了桥梁结构的空间分析理论、各类梁桥(包括钢桥、混凝土梁桥及组合梁桥)、拱桥及大跨度桥梁(缆索承重桥梁为主)的静力计算理论，桥梁施工过程的时变力学问题也是桥梁结构分析理论研究的一个方面[1]。近年来，随非线性理论的成熟及通用有限元软件的应用推广，桥梁精细化分析理论发展迅速，基于三维实体有限元模型的桥梁抗火、船撞、车撞、落石冲击、波浪冲击及桥梁侧翻等方面的研究丰富了桥梁结构理论的范畴[2]。

1 箱梁分析理论

1.1 波形钢腹板箱梁理论

高性能装配式组合桥梁结构在桥梁工程学科工程开发前沿占据重要一席，波形钢腹板的使用对高性能装配式组合桥梁结构的发展创新具有重要的作用[3]。波形钢腹板箱梁是波形钢腹板应用的主要形式之一，具有材料组合方式、板件连接方式灵活及体外预应力技术协作方便等优点，目前已在滁河大桥、鄄城黄河大桥、桃花峪大桥引桥、头道河大桥等工程中得到应用。近年来，相关研究重点关注了几种新型箱梁(图1)的基本弯、剪、扭及横向受力的分析方法及力学行为。

图1 典型的波形钢腹板箱梁形式(变化底板结构形式)Fig.1 Typical box girders with corrugated steel webs including various structures of lower flange

张紫辰等[4]与王根会等[5]对波形钢腹板组合箱梁(底板为钢板)的剪力滞进行了研究，采用能量变分法推导了该结构形式的剪力滞后控制方程，并采用试验模型与有限元模型进行分析对比。Chen[6]等则通过模型试验、数值模拟及理论推导研究了如图1(a)所示的波形钢腹板箱梁的剪力滞行为，这种箱梁形式充分利用了钢管混凝土的高承载力优势和桁架的减重功能，是一种轻型波形钢腹板箱梁。李运生等[7]考虑了曲率影响、截面剪力滞效应、波形腹板剪切效应、扭转和畸变效应，采用能量变分法推导了波形钢腹板简支曲线结合梁在弯扭效应下的解析解，随后通过固定跨度和截面模型研究了曲线半径和圆心角对弯扭效应的影响，得到了跨中挠度、扭转角等畸变角随圆心角的变化规律。姜瑞娟等[8]提出了基于3个广义位移函数的波形钢腹板组合箱梁剪力滞效应微分方程和基于有限差分法的半解析半数值解法。李丽园等[9]基于能量变分原理推导了简支箱梁的剪切附加挠度计算方法，结果表明，该方法与ANSYS空间有限元模型计算结果及实测结果吻合较好。Zhou等[10]提出了一种用于评价波形钢腹板预应力组合箱梁纯扭性能的改进柔性扭转膜模型，该模型可以有效地考虑混凝土受拉强度、受拉软化行为及混凝土的抗剪行为，经过数值模型及试验数据的对比，它的合理性与准确性得到了相应的验证，如图2所示。Shen等[11]同样建立了用于波纹钢腹板预应力组合箱梁扭转全过程分析的软化膜模型。赵品等[12]提出了一种预测单箱双室波形钢腹板箱梁横向内力及变形的刚架模型，对比实验结果、传统箱梁框架模型和公路桥规中的简支板与连续板模型的横向内力计算结果，发现刚架模型计算结果较规范结果偏小。王兆南等[13]等基于框架分析法建立了波形钢腹板箱梁横向内力解析计算公式，并分析了波形钢腹板厚度、波折角、波长及箱梁宽高比等参数对横向内力的影响规律。

图2 波形钢腹板组合箱梁的扭转模型及验证情况[10]Fig.2 Pure torsional model of the box girder with corrugated steel webs and its verification[10]

1.2 传统箱梁空间分析理论

对波形钢腹板箱梁及普通箱梁理论的研究主要采用解析法(能量法、比拟杆法等)对材料处于弹性范围内的情况而开展，对影响箱梁空间受力行为的许多因素均有不同程度的考虑，但仍存在方法局限性大、不易应用推广等缺点。文献中建立的有限元模型以板壳/实体有限元模型为主，对箱梁空间模型的探讨及应用不足，如单梁、多梁、梁格模型等空间杆系模型的研究缺乏。这些模型虽在计算精度上存在一定的缺失，但从文献[17-20]来看，采用箱梁的高等梁理论(通过引入扭转、畸变、翘曲、剪力滞等自由度形成的多自由度梁模型)来研究箱梁的空间效应，箱梁空间杆系模型的计算精度可以得到有效的提高，在兼有高效计算效率的优势下，形成箱梁结构高效精细的计算方法具有较大潜力。但是，还需考虑复杂的全过程受力行为，使箱梁理论进一步对接桥梁结构体系弹塑性分析理论，拓宽分析理论的适用范围。

2 缆索承重桥梁分析理论

2.1 多塔悬索桥的中塔效应

中国海洋桥梁工程的调研报告指出[21]，多塔长联缆索承重桥梁是一种具有显著技术经济环保优势的桥型。多塔悬索桥在该类型桥梁中占有举足轻重的地位。中国已建成3座多塔悬索桥，包括马鞍山长江大桥(主跨1 080 m)、江苏泰州长江大桥(主跨1 080 m)、武汉鹦鹉洲长江大桥(主跨850 m)。与传统单主跨悬索桥相比，该桥型的两个主跨在受活载偏一侧的作用下，具有较为明显的“中塔效应”(图3)，具体体现为：采用柔性中间桥塔使桥梁的整体刚度降低，而采用刚性中间桥塔则存在主缆与鞍槽的滑移风险。多塔悬索桥中间桥塔的设计涉及桥塔稳定性、主缆滑移及中塔适宜纵向刚度取值等关键问题。

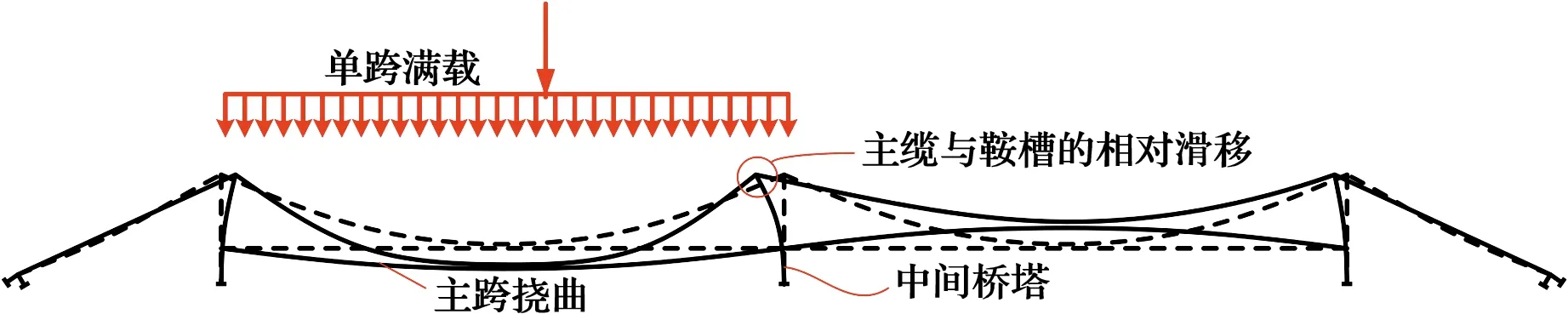
图3 多塔悬索桥的中塔效应Fig.3 Central tower effects of multi-tower suspension bridge

沈锐利、王秀兰及Zhang等学者对多塔悬索桥的中塔效应进行了研究。沈锐利等[22]构建了主跨500～1 500 m范围内的6座三塔悬索桥计算模型，通过改变中塔纵向刚度，对加劲梁竖向挠度及主缆抗滑安全系数进行计算分析，建议了不同竖向刚度要求下中塔纵向刚度的取值范围，如图4所示。从图中可以看出，中塔刚度Kt的对数值与结构刚度基本呈线性关系。王秀兰等[23]以挠跨比和主缆抗滑安全系数为控制指标，提出了多塔悬索桥中塔刚度上、下限值的解析算法，给出了跨径在1 000～2 000 m范围内的中塔刚度取值范围。Zhang等[24]基于分段悬链线理论推导了不等跨多塔悬索桥中间桥塔刚度的解析算法，并对一座跨度组合为248 m+1 060 m+1 360 m+380 m的背景桥梁进行了分析，根据计算分析得到中间桥塔的刚度取值范围为6.615～16.422 MN/m。

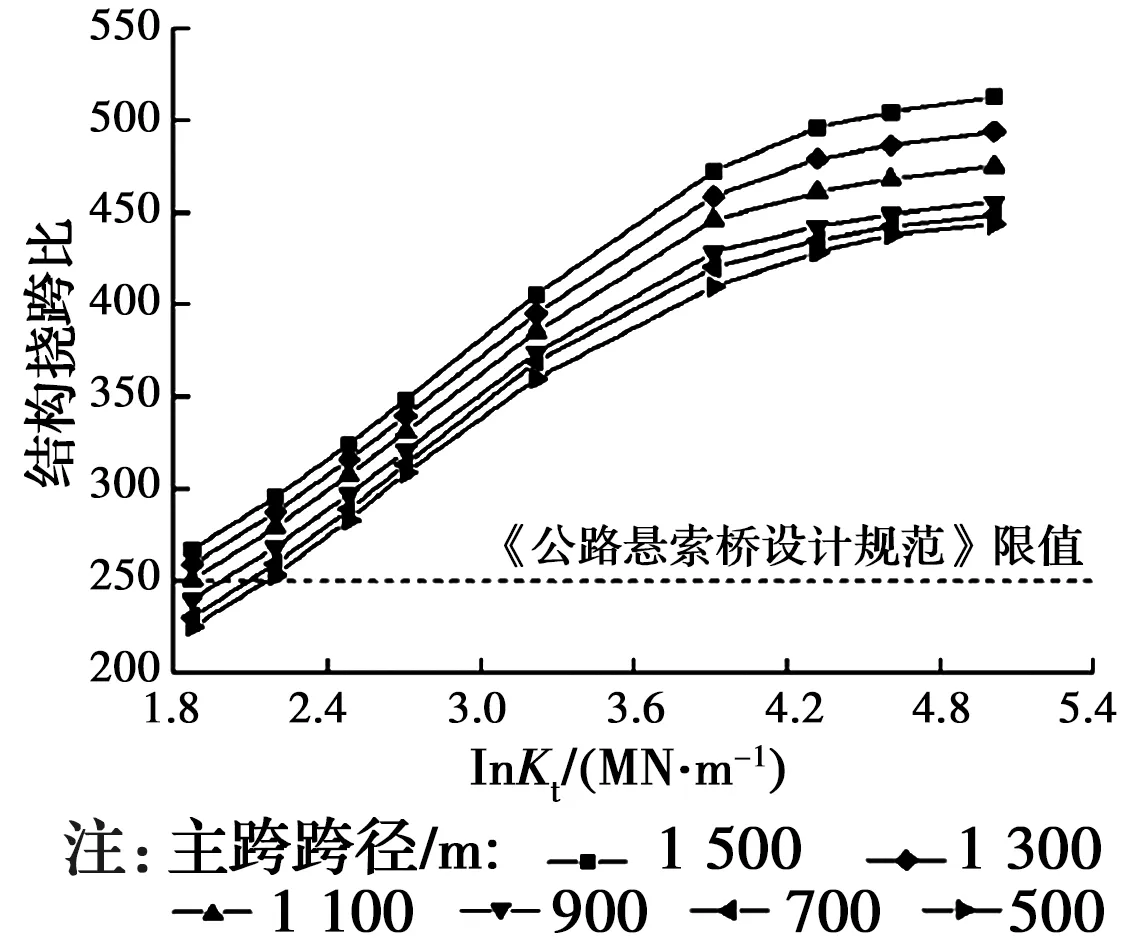
图4 不同中塔刚度对结构刚度的影响[22]Fig.4 Effects of central tower stiffness on structure stiffness[22]

由于桥塔形式多样、分析方法不统一等，现阶段对几座已建多塔悬索桥中塔刚度取值范围并没有完全达成共识，对“中塔效应”的认识存在一桥一议的事实。但自多塔悬索桥建设以来，随相关科学研究工作的不断深入，逐步认识到多塔悬索桥中间桥塔稳定性特征[25]、侧向力对主缆抗滑不可忽略的贡献[26]等，多塔悬索桥中间桥塔(包括主缆抗滑设计在内)的设计正逐步从粗犷、经验、保守的方式转变为精细、科学、合理的方式，相关规范条文也正在积极补充。

2.2 桥梁极限承载力研究

实际桥梁结构的稳定性问题以第二类稳定问题为主，需全面考虑若干非线性因素的影响，特别是几何与材料非线性的影响，属于极限承载力的范畴。桥梁结构应按弹塑性理论分析获得典型的荷载变形曲线及加载过程中桥梁结构的应力、变形等状态，从而充分把握其极限承载模式，明确桥梁设计的安全储备，以保障全桥的静力安全性。关于桥梁极限承载力的研究主要以在建桥梁为背景而展开，笔者主要论述大跨径缆索承重桥梁极限承载力的研究进展。对拱桥的相关研究情况可参考文献[27-30]。

图5 自锚式悬索桥的稳定性定性分析示意图[35]Fig.5 Diagram of qualitative analysis of stability of self-anchored suspension bridge[35]

图6 钢桥板壳有限元模型及残余应力的考虑方式Fig.6 Shell finite element models and various considerations for residual stresses

2.3 钢UHPC桥面板

3 分析理论的工程应用

箱梁与缆索承重桥梁分析理论是与工程实际联系十分紧密的课题，它们关注桥梁建设中最基本的施工与设计，与桥梁工程建设相生相伴。

1)箱梁理论的应用：箱梁空间分析理论中最为突出的问题是顶底板的剪力滞后效应，通过能量法或比拟杆法重新建立波形钢腹板箱梁的剪力滞计算方法，考察了不同形式中剪力滞效应受构造参数影响的情况，如桁式底板波形钢腹板箱梁中底部桁架管件中混凝土的影响、波形钢腹板的褶皱效应等，这些研究结论为该类结构的优化设计提供了指导思路。

2)多塔悬索桥分析理论的应用：目前，有关中塔适宜刚度理论、主缆与中塔塔顶鞍槽滑移理论及抗滑技术及人字形钢桥塔的稳定理论等方面的丰硕成果为中国几座已建及在建的多塔悬索桥提供了理论支撑与技术保障。

3)桥梁极限承载力分析理论的应用：以非线性有限元理论为基础的桥梁极限承载力计算方法具有较多的实现形式，如实体有限元模型、多尺度有限元模型及全杆系有限元模型，以这些模型为载体对斜拉桥、自锚式悬索桥及拱桥进行分析，丰富了各类桥型极限承载力理论的内涵，对一些特殊问题的把握，如多塔斜拉桥中间组合桥塔的承载模式、自锚式悬索桥的面内弹性稳定问题等，不仅有效地消除了设计隐患，也有利于更加客观地认识桥梁结构的非线性物理特征。该理论的发展得益于新的桥梁结构形式的出现，也很好地直接指导了桥梁的建设(图7)。

图7 大跨度桥梁极限承载力理论的工程应用实例Fig.7 Applications of ultimate capacity theories of the large span bridge

4 结论与展望

新型桥梁结构体系，如波形钢腹板箱梁桥、多塔悬索桥、多塔斜拉桥、腹板易屈曲钢箱梁自锚式悬索桥、超高性能混凝土组合桥梁等，催化了桥梁结构分析理论——箱梁与大跨径桥梁理论的发展，波形钢腹板箱梁理论得到了进一步的完善，多塔悬索桥中塔效应问题在更广的参数范围内被讨论，经典桥梁极限承载力理论应用到更多的实际工程中。结合先前关于箱梁与缆索承重桥梁分析理论的讨论，对后续研究提出以下建议：

1)针对箱梁，构件的竖向弯曲、扭转及弯扭耦合效应的研究还需进一步积极开展与完善，需要考虑材料非线性的影响，这些理论属于薄壁构件理论，可以与传统梁理论进行接轨，形成高等梁柱有限元单元，建立高效、精细的箱梁模型，用于构件压弯剪扭复杂力学行为的全过程分析。

2)将箱梁的高等梁理论进一步融入到缆索承重桥梁的非线性分析理论中，同时，应充分重视如混凝土的开裂、钢混组合结构的界面行为及钢板的局部屈曲等力学行为，使桥梁体系杆系模型更加精细。

3)缆索承重桥梁的精细化分析理论还需囊括局部关键区域的分析方法，如悬索桥锚跨区域索股的应力分析、自锚式悬索桥锚固段受力的精细化模拟方法、多塔悬索桥中塔主缆与索鞍相对滑移的精细化计算方法等。

4)随着海洋桥梁工程事业的推进，非等跨三塔悬索桥、超三塔悬索桥等不同类型多塔悬索桥的理论研究需迫切开展。