跨海桥梁上部结构极端波浪(流)作用2019年度研究进展

祝兵，黄博，康啊真，张家玮

(1.西南交通大学 土木工程学院，成都 610031；2.重庆交通大学 土木工程学院，重庆 400074)

随着中国中长期铁路网、公路网从内陆向岛屿的延伸，近年来在沿海区域已经修建了大量的跨海桥梁，如已建成的东海大桥、杭州湾大桥、青岛海湾大桥、港珠澳大桥及平潭海峡公铁两用大桥等，此外，渤海海峡大桥也在规划建设中。诸多跨海大桥的修建，推动中国桥梁建设技术走到世界前列，也为实现中国环渤海湾、长三角、珠三角、台湾海峡，以及国家“21世纪海上丝绸之路”沿线经济区域的互联互通起着举足轻重的作用。

但与此同时，跨海桥梁所处海域的环境极其恶劣和复杂，水深大多在60 m以上，且海浪极高，可能高达10 m，甚至更高，具有海浪周期长及海浪能量极大等特点。在沿海地区，跨海桥梁常会遭受到不同程度的巨浪甚至海啸等复杂的海洋动力环境的侵袭，中国是世界上风暴潮灾害非常严重的少数国家之一，风暴潮灾害一年四季均可发生，从南到北所有沿岸均无幸免，南海诸岛缺乏岛链保护，海啸风险高；台湾岛历史上也曾遭受海啸的严重破坏[1-2]。目前，中国桥梁规范、《海港水文规范》《港口荷载规范》等相关规范中尚无风暴潮等极端波浪(流)荷载的计算方法，不能为跨海桥梁设计、施工提供参考，不能为跨海桥梁的安全营运保驾护航。

长期以来，桥梁工程领域学者们对于桥梁结构的波浪问题研究相对较少。前期研究大部分针对国外较为常见的T型桥梁截面形式，近年来针对中国大范围使用的箱型上部结构形式的桥梁在极端波浪荷载下的受力分析和设计理论研究逐渐增多。针对大型跨海桥梁上部结构的极端波浪(流)作用问题进行回顾，主要对近年来跨海桥梁上部结构承受极端波浪(流)作用下的理论、数值及试验研究与进展进行综述，并对跨海桥梁上部结构与极端波浪(流)相互作用的发展进行展望。

1 理论计算

在理论计算方面，早期涉及到结构极端波浪力计算的研究始于20世纪90年代对于平板以及海洋平台波浪力的研究[3-4]，Wang[5]通过一系列试验研究，验证了他所提出的用于估算各种入射波在平板上引起的最大上升波浪力的计算公式的准确性。Douglass等[6]通过研究飓风中受损的桥梁，提出了估算板式上部结构所受极端波浪力的经验公式。Cuomo等[7]基于1∶25尺度的结构试验，提出了板式桥梁上部结构所受冲击力和准静态力的估算公式。AASHTO(American Association of State Highway and Transportation Officials)[8]基于试验测试结果以及以往研究提出了计算跨海桥梁所受水平力、竖向力以及倾覆力矩的计算公式。Guo等[9]通过水槽试验详细讨论了以往研究所提出的经验公式在估算T型桥梁上部结构所受极端波浪力上的准确性，指出在桥梁上部结构处于淹没状态时，所提出的公式目前能准确估算结构所受极端波浪力。Xu等[10]将以往研究中的极端波浪力通过人工神经网络的训练，提出了T型桥梁上部结构所受的水平力和竖向力的预测公式。Hayatdavoodi等[11]采用Green-Naghdi理论模拟了二维无粘性不可压缩流体，并计算了孤立波作用在淹没状态下板式梁桥上的波浪力。Fang等[12-13]采用势流理论计算了淹没状态下T型上部结构在聚焦波下所受的极端波浪荷载，研究表明，势流理论在计算淹没状态下结构所受极端波浪力具有较高的准确性。势流理论和Green-Naghdi理论具有易于编程和高效求解的特点，在快速估算跨海桥梁所受波浪力的问题上具有一定优势。但是，上述研究中经验公式的提出大多基于数值仿真或水槽试验结果，由于所考虑的波浪参数、结构尺寸以及淹没状态不同，表达形式存在差异。

对于箱型上部结构，Huang等[14]基于1∶30的箱型上部结构波浪水槽试验和前期针对极端波浪力经验公式的研究，指出箱梁结构与T型结构在几何形状上的差异会导致所受波浪力存在较大的差别，以往用于预测T型梁桥面板上的波浪力的公式无法准确计算箱梁桥面板上的波浪力。依据试验现象以及箱型上部结构的几何形状，提出了阻水效应系数的概念来进一步改善Xu等[15]提出的计算方法，同时考虑静水力和水动力，最终提出了计算箱型上部结构桥梁所受极端波浪力的预测公式。该方法基于风暴潮(飓风)特性和箱梁几何特性对箱梁上部结构所受极端波浪荷载的影响，并结合桥梁结构在椭圆余弦波作用下的静水力和水动力特性，通过风暴潮(飓风)特性，椭圆余弦波水质点特性及箱梁上部结构尺寸可以简便估算出箱梁上部结构所受的水平及竖向极端波浪荷载。图1为试验结果与所提出经验公式的计算结果对比图。需要注意的是，目前所提出的经验公式只能用来估算当箱梁底部与水平面时所受的最大极端波浪力，在应用范围以外的极端波浪力估算上无法保证准确性。

针对跨海桥梁箱型上部结构在波流作用下的受力情况，Huang等[16]结合数值波流水槽，研究了波高、周期、水流流速、水深、箱梁淹没系数以及上部结构几何尺寸对极端波流力进行了分析，确定了影响箱梁上部结构所受极端波流力的关键因素。进一步结合回归方法提出了估算箱梁上部结构所受极端波流力的简便公式。该公式选择无量纲的波高(波陡度)形式来确定波力，将其他因素的影响表示为影响系数，最终在一定应用范围内，给出了估算公式。同样，针对孤立波作用下的箱型上部结构受力，Huang等[17]考虑静水和动水波浪力，建立了跨海桥梁在孤立波作用下所受的波浪荷载的理论计算模型，基于水深、波高以及上部结构淹没深度对所受波浪力的影响，通过求解流体静力学和动力学公式既可以求解得到作用在跨海桥梁上的波浪力。同时，为验证所提出方法的优越性，将所提出的计算方法与现有用于估算桥梁上部结构所受的波浪力计算方法进行比较。采用箱梁桥面板的详细尺寸(如图2所示)和特定波浪条件进行计算。详细误差计算结果如表1所示，该估算方法在计算竖向和水平波浪力上具有最小的相关误差，表明所提出的方法在估计箱梁上孤立波诱导的波浪力方面的准确性和有效性。但同样存在适用范围有限的缺点。

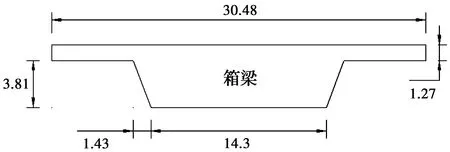
图2 计算所采用的箱梁上部结构详细尺寸(单位：cm)[16]Fig.2 Detailed dimensions of box-girder superstructure used for calculation (unit: cm) [16]

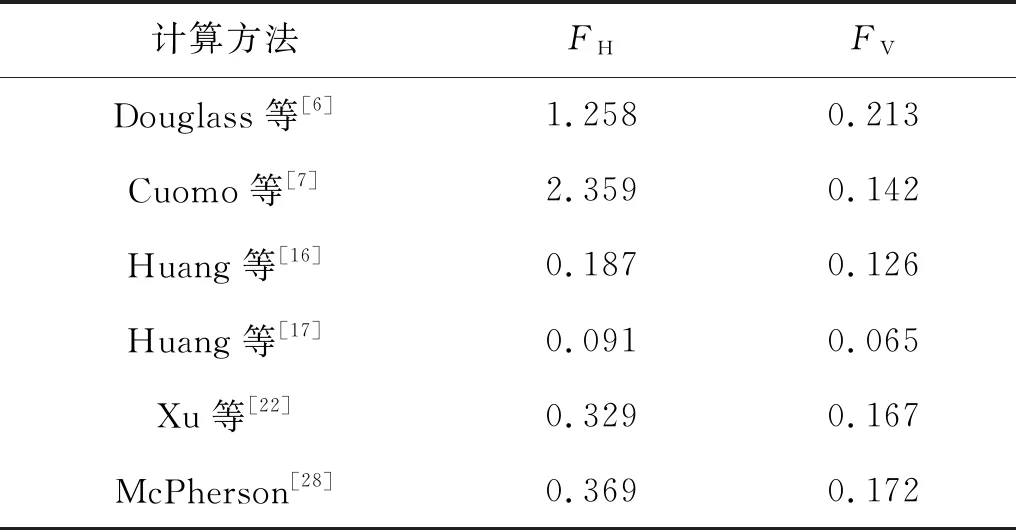
表1 不同计算方法之间波浪力的相关误差比较Table 1 Comparisons of related errors between different empirical methods for wave forces

由表1见，经验公式大多基于水槽试验和数值仿真结果，并且只针对部分波浪参数、特定结构形式或者几种淹没状态，在应用范围以外无法保证估算结果的准确性。同时，势流理论和Green-Naghdi理论也需要假定流体为无粘无旋流体，无法完整模拟波浪与跨海桥梁上部结构相互作用过程中的波浪破碎现象，在估算结构所受冲击力上仍待进一步深入。

2 数值计算

针对箱型上部结构在极端波浪作用下的数值计算，Huang等[14]基于OpenFOAM程序构建了二维数值波浪水槽，采用雷诺时均方程来求解流体运动，用流体体积法来捕捉两相流界面，并结合消波层实现了椭圆余弦波的稳定生成。进一步结合试验测得的箱梁上部结构所受极端波浪力时程，验证了数值水槽的准确性和有效性(如图3)。采用数值仿真的方法能够重现波浪作用在结构上的冲击和破碎情况，有助于结合波浪荷载对箱型上部结构的受力机理进行研究分析。

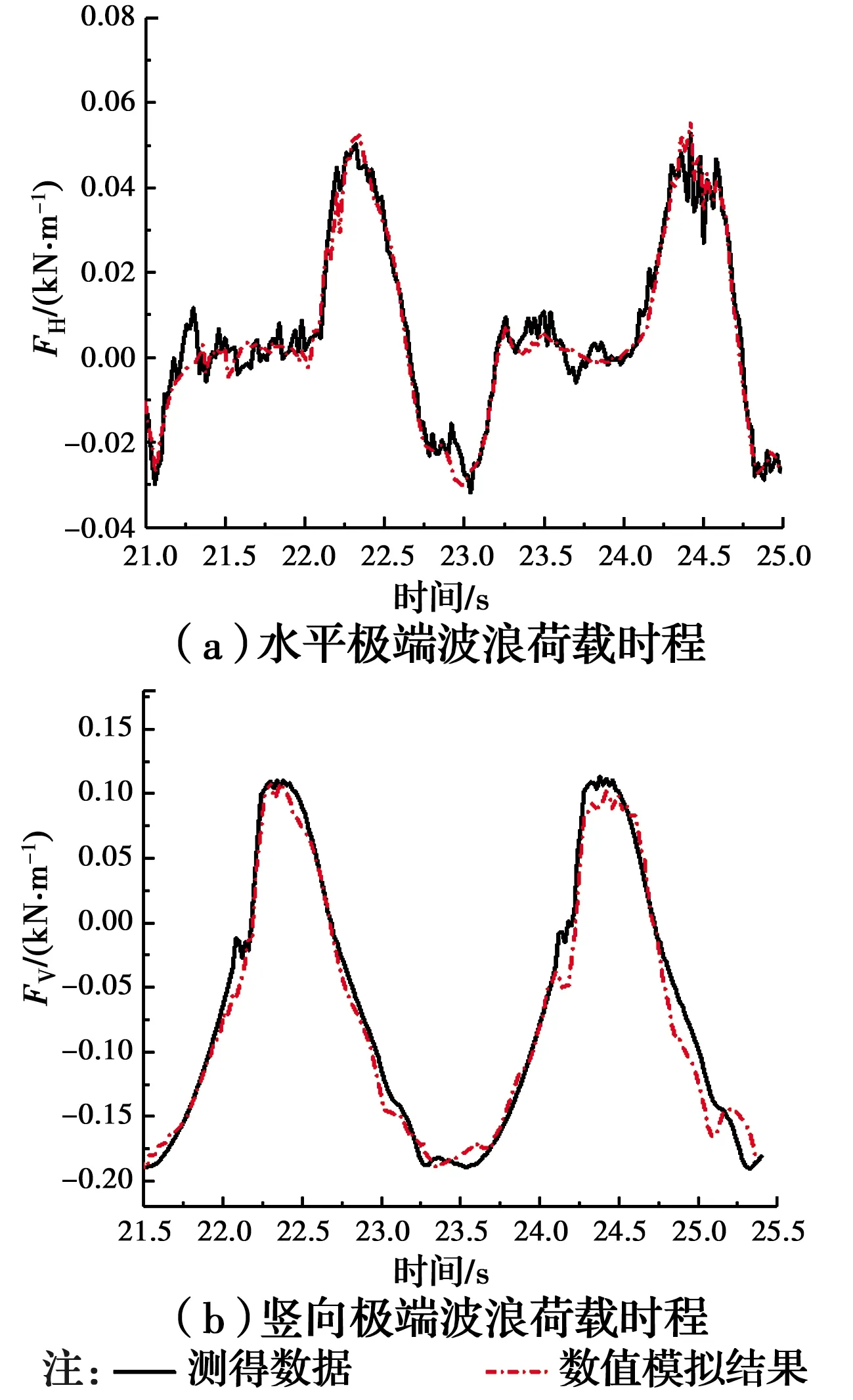
图3 试验结果与数值仿真结果对比图[14]Fig.3 Comparison of experimental results and numerical simulation results[14]

为了研究极端波浪与海流之间的相互作用以及波流共同作用下箱梁上部结构所受波流力，Huang等[16]采用FLOW-3D商业软件并结合源项造波，构建了数值波流水槽，通过在水槽中部添加质量源，并使用随时间变化的体积流率和波面方程实现了Stokes五阶波浪的生成。在入口边界处给出均匀的流速，并根据水槽内部生成Stokes五阶波，实现顺向及逆向波流共同作用的数值模拟。研究表明海流的存在对波流力有显着影响，且与波浪同向的海流将会导致箱型上部结构所受波流力增加。

跨海大桥箱形截面主梁与T形截面主梁由于几何构型差异较大，在极端波浪(海啸和飓风)作用下波浪力有较大差别。杨志莹等[24]采用开源软件OpenFOAM对极端波浪作用下箱型和T型上部结构进行受力分析。分别以孤立波、椭圆余弦波模拟海啸和飓风波浪，假设流体为不可压缩粘性流体，通过RANS(Reynolds-Averaged Navier-Stokes)方程和SST(Shear Stress Transport)k-ω湍流模型描述流体的运动，采用VOF(Volume of Fluid)法追踪自由液面。首先，对数值水槽造波效果及波浪力计算结果进行验证，具体水槽布置图如图4所示，为了避免形成反射波，在入流边界及出流边界处设置消波区，入口采用根据波浪类型、水深等给定的速度边界条件及相分数边界条件，在顶端采用压力进出口边界条件，水槽底面及主梁壁面均为无滑移边界。

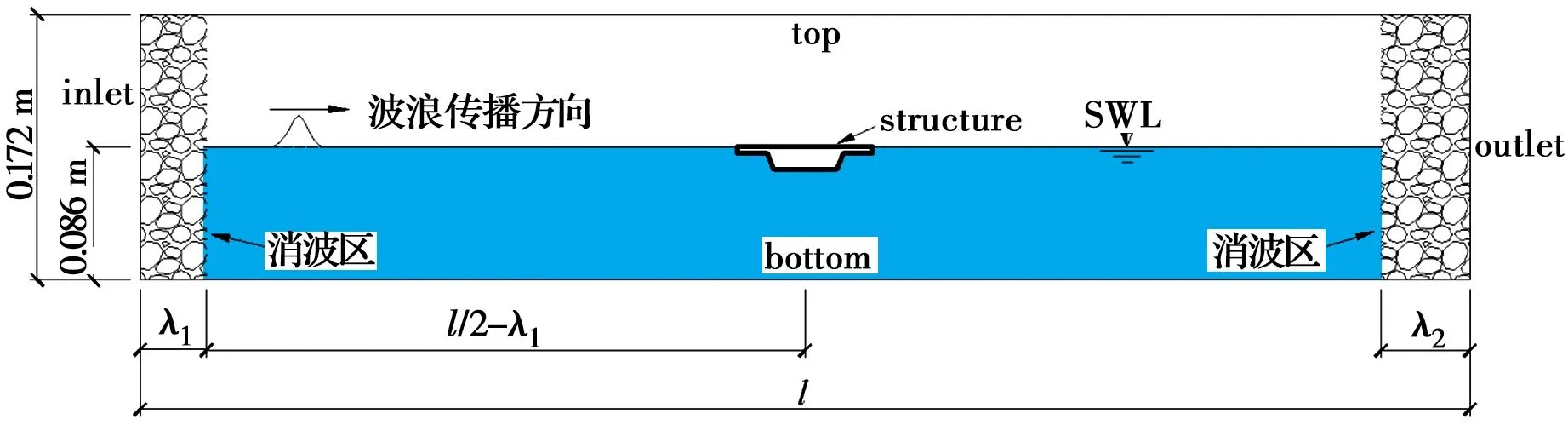
图4 水槽布置图[24]Fig.4 Sketch of wave flume[24]

计算得到的波浪力与Hayatdavoodi的实验结果进行了对比，数值计算验证如图5所示，数值结果与试验结果基本吻合，相对误差较小。在此基础上，分析海啸和飓风作用下，波高及淹没系数对T梁、箱梁受力的影响，并比较二者受力差别。研究建议，对海啸易发海域内的T型上部结构应加强其水平约束，对海啸易发海域内的箱型上部结构应加强其竖向抗冲击约束。

图5 波浪力数值解与试验值对比图[24]Fig.5 Comparison of wave forces between numerical results and experimental data[24]

目前，在极端波浪与桥梁结构相互作用的研究中，大部分研究假定桥梁为刚性结构，在极端波浪作用下不产生变形和位移，但在实际的波浪与桥梁相互作用过程中，桥梁的实时振动状态会引起周围波浪场的改变，从而影响作用在桥梁上的波浪荷载导致振动状态又发生改变，直到达到平衡状态，整个波浪与桥梁相互作用过程具有较为显著的流固耦合特性，刚性结构假定的方法无法完整反映流固耦合场内复杂的相互作用。

3 水槽试验

McPherson[28]为了量化桥梁上部结构所受波浪力，在德州农工大学的Haynes海岸工程实验室中进行了1∶20尺度的模型试验。试验原型参考美国Biloxi海湾90高速公路桥梁，试验分别对平板以及T型桥梁所受波浪力进行了研究分析，并将试验结果与以往专家学者所提出的经验公式相对比，McPherson对比发现现有的计算公式在估算受力上与试验结果存在一定偏差。McPherson结合试验现象和现有经验公式，基于流体静力学提出了较为精确计算平板以及T型桥梁所受波浪力的公式。Shappard等[29]通过波浪水槽试验对I-10埃斯坎比亚海湾大桥所受的波浪力进行了全面研究，研究了水深、淹没深度、波高、周期等参数对桥梁波浪力的影响，并提出了一种具有阻力和惯性系数的理论波浪力模型来估算沿海桥梁所受的波浪力。

Henry[30]研究指出，即使桥梁上下部结构之间存在有效连接，也会在极端波浪荷载作用下产生破坏，Henry通过试验研究了桥梁各部分对桥梁所受总波浪力的贡献，并且针对7种不同的桥梁截面类型和5种不同的桥梁净空对桥梁所受的波浪力进行了分析。研究发现了梁的数量是影响T型桥梁受力的关键因素，并且支撑系统和开孔同样对桥梁受力有一定的影响。Seiffert等[19]和Hayatdavoodi等[20]针对水平板和T型桥梁在夏威夷大学的波浪水槽中进行了二维孤立波试验，试验包括水深、波高和淹没状态对水平板和T型桥梁所受波浪力的影响。试验分析了规则化的波浪力最大值随各类影响因素的变化情况，针对T型桥梁结构，还分析了T梁的梁隔数量以及桥面开孔对波浪力的影响。试验结果表明：淹没状态下的平板所受的向下波浪力随着波高的增加而增大，与波浪传播方向相同的水平波浪力随着波高的增加而增大；抬升状态下的T型桥梁所受竖直上升力随着桥梁抬高高度的增大而减小，竖直向下力和负向水平力同样呈现相同的趋势，但在较深的水域里，竖直上升力随着桥梁抬高高度的增大而增大；T型桥梁的数量对竖直力没有显著的影响，水平力在特定波幅与水深比下随着T型桥梁的数量而略微增大。Guo等[9]对沿海公路桥梁上部结构所受极端波浪力进行了水动力试验，试验在哈尔滨工业大学的大气边界层风洞与波浪联合水槽中进行。试验模型参考广泛用于中国公路桥梁的标准设计图，并且创新性地考虑了包含上部结构、下部结构以及邻近部件的1∶10全桥模型，将除上部结构之外的其他结构组件对波浪场的影响完整地纳入了试验测试中，使试验设计更加符合工程实际。通过波浪力时程和傅里叶谱的分析，他们指出：冲击力在量级上与准静态力相同，并且在桥梁处于零净空状态时达到最大值，建议今后在此类型的桥梁设计中考虑冲击力的存在；水平方向的波浪力与波高成比例，并且随着波浪周期的减小而增大，但是水平方向的冲击力项不明显；提出了用于计算此类桥梁所受极端波浪力的估算公式，并通过与以往文献的经验公式对比验证了所提公式在计算桥梁极端波浪力上的准确性和有效性。Hayashi[31]进行了小规模实验来研究海啸波浪力对箱梁桥面板的影响。详细讨论了箱梁桥面板上的海啸波浪力，将实验中测得的最大水平波浪力和垂直波浪力转换为实际桥梁所受波浪力的值，将其与目标桥梁的静载荷进行了比较，并对箱梁和T梁的波浪力进行了简要比较。张翔宁[32]选取建设中的主梁结构为箱梁式的福建平潭海峡公铁两用大桥为研究对象，在无反射波浪水槽中建立主梁结构的断面物理模型，研究了箱型上部结构在波浪力作用下的破坏机理，并讨论了箱型上部结构淹没状态对其所受波浪力的影响规律。

张家玮等[33]在波浪水槽中进了1∶30的箱梁所受极端波浪力的水动力研究，进行了一系列70个试验，包括6种波浪高度，3种类型的桥面板高程和多种水深。含有的5种类型的淹没系数覆盖了全部桥面板高程和淹没条件，波浪水槽长68 m、宽1 m、高1.6 m。由无反射造波机在水槽的左侧产生周期波浪。根据波浪槽中波浪运动的实时信号产生入射波和消除波的组合波，可以通过自动调整的波浪吸收方法消除入射波的反射对造波产生的影响。波浪吸收器由海滩鹅卵石制成，坡度为1∶5，位于波浪水槽的右侧，用于减少波浪反射对水槽中波浪传播造成的影响并吸收波浪能量。他们对极端波浪力时程进行了详细讨论，并结合傅里叶分析，将波浪力中准静态力和和和冲击力进行了分离，同时与试验快照对比分析(图6)，详细研究了箱梁上部结构在极端波浪作用下的受力机理。研究发现：梁体处于淹没状态时，浮托力作用大大减轻梁体的有效自重甚至超过梁体自重，在水平力和倾覆弯矩的联合作用下导致了梁体的脱落破坏，不同类型的截面形式(如T型梁、板梁、钢桁架等) 受波浪力作用的结果可能存在差异，应进一步研究比较并区别考虑。

图6 试验快照[33]Fig.6 Snapshot of wave flume test[33]

Zhang等[34]针对波流作用下箱梁上部结构的破坏形式和机理，在中型波流水槽中开展了1∶30比尺的水槽试验，测试了不同波高、流速、周期和淹没深度等条件对于箱梁上部结构波浪力影响，并进一步结合数值仿真(如图7)讨论了箱梁在风暴潮引起的极端波流作用下的破坏形式。研究发现，在淹没深度较小的情况下，正向水流通常会导致正向水平力的增大和竖向力的减小。逆向水流作用正好相反。然而，由于波浪力受到波面与结构物相对位置关系的影响，当淹没深度增加时，逆向水流对于波浪力的影响存在一定差异，甚至产生相反的规律。Fang等[35]开展了1∶10缩尺比的桥梁模型波浪水槽试验，试验中采用一个完整的主梁桥跨、两个1/4长度的临跨和两座桥墩，完整考虑了临跨和桥墩边界对波浪场的影响，试验研究了不同波浪要素的正向入射波浪和斜向入射波浪作用下上部结构在不同淹没状态下的受力情况，并讨论了不同波浪入射角度对波浪力的影响规律。

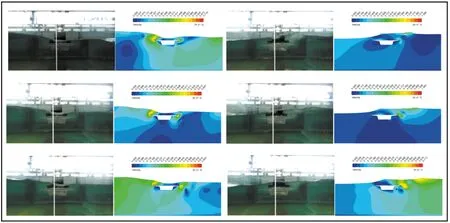
图7 箱梁上部结构在波流作用下的试验与仿真结果对比[34]Fig.7 Comparison of experimental and simulation results of box girder superstructure under the action of wave and current[34]

4 展望

中国将在海况恶劣的环境中建设更多更具挑战性的跨海大桥，然而海洋环境与陆地环境差异明显。跨海桥梁不仅面临着水深，急流的威胁，以中国主要跨海通道为例，桥梁还会频繁受到台风影响，因此，海洋环境灾害模拟、海洋环境荷载计算以及桥梁结构响应一直是桥梁工程中较为关心的问题。通过学者们的不懈努力，已经对跨海桥梁的相关极端波浪(流)作用问题展开了探索，但该领域需要研究和解决的问题还有很多，以下几个方面的研究对于深化跨海桥梁箱型上部结构海洋灾害致灾机理的认识、推动跨海桥梁防灾减灾研究具有重要的作用：

1)现有极端波浪(流)作用下跨海桥梁的数值模拟大多采用二维模型，导致无法考虑绕流以及滞留空气对极端波浪荷载的影响。需进一步发展数值仿真技术，构建三维数值波浪水槽，开发准确的两相流捕捉技术，精确研究跨海桥梁与极端波浪(流)相互作用下的流场和波浪力情况。

2)目前，桥梁规范、港口荷载规范等尚无完善的波流荷载作用条文，难以适用于复杂海洋环境地区。需进一步发挥水槽模型试验的优势，开展与跨海桥梁桥址区实际海洋条件更加相符的波流参数水动力试验，研究风、浪、流等组合条件对于桥梁基础和上部结构的作用。

3)需基于更高效准确的数值方法建立精细化极端海洋环境作用的数值计算模型，如流固耦合方法、SPH方法等。通过试验和数值模拟进一步研究波浪冲击、结构选型等对于桥梁上部结构波流力的影响，提出用于工程的极端波浪(流)力计算方法和减弱波流作用的有效防护措施。为跨海桥梁工程施工和全桥运营的可行性、安全性和经济性提供支持。

4)目前的研究中较少考虑桥梁结构的动态响应，而包含动态响应的研究中采用的耦合算法是在一个或多个时间步后进行流体与结构之间的数据交换，流体与结构的计算推进是各自独立的，在计算耦合效应对波浪力以及结构动态响应的影响时具有一定的局限性，难以揭示跨海桥梁在极端波浪作用下的破坏机理。因此，亟需研究考虑流固耦合效应时跨海桥梁在极端波浪作用下的失效模式和破坏机理，发展对应的防灾减灾措施。