桥梁风工程2019年度研究进展

廖海黎，李明水，马存明，王骑，孙延国，周强

(西南交通大学 a.土木工程学院；b.风工程四川省重点实验室，成都 610044)

近年来，中国大跨度桥梁的建设成就举世瞩目。在中国迈向世界桥梁强国的进程中，桥梁风工程研究为大跨度桥梁设计提供了关键技术支撑。中国桥梁风工程科研工作者与桥梁设计工程师合作，解决了数百座大跨度桥梁的抗风设计问题。伴随大跨度桥梁的发展，中国在桥梁抗风基础理论研究及工程实践能力方面取得了长足进步，已居于世界前列。

作为一门具有交叉学科性质的技术门类，桥梁风工程涉及气象学、结构动力学、空气动力学、流固耦合力学、风洞试验技术等多门学科，为桥梁抗风设计提供了理论基础、方法及手段。桥梁风工程研究的主要问题是桥梁结构和构件的风致振动及其控制。笔者围绕大跨度桥梁抗风设计中的主要问题——桥位风特性现场实测、桥梁非线性颤振特性及计算理论、桥梁抖振计算理论和桥梁涡激振动计算理论及控制，介绍了2019年以来主要的研究进展。

1 桥位风特性现场实测研究

风特性是桥梁抗风设计的基础资料，对桥梁设计方案的成立及桥梁造价，对桥梁抗风安全性、行车安全性和舒适性等影响巨大。风特性研究的首要手段是现场实测，其次是风洞试验物理模拟和CFD(computational fluid dynamics)数值模拟。迄今为止，抗风设计中有关风特性的“成熟知识”多是依据良态气候的大陆季风实测得来。对于控制沿海桥梁及海洋桥梁抗风设计的台风，由于很难开展系统性实测，至今对其特性的掌握还远不够。山区桥位的风特性受复杂多变的气象、地理因素影响，远比平原风特性复杂，迄今对其认识也很有限，这给山区桥梁抗风设计造成了很大困扰。龙卷风、下击暴流等特异风方面，也很缺乏针对桥梁设计需要的风特性研究。

1.1 台风风特性实测

在台风风场实测方面，Zhao等[1-2]分别基于多普勒激光雷达的实测数据和西堠门大桥健康监测系统获得的系列台风记录数据，对台风外围风场的平均风剖面演变特性和脉动风场特性进行了分析，如图1所示。对于平均风剖面，研究发现，台风外围除了存在常见指数律的风剖面，在远场还存在S形和反C形两种风剖面形态；对于脉动风场特性，研究发现，台风外围风场的脉动风特性中的偏度可忽略不计，非高斯特性也不显著，即与良态气候强风类似，符合高斯分布，且3个方向上脉动风速功率谱与Von Kármán谱较为吻合。Kim等[3]也通过现场实测研究了台风的风谱特性。Tao等[4]对苏通长江大桥健康监测系统获得的台风数据进行了频谱分析，建立了考虑高频子区的改进功率谱密度模型。张传雄等[5]对台风“玛莉亚”风场进行现场实测，发现其风速剖面与指数律模型接近，但边界层高度平均值为1 421 m，比规范建议值及实测良态风均值要大。方根深等[6]结合台风在中国沿海登陆过程中风场参数实测数据，提出了适用于中国东南沿海区域的考虑多个场参数之间相关性的台风风场改进数值模型，给出了4类典型地貌下台风气候风剖面拟合关系。需要指出的是，目前，现场实测得到的大多为台风外围风场数据，且大多认为其风场特性与良态风特性较为吻合，但由于台风中心风速难以捕捉、测量，有关台风中心附近的风场特性还有待进一步深入研究。

图1 文献[1-2]现场实测得到的台风特征Fig.1 Profiles and spectra of typhoon

1.2 山区峡谷风特性实测

在山区大跨桥梁桥位的风场实测方面，2019年学者们开展了较多研究，取得了一批新成果。Liao等[7-8]采用多普勒激光测风雷达测量了某山区峡谷地形下竖直平面内不同高度处的风速时程序列，获取了山区平均风速、紊流强度、紊流积分尺度、风速空间相关性和紊流风速谱随高度的变化特征(图2(a)、(b))，发现大风情况下平均风速的风向与山谷走向基本一致，紊流强度无论是沿竖向的分布特征还是3个方向分量的比值，均与平原和沿海地区存在较大差别，且相较于Simiu谱和Panofsky谱，Von Kármán谱更适合描述山区的脉动风场。Yu等[9]在泸定大渡河大桥的猫道上沿纵向布置了5套风速传感器，分别采用平稳和非平稳风速模型对比分析了脉动风场特性，表明局部地形对山区平均风和紊流风特性的影响都很大，山区风非平稳性质极为突出(图2(c))，还发现山区风3个方向上的脉动风速功率谱密度函数更符合Von Kármán谱。张志田等[10]同样在深切峡谷桥位处风场实测中发现，Von Kármán谱用于描述山区脉动风场特性的吻合程度更好，且深切峡谷对风向有比较强的锁定作用。郭增伟等[11]分析了三峡库区峡谷风场的非平稳性，发现相比沿海地区，山区风在幅值和频率方面均表现出更强的非平稳特性。综合近年来的实测研究成果，学者们在山区风场特性研究上取得了一些共识：1)地形是影响山区桥位风场的最主要因素，峡谷走向对来流风向的锁定作用明显；2)山区风场紊流强度与规范值存在较大差别，因此，更宜根据现场实测值确定抗风设计参数；3)Von Kármán谱更合适表述山区风场3个方向上的脉动特性；4)相较于沿海和平原地区，山区风场的非平稳特性更显著。

图2 山区现场实测脉动风速特征[7]Fig.2 The characteristics of turbulence over mountainous area[7]

2 大跨度桥梁非线性颤振研究

颤振作为大跨度缆索承重桥梁抗风设计的首要因素，一直是桥梁风工程研究的热点。历经几十年的发展，传统的桥梁颤振线性分析理论已日臻成熟。对于大跨度桥梁的“硬颤振”，当考虑平均风荷载引起附加攻角等非线性效应后，线性理论能够给出与全桥气弹模型风洞试验精度相当的预测。随着超大跨度桥梁的发展，由于全桥气弹模型的缩尺比越来越小，抗风设计将更加倚重于高精度的三维颤振分析[12-13]。对于大跨度桥梁的“软颤振”，由于不存在明显的颤振临界状态和具有显著的气动力非线性，正如陈政清[14]指出，基于特征值分析的线性颤振分析理论无法描述这种软颤振特性。因此，近年来桥梁非线性颤振及其计算理论成为研究的新热点。

总的来说，大跨度桥梁的非线性颤振研究主要围绕颤振后现象(软颤振)特性和极限环(软颤振振幅)求解两个方面。对于现象研究，很多学者都通过风洞试验测试并记录下了桥梁断面发生软颤振时的稳定振动现象(极限环)，研究结论具备共同特征：颤振后的稳定振动也是弯扭耦合形式，并受到桥梁气动外形、风攻角和结构阻尼的显著影响，目前，大跨度桥梁广泛采用的4种典型主梁(П型梁、流线型箱梁、分体箱梁和桁架梁)均可能发生软颤振。2019年以来的主要研究成果如下：唐煜等[15]研究了П型梁的颤振后特性，指出该类型断面的软颤振受风攻角和结构阻尼的影响显著，弯扭耦合振动特征明显；高广中等[16]的研究表明，扁平箱梁软颤振的弯扭耦合特征明显，且当振幅较大时，自激力中含有明显的高次谐波分量；伍波等[17]研究了扁平箱梁的耦合软颤振特性，获得了随振幅变化的非线性颤振导数，解释了典型软颤振现象的动力学机理；朱青等[18]研究了闭口箱梁在大风攻角下的软颤振特性，并基于半经验非线性气动力模型提出了软颤振起振风速的判定方法；Zhou等[19]基于非线性气动力模型计算了分体式箱梁的颤振性能，发现增设中央稳定板后硬颤振转变为了软颤振；伍波等[20]研究了双层桁架梁弯扭耦合软颤振特性，解释了其发生、发展的动力学机理。

对于计算方法，目前分为两类：1)计入自激气动力高次谐波分量随振幅变化的非线性计算方法；2)仅计入线性谐波分量随振幅变化的线性计算方法。对于第一类非线性颤振计算，主要源于研究者在自激气动力中发现的高次谐波分量，并将其计入到计算中。代表学者是高广中等[21-23]、许福友等[24]，其共同点是：通过风洞试验或数值模拟观察到了桥梁断面显著的气动力高次谐波分量，根据气动力的高次谐波分量占比以及气动力是否做功进行取舍，在泰勒展开模型的基础上，构建了只包含1次和3次谐波参数项的气动扭矩模型，然后运用非线性动力学方法或能量平衡法对单自由度扭转颤振极限环(扭转软颤振稳定振幅)进行求解，代表性的研究结果如图3[21]和图4[24]所示。

图3 风洞试验获得的扁平箱梁断面软颤振时力矩的高次谐波分量[21]Fig.3 Amplitude spectra Wind-induced forces on a box girder by wind tunnel test[21]

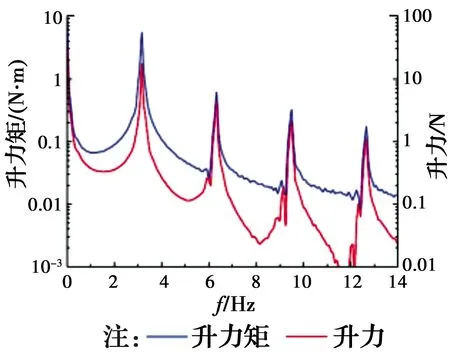
图4 数值计算获得的扁平箱梁断面软颤振时升力和力矩的高次谐波分量[24]Fig.4 Amplitude spectra Wind-induced forces on a box girder by numerical simulation[24]

对于第二类非线性颤振计算，源于研究者在中等振幅条件下(扭转振幅小于10°)并没有在气动力中发现明显的高次谐波分量[25]，而仅发现了线性分量(颤振导数)随振幅的非线性变化，继而沿用线性颤振的闭合解理论，提出了耦合软颤振的计算方法，代表性的工作见文献[26-27]。目前，该方法已通过风洞试验进行了验证(如图5所示)，并从二维拓展到了三维，从而为大跨度桥梁多模态耦合软颤振的计算提供了一种有效手段。

廖海黎等[28]对近20年来大跨度桥梁颤振研究进展进行了综述，重点介绍了非线性自激气动力和非线性颤振的研究成果，提出了发展多模态耦合软颤振分析理论的必要性，并指出需要科学制定“软颤振”的设计评价准则。葛耀君等[29]率先将结构强健性的理念引入到桥梁抗风设计方法与颤振评价中，指出强健性包含强度、刚度和稳定性3个方面，并建议采用等效中心点法来计算颤振强健性的可靠性指标、失效概率和重现时间。强健性评价方法目前虽然采用了硬颤振的临界风速作为参考，但无疑具有更大拓展空间，通过引入表征结构强度安全参数和软颤振失稳风险指标，可望发展形成桥梁软颤振安全评价方法和准则。

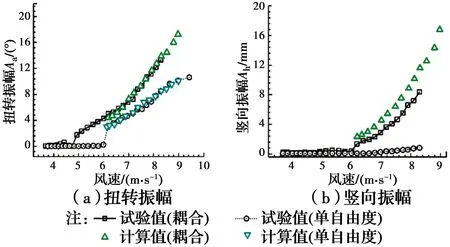
图5 软颤振振幅的计算值与风洞试验对比[27]Fig.5 Comparison of soft flutter amplitudes using wind tunnel test and numerical simulation[27]

3 桥梁抖振计算理论研究

由于脉动风作用引起的抖振是构成桥梁结构动力风荷载和随机响应的主要因素，是抗风设计中进行结构安全性和行车舒适性评价的重要依据。为了提高抖振计算精度，一些学者一直着力于构建和完善更为精确的抖振力模型和计算方法。近年来，关于大跨度桥梁抖振方面的进展主要集中在以下3个方面：一是桥梁主梁抖振气动力研究；二是大跨度桥梁抖振响应分析方法；三是非平稳风作用下的桥梁抖振响应研究。

在抖振气动力方面，张志田等[30]基于Küssner函数对抖振力和气动导纳在时域内进行模拟，并比较了不同气动导纳函数对桥梁抖振响应的影响，研究发现，基于Sears函数计算的抖振响应明显高于试验值。Li等[31-32]基于三维抖振理论，探明了控制紊流三维效应强弱的关键参数，并给出了抖振力展向相干函数的一般形式。通过引入气动导纳修正项经验模型，在紊流场中直接识别了典型桥梁断面的二维气动导纳(图6)，为抖振力精细化分析提供了重要依据[33]。Ma等[34-35]根据风洞测压试验结果，建立了流线型箱梁的三维气动导纳经验模型，该模型充分考虑了湍流的三维效应，并与现场实测的气动导纳进行了对比分析。以上研究均针对静止的桥梁断面，而实际桥梁处于振动状态，为此，Yan等[36]提出了一种将气动力分离为自激力和抖振力，然后根据提取的抖振力来计算气动导纳的试验方法，并通过该方法对处于自由振动状态下的流线型箱梁的气动导纳进行了识别。结果显示，气动导纳与桥梁主梁振动状态有关，因此，有必要考虑实际桥梁振动对气动导纳的影响。另外，Cheynet等[37]在现场实测桥梁流场畸变的基础上，研究了抖振力、气动导纳模型以及片条假设的有效性。在数值方法上，Kavrakov等[38]提出了一种基于二维涡粒子法的计算流体力学(CFD)方法来识别六分量复气动导纳(图7)，并与试验结果进行比较，验证了该方法的可行性。与上述试验方法相比，该方法可以很好地控制不同方向脉动分量对气动导纳的影响，并从微观层面上解释了相关气动机理。此外，通过该方法还可以进一步检验气动力的可叠加性以及研究紊流度对气动导纳的影响。

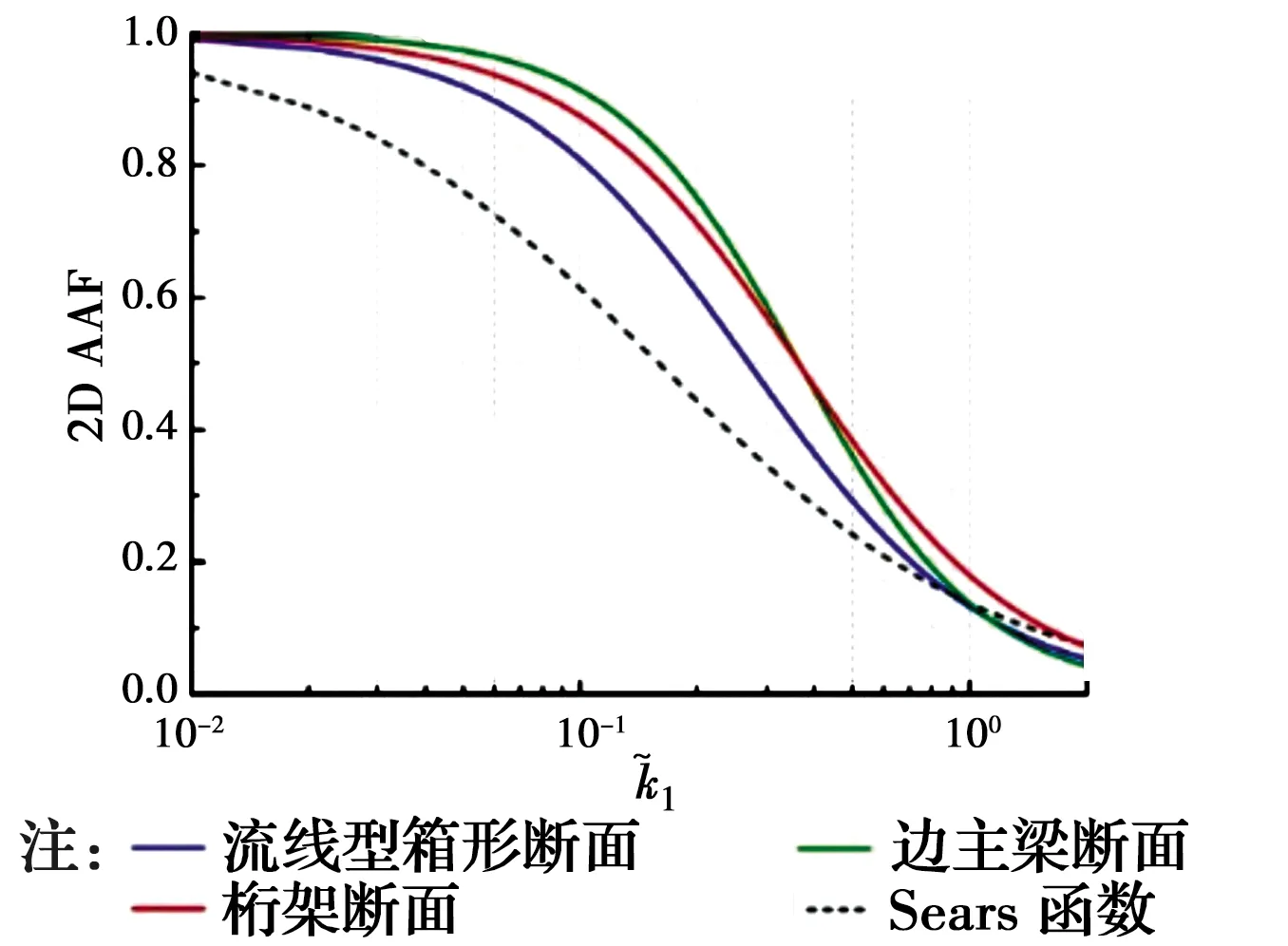
图6 典型桥梁断面的二维气动导纳[33]Fig.6 Two-dimensional aerodynamic admittance of a typical bridge section[33]

图7 桥梁断面周围瞬时速度场[38]Fig.7 The instantaneous velocity field around the bridge section[38]

在抖振响应分析方法方面，Xu等[39]指出抖振应力分析是评估强风区大跨度桥梁局部破坏和疲劳损伤的重要手段，并基于风振压力正交分解和子结构有限元模型，建立了用于大跨度箱梁桥抖振应力分析的研究框架，并通过与现场相比较验证了该方法的可靠性(图8)。苏益等[40]提出了不依赖于湍流场特性的综合传递函数，该函数包含了气动导纳和机械导纳的影响，可以成功预测不同风场环境下大跨度桥梁的抖振响应。基于Ribner三维气动力理论，Li等[41]建立了考虑紊流三维效应的大跨度桥梁抖振频域分析方法，通过研究紊流三维效应对抖振响应的影响(图9)，明确了传统抖振分析理论的适用条件，从而使抖振分析理论更加完善。董锐等[42]提出了大跨度桥梁多目标等效静力风荷载基向量法，研究表明，该方法获得的多目标等效静力风荷载在抖振响应计算精度和荷载分布的合理性方面均表现良好。

图8 跨中主梁断面抖振应力[39]Fig.8 Buffeting stress of the deck at mid-span[39]

近年来，非平稳风作用下桥梁的抖振响应问题受到研究者的重视。陶天友等[43]以苏通大桥为工程背景，针对台风非平稳性显著的特征，开展了大跨度桥梁非平稳抖振时域模拟与分析。苏延文等[44]针对山区桥梁，考察了强弱非平稳风速对大跨桥梁抖振响应的影响，如10所示，结果表明，对于非平稳指标较强的实测风速样本，需要进行精细化的非平稳瞬态响应分析。

图10 强非平稳风作用下主梁的侧向抖振响应[44]Fig.10 Lateral buffeting response of main girder within strong non-stationary wind[44]

4 涡激振动计算理论与控制技术研究

涡激振动作为在桥梁主梁、吊杆、拉索等构件上频繁发生的限幅振动，可能会对桥梁行车舒适性和构件疲劳寿命造成危害。改善涡振振幅的预测精度是涡振计算理论研究的主要目的，开发经济有效的涡振控制技术是桥梁抗风设计的实际需求。

为探明主梁涡振致振机理及其影响因素，胡传新等[52]采用不同尺度的流线闭口箱梁模型，研究了涡激气动力的雷诺数效应，结果表明，不同雷诺数下涡振响应和涡激力分布均明显不同：雷诺数大，涡振响应也大，但涡振起振风速反而降低。Sun等[53]研究了矩形、梯形和流线型箱梁断面的涡激力特性及其跨向相关性，指出不同断面形状的涡振致振机理不同，涡激力的跨向相关性强弱由自激力(SEF)和涡脱力(VIF)的占比确定。Ma等[54]在方形断面桥塔气弹模型试验中发现不同模态之间涡振与驰振的耦合振动现象，且该种振动形式与二维范畴内的耦合振动有明显区别。Li等[55]通过现场实测发现，实际桥梁的涡激振动具有时变特性，并提出了一种识别时变气动力的算法，用以从实测数据中捕捉涡振现象。Xu等[56]基于现场实测大数据分析，提出了大跨度桥梁涡激振动识别方法，建立了涡激振动预测模型。另外，一些学者还开展了主梁构造细节[57-58]和双幅箱梁[59]间距对涡激振动性能的影响研究。

Li等[60]通过风洞试验研究了表面光滑的平行钢丝股索(PWS)和粗糙的钢丝绳股索(WR)悬索桥吊杆的气动干扰和尾流涡振问题，研究表明，平行钢丝股索的空间不稳定区域较钢丝绳股索多，下风向钢丝绳股索的振幅一直随着风速的增加而增加，而平行钢丝股索的振幅会趋于平稳或减小。赵燕等[61]利用大涡模拟法研究了悬索桥双吊索的气动干扰和尾流涡激振动问题。祝志文等[62]基于现场实测，针对斜拉索模态密集的特点，利用解析模态分解法研究了斜拉索涡激振动的时频域特性。

涡振控制的目的是对桥梁主梁或吊杆、斜拉索等细长构件的涡振进行抑制，工程上常见的控制措施有气动措施和机械措施两类。赵林等[63]针对大跨度桥梁中常见的4种主梁形式(双边主梁、整体式箱梁、分体式箱梁以及桁架梁)，梳理和归纳了常用的各类涡振气动控制措施。Hu等[64]和张天翼等[65]分别研究了各种附加气动措施(扰流板、导流板、风嘴、稳定板、导流板、裙板)对箱梁和双箱型边主梁涡激振动的抑振原理和效果。华旭刚等[66]指出大跨度悬索桥存在多阶模态涡激振动问题，提出可采用电涡流阻尼器对漂浮体系悬索桥进行半主动控制。Chen等[67]提出了一种新的涡振控制思路，即在主梁断面布设被动吸/吹气孔道，扰乱涡振发生时的流场分布和旋涡形成，从而实现对主梁涡振的抑制(图11)。基于同样的思路，在斜拉索上安装被动自吸/吹气控制套环来抑制其涡激振动[68]。Zhang等[69]基于数值模拟提出利用被动式漩涡发生装置来抑制涡振，研究发现，在梁底间隔安装旋涡发生装置后，原断面规律性的旋涡脱落被扰乱，旋涡的强度和展向相关性都被削弱，从而使涡振振幅得以降低(图12)。

图11 被动吸/吹装置示意图Fig.11 Layout chart of slits and conditions

图12 主梁旋涡发生装置示意图Fig.12 Arrangement of vortex generators

传统的TMD尺寸较大，难以布置在流线型箱梁内部实现对涡激振动的控制。针对这一局限，Xu等[70]提出使用尺寸较小的惯容器来抑制涡激振动，理论分析表明，惯容器的引入使TMD最优频率远高于结构特征频率，从而显著降低了TMD弹簧静变形，使其能够安装到流线型扁平箱梁内部，实现对大跨桥梁涡振的有效控制(图13)。另外，Liu等[71]还研究了粘弹性阻尼器对斜拉索涡激振动的抑振效果。

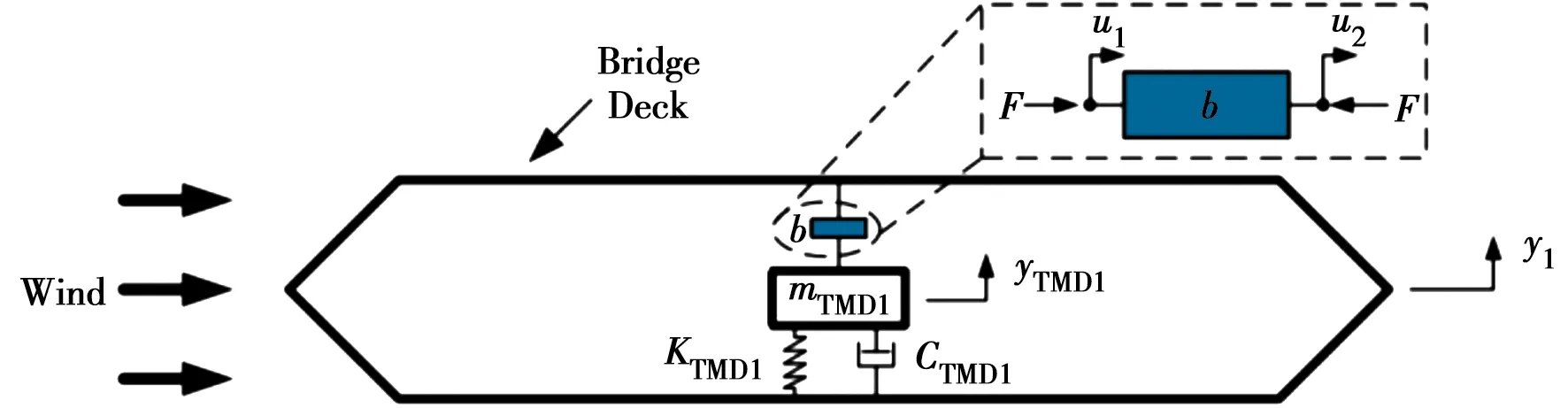
图13 TMDI系统涡振控制示意图Fig.13 Single-degree-of-freedom primary structure incorporating with a TMDI system

正如葛耀君等[72]指出的那样：未来的涡振研究在围绕新型观测设备和试验技术、高精度气动力降阶模拟和人工智能手段、主动气动控制措施和新型被动机械措施等方面有较大的深入研究的空间。

5 结论

桥梁风工程对山区风、台风和特异风等风场特性的认识还远未成熟，需要研究者们通过长期、大量的现场实测，在掌握第一手资料的基础上获得对风特性的深入认识，为改进桥梁抗风设计理论提供更为可靠的依据。超大跨度桥梁和海洋桥梁的发展要求抗风设计理论不断创新，非线性和紊流对桥梁风致响应的影响越来越不容忽视，传统的偏于保守的某些设计准则也需要改进；还需要发展更为经济有效的风振控制技术、开发更为优良的桥梁气动外形及结构形式，以适应超大跨度桥梁的发展。人工智能、大数据等新科技手段，有望成为解决桥梁风工程复杂问题的有效途径。