基于二元分割检测分段线性趋势中的多变点*
刘 伟, 胡 尧, 2**, 胡 倩
(1.贵州大学 数学与统计学院, 贵阳 550025; 2.贵州省公共大数据重点实验室, 贵阳 550025)
0 引 言
变点检测问题一直是统计学中一个经典的分支, 最初起源于Page在Biometrika上发表的一篇关于连续抽样检验的文章[1], 这是一篇关于质量检测问题的理论研究, 从此开启了变点研究的篇章。在如今的大数据发展趋势中, 掌握数据中的突变对于分析数据, 挖掘其中的隐藏信息有着至关重要的作用, 所以越来越多的统计学者投入到这一研究领域[2-3]。近年来, 变点检测问题已被广泛应用于各个领域, 在许多行业中, 都能看到变点的身影,例如自动检测云数据中的变点[4], 以保持应用程序或网站的性能和可用性; 热带气旋数据中的气候变化检测[5], 能及时预防重大自然灾害;根据光曲线数据的变化能检测系外行星; DNA拷贝数的突变跟某些疾病的起因密切相关[6]; 对潜在协整股票价格的平稳区间的估计可以降低损失的风险[7]等。
所谓的变点, 就是在一个时间序列或过程中, 当某个统计特性在某一时刻τ突然发生了变化, 就称该时刻τ为变点, 统计特性包括样本的分布类型、分布参数、数字特征等, 变点检测就是利用统计量或统计方法将该时刻τ估计出来。在数据被假定为分段恒定的情况下, 一类常用的方法是基于最小化成本函数的思想, 如Jackson等[8]提出的OP(Optimal Partitioning)算法, 该算法是在成本函数中引入惩罚项, 将变点检测转化为成本函数惩罚最小化问题, 但是在数据量比较大的情况下, 计算比较复杂;所以Killick等[9]提出基于不等式修剪的PELT(Pruned Exact Linear Time)算法, 它比OP更有效且计算简单;而Maidstone等[10]将PELT与pDPA(pruned Dynamic Programming Algorithm)相结合,提出一种更稳健高效的FPOP(Functional Pruning Optimal Partitioning)算法等。而在数据具有线性趋势变化的相关研究中, Bai和Perron[11]考虑通过最小二乘法估计具有多个结构变化的线性模型, 并针对无变化的原假设提出Wald型检验; Kim等[12]和Tibshirani等[13]考虑了具有L1惩罚的“趋势过滤”; Fearnhead和Maidstone等[14]通过动态规划算法用L0正则化来检测斜率的变化; Spiriti等[15]研究了两种优化最小二乘和惩罚样条中节点位置的算法; Anastasiou和Fryzlewicz提出了ID (Isolation-Detection)方法, 该方法不断地搜索扩展的数据段以检测其中变化, 但正因如此, 会使得某些数据被多次重复计算, 而且每次扩展的数据量只给出一个固定值λ=3, 并没有说明给出的原因, 并且在数据为长时间的小跳跃情况下, 该方法比较乏力。
二元分割方法[16](Binary Segmentation, BS)是多变点检测的经典方法之一, 与其他变点检测方法相比,该方法检测效果很好, 特别是对大量数据, 长期性数据的多变点检测, 很多单变点检测方法都能跟二元分割相结合而转化为多变点检测, 如Olshen A B等[17]的CBS(Circular Binary Segmentation)方法,Fryzlewicz的WBS(Wild Binary Segmentation)方法[18]和WBS2(Wild Binary Segmentation 2)方法等,但这两种方法都是用于检测均值变点, 所以在数据存在异常值时, 检测结果会存在很大偏差。在二元分割方法中, 检验统计量非常重要, 所以在本文中, 根据Baranowski等[19]提出的统计量作为的检验统计量, 同时受到WBS理论对整个数据区域随机“产生”区间以检测变点的启发,也对整个数据序列随机抽取检测区间进行变点检测。
1 模型及检测方法
1.1 模型介绍
在具体应用过程中, 由于数据类型的多样性, 不同的数据, 其分布类型不能确定, 参数方法已经无法满足实际应用的需求, 然而非参数方法对总体分布的假定要求低, 不会因为对总体分布的假定不当而导致重大问题, 更能体现让数据说话的特点, 具有很好的稳健性, 所以基于非参数模型对变点进行研究更具有通用性。
对于观测的数据序列Y=(Y1,Y2,…,YT), 运用如下经典的单变量统计模型:
Yt=ft+σtεt,t=1,2,…,T
(1)
其中,Yt为单次观测数据,ft是确定的数据信号,εt为独立的随机噪声, 且εt~N(0,σt2), 在第二节数值研究设σt=1。假设时间序列数据Y有q个变点, 则Y被分割为q+1个不同的区间段, 记变点的位置分别为0=τ0<τ1<,…,<τq<τq+1=T, 其中q的值和变点位置τ未知, 需要估计, 第i个区间段的数据为Yτi-1+1:τi=(Yτi-1+1,Yτi-1+2,…,Yτi), 本文研究的是分段线性趋势的数据, 所以此处每个区间段的数据呈线性相关, 研究的目的是估计出每个区间段的首尾端点, 也就是变点。
在该模型中, 设σt=σ, 则对σ的估计, 可以运用中位数绝对偏差(Median Absolute Deviation, MAD)方法[20], 在εt为独立同分布的高斯情况下, MAD定义为
其中,Φ-1(·)表示标准正态分布的分位数函数。注意, MAD的估计值对ft中的任何变点都是稳健的, 因为它结合了对差异数据的处理和对中位数的使用。
1.2 检验统计量
检验统计量作为变点识别的主要部分, 其检测能力直接影响变点检测的最终结果,选择一个好的检验统计量至关重要, 所以选择Baranowski在2019年所提出的统计量[19]为本文的检验统计量, 具体构造如下。

对于区间(s,e], 在给定(Ys+1,Ys+2,…,Ye)的情况下, 设l(Ys+1,Ys+2,…,Ye;Θ)为Θ的似然,Θ为参数空间, 则广义对数似然比定义如下:
而对比函数是由数据与对比向量的内积所构成, 定义对比函数为
(2)
(3)
其中,
γ(s,e]=(γ(s,e](1),γ(s,e](2),…,γ(s,e](T))T,
以及常数向量
1(s,e]=1(s,e](1),1(s,e](2),…,1(s,e](T))T,
在向量

1.3 变点检测方法
本文的主要思想是将数据Y=(Y1,Y2,…,YT)的局部与全局处理相结合, 将统计量与二元分割相结合用以检测数据中的多变点, 首先在全局阶段,随机绘制一些子区间(s,e], 此区间的数据为子样本(Ye+1,Ye+2…,Ys), 1≤s 最后,运用强化型施瓦茨信息准则(Strengthened Schwarz Information Criterion, sSIC)对集合S集进行最优筛选, 得出最终变点。 在本节中,根据模型式(1), 产生两组模拟数据以检测本文方法,如图1的两幅图所示,其中波动较大的灰色实线(有噪音)表示所模拟的原始数据Yt,中间的白色实线表示无噪音的分段线性数据ft,与白色实线相近的黑色虚线表示的是根据本文的方法,拟合出来的分段线性数据。从图1中可以明显看出,本文的方法对数据转折点(变点)处的识别很精准,使得运用线性回归来拟合两变点之间数据有着不错的效果,中间的白色实线与黑色虚线几乎重叠。 城市道路的交通状态是交通运行系统中通行能力的体现, 交通流变点就是由于某种变化而导致的, 这种变化有可能是交通事故、自然灾害、交通管控等, 有效及时地分析出交通流的突变情况对提升道路交通的通行能力有很大帮助。 选取深圳市北环大道新洲立交的交通流卡口数据作为研究对象, 以2018-03-17(周六)和2018-03-27日(周二)00∶00—22∶00的数据为例, 每日共660个数据, 对道路卡口每2 min的车流量进行变点检测(数据来源于2018年深圳杯竞赛D题)。 从图2可知, 工作日和周六的数据分布以及变化在某些时段不太一致, 在工作日(周二), 检测出的变点分别为06∶00,07∶08,13∶38,14∶24,16∶44, 对照图2(a), 可以得出在时间段06∶00—07∶08期间, 车流量的增量非常明显, 在13∶38—14∶24时间段, 有短暂的增加, 在16∶44以后, 道路车流量也增加地比较明显, 可以得出, 在工作日, 该道路的早中晚高峰期比较明显, 这与实际情况完全吻合。 在休息日(周六), 检测出的变点分别为06∶00,08∶44,12∶58,14∶42,相比工作日, 变点减少了一个, 而且明显可以看出, 在06∶00—08∶44和12∶58—14∶42这时间段的车流量增长比工作日要缓慢许多,这是由于周末大家都没有上班, 车流量的增长速度相对工作日就比较缓慢, 而在下午却没有晚高峰,由于下午没有下班的高峰期, 所以下午就没有变点的出现。 综上可得, 在工作日和非工作日的交通流量, 在增长速度方面的差异比较大, 工作日的变化情况比较明显, 该方法能很好地检测出交通流中的变化情况, 如果出现了交通事故等问题, 交通流量情况一定会在数据中体现出来, 只需运用此方法就可知道交通中出现的事故等,并且出行人可以合理调整自己的出行时间, 避开出行的高峰期, 交管部门也可根据此实际情况对交通进行有效调控。
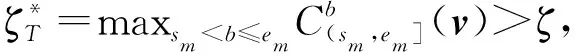
1.4 强化型施瓦茨信息准则
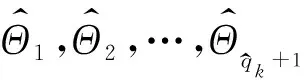
1.5 计算复杂度分析

2 模拟研究
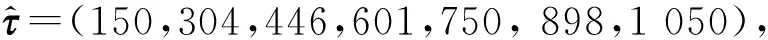
3 实例分析
4 结束语

