高考圆锥曲线解题教学关键——坐标法

北京 白志峰 于艳梅

高考圆锥曲线试题思想方法交汇强，能力要求高.试题通过解题策略的选择、解题障碍的突破区分不同层次的考生，是拉开考生分数档次的关键题目之一.

综观各套高考试题，多以直线与椭圆为载体.试题入口低、观点高，突出考查解析几何的基本知识、基本思想，兼顾对数学思想和数学能力的考查.试题从学科的知识交汇与思想体系去认识、把握解析几何的核心思想——用代数的方法解决几何问题,其核心的解题方法是坐标法.

所谓坐标法，就是建立坐标系，把几何对象转化为代数对象，把几何问题转化为代数问题，利用代数工具、方法研究并获得结论，然后再解释几何对象.

一、圆锥曲线的解题教学方面存在两个不良倾向

其一，刻意地把几何条件的转化当做所谓的“亮点”.有的教师选择一些几何条件复杂、不易转化利用的题目，竭力分析如何巧妙转化，这样虽然能增加教师授课的吸引力，但冲淡了解析几何基本思想的落实.有的教师从几何条件的分析转化出发，列出多种方法，剩下的运算留给学生完成.事实上，几何条件的转化是为坐标法的顺利实施提供支持的.考生在读懂题意方面没有较大障碍，大多能够尽快理清条件信息，找到解题思路.其中，几何条件的转化并不复杂.

其二，过分的模式化训练.多数教师习惯于题型归类、方法总结.比如有的教师从易到难划分题型：位置关系问题、最值与范围问题、定点与定值问题、存在性探索性问题等等，并且进行解题训练.通过各类题目总结许多“解题模式”，这样会给学生带来负面的“条件反射”.事实上，不管何种题型、不论如何变化，最常用的方法是坐标法.

二、落实好坐标法需把握好如下三个问题

第一，教师要善于促使学生形成可行的解题思路并进行有效的变通.

解题思路的形成是解题者根据题目条件提供的信息和结论的目标指向，结合大脑储存的数学知识、思想、方法，共同作用的结果.条件是基础，结论是方向，变通是关键.教学实践表明，学生在解答圆锥曲线综合题时不是没有思路，而是存在以下两个问题：一是解题思路不可行，二是思路可行但变通不畅.找准了问题的关键，也就找到了教学的着力点.所以教学中教师既要善于促使学生形成可行的解题思路，又要善于促使学生形成有效的变换与沟通.

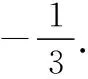
(Ⅰ)求动点P的轨迹方程；

(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，请说明理由.

【解析】(Ⅰ)P的轨迹方程为x2+3y2=4(x≠±1)；

(Ⅱ)第一步：分析题意，形成思路.

可用条件：①P在椭圆x2+3y2=4(x≠±1)上；②直线AP和BP分别与x=3交于点M,N；③S△PAB=S△PMN.

目标指向：P点坐标(若存在).

这里必须明确何为P点存在？何为P点不存在？

设P(x0,y0)，若关于x0(或y0)的方程有解，且x0∈[-2,2]时，则P点存在，否则P点不存在.于是就需要建立关于x0的方程，那么如何建立呢？考虑条件③，面积相等是几何条件，其代数表达如何？思路由此展开.

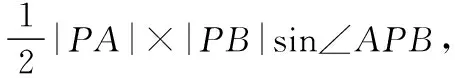
接下来，需将④，⑤坐标化.设点M，N的坐标分别为M(3,yM)，N(3,yN),

由④⟺ 2|x0+y0|=|yM-yN|(3-x0),⑥

由⑤⟺|PM|×|PN|=|PA|×|PB|,⑦

第二步：合理转化，有效变通.

⑥的问题是字母过多,如何减少,这就是变通的问题了.条件②的本质是三点共线,可实现用P点坐标表示M,N的坐标：

法一：利用直线AP与直线x=3求交点M，直线BP与直线x=3求交点N；

法二：利用kAP=kAM，kBP=kBN；

第三步：规范书写，完成解答.

根据以上分析，不难形成多种解题方法，这里略.

只有第一、第二两步处理的合理到位，才能形成有效的解题思路，教师的引导作用的重点应该在第二步，第一步和第三步只要留足一定的时间和空间，学生是能够独立完成的.

有效的解题策略、思路、方法，不是教师告诉学生的，而是学生自己生成的.教师要回避“告诉式”的教学方式.教师的作用是引导学生找到一种正确的、可行的思路，并且经过一段时间的训练成为学生的自发行为.

教学时应该围绕坐标法展开，从不同角度切入，用多种方法解答.既要重视一题多解，又要重视多题一解.通过一题多解开拓思路，通过多题一解把握本质.

第二，教师不能一味引导学生规避运算，要让学生想得出来、算得出来.

数学运算是数学核心素养之一.运算能力包括分析运算条件、探究运算方向、选择运算方法、确定运算程序等一系列过程中的思维能力，也包括在实施运算过程中遇到运算障碍而调整运算的能力.解析几何试题承载着高考对运算能力的考查要求，试题对于运算量的大小、运算长度及运算障碍的设置都是经过慎重考虑的，在整个试卷里是合理配套的，因而运算能力也是考生应该具备的，不可回避的.

【例2】已知抛物线y2=4x，点R(1,2)，过点Q(1,1)作直线交抛物线C于不同两点A，B，若直线AR,BR分别交直线l：y=2x+2于点M，N，求|MN|最小时直线AB的方程.

【解析】教学时，发现一学生给出如下解法片段：

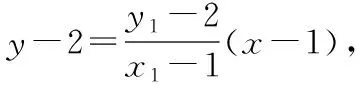
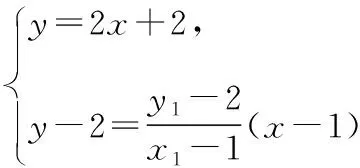
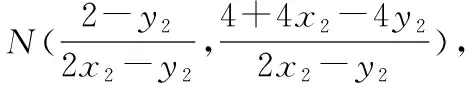
至此停滞不前，怎么办？学生的解题思路何尝不是立足根本，中规中矩的解法呢！而且极具代表性.该生能算到这一步确实不易，说明他的运算很准确，值得肯定与表扬.所以教师不要急于抛出自己的想法，或急于展示其他学生的成功解法.应该顺应该生思路，引导学生共同分析、评价，找出问题，找出方法，让学生在比对与评价中学会处理问题.

停滞不前的原因显然是变量过多.如何减少变量呢？肯定还有一些条件未利用.这个原因一经提出，众生发现：

师：“好！点在曲线上，则点的坐标满足曲线的方程，反之呢”？

生：“点的坐标满足曲线的方程，则该点在曲线上.”

师：“这正是解析几何的基本思想之一.之所以停滞不前，是因为这种意识不强烈.”

教师要抓住这一有利时机，帮助学生强化点在曲线上，则点的坐标满足曲线的方程；反之，点的坐标满足曲线的方程，则点在曲线上，这一解析几何基本思想的理解和认识.此时此刻，学生的思维是活跃的.又有不少学生发现将④代入①②先化简，再解交点更简单.

教师肯定与表扬之后，留出时间让学生做下去，看谁做得又对又快！在最后处理目标函数最值时，又是一个节点，本文不再赘述.

第三， 教师要善于发挥顺势而为的教学价值.

( )

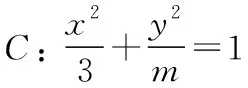
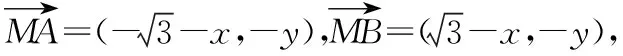
但到此停滞不前，有的放弃，有的“死算” . 难道解法不可行？为什么通法“不通”，“阻”在何处？面对这样的情况，教师该怎么处理？毕竟是学生自己的思路，而且是非常合理的，学生已经避开利用余弦定理求解的途径，说明经过了充分的思考 .教师要善于发挥顺势而为的教学价值.

面对①式怎么办？顺势而为的第一个结点：

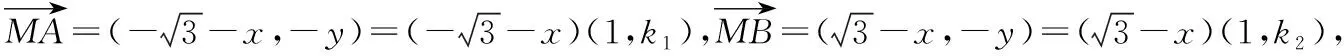
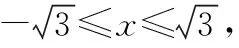
k1,k2有什么关系——顺势而为的第二个结点：

解得m≤1或m≥9，又0

焦点在y轴上时，由学生自己完成，目的是及时巩固以上方法，达到真正理解，起到举一反三的效果. 此时得出结论：m≥9.

当然，我们不一定提倡考场上这样解题，但是在习题课上如此“认死理”的解答，重在解答过程中所经历的体验和学到的东西，培养学生求真务实的科学精神和锲而不舍的意志品格，这正是新版课标中所提倡的必备品格.

本题利用“椭圆短轴端点对两焦点的张角最小”，可以简便求解，这里不再赘述.

课堂上留足时间、空间让学生想出来、做出来，并进行“策略选择、运算方法、障碍调整”等方面的反思、提炼.通过这样的过程可以让学生体验成功的乐趣，树立战胜困难的信心，培养锲而不舍的意志品质.

新一轮课改后的高考改革已见端倪.解析几何综合题依然是高考的热点和重点，必将常考常新，所以难免由陌生之感而产生难度.但无论如何，都不会离开解析几何的学科本质.解题教学的重点是有效的解题思路的形成和运算的顺利进行.说到底就是要：明确一种思想——用代数的方法解决几何问题、强化一种方法——坐标法、树立一种态度——解决问题、培养一种品质——不服输.