Canny算子在PCBA目标边缘提取中的优化应用
李 彦,赵其峰,闫 河*,李晓玲,谢 敏
(1.重庆理工大学 计算机科学与工程学院,重庆 401320;2. 重庆理工大学 两江人工智能学院,重庆 401147)
1 引 言
PCBA元器件边缘检测是自动化生产线智能机器人视觉引导的关键技术,传统canny算子[1]具有较好抗噪与边缘定位能力而广泛应用于PCBA元器件的边缘检测。但由于智能手机PCBA元器件规格尺寸细小、集成密集,且镜头、插槽、芯片、电阻等各元器件光反射特性不同,采集的图像光照非常不均匀,在实际应用中,传统canny算子检测的元器件边缘存在明显的伪轮廓和边缘粘连情况[2],元器件边缘检测的精度不高,难以满足后续的对元器件定位、测量及装配等高精度视觉引导技术的需求。文献[3-4]指出,传统canny算子采用高斯滤波来消除噪声,虽提高了图像的信噪比,但目标边缘过平滑现象突出、边缘细节信息丢失严重,导致最终检测的边缘存在明显的伪轮廓和边缘粘连现象;文献[5]指出,传统canny算子最后一步的双阈值检测易导致目标的边缘断裂,产生过多的伪边缘,进一步加剧了边缘检测的表现力降低。
针对以上传统canny算子存在的问题,曾出现了许多改进算法。文献[6]提出使用区域图引导的双边滤波替代高斯滤波,根据图像区域内噪声属性和区域之间的相似度动态调整滤波系数,在实现滤波的同时可以有效地保持图像的结构信息。该方法在边缘保持方面具有较好的效果,但算法过程复杂,耗时较为严重[7],且降噪效果不理想。文献[8]提出一种梯度幅值直方图和类间方差最大法的自动阈值选取方法,通过将非极大值抑制后的像素点进行分割得到三类像素点,对每类像素点通过类间方差最大化求取最大值,即为三类像素点的分界点,该方法较好界定了区分非边缘像素与边缘像素的分割阈值,但在计算梯度等级时需要根据经验得出,方法的适应性较差[9]。
为避免降噪引入图像模糊的问题,借助引导滤波梯度保持特性,本文提出改进的具有“动态”惩罚项的引导滤波算法(Dynamic Penalty Guided Filtering,DPGF),相对于文献[6]中提到的方法,引导滤波算法本身具有更快的处理速度[10]和较好的边缘保持效果,使用局部动态惩罚项可以有效避免图像的过度平滑或欠平滑问题,相比于区域引导方法,本文具有更精确和灵活的处理范围;无论是双阈值分割还是文献[8]中提到的最优分割算法,其根本思想均是全局分割,为了将分割区域精细到单像素级别,本文使用局部自适应阈值(LATS)替代全局阈值,利用滑动窗口机制计算局部自适应阈值,实边缘像素与非边缘像素的正确分割。从而期望本文的改进算法,能有效保留边缘完整度且能较好抑制伪边缘的产生,同时,在应用于PCBA元器件边缘检测时,能有效减低元器件周密区域边缘缺失和粘连现象的出现,从而能实现元器件轮廓边缘的精确提取,为后续元器件的高精度尺寸测量、高精度定位提供准确的轮廓边缘信息。
2 Canny算法改进
2.1 具有“动态惩罚因子”的引导滤波算法
假设待滤波图像为I,引导图像为P,输出图像为Q。根据文献[10]中给出的算法公式可以得到式(1)所示的线性模型表达式:
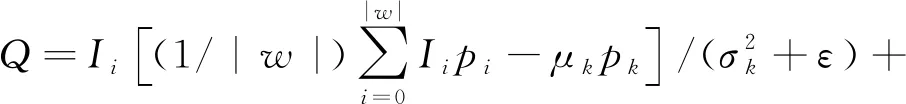
(1)
其中:i,k为像素索引值,μk与σ2分别为邻域块的均值和方差,|w|为邻域块中像素个数,ε为惩罚项。由(1)式分析可知,每个窗口会被持有相同惩罚项的滤波算子多次覆盖,文献[10]以计算均值的方式得到每个窗口最终的处理结果。该方法在一定程度上解决了部分区域平滑不足的缺陷,但由于每个窗口中存在的边缘点数目不同,而处理过程使用相同的惩罚项,对于边缘稀疏区域存在过度平滑的问题。
针对引导滤波算法使用全局惩罚项带来的上述问题,本文利用窗口内边缘点的数目作为判定依据,引入新的阈值惩罚项β,权衡边缘稀疏和边缘丰富区域的滤波效果。改进后的算法为:
Qi=βQi(β∈(0,1]),
(2)
(3)
β=s/|w|,
(4)
其中:T表示类间方差最优阈值,用来表示像素块中边缘点的丰富程度,s表示窗口内超过变化阈值的像素个数,β为像素块内阈值变化比,即“动态”惩罚因子。通过算法改进,在像素块中边缘像素点较多时会获得较大的惩罚因子,反之,惩罚项随之减小,解决了全局惩罚因子造成局部滤波不均的问题。
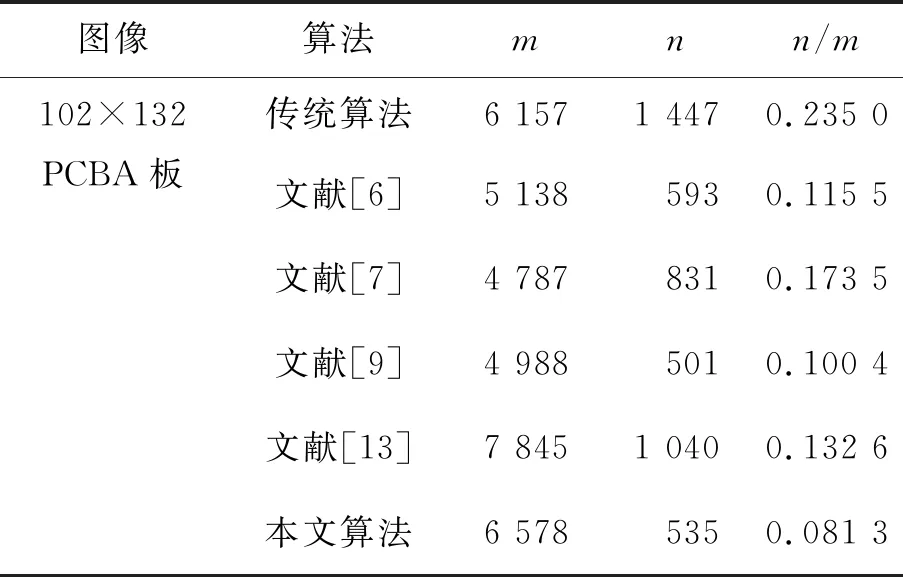
本文使用基于误差敏感的峰值信噪比(Peak Signal to Noise Radio,PSNR)和基于亮度(均值)、对比度(方差)、结构三个层次评价图像失真效果的结构相似度(Structural Similartiy,SSIM)[11-12]两指标衡量改进后算法的执行效果。如表1,通过使用局部动态惩罚因子改进后的算法,滤波效果较文献[6],文献[7]和文献[13]有较大提升,说明图像中噪声得到很好的抑制,具体体现在本文PSNR有较好的数值表现。为了避免单一指标存在误差,文本对滤波前后的两幅图像进行结构相似度度量,由表1可知,本文算法结构相似性达到0.998 7,该数据[13]说明滤波后的图像细节得到最大程度的保留。
由于篇幅有限,本节只对手机PCBA电路板图像灰度等级直方图进行分析,如图1所示,图1(b)为传统canny算子高斯滤波处理的结果,区域1部分峰值较高且位于中间部分,表明图像整体对比度偏低,图像区域1和2两部分较图1(a)部分差值较大,表明算法对图像具有增强作用,但整体缺乏稳定性,破坏了图像中的原本的梯度结构信息,这与引言部分分析一致,也是目前信噪比虽然可能被提升,但图像质量却下降的主要原因。图1(c)区域1波峰部分较图1(a)和1(b)两图增强明显,区域2部分较图1(a)增强稳定,主要原因是PCBA电子元件密集且主要为黑色,图像亮度差异较小,双边滤波固有的特性是在灰度差异较小的部分使用高斯滤波进行处理,所以其灰度特征与图1(b)相似,但增强幅度不同。图1(d)区域1和2两部分,较图1(b)中,差值较小,但较图1(a)梯度特征差异较大,区域2部分出现大量高频噪点,与文中使用的快速双边滤波的特性有关。图1(e)同样使用高斯滤波,但与图1(b)~1(d)不同的是,图1(e)算法通过建立高斯尺度空间进行采样,2区域中增强稳定,但1区域增强过大,加剧了图像的对比度差值,偏离了原图像梯度特征。图1(f)中由于将双边滤波和引导滤波进行结合,整体梯度特性得到保持,但由于引导滤波中全局惩罚项的缺点,导致梯度增强不明显,部分区域有过平滑现象,具体表现为区域2部分较图1(a)更加平缓。图1(g)为本文使用“动态”惩罚引导滤波算法处理得到的结果,较图1(a)中梯度得到增强,且整体增强稳定,没有出现大范围的梯度剧变问题,在梯度保持的情况下增强了边缘与背景的差异度,有利于实现两者的分离。
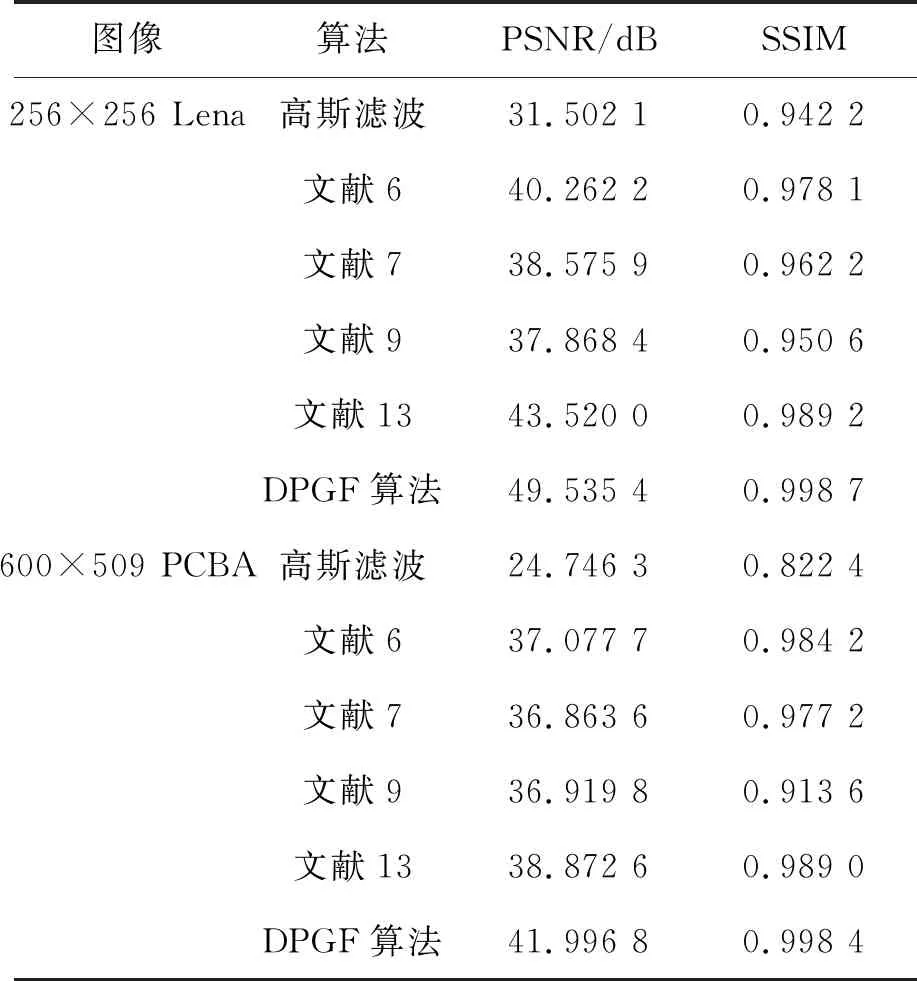
表1 改进算法结果比较
通过对PCBA图像梯度直方图分析可以发现,文献[13]算法在处理边缘稠密,灰度差异较小的图像时具有良好的降噪和梯度保持效果,而文献[6]与文献[7]和[9]正好相反。本节提出的具有“局部动态惩罚因子”的引导滤波算法在降噪的同时因为使用梯度引导图像,同时具有良好的梯度保持效果,在保边去噪方面表现良好。
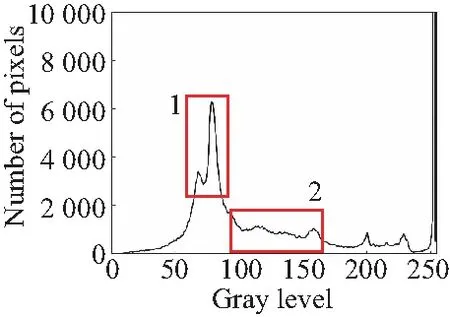
(a)原图像(a)Original image
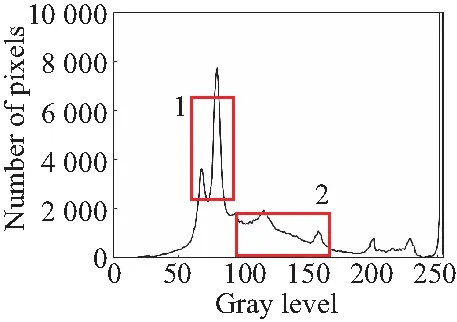
(b)高斯滤波图像(b)Gaussian filtered image
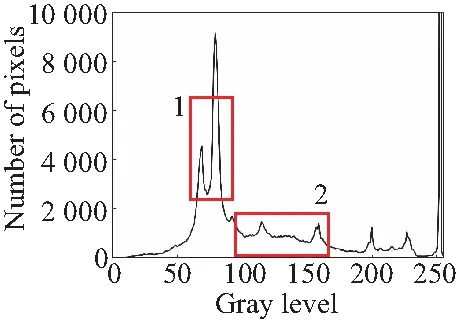
(c)文献[6](c)Literature [6]
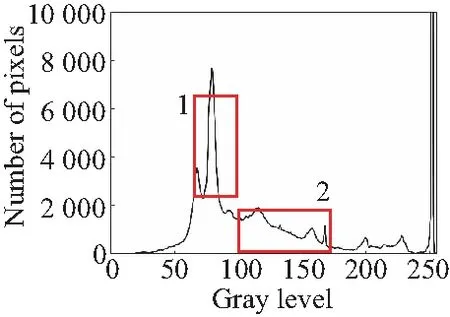
(d)文献[7](d)Literature [7]
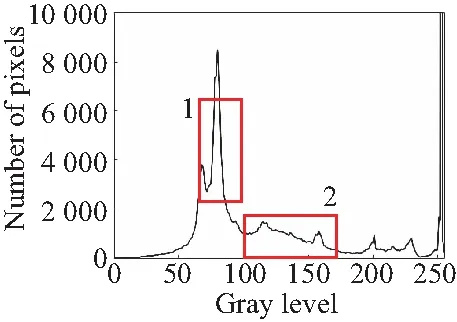
(e)文献[9](e)Literature [9]
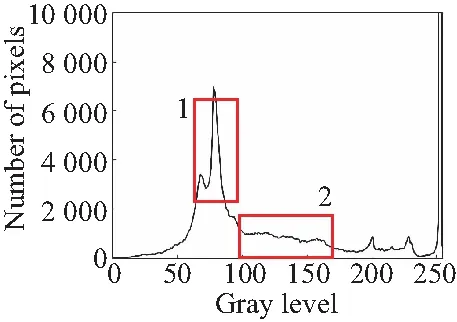
(f)文献[13](f)Literature [13]
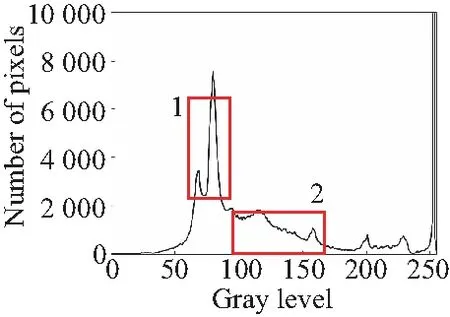
(g)DPGF算法(g)DPGF algorithm图1 PCBA灰度直方图Fig.1 PCBA grayscale histogram
2.2 局部自适应阈值分割算法
手机PCBA电路板元件稠密,规格较小,各元件对光源反射程度不同,导致工业相机采集图像存在明暗的细微差别。传统canny算子通过人工设置全局阈值完成像素点的分割,对边缘丰富,目标较小的区域边缘检测效果较差,边缘粘合情况严重。为了尽可能保留光源反射较差区域的边缘细节,本文受文献[9]中梯度幅值直方图和类间方差最大法启发,使用改进的局部自适应类间差分法提高局部阈值分割的有效性,避免因元件光学特性造成局部较暗而设定阈值较高出现大量边缘丢失和粘合的情况。
设像素块中像素的灰度范围为[T1,T2],每个灰度g对应的像素点个数为Ng,像素块大小为,则每个灰度级占比像素的块的概率可以由式(5)得出:
Pg=Ng/N,∑Pi=1(i∈[T1,T2]).
(5)
此时,对像素块中背景灰度级gb(b∈[T1,T])和目标灰度级go(o∈[T+1,T2])求取期望值E,如式(6)所示:
E=∑gPb(b∈[T1,T2]),
Eb=∑gbPb(b∈[T1,T]),
Eo=∑goPo(o∈[T+1,T2]).
(6)
为了得到最优的局部分割阈值,可以使用线性回归思想,求取类间方差的极大值,如式(7)所示:
σ2=(Eb-E)2+(Eo-E)2.
(7)
对σ2求得最大值记为本像素块的局部最优阈值,为了保证良好的分离特性,设像素块求得最大阈值为Th,容差为Tc则分离判定条件如式(8)所示:
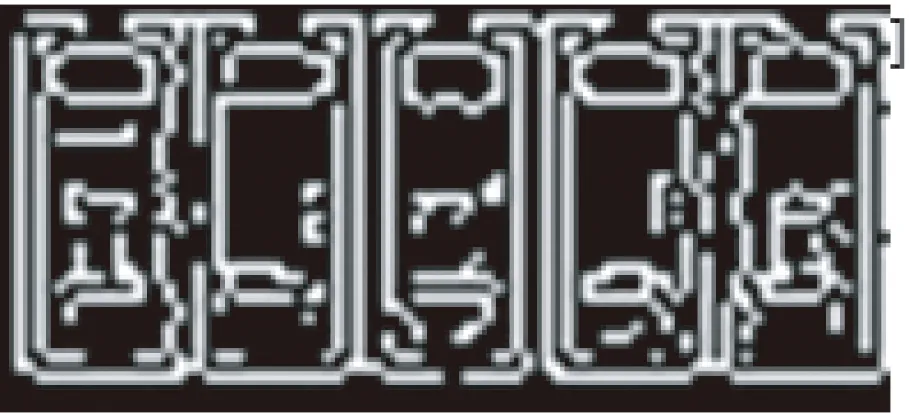
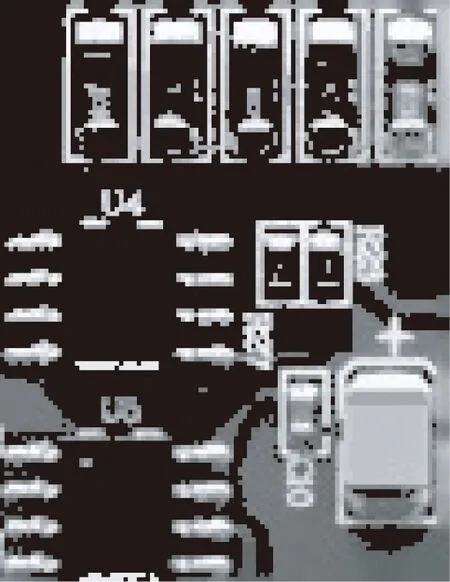
Pi=Pi*θ(Pi (8) 其中:Tc为常数值,需人为设定值,本文选取7得到最佳阈值分割效果。θ为像素值衰减比例,范围介于0~1之间,图片不同,取值不同。P为像素块中8邻域像素总和。 以手机PCBA电路板局部放大图像为例,图像未经任何滤波操作。本节仅选取2.1节中数据表现较好的文献[13]以及针对阈值分割进行改进的文献[9]进行实验对比,对于其它文献由于在本章节使用方法不同,在此不做对比。如图2,图2(b)区域1部分,使用阈值分割的效果较好,除部分边缘噪点外,整体轮廓清晰,区域2部分,由于元件与背景灰度差值较小,受背景刻线影响,分割效果不明显,出现大量伪边缘,表明算法缺乏对背景复杂情况下灰度差值较小区域的有效处理。图2(c)区域1部分,检测效果较差,出现区域粘合,区域2部分,检测效果较好,但出现目标边缘缺失现象,对灰度差值较小区域,分割仍然不敏感,表明算法对背景干扰刻线具有较好的屏蔽效果,但存在边缘丢失现象,在边缘密集区域,分割效果较差。图(2)d在区域1部分,对边缘密集区域分割较为,明显,没有出现边缘粘合现象,区域2部分对背景中存在干扰的刻线具有较好的屏蔽效果,整体检测效果均好于前两种算法。 (a)原图(a)Original image (b)文献[9](b)Reference [9] (c)文献[13](c)Reference [13] (d)LATS方法(d)LATS algorithm 图2 局部自适应分割图Fig.2 Local adaptive segmentation map 本文对手机电路板不同区域进行边缘检测,通过观察对局部光线变化频繁且边缘丰富区域的提取效果来验证算法的有效性。 本文所有实验改进结果均借助VS2017和Pycharm仿真平台进行计算验证,实验图像借助实验室内模拟手机工业生产线搭建的移动平台进行采集。图3为各种算法对PCBA电路板图像边缘检测效果。图4为不同窗口大小下,背景的抑制效果。 图3为多电阻并排区域放大图,图3(a)中,图像边缘检测混乱,出现较多的干扰点,未能将电阻边缘进行独立的分割,出现边缘粘合问题,与引言部分分析一致,表明算法在降噪过程中不彻底。图3(b)出现大量边缘断裂情况,整体的分割较差,该算法仅在执行速度上进行了优化,算法本身仍然保留了双边滤波算法的缺点,与本文前面分析结果相符。图3(c)算法,对背景估计,利用高斯金字塔实现复杂背景的消除,该算法对图像光照不均(主要由元件反光导致),背景复杂,且差异较小的图像处理效果不理想,图中虽然对各个元件之间进行了分割,较图3(a)、3(b)效果较好,但仍然因为背景的干扰出现边缘粘连现象。图3(d)算法,虽然在整体数据表现上较好,但在边缘密集,背景复杂区域的分割效果较差,但整体的轮廓位置较为清晰。图3(e)为本文算法的处理结果,虽然元件内部检测不完整,但元件的边缘检测效果较好,在图中除一条边缘发生粘连情况外,其他元件边缘独立,表明算法对边缘密集、背景复杂、光照不均情况下,PCBA元件边缘检测具有较好的实验效果。 图4为本文算法选用不同大小窗口对背景进行处理的效果,从图4(a)~4(c)不断增大窗口过程中,背景颜色逐渐变为全黑,干扰点的数量急剧减少,到图4(d)时除元件本身外,背景颜色变为全黑色,干扰点的数量降到最低。在图4(d)~4(f)窗口不算增大过程中,背景刻线以及白色干扰点开始逐渐增多,处理效果变差,因此本文在处理背景干扰的问题时,滑动窗口选择为19所得到的效果最佳。 为更加直观测试算法的执行效果,利用文献[14]中提出的一种边缘检测量化方法,m表示边缘点的数量,n表示满足3×3 pixel块中单连通条件的像素数,n与m的比值表示边缘连接的完整度,比值越小表示边缘连接的完整性越高。本文算法与文献[6-7],文献[9,13]以及传统算法进行比较,结果如表2所示,其中文献[6,9]算法的边缘完整度近似,表现效果与本文前面分析一致,传统方法表现最差,得到的边缘效果远远低于各文献改进后的算法,文献[7,13]整体表现较差,其主要原因与选取的检测部位有关,对边缘密集区域的边缘检测能力较弱。 (a)文献[6](a)Literature [6] (b)文献[7](a)Literature [7] (c)文献[9](c)Literature [9] (d)文献[13](d)Literature [13] (e)本文算法 (a)7×7窗口(a)7×7 window (b)11×11窗口(b)11×11 window (c)17×17窗口(c)17×17 window (d)19×19窗口(d)19×19 window (e)25×25窗口(e)25×25 window (f)80×80窗口(f)80×80 window图4 不同窗口大小对背景的屏蔽效果Fig.4 Shielding effect of different window sizes on the background 本文算法较其他算法得到的完整度最高,较其他文献中表现最好的文献[9]边缘检测完整度提高了23%,表明本文算法对手机PCBA板元器件边缘检测有较好的处理效果。 表2 边缘完整度评价 边缘检测在机器视觉领域一直占据重要地位,本文对传统canny算法内容进行改进,对保变去噪能力较好的引导滤波加入“动态”惩罚因子替代高斯滤波,同时使用局部自适应阈值完成像素点的分割。实验结果表明,图像除噪后峰值信噪比较之前提高了0.5~0.6,结构相似性达到0.99,算法边缘保持效果大大提高;手机PCBA电路板元件稠密区域分割明显,表明本文算法对解决光源充足情况下,环形光源与环形漫反射光源均无法克服元件反光差异而导致图像中灰度变化,目标区域与背景差值较小而产生的边缘粘合问题具有良好的实验效果。由于本文算法整体耗时比传统canny算法和文献中提到的部分算法较高,需要进一步优化算法的执行效率,这也是以后需要改进的方向。
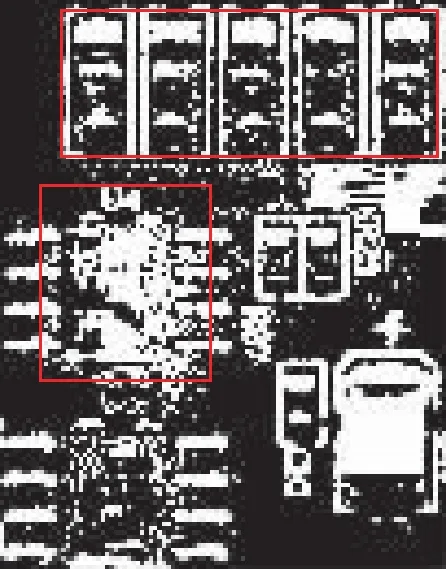
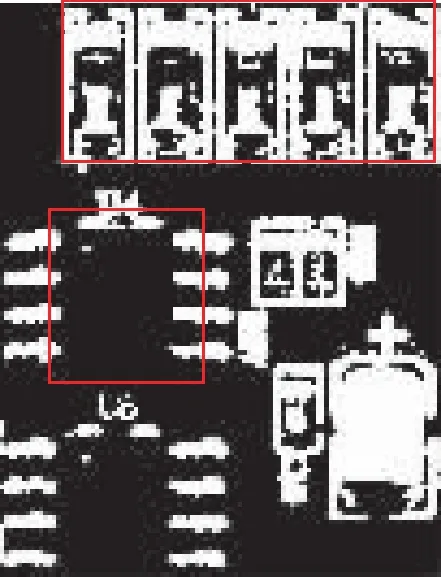
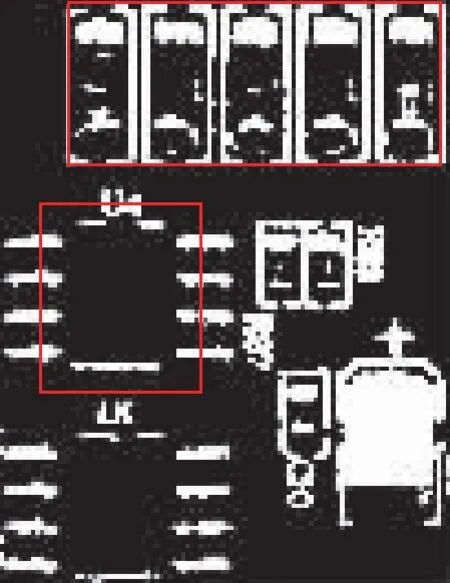
3 实验结果与分析









4 结 论

