低轨高分辨率遥感卫星姿态机动对月定标方法

朱 军，李永昌*，白照广，陆春玲，付凯林，茅歆白，张 璐

(1.航天东方红卫星有限公司，北京 100094；2.国家卫星气象中心，北京 100081)

1 引 言

遥感卫星在发射入轨后，由于发射过程中仪器受到冲击振动以及在轨工作环境发生变化，定标参数会偏离发射前实验室定标结果。为了监测在轨探测器定标参数的变化情况，必须开展遥感卫星的在轨定标工作。传统光学遥感卫星的在轨定标方法主要包括：以定标器为参考源的星上定标、以沙漠、海洋等地物目标为参考源的替代定标、及以定标精度更高的卫星为参考源的交叉定标。然而，星上定标使卫星设计复杂化，并因其本身性能衰减会带来定标误差；替代定标以典型地物目标为参考源，会受地球大气的影响，较难评估大气参数不确定性对结果的影响[1]；卫星间交叉定标需要考虑并修正通道的光谱响应差异，同时由于探测器间通道设置功能的差异，某些通道无法找到合适的参考标准。随着遥感卫星产品逐步走向定量应用，对遥感卫星的在轨定标提出了更高的一致性和稳定性要求，因此迫切需要新的定标源和定标技术来满足这一需求。

月球作为地球的天然卫星，被认为是理想的定标源。第一，虽然月球表面亮度不均，但在太阳、月球、观测点之间几何位置确定的条件下，月球表面具有非常高的光度稳定性，年变化量仅为10-8[2-3]；第二，月球光谱和地物光谱非常相似，其动态范围也涵盖了大地和海洋，且具有不依赖地面定标场、不受天气影响等优势[4]；第三，月球可被任何地球轨道卫星观测到，它提供了一种交叉定标途径，保证了定标的一致性与稳定性[5]。因此，利用月球进行卫星在轨定标是提高辐射定标效率，监测遥感卫星探测器成像稳定性的重要手段。

针对天基对月定标技术，近年来国内外学者进行了大量研究。1993年，美国的SeaWiFS团队首次提出了“月球定标”的概念，在近30年间以月球作为在轨定标源逐渐发展成为一种新的趋势[6]。目前，许多光学遥感卫星，如MODIS[7]、SeaWiFS[8]、Pleiades[9]、GOES[10]以及风云三号卫星的MERSI[11]等均具备在轨对月定标能力，并且欧洲TRUTHS定标星和美国CLARREO定标星将月球选作交叉传递基准[5]。卫星在轨对月定标模式分为两种：一种是被动式，即月球随着轨道运动随机进入探测器的观测视场或冷空视场，几乎所有静止轨道和极轨卫星均采用该模式定标；另一种是主动式，即当需要对月定标时，卫星主动进行姿态机动或载荷摆镜指向跟踪，调整探测器视场指向月球进行定标成像。主动式较被动式具有更高的定标效率，MODIS卫星采用主动对月定标模式，并获取了大量观测数据。近年来，我国开展的在轨对月定标应用多是针对静止轨道和极轨气象卫星，利用低轨高分辨率遥感卫星开展姿态机动对月定标还是一个空白领域[12-13]。

本文提出了一种低轨遥感卫星姿态机动对月定标方法，分析了对月定标时机、对月定标卫星姿态以及载荷成像参数等关键指标，并将研究成果应用于某在轨运行的低轨高分辨率遥感卫星，验证了本文提出定标方法的正确性及合理性。该方法为长期监测遥感卫星探测器稳定性和后续建立中国月球辐射模型提供了数据支撑。

2 对月定标关键技术

2.1 太阳、月球、卫星位置关系

实现卫星对月定标的前提是计算出太阳、月球和卫星间的位置关系。本文采用平均椭圆轨道根数法分别计算太阳、月球矢量。太阳轨道六要素在J2000地心赤道惯性系下可表示为：

(1)

月球轨道六要素在J2000地心平黄道惯性系下可表示为：

(2)

式中：T的单位是儒略世纪，d的单位是地球日。

太阳、月球的矢量表达式分别为：

(3)

(4)

卫星的绝对轨道动力学模型建立在J2000地心赤道惯性坐标系下，设卫星在J2000系下的位置和速度矢量分别为：

r=[rx，ry，rz]T，

(5)

(6)

则卫星在轨道上的运动满足：

(7)

其中fE为作用在卫星上外力之和。

考虑地球非球形摄动带谐项至J4项，地球的势函数为：

(8)

其中：φ为卫星与地心连线在地球表面交点的纬度，r为地心距；μ为地心引力常数，μ=3.986×105km3/s2，RE为地球赤道半径，RE=6 378.136 3 km。地球摄动带谐系数：J2=1.082 6×10-3，J3=-2.536×10-6，J4=-1.623 3×10-6。

则卫星受到的引力为：

fE=-gradU(r).

(9)

若已知卫星在初始时刻的轨道信息，则可通过数值积分完全确定它在任意时刻的轨道信息。在得到太阳、月球和卫星位置在惯性坐标系的坐标后，就可以利用坐标变换和几何关系计算出太阳、月球在卫星本体坐标系下的坐标。

2.2 对月定标时机

在一个月的周期中，月球绕地球运动，使月球、太阳及卫星三者间的相对位置有规律地变化。月相角定义为观测点(卫星载荷)和月球连线与月球和太阳连线所成的角度，如图1所示。一般记满月前月相角为负值，满月后月相角为正值[14]，即上弦月的月相角为-90°，下弦月的月相角为+90°，而满月的月相角则接近0°。

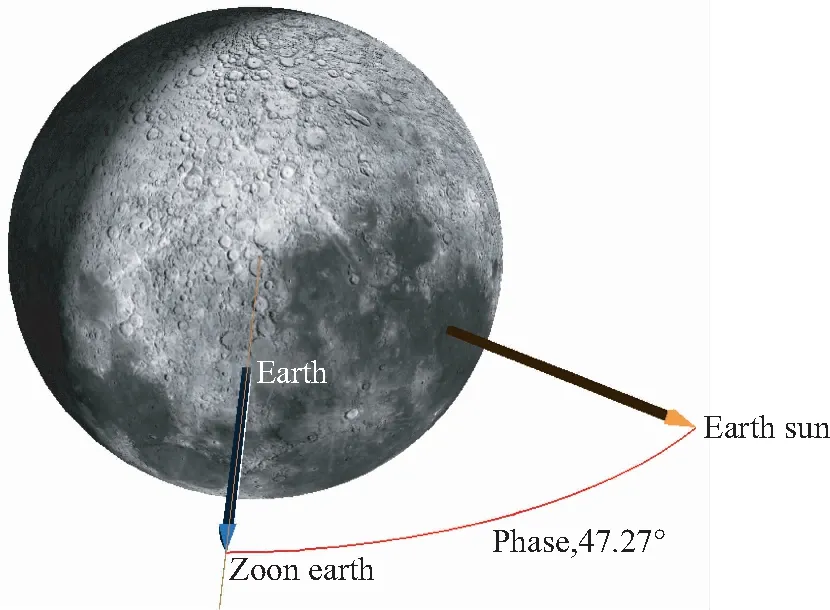
图1 月相角Fig.1 Lunar phase angle

卫星对月定标的载荷成像时机一般选取月面大于50%的情况，即月相角由-90°(初八)至+90°(廿二)的变化期间。同时，为了避免反冲效应(月球表面在0°月相角附近的辐照度表现出一个强烈的后向散射增强效应)，应尽量避开在0°月相角附近定标[15]。太阳同步轨道遥感卫星具备多月相、多位置的对月定标能力，每天运行13～14轨，每轨分别在地球南、北极附近各有一个定标观测窗口，图2为在南极附近的定标示意图。

在此基础上，结合当天卫星测控计划、对地成像任务计划、卫星能源情况和星敏可用情况等因素，综合选取对月定标的载荷成像时机(视轴指向月心时刻)。图3中蓝色线段表示卫星与太阳的可见性仿真窗口，红色线段表示卫星与月球的可见性仿真窗口，其他颜色线段表示卫星与各测控地面站的可见性仿真窗口(彩图见期刊电子版)。对月定标时机的选取应参考图3中的仿真结果，同时需考虑预留定标前的卫星指令上注时间以及定标结束后的卫星健康状态检查时间。

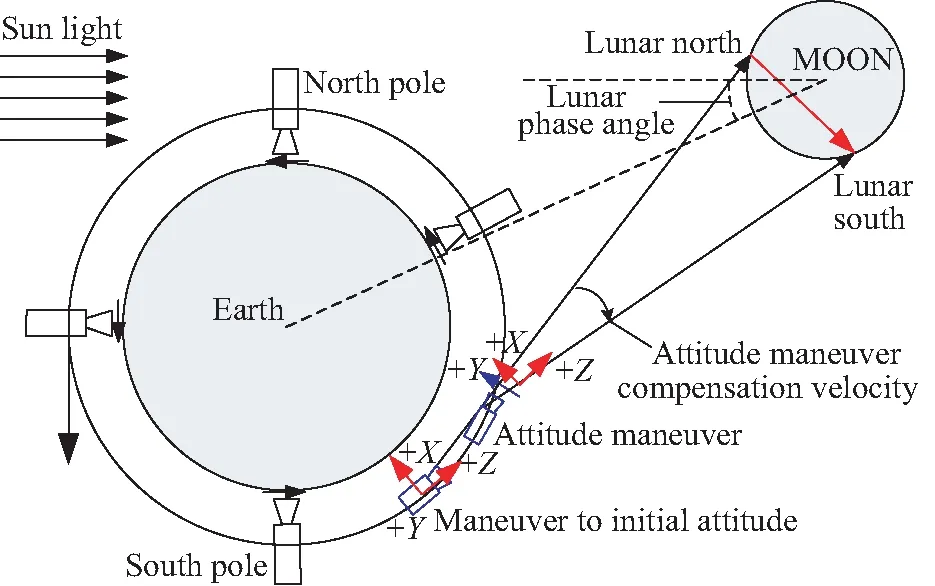
图2 南极附近对月定标示意图Fig.2 Lunar calibration nearby Antarctica

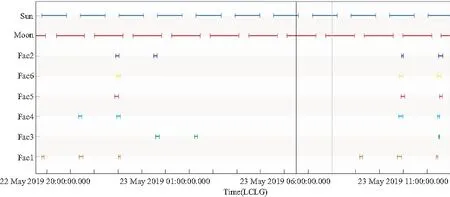
图3 卫星与太阳、月球和测控地面站的可见性仿真Fig.3 Simulation of satellite with the sun，moon and tt&c ground stations

此外，为了保证对月定标期间的卫星姿态控制精度，考虑100 km大气的情况下，需尽量避免杂光进入星敏视场，至少保证两台星敏感器可用。

2.3 对月定标卫星姿态

定义对月定标目标坐标系Os-xtytzt：原点在卫星质心Os处，Oszt轴指向需要观测的目标，Oszt轴与月球轨道坐标系的xmoon轴的叉乘为目标坐标系的Osyt轴，Osxt轴与Osyt轴、Oszt轴构成右手坐标系。根据目标坐标系定义，有：

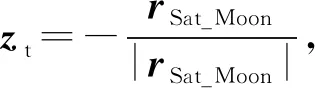
(10)

目标坐标系相对于惯性系的转换矩阵(COT)即为对月定标时机下的卫星指向月心的姿态。将其转换为四元数形式(η，ε)，即有：

(11)

根据上述推导，在计算得到了定标时机、定标姿态等信息的基础上，本文设计了低轨遥感卫星在轨对月定标姿态规划流程，如图4所示。

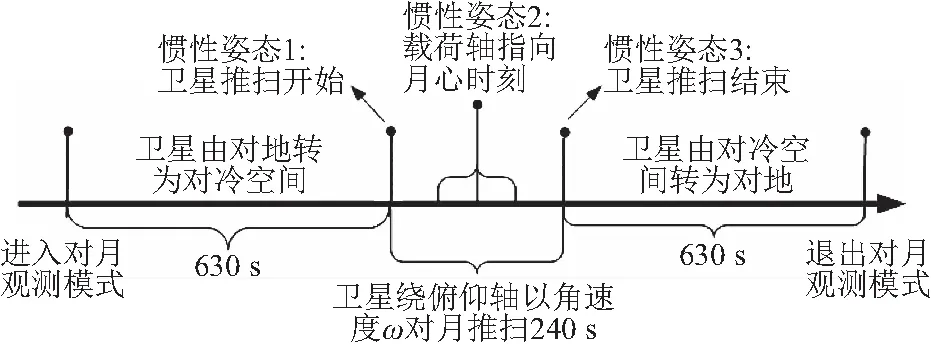
图4 对月定标流程Fig.4 Flow of lunar calibration

首先，将定标时机、定标姿态(惯性姿态2)等信息以程控指令块的形式通过地面测控系统上注至卫星星务分系统。当运行到惯性姿态2时刻之前750 s时，卫星进入对月定标模式，卫星在630 s内逐渐由对地指向转为对月球北侧的冷空间指向；然后在惯性姿态1时刻，卫星开始绕本体系俯仰轴以角速度ωsat对月姿态机动，使载荷的视轴指向由月球北侧推扫至月球南侧；在卫星对月姿态机动的240 s内，载荷在中间的120 s内开机对月成像；随后在惯性姿态3时刻，卫星结束绕本体系俯仰轴姿态机动，并在630 s内逐渐由对月球南侧冷空间指向转为对地指向；最后卫星退出对月定标模式，转入对地姿态。整个对月定标模式共耗时1 500 s，由于成像位置在地球南、北极附近，因此本文提出的对月定标流程几乎不会影响低轨遥感卫星正常的对地观测任务，具有很高的观测效率。图5为卫星对月定标过程中，在惯性姿态1，2，3时刻的STK仿真效果。

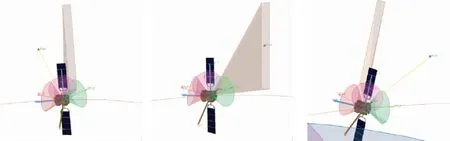
(a)惯性姿态1(a)Satellite attitude 1

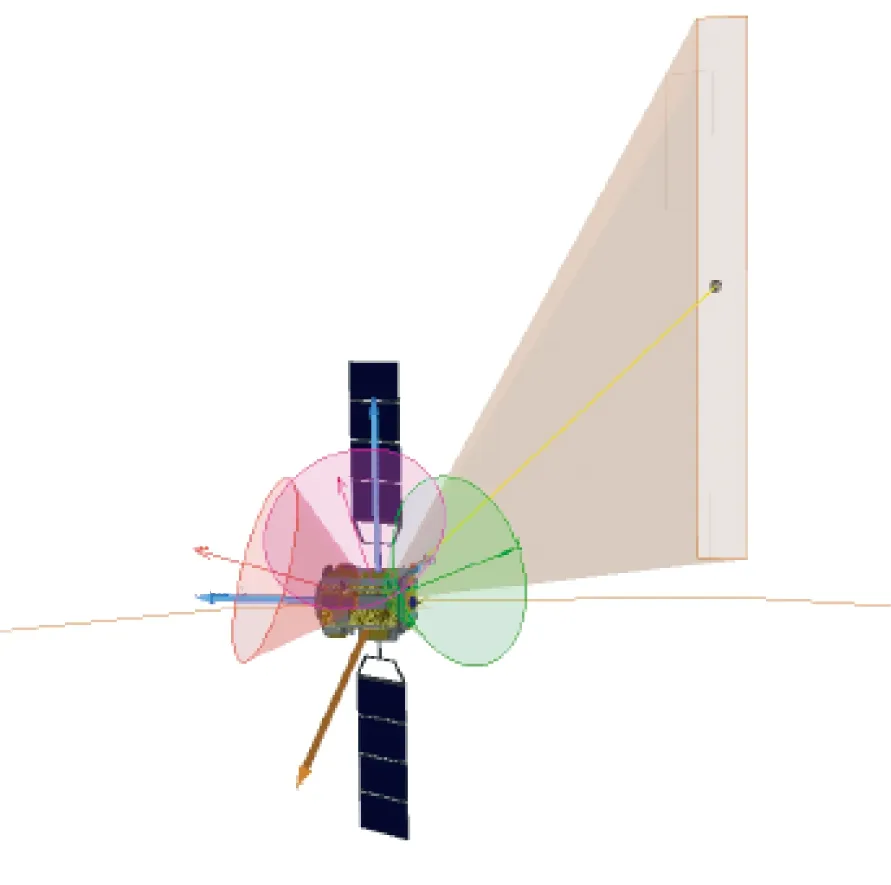
(b)惯性姿态2(b)Satellite attitude 2

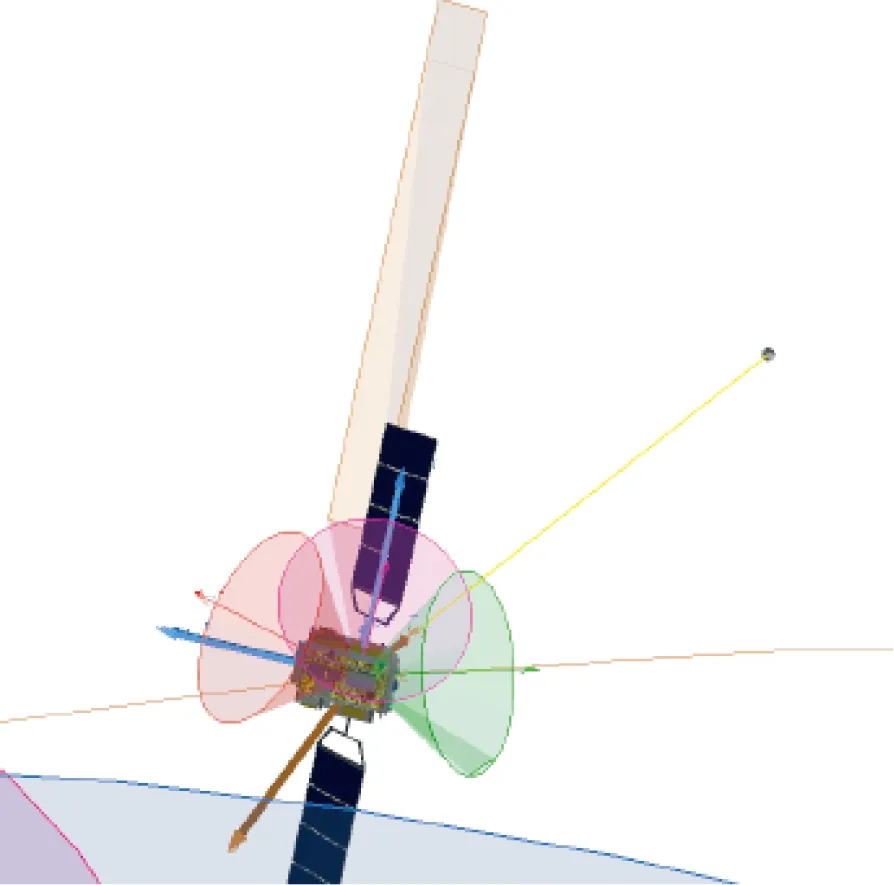
(c)惯性姿态3(c)Satellite attitude 3图5 对月定标流程中的卫星姿态Fig.5 Satellite attitudes in lunar calibration

2.4 载荷成像参数选取

有别于低轨遥感卫星的对地观测，由于观测点与月球距离较远，因此不能直接采用对地观测的成像参数来进行对月定标，所以载荷成像参数的选取是决定对月观测质量的重要因素。

2.4.1 载荷视轴指向

在进行对月观测过程中，载荷视轴由北向南扫过月面，满月时月球所占视场角为：

(12)

其中：Rmoon为月球直径，Lmoon为卫星与月球的距离。

高分辨率遥感卫星的载荷视场角通常大于1°，因此为保证对月定标期间月球能够完整出现在载荷视场内，对卫星姿态指向精度的要求为≤0.2°，这对于高分辨率光学遥感卫星来说不难实现。对于焦面由多片探测器拼接而成的载荷，如要采用固定的某一片探测器进行对月定标，则只需按照该片探测器中心像元的指向角进行对月姿态控制即可。

针对采用时间延迟积分电荷耦合器件(TDICCD)的卫星载荷，需要注意的一点是，月球公转速度约为1 km/s，卫星在轨道上的运行速度约为7.1 km/s。对月定标时需调整卫星姿态，使月球相对卫星的速度在卫星俯仰轴(探测器线阵方向)上的投影分量最小，从而保证成像时二者相对运动造成的横向像移最小。二者的相对运动速度投影在卫星偏航轴方向的分量不会形成像移，而在卫星滚动轴上的分量则会形成TDI积分方向的前向像移，可通过积分时间匹配的手段进行像移补偿，从而实现最好的对月定标成像效果。

2.4.2 载荷积分时间

TDICCD是一种面阵结构、线阵输出的CCD，具有多重级数迟积分、输出信噪比高、探测灵敏度高、曝光时间可控等成像特点。它能够在低照度条件下清晰成像，并且对空间成像环境的适应性非常强，因此目前在轨的高分辨率遥感卫星通常都采用TDICCD作为载荷焦面器件[16-17]。

积分时间为探测器内光生电荷包由上一级转移到下一级所需要的时间。为了避免像移对成像质量的影响，高分辨率遥感卫星通常需要根据摄影点速高比(由GPS接收的姿态广播数据解算)实时匹配载荷的积分时间。由上述分析可知，月球对探测器的视场较小，导致载荷探测器扫过月球的时间非常短，因此本文提出一种过采样系数可调的固定积分时间匹配方法，式(13)为对月定标期间载荷积分时间的计算方法：

(13)

其中：IFOV为载荷的瞬时视场角，ωsat为卫星绕本体系俯仰轴的姿态角速度，k为过采样系数，可根据实际情况调整对月定标的采样比。

2.4.3 载荷积分级数

积分级数为TDICCD电荷包延迟积分的转移次数，适当地提高积分级数，可提升图像的信号强度以及信噪比，但积分级数设置过高会导致图像饱和，高分辨率遥感卫星通常情况下采用16级或者24级进行对地成像。然而对月定标的情况有所不同，首先月球处于冷空间背景中，因此不需设置过高的积分级数也能获得较高的图像对比度；其次，由于对月定标过程中卫星对地成像的偏流角修正功能不再适用，因此过高的积分级数会导致电荷包转移路径增加，从而产生像移，使图像模糊不清。

从调制传递函数(Modulation Transfer Function，MTF)的角度分析也可得出同样的结论，式(14)和式(15)分别为奈奎斯特(Nyquist)空间频率下偏流角匹配误差对MTF的影响以及姿态稳定度对MTF的影响：

MTF偏流角=sinc(N/2·tan Δβ)，

(14)

MTFzt=e-2π2(Δω·f·N·Tint_moon)2υ2，

(15)

其中：N为载荷积分级数，Δβ为偏流角匹配误差，Δω为卫星姿态稳定度，υ为空间频率。可见，当偏流角匹配误差和姿态稳定度一定的情况下，增加载荷的积分级数会导致图像的MTF降低。

为保证高分辨率遥感卫星的成像质量，通常要求由姿态稳定度在N级积分后产生的总位移不大于0.5个像元。依据本文选取的载荷成像参数，推导出了不同积分级数下允许的姿态稳定度指标要求，如表1所示。

表1 积分级数对应的姿态稳定度

综合上述分析，当卫星姿态稳定度优于5×10-4(°)/s的情况下，本文建议采用6级积分级数进行在轨对月定标。

3 对月定标实验

3.1 实验条件

2019年7月10日(初八)至25日(廿三)期间，依据本文提出的对月定标方法，基于某在轨运行的低轨遥感卫星，开展了15次对月球多月相角定标实验。卫星轨道高度为650 km，轨道倾角为97.95°，载荷焦面由6片TDICCD拼接组成，每片CCD的有效像元数为8 192，焦距为3 250 mm，像元尺寸为10 μm。光谱范围覆盖全色(P：0.45～0.90 μm)和多光谱(B1：0.45～0.52 μm/ B2：0.52～0.60 μm/B3：0.63～0.69 μm/B4：0.76～0.90 μm)，载荷对地成像全色空间分辨率优于2 m。综合考虑卫星姿态的机动能力以及载荷积分时间上限等因素，本实验过采样系数设定为10，对月定标期间卫星绕俯仰轴的姿态角速度设定为0.06 (°)/s，载荷积分时间设定为0.293 8 ms。具体对月定标实验信息如表2所示。

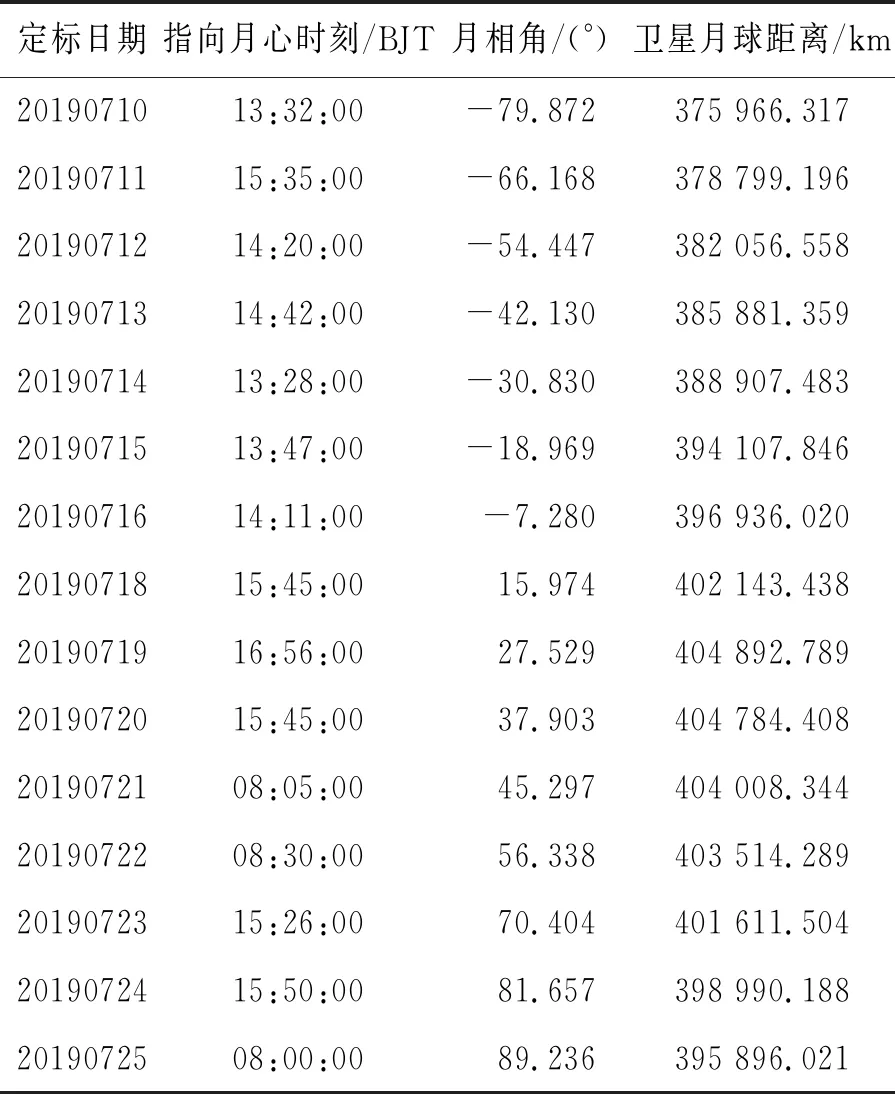
表2 对月定标实验信息

3.2 实验分析

对月定标实验的月相角分布如图6所示，月相角由7月10日(初八)的-79.872°逐渐减小到7月16日(初十四)的-7.280°，再逐渐增大至7月26日(廿三)的89.236°，实验对7月份月面大于50%的情况进行了多月相角定标。

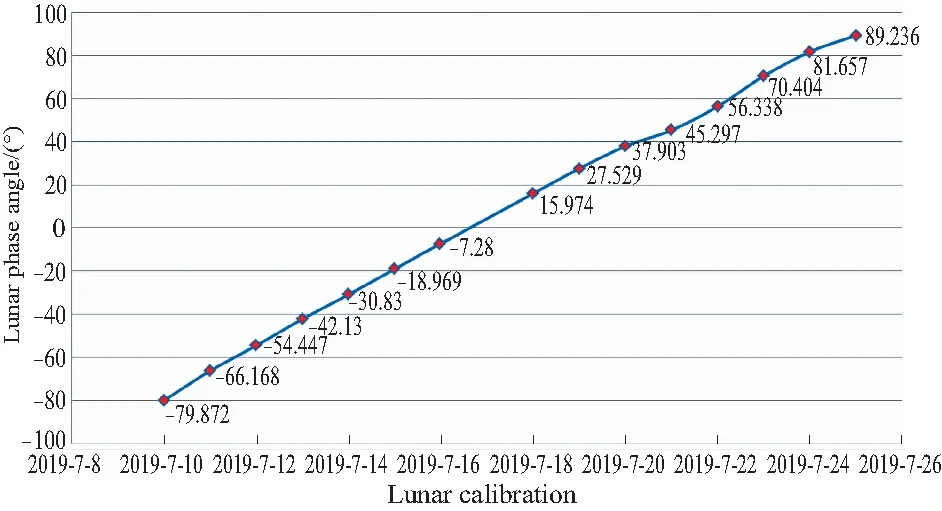
图6 对月定标实验月相角分布Fig.6 Distribution of lunar phase angle in lunar calibration experiment

以7月10日对月定标实验为例，分析对月定标过程中星敏感器的可用情况。星敏指向与太阳和地气光夹角遥测数据如图7所示，可见在卫星对月定标期间，三台星敏感器的指向与太阳和地气光夹角(α)均大于30°，有效避免了杂光进入星敏感器，满足至少两台星敏感器可用的约束条件，保证了对月观测过程中的姿态控制精度。

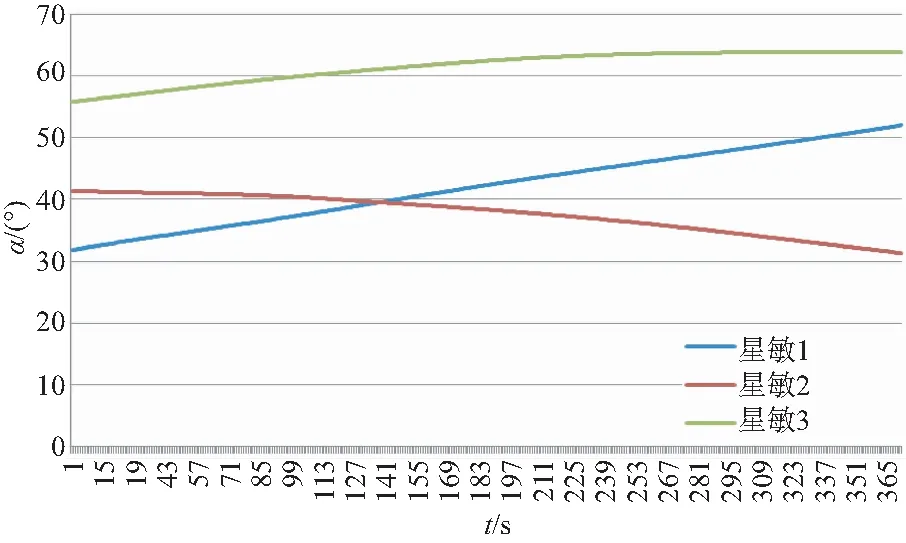
图7 对月定标过程中星敏可用情况Fig.7 Available star sensor in calibration process

以7月15日对月定标实验为例，分析本文提出的卫星姿态规划执行情况。载荷视轴矢量与月球矢量的夹角(β)遥测数据如图8所示，可见由0 s(惯性姿态1)开始，随着卫星绕本体系俯仰轴对月姿态机动，载荷视轴矢量与月球矢量的夹角逐渐减小，到120 s(惯性姿态2)时，载荷视轴矢量与月球矢量的夹角变为0°，此时载荷视轴指向月心，随后载荷视轴矢量与月球矢量的夹角逐渐增大，载荷视轴矢量逐渐远离月球矢量。由此可知，对月定标实验的卫星姿态实际执行情况与本文设计的卫星姿态规划流程一致。

图8 对月定标卫星姿态规划执行情况Fig.8 Planning implementation of satellite attitude

以7月20日对月定标实验为例，分析本文提出的对月定标方法的效能情况。在南极附近的对月定标STK仿真如图9所示(彩图见期刊电子版)，图中最外侧的1 500 s(绿色)为完整的对月定标模式时间范围，中间的240 s(黄色)为卫星绕本体系俯仰轴对月姿态机动时间范围，内侧的120 s(红色)为载荷开机对月成像时间范围。可见，本文提出的对月定标方法不会影响低轨遥感卫星正常的对地观测任务，当卫星退出对月定标模式后，可继续在下一圈阳照区执行对地观测任务，具有很高的观测效率。

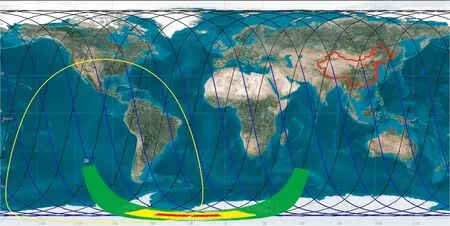
图9 对月观测效能仿真Fig.9 Efficiency simulation of lunar observation

3.3 对月定标图像

卫星下传的原始图像数据经过地面系统处理后，可重建为月球圆盘图像。图10即为本次对月定标实验所获取的多月相角月球图像(全色谱段)，共15幅，月相角覆盖-79.872～89.236°。由于本次实验采用的载荷对地成像的空间分辨力优于2 m，因此对月球观测的空间分辨力要优于1.18 km，这对于我国风云二号、风云三号等静止轨道和极轨气象卫星来说，具有更优的指标特性。由图10可见，获取的月球图像纹理清晰，载荷成像稳定，此外卫星姿态及各分系统遥测均正常。此次实验获取了清晰的月球图像，进一步验证了本文提出的对月定标方法的正确性及合理性，并且实现了中国首次低轨高分辨率遥感卫星姿态机动对月球多月相角观测。

图10 对月定标图像Fig.10 Lunar calibration images

4 对月定标数据应用

4.1 月球圆盘图像重建

本文开展的对月定标实验采用10倍过采样方案，因此卫星下传的原始图像沿推扫方向被拉长，需要经地面系统的去辅助数据处理、镜像处理(与光学系统设计有关)、重采样处理等步骤，恢复重建为月球圆盘图像。图11为全色图像的重建过程，多光谱图像的重建过程同理，不再赘述。

图12为恢复重建后的月球圆盘图像(对应图10中月相角为-7.280°的月球图像)DN值三维显示，可见由于图像左侧的月海面积较大，因此该区域DN值偏低，与实际情况相符。此外，图像整体DN值分布在2 000左右，最大值为3 859，这对于12 bit输出的探测器而言，图像DN值分布层次感较好，也证明了本次对月定标实验采用的载荷成像参数合理。

图11 月球圆盘图像(全色)重建Fig.11 Reconstruction of panchromatic lunar images

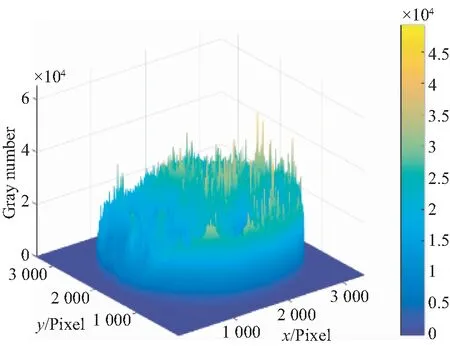
图12 月球圆盘图像的DN值Fig.12 DN value of lunar images

4.2 月球光谱辐照度计算

将月球图像的DN值转化为月球等效反射率是利用月球实现定标的关键[18]。具体计算过程如下：首先，将月球圆盘数据去除暗背景，结合射前实验室辐射定标系数，可将月球图像的DN值转换为月球积分辐射亮度Lp；然后，将月球积分辐射亮度Lp乘以一个像元的立体角δp，得到实验观测月球辐照度I′；接着，将得到的I′转换到标准距离处，得到归一化的平均月地距离384 400 km和1个标准天文单位的月球辐照度I，如式(16)和式(17)所示；最后，利用太阳辐照度光谱将获取的月球光谱辐照度I转换为月球等效反射率A，如式(18)所示。

(16)

fd=(Ds-m/1AU)2(Dv-m/384 400)2，

(17)

A=I·π/(δm·E0)，

(18)

其中：Lp为单个像元DN值减去暗背景平均DN值后转换得到的辐射亮度值，δp为一个像元的立体角，Np为月球圆盘的总像元数，fd为标准距离校正系数，包括校正太阳到月球Ds-m和观测点到月球Dv-m的距离，δm为月球立体角，E0为谱段内太阳光谱辐射强度，A为月球等效反射率。

在得到月球辐照度和月球等效反射率的基础上，可进一步开展月球定标工作，月球定标分为相对定标和绝对定标。相对定标是在“太阳、月球、卫星”三者间几何位置关系固定时，观测到的月球辐照度也保持不变，从而可从长期的对月球观测序列中监测载荷探测器响应率的变化趋势和成像稳定性；绝对定标是在积累大量对月定标数据的基础上，拟合出月球等效反射率与成像几何参数的关系，进而得到月球辐射模型，为月球定标提供辐射基准。

月球辐射模型是度量月球辐射的基准模型，为了校准在轨卫星探测器辐射定标，美国地质调查局(USGS)在美国航空航天局(NASA)的EOS项目资助下，开展了ROLO地基月球观测计划。经过8年的地基对月观测，在350～2 450 nm的32个波段上获取了月相角±90°内的8万余幅月球图像，得到了各种观测条件下月球辐照度的周期性变化规律，最终形成了ROLO月球辐射模型，其绝对不确定度为5%～10%，相对不确定度为1%～2%，目前已应用于遥感探测器的辐射定标和辐射响应衰减监测，我国也正在发展自主知识产权的月球辐射模型[19-21]。

通过本文对月定标实验，计算得出的全色谱段月球辐照度与月相角的关系如图13所示。可见在月亏和月盈时，月球辐照度呈不对称分布，即在月相角绝对值相等的情况下，月亏(正月相)的辐照度小于月盈，这与月亏时月海面积大于高地面积的事实情况相符。同时，图13中月球辐照度分布趋势与国际上ROLO模型公布的月球辐照度曲线趋势一致[5]，产生定量化差异的主要原因包括卫星定标参数偏离发射前实验室定标结果以及对月观测样本数量不足。因此，本文的研究成果可为大量积累对月定标数据、建立中国自主可控的月球辐射模型提供支撑。

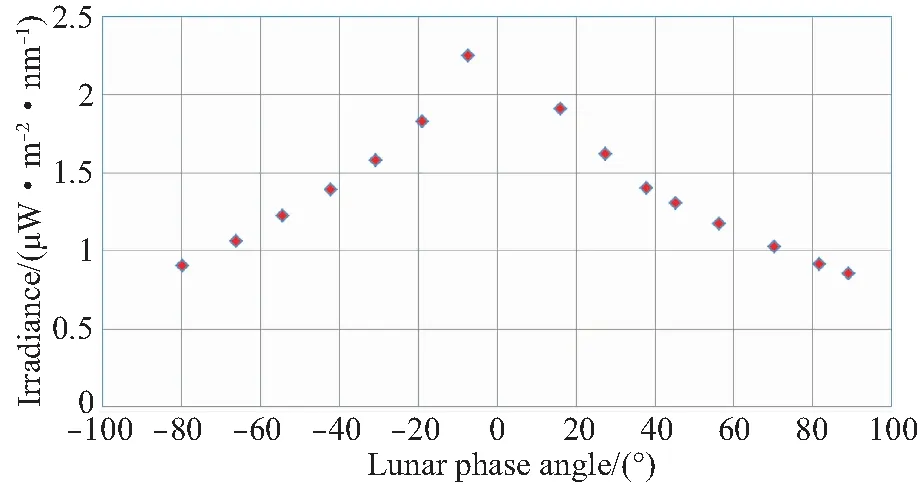
图13 对月定标实验全色谱段月球辐照度与月相角的关系Fig.13 Relationship between lunar irradiance and panchromatic lunar phase angle

5 结 论

本文针对低轨高分辨率遥感卫星提出一种在轨姿态机动对月定标方法，分别从对月定标时机、对月定标卫星姿态以及载荷成像参数等方面详细分析了在轨对月定标的关键技术。该方法不需要对卫星进行轨道控制，与传统的业务模式没有本质区别，不会影响卫星的寿命。同时，也是对传统地面定标场定标的一种补充手段，利用天然的月球定标源，可以大大提升遥感卫星的在轨定标效率。2019年7月依据本文提出的对月定标方法，基于某在轨运行的低轨光学遥感卫星，成功开展了15次对月定标实验，月相角覆盖-79.872°～89.236°。实验结果表明，卫星姿态实际执行情况符合本文设计的对月定标卫星姿态规划流程，并且该对月定标方法具有很高的观测效率，不会影响卫星正常的对地观测任务；地面获取重建的15幅月球图像纹理清晰、稳定，对月球空间分辨力优于1.18 km，图像DN值分布层次感较好；计算得出的月球辐照度分布趋势与国际上ROLO模型公布的月球辐照度曲线趋势一致。实验结果验证了提出的对月定标方法的正确性及合理性。同时，实现了中国首次低轨高分辨率遥感卫星姿态机动对月球多月相角观测，可为长期监测遥感卫星探测器成像稳定性和大量积累对月定标数据、建立中国自主可控的月球辐射模型提供支撑。