微孔式数字PCR荧光芯片的自动对焦

朱文艳，周连群，张芷齐，李金泽，李龙辉，4，高 旭，李树力，5，郭 振*，姚 佳，3*

(1.中国科学技术大学，安徽 合肥 230026；2.中国科学院 苏州生物医学工程技术研究所，中国科学院生物医学检验技术重点实验室，江苏 苏州 215163；3.苏州大学 电子信息学院，江苏 苏州 215006；4.长春理工大学 机电工程学院，吉林 长春 130022；5.上海大学 通信与信息工程学院，上海 200444)

1 引 言

数字聚合酶链反应(Digital Polymerase Chain Reaction，dPCR)是一种测量靶DNA绝对拷贝数的独特方法，是一种绝对定量技术，最早由Saiki等发表[1-2]，与实时荧光定量PCR(Real-time Quantitative PCR，RT-qPCR)相比，dPCR已被证明具有更高的灵敏度，精度及重复性[3-5]。从扩增后的dPCR芯片中获取到有用的信息依赖于dPCR检测分析系统，如进行无创产前检测[6]，人类乳腺癌中HER2癌基因的检测[7]等。目前，dPCR荧光信息的检测方式主要包括两种：一是荧光成像，二是流式细胞荧光分选[8-9]。荧光成像技术随着相机成像技术的发展，其成像速度越来越快，分辨率也越来越高，这种成像方式在显微成像中得到越来越广泛地应用[10-12]。

荧光成像技术易存在失焦的问题，针对微孔式数字PCR信息统计对于高质量荧光图像的需求，若图像离焦问题严重，则会影响统计数据的准确性。不同样本之间垂直位置的差异性，导致相机获得的图像呈现不同程度的模糊，因此，对焦在光学视觉成像系统中起着重要作用，例如各类相机、扫描仪、显微镜[13-14]。而自动对焦可以在最少的人工干预下获得清晰图像[15-16]，进而获得准确的统计数据。为快速获取清晰的图像以便于后续数据处理得到准确的检测结果，必须根据样品变化动态的改变样品与物镜或物镜与成像面之间的距离，以实现样品的自动对焦[17]。

自动对焦可以通过主动、被动或者两者混合来实现[17-19]。主动方法一般是通过激光等测距工具来测量离焦距离后进行对焦，需要在系统中额外嵌入测距系统，并且当使用激光时，会造成芯片上的荧光基团淬灭[20]，对后续数据的准确性造成影响。被动方法可以分为相位检测法和对比度检测法，前者通过测量两幅图像之间的相位差来估计聚焦位置，依赖于特殊的传感器检测系统[21]；后者计算每一帧的清晰度以寻找最佳位置，无需额外检测附件，精简整体系统，降低成本[22-23]，但搜索每一帧并计算，明显增加了计算量和搜索步骤，进而造成对焦时间延长。

考虑到微孔式数字PCR芯片弱荧光样本分布差异造成其计算对象存在片内差异与片间差异，若对焦方法不当，荧光基团长时间暴露在激发光下会发生淬灭，影响后续结果统计。为了实现快速且准确对焦，本文基于数字PCR芯片多个排列孔的特征，提出了一种新的对焦算法，单曲线拟合函数法。通过计算包含单个孔的区域内大于阈值的像素的个数，得到随离焦距离变化，其像素数变化的曲线。在这里，阈值随图像平均灰度的变化而变化，从而得到一条与图像灰度无关的像素数随离焦距离变化曲线，通过正弦函数拟合得到该曲线的拟合函数，即为微孔式数字PCR芯片的对焦评价算法。通过该对焦算法，可以快速得到离焦图像的离焦距离与离焦方向，进而实现快速准确对焦。

2 实验原理

2.1 光学成像系统

自动调焦的目的是通过对光学成像系统的不断校正，使其能够对目标清晰成像，为后续的图像处理、信息提取提供纹理丰富、画面清晰的图像。对于不同结构的任何光学成像系统，其成像原理基本一致，如图1所示(彩图见期刊电子版)。OP和IP分别表示物平面和像平面，D为透镜直径，R为模糊圆半径，u为物距，v为图像距离，s为透镜到图像检测器平面上的距离。黄实线和蓝虚线表示成像对象不同物距的聚焦结果。

根据几何光学原理，物距u、像距v与焦距f满足高斯成像公式，如式(1)：

(1)

由高斯成像公式可知，对于固定焦距的成像系统，物空间任意物距的目标点在像空间存在唯一确定的点与其对应。当目标离焦时，目标点在图像探测器上的像不再是清晰的点，而是一个半径为R的弥散圆。结合光学系统的成像模型，根据三角形相似原理可以得到光学系统参数与弥散圆半径的关系式满足式(2)[24]：

(2)

根据式(1)和式(2)可得弥散圆半径R的具体值为式(3)：

(3)

根据式(3)，当s=v时，弥散斑半径R=0，物点OP在图像探测器上的像为理想的像点；当s≠v时，则有R≠0，物点OP在图像探测器上的像便不再是一个理想的点，而是一个半径为R的弥散斑，即产生离焦图像。

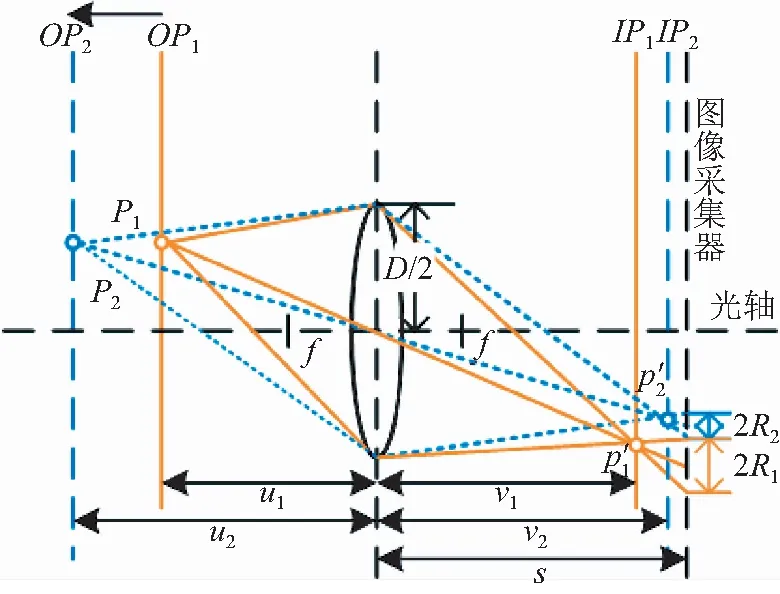
图1 透镜光学成像模型。Fig.1 Lens optical imaging model

弥散斑亮度分布可以通过简单的圆盘模型来近似[25]，如式(4)所示：

(4)

其中R是弥散斑半径。

传统的成像理论认为，固定对象成像的综合强度应与聚焦无关[26-27]。因此，图像离焦是一个弥散斑半径逐渐变大，亮度分散的过程，拥有高亮度的像素数也逐渐减少，表现为亮度分布逐渐呈现均匀性，若灰度阈值选取得当，离焦过程中，大于该阈值的像素数逐渐增大，而在准焦时取得最小 值。

(a)微孔阵列芯片(a)Microarray chip

(b)芯片部分放大图(b)Enlarged image图2 数字PCR系统的成像对象Fig.2 Imaging objects of the digital PCR system

在本文中，系统的成像对象是完成进样及封装的微孔阵列芯片，芯片上规则排列的微孔，将稀释的dPCR样本溶液分割，一部分微孔内填充有DNA样本，引物及特异性的荧光探针，DNA每扩增一条DNA链，就会产生一个荧光分子。经过热循环的芯片在激光激发的作用下，荧光分子累积的孔呈现高亮度，其他孔亮度则无较大区别。如图2所示，芯片内灰度差异的存在及芯片间灰度差异的存在，使得传统的根据像素灰度梯度差来评价离焦量的自动对焦体系出现了片内差异及片间差异，这就要求其计算窗口需要尽可能大以减少这种误差，从而增加了计算量。

采用包含单孔的一定区域内，大于某一阈值像素数量的变化曲线对焦评价算法，其计算对象为单孔及其附近区域，在保证对焦精度的条件下，可以选择很小的对焦窗口，只需包含单孔及其附近区域，从而减小计算量。因此，该对焦算法理论上可以实现微孔式数字PCR芯片的准确快速对焦。

3 大于阈值的像素数量的调焦算法

3.1 自适应对焦窗口的选取

对焦窗口是在自动对焦过程中利用评价函数对拍摄场景进行清晰度评价所选取的某一区域，通常为人们所感兴趣的区域(Region-of-interest，ROI)，而非对整幅图像进行计算。对焦窗口的选择影响对焦精度和速度[18]。窗口太大则包含过多背景对象，导致数据冗余，从而增加计算负载；窗口选择太小，可能丢失关注对象的部分数据，因而合适的对焦窗口对完成快速对焦很重要。

常用的窗口选择算法有，中央区域对焦窗口选择法[28]、多区域对焦窗口选择法、非均匀采样对焦窗口选择法等[29]。这些方法在一定程度上节省了计算时间，在一些领域具有实用价值，但这些方法一旦选定区域后，对焦窗口就固定不变，面对不同的对焦对象及对焦过程中出现的物体偏移情况无法做出有效应对，所以需要根据对焦对象及离焦距离的不同自适应选取对焦窗口以提高对焦精度。

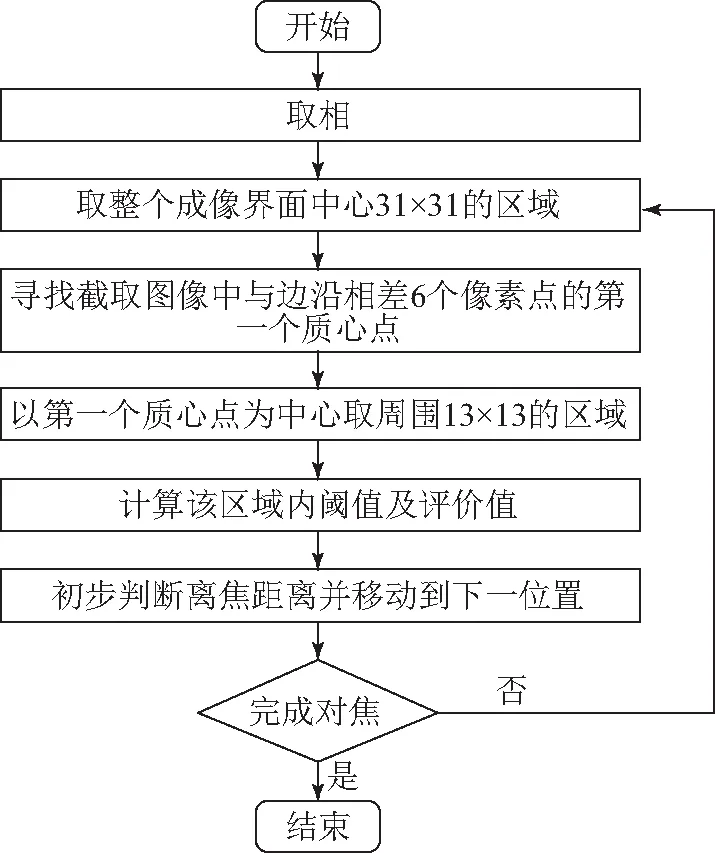
图3 自适应窗口选择流程图Fig.3 Adaptive window selects flowchart

基于大于灰度阈值像素数量的自动调焦算法选取对焦对象的步骤为：首先选取视野中心31×31 pixel区域，在该区域中寻找与截取图像边沿相差6 pixel的第一个质心点；以第一个质心点为中心取周围13×13 pixel的区域为对焦窗口；然后所计算该区域的阈值及评价值，获得离焦数据并进行对焦后将会判断是否完成对焦。若是，则结束，若否，则在下一次对焦前再进行一次窗口选取步骤，进而做到自适应窗口选取。根据不同对焦对象自适应选取对焦孔的步骤如图3所示。

3.2 基于最值的自动阈值选取

判断阈值的选取关系到对焦准确度，同时又要随样本的改变而自动变化，才能达到自动准确对焦的目的。文中根据对焦对象的特征提出了基于区域最值的自动阈值选取方法，在跟随样本变化的同时，能够做到准确对焦。

在对焦区域内，根据区域内的最大值与最小值变化曲线可知，其最值的和在一定范围内呈现一个稳定的值，这个稳定的值除以一个经统计后得出的固定的系数，即为所取阈值如式(5)：

T={max(Iout(x，y，zr))+min(Iout(x，y，zr))}/2.5，

(5)

其中：T表示所取阈值，Iout表示样本I在zr处的离焦图像。

阈值T随对焦对象的亮度增大或减小，提供了一个具有普适性的阈值选取办法，同时为下面的评价算法的提出奠定了基础。如图4所示，x轴表示图像位置的变化，y轴表示灰度最值的变化。红色表示maxI，黄色表示minI，蓝色表示(maxI+minI)/2.5(彩图见期刊电子版)。

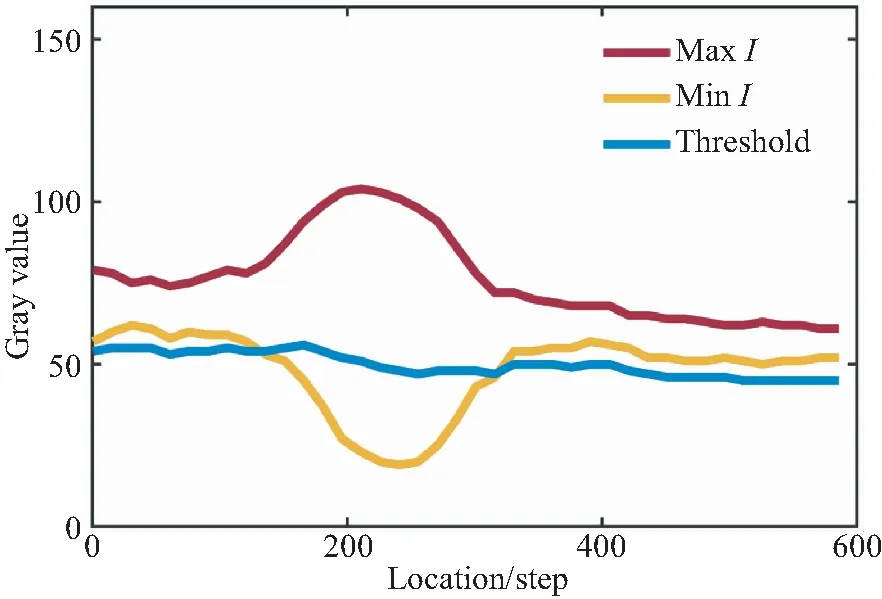
图4 灰度最值曲线及阈值曲线Fig.4 Gray minimum and maxmum curve and threshold curve

3.3 大于自动阈值的像素数量变化评价算法

依据对焦窗口的选取及阈值的选取，通过统计对焦窗口内大于阈值像素点数量的变化，得到对焦评价曲线。

在离焦到正焦再到离焦的序列图像中，图像的离焦量越小，弥散斑半径越小，亮度越集中，大于某一阈值的像素数量值达到最小，如图5所示。x轴表示样本的位置，y轴表示像素数的变化。

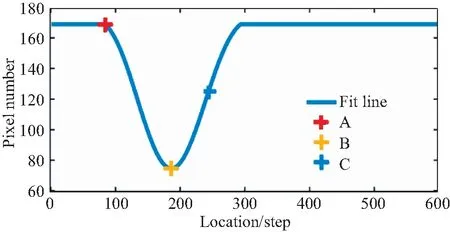
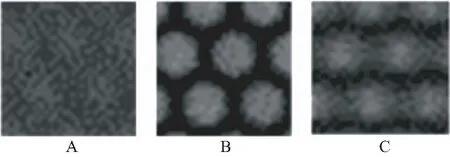
图5 窗口内大于阈值的像素数随位置变化曲线及A，B，C，3点位置对应的微观孔的图像

传统的搜索方法通常根据一些自定义的规则来寻找最高峰，本文通过对不同芯片对焦窗口中不同灰度级像素的数量进行统计得到三组统计数据。如图6所示，组图左侧给出了对焦窗口内像素灰度最大值，最小值以及阈值的变化曲线，根据阈值的取值得到对焦窗口内大于阈值的像素数量的变化散点图，根据散点图的变化趋势拟合出了变化曲线。

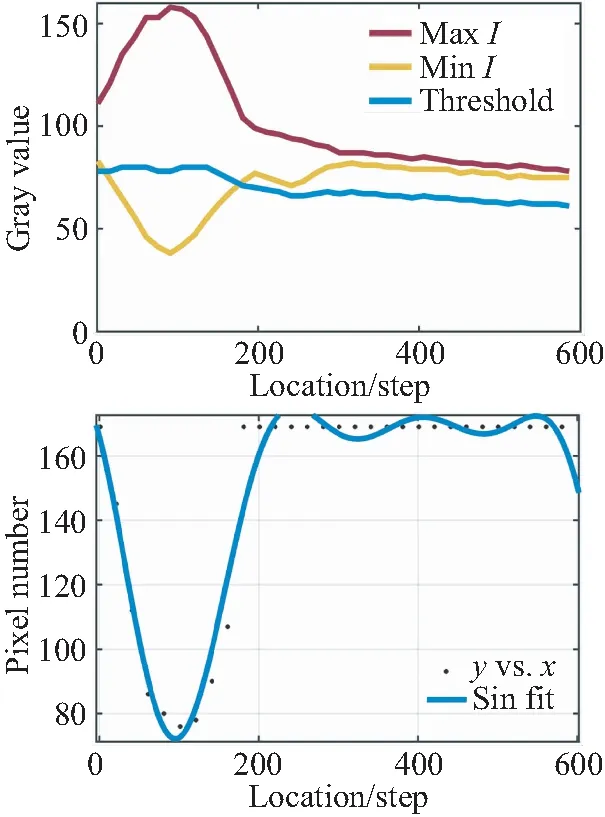
(a)第一组(a)First group

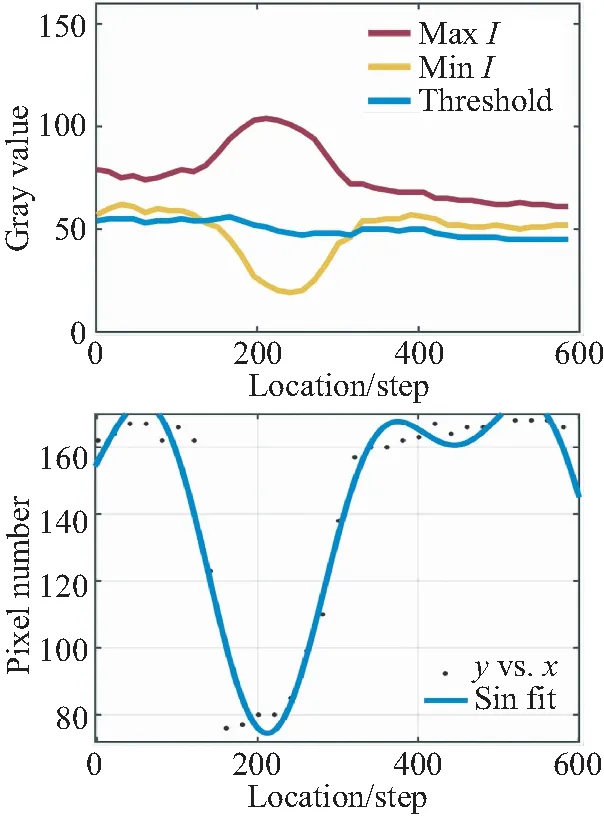
(b)第二组(b)Second group

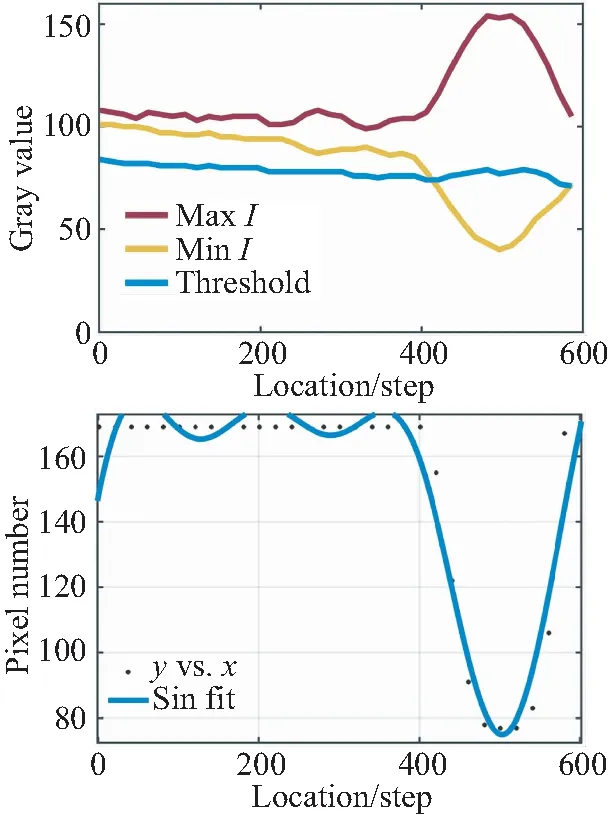
(c)第三组(c)Third group

从3组灰度变化曲线可知，3个样本芯片的灰度最值及阈值选取的大小并不相同。但从像素数量变化散点图及其正弦拟合曲线的变化趋势来说，在此阈值的选取方法下，3组像素数量变化曲线在突变区间横坐标与纵坐标的差值大小，平稳区间的纵坐标的大小上具有一定的一致性。

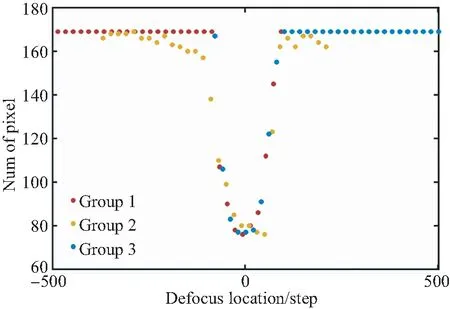
(a)散点图

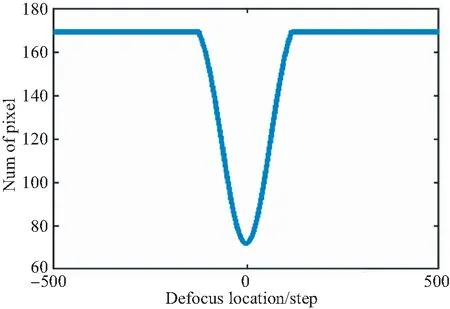
(b)拟合曲线

根据分组图中，大于阈值的像素数量变化趋势的一致性，在同一图中做出像素数量随离焦距离的变化散点图及其拟合曲线[30]，如图7所示。

3组数据中，像素数量随离焦距离的变化趋势主要表现为2个特征：一是在一定离焦距离范围内，对于不同灰度的样本芯片，其像素数随离焦距离的变化趋势呈现高度的一致性，拟合曲线符合四参数正弦拟合曲线的变化特征[31-32]；二是，在上述离焦距离范围之外，对于不同灰度的样本芯片，其像素数量稳定在169，即对焦窗口所包含的总的像素数。这两个特征符合光学成像原理所述的弥散斑半径及亮度分布特征，可用分段函数表示为：

(6)

其中：d表示离焦距离，参数a，b，c表示拟合曲线的参数。在95%的置信区间内，方差R-square为0.944条件下，a，b，c的取值如表1。

曲线的d，f取值只与离焦距离，大于阈值的像素数有关，在窗口和阈值确定的条件下，可认为曲线的变化特征唯一确定。因此，在计算得出大于阈值的像素数后，可根据拟合曲线来计算离焦距离与方向。根据像素数反推出的数字的绝对值代表离焦距离，正负代表方向，为正时，代表取相位置在准焦点位置的下方，应向上运动；为负时，代表取相位置在准焦点位置的上方，应向下运动。

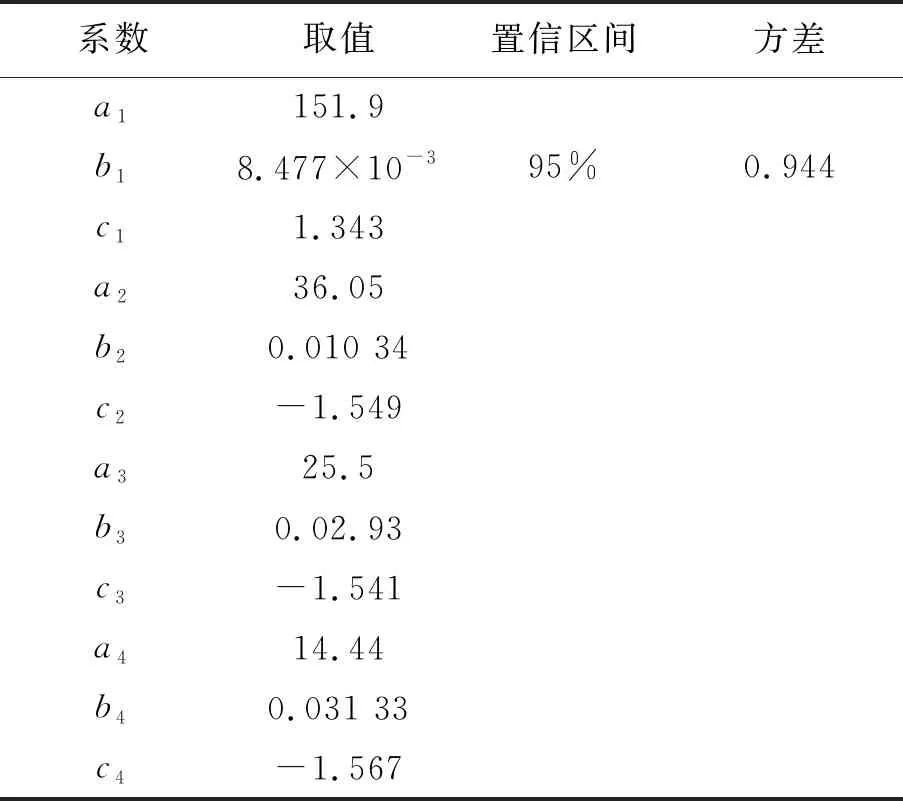
表1 拟合曲线系数

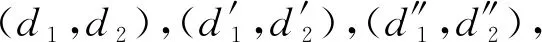
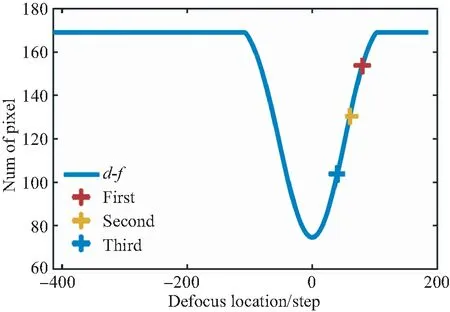
(a)f1(d)>f2(d)>f3(d)

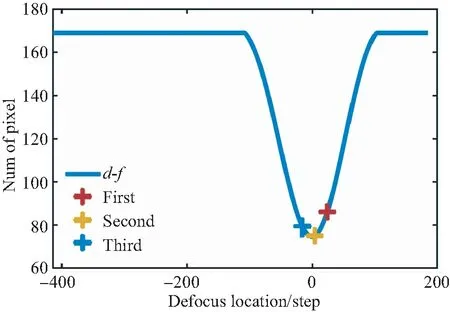
(b)f1(d)>f3(d)>f2(d)

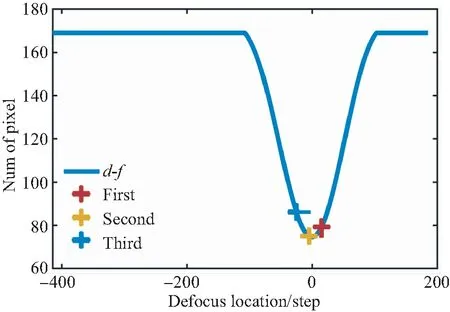
(c)f3(d)>f2(d)>f1(d)

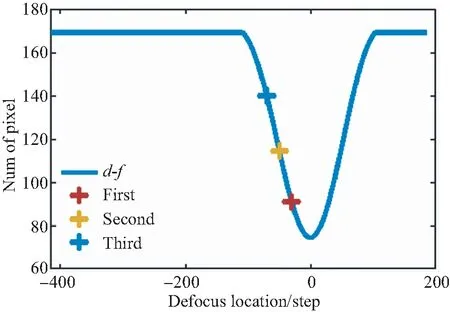
(d)f1(d)>f3(d)>f2(d)图8 根据3个位置像素数值分布情况进行方向判断Fig.8 Judging the direction according to the distribution of the number of pixels in 3 locations

4 结果与分析

为了评估所提出方法的有效性和效率，本文对3张新的芯片进行测试，每张芯片采集A，B，C共3组不同初始位置的数据，每组数据包含3个等间隔位置的图像。通过计算每个位置图像上大于阈值的像素个数，来计算离焦距离和进行离焦方向的判断，结果如表2～表4，图9～图11。此外，每张芯片在离焦到正焦再到离焦的过程中都均匀的提取了600张图像，对每组的600张图片进行处理，并利用清晰度计算方法对每组图像进行计算统计，做出清晰度评价值拟合曲线，选取曲线的最值对应的位置作为准焦点位置，进而计算出每个初始位置的实际离焦距离。

表2、表3、表4中分别统计了每张芯片的灰度及每个位置的计算离焦信息，并与实际离焦信息进行对比，得出对焦误差，该误差反映到实际图像上，即为图9、图10、图11。

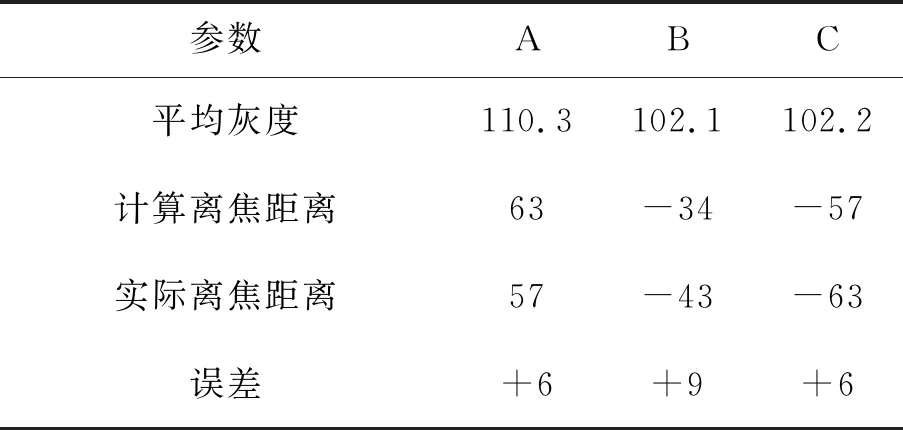
表2 第一张芯片测试数据

图中Initial列是芯片位于初始位置时整幅芯片图像及5个区域微观图，A，B，C组分别代表3个初始图像；Autofocus列是对焦后整幅芯片图像及5个区域微观图，A，B，C组分别代表3幅对焦后图像；Focus right，即D组是准焦点整幅芯片图像及5个区域的微观图，图中的红色方框代表截取的图像在整幅芯片图像中所处位置。

Autofocus列的A，B，C三组图像中，孔与孔之间已经可以明显分辨。经过与准焦点的D组图像对比发现，在肉眼观察条件下，并不能清晰判别几幅图像之间的差异。在预设清晰度条件下，所有对焦测试结果已满足后续计算要求，经过测试，目前所界定的清晰地范围为准焦点上下15个位置。

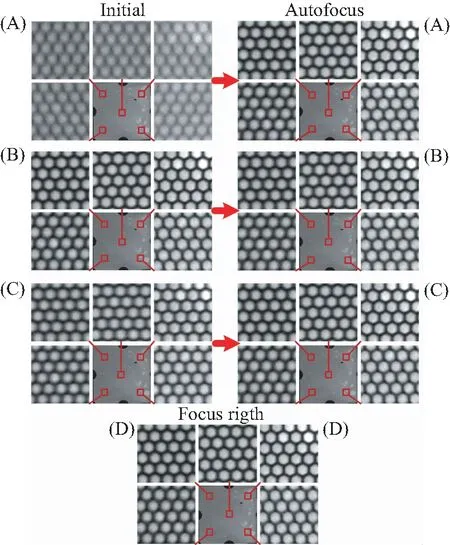
图9 第一张芯片准焦图像与3组对焦前后图像Fig.9 First chip quasi-focal image and three groups of pre-and post-focal images

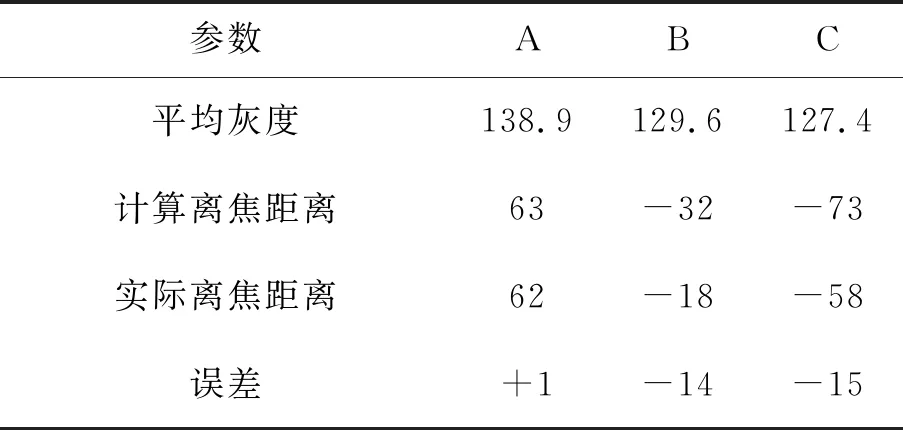
表3 第二张芯片测试数据

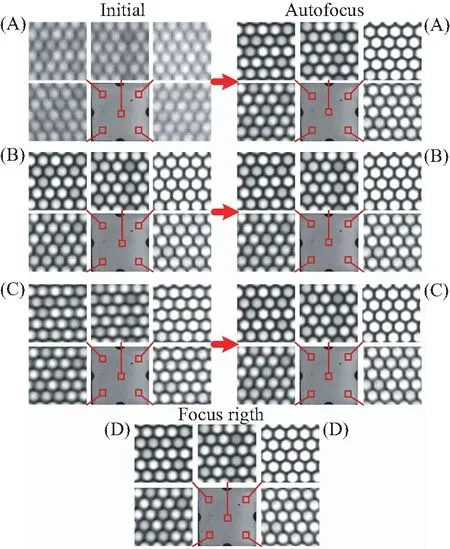
图10 第二张芯片准焦图像与3组对焦前后图像Fig.10 Second chip quasi-focal image and three groups of pre-and post-focal images

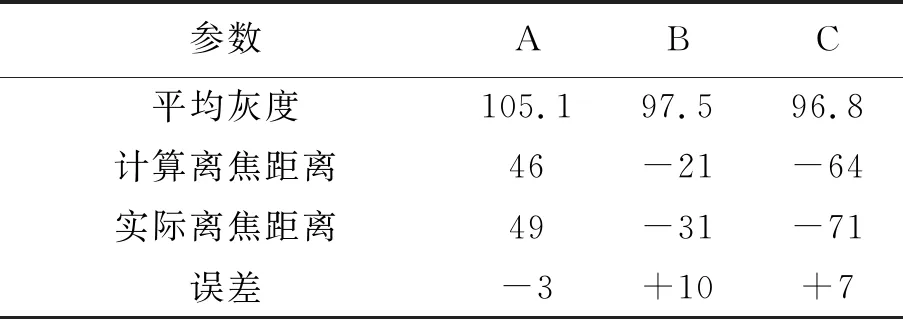
表4 第三张芯片测试数据

图11 第三张芯片准焦图像与3组对焦前后图像Fig.11 Third chip quasi-focal image and three groups of pre-and post-focal images

以速度和准确性为标准，在同等初始条件下，与传统的爬山算法进行比较(各类爬山算法的区别主要在于步长与精度的选择上，但是基本思想是相同的)。Hen等[33]提出粗细结合的对焦方法，该方法采用粗略或较大步距找到一个峰值，然后反转方向采用精细或较小步距来缩小范围。峰和反转方向、停止搜索的条件是手动创建的，不同研究者给与的峰和反向以及停止搜索的条件是不同的。在这里，根据对象创建的搜索条件是，粗搜索步距，20个位置差，较为精细搜索，10个位置差，初始搜索方向定位向上搜索，搜索到峰值即停止搜索，对焦过程中，每运动一步均需要重新取相计算，直到完成对焦。假设使用两种不同的算法在相同的初始位置对同一样本进行对焦，并且电机驱动位移台进行相同的匀速运动，以此忽略多次启停造成的时间延长，则在对焦过程中耗费时间的动作集中在取相计算上，当对焦所需步骤数越多，重复取相与计算次数越多，整体上对焦耗时越多。若不忽略多次启停造成的时间延长，则步骤数越多，启停引起的时耗越多。因此，文中以所需步骤数的多少的来评价对焦过程的快慢[34-35]，对传统爬山搜索算法和本文中所提算法对焦过程中所需步骤数进行了统计。文中所提方法完成对焦仅需4步，与传统爬山算法相比，步骤数明显减少，并在表5中做出统计。

同时，爬山完成所需步骤数明显与芯片的初始位置以及初始运动方向的设定有关。当设定初始方向为向上，芯片初始位置位于焦点以下比初始位置位于焦点以上对焦步骤数明显减少，原因是少了第三次取相后的换向过程。另外，若爬山步距设置较小，并且评价函数选取不恰当，搜索过

程中很容易陷入局部极值，在未到达峰值点的情况下就退出搜索，对焦过程中断。

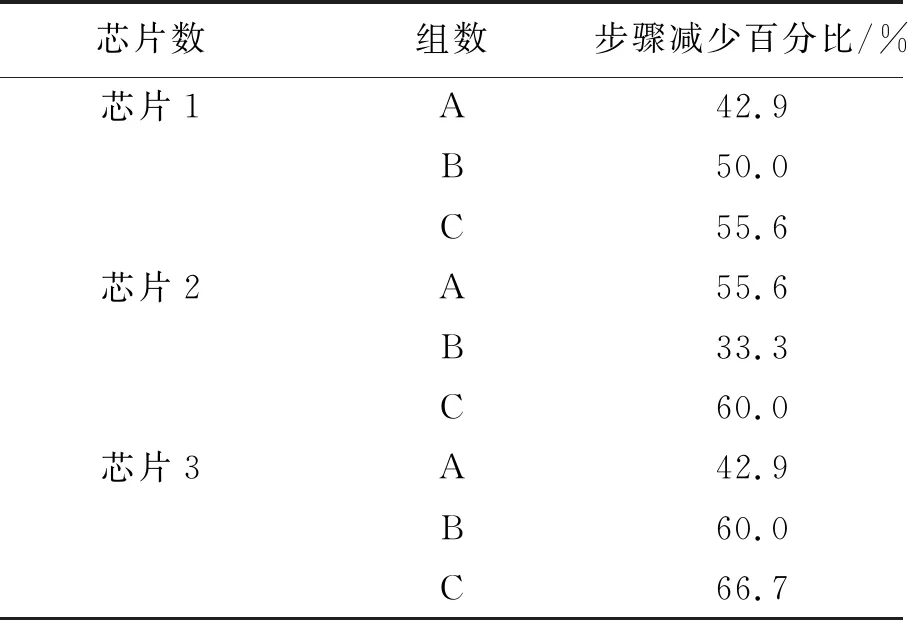
表5 不同对焦方法所需步骤数对比

5 结 论

以上研究表明，一定区域内，通过灰度大于阈值的像素数变化曲线作为微孔式数字PCR芯片的自动对焦算法是可行的。利用对焦窗口和判断阈值的自适应选取，统计窗口内大于阈值的像素数，并得出其随离焦距离变化的特征拟合曲线以及曲线的函数表达式，该函数在后续测试中成功实现了对焦。该方法不受灰度变化的影响，与混合爬山对焦方法相比，对焦步骤数最少减少了33.3%，最多减少了66.7%，平均减少了51.89%，实现了微孔式数字PCR芯片微尺度阵列单元的准确快速对焦，在最大程度上减少荧光曝光时间，进而减少荧光的淬灭，为后续计算提供更为原始而准确的图像。