讨价还价博弈均衡出价策略的算法设计

徐齐利

江西财经大学 经济学院，南昌 330013

1 引言

在智能时代，博弈论与计算机交叉，形成一门新兴学科：算法博弈论[1-3]。博弈论关注的焦点是构建博弈模型和分析博弈均衡[4-5]；算法博弈论关注的焦点则是求解博弈均衡，即如何求解博弈模型的博弈均衡[6-7]。算法博弈论在商业智能领域具有非常广阔的应用需求[8-11]。例如，在智能电子商务的讨价还价博弈中[12-14]，买卖双方的均衡出价策略该如何求解。

买卖双方轮流出价的讨价还价博弈属于典型的动态博弈，即后行动的人能看到先行动的人其行动的博弈，而求解动态博弈的基本思想是逆向归纳法[15]。逆向归纳法仅是求解动态博弈均衡的一般思路，其在计算机上并不具有可实现性。但基于逆向归纳法，可以开发出具体某类动态博弈的具体求解算法。针对讨价还价博弈，如何求解买卖双方的均衡出价策略，本文开发出两个可计算机实现的算法：基于逆向归纳过程，设计出迭代算法；基于逆向归纳结果，设计出递归算法。

从算法的设计思路来看，迭代算法是逆向归纳法的具体实现；而递归算法则并不拘泥于逆向归纳法，是一种全新的博弈求解思路。从算法的实验测试来看，这两个算法不仅高效、实用，还同时得出均衡出价策略的上下包络线。从算法的实际应用来看，算法所得的上下包络线是买卖双方最优出价的控制线，这对电子商务智能出价系统的设计至关重要。因此，本文还将电子商务的讨价还价实战分设司令部、参谋部、作战部等三个角色模块，给出应用该算法开发智能出价决策支持系统的初步设计思路。

2 模型

2.1 博弈案例

某商品，买方的意愿支付为v，即买方最高愿以v的价格购入；卖方的意愿支付为c，即卖方最低愿以c的价格售出；买卖双方经过t=1,2,…轮讨价还价之后，最终以p(t)的价格成交。前提假设：买方的意愿支付v、卖方的意愿支付c、买卖双方最终的成交价格p(t)三者之间的大小关系为v≥p(t)≥c；否则，买卖不可能达成。

买卖双方之所以会讨价还价，表面上看，当然是由于买方想尽量少出钱，卖方想尽量多收钱；实质来看，则是对交易总剩余v-c这个蛋糕的零和博弈。成交后，卖方从中获得剩余p(t)-c，买方从中获得剩余v-p(t)。

既然买卖双方讨价还价博弈实质是关于分蛋糕的博弈，不妨设：经历t=1,2,…轮讨价还价达成交易后，卖方获得蛋糕的份额为x1(t)，卖方获得蛋糕的份额为x2(t)。两份额函数满足关系式：0 ≤x1(t),x2(t)≤1，x1(t)+x2(t)=1。引入份额函数后，卖方的实际支付结构为p(t)=c+x1(t)(v-c)，买方的实际支付结构为p(t)=v-x2(t)(v-c)，这就是说，买卖双方最终成交价格p(t)的结构为：

可见，买卖双方最终的成交价格实际上是买卖双方意愿支付价格的加权平均，权重为各自在总剩余中所获剩余的份额。

2.2 博弈规则

不失一般性，上述买卖双方讨价还价博弈的规则设定为：第1 轮，卖方出价，买方若接收卖方的出价，则双方以卖方以此次出价成交，博弈结束；若买方不接受卖方的出价，则博弈进入第2 轮。第2 轮，买方出价，买卖若接收买方的出价，则双方以买方以此次出价成交，博弈结束；若卖方不接受买方的出价，则博弈进入第3轮。第3轮，卖方出价，买方选择接受与否，依次决定博弈是否结束；第4 轮，买方出价，卖方选择是否接受，若还不能达成交易，则买卖双方如此动态博弈下去，直到一方表示接受对方的出价为止。

由式（1）知，上述讨价还价博弈规则可直接简化关于蛋糕分配份额(x1(t),x2(t))的博弈：若t=1,3,5,…为奇数，则(x1(t),x2(t))为卖方提出的分配方案；若t=2,4,6,…为偶数，则(x1(t),x2(t))为买方提出的分配方案。

贴现因子0 ≤δ1,δ2≤1 分别刻画卖方和买方在讨价还价过程中的耐心程度，耐心程度越大（小）的一方，其贴现因子取值越高（低）。第t=1,2,…轮的分配方案(x1(t),x2(t))，将其贴现到博弈刚开始的第1 轮，则其现值为。

2.3 博弈均衡

若t=1，即讨价还价只可经历1 轮，则该博弈的纳什均衡①买卖双方出价的纳什均衡是指：双方都选择了自己的最优出价策略，任何一方偏离该报价策略必将招致自己损失。，以现值(f(t),g(t))表示即为(f( 1),g( 1) )=(1 ,0 )。即卖方提出自己吃独食的分配方案，买方只有接受卖方吃独食，否则买方将得不到该商品。

若t=2，即讨价还价只可经历2 轮，则该博弈的子博弈精炼纳什均衡②买卖双方出价的子博弈精炼纳什均衡是指：双方的出价策略不仅从中间轮次开始至最终结束的子博弈是纳什均衡，而且从最初轮次到最终结束的全博弈也是纳什均衡。，以现值(f(t),g(t))表示即为(f( 2),g( 2 ))=(1 -δ2,δ2)。这是因为，根据动态博弈求解子博弈精炼纳什均衡的逆向归纳法：在t=2 期，买方提出自己吃独食且卖方只能接受的分配方案(x1( 2),x2( 2) )=( 0,1) ；该分配方案贴现到t=1 期，则买方所获份额为δ2。在t=1 期，卖方提出份额分配方案(x1( 1),x2( 1) )=(1 -δ2,δ2)则买方不会拒绝的同时卖方也能取得自己力所能及的最大份额。在该期，若卖方提出给买方的份额x2( 1) ＜δ2，则买方会拒绝该分配方案，随后轮到买方出价时买方会吃独食。若卖方提出给买方的份额x2( 1) ＞δ2，则买方会接收该分配方案，但该方案对卖方自己却是并没有取得自己力所能及的最大份额。因此，(f( 2),g( 2 ))=(1 -δ2,δ2)是2 轮讨价还价博弈的子博弈精炼纳什均衡。

若t=3，即讨价还价只可经历3 轮，则该博弈的子博弈精炼纳什均衡，以现值(f(t),g(t))表示即为(f( 3),g( 3 ))=(1 -δ2(1 -δ1),δ2(1 -δ1))。应用逆向归纳法，推导过程如下：在t=3 期，卖方提出自己吃独食且买方只能接受的分配方案(x1( 3),x2( 3 ))=( 1,0 )；该分配方案贴现到t=2 期，则卖方所获份额为δ1。在t=2期，买方提出分配方案(x1( 2),x2( 2 ))=(δ1,1-δ1)，则卖方不会拒绝的同时买方也挣到了自己最大的份额；该分配方案贴现到t=1 期，则买方所获份额为δ2(1 -δ1)。在t=1期，卖方提出分配方案(x1( 1),x2( 1) )=(1-δ2(1 -δ1),δ2(1 -δ1))，则买方不会拒绝的同时卖方也能取得自己力所能及的最大份额。故(f( 3),g( 3 ))=(1-δ2(1 -δ1),δ2(1 -δ1))是3轮讨价还价博弈的子博弈精炼纳什均衡。

若t=4，即讨价还价只可经历4 轮，则该博弈的子博弈精炼纳什均衡，以现值(f(t),g(t))表示即为(f( 4),g( 4 ))=(1 -δ2(1 -δ1(1 -δ2)),δ2(1 -δ1(1 -δ2)))。此结果是应用逆向归纳法进行迭代计算而来：在t=4期，买方提出自己吃独食且卖方只能接受的分配方案(x1( 4),x2( 4 ))=( 0,1) ；基于此分配结果逆向迭代，在t=3 期，卖方提出分配方案(x1( 3),x2( 3 ))=(1 -δ2,δ2)，则买方不会拒绝的同时卖方自己也挣到了自己在此时力所能及的最大份额；基于此分配结果再次逆向迭代，在t=2 期，买方提出分配方案(x1( 2),x2( 2 ))=(δ1(1 -δ2),1-δ1(1 -δ2))，则卖方不会拒绝的同时买方也挣到了自己最大的份额；基于此分配结果继续逆向迭代，在t=1 期，卖方提出分配方案(x1( 1),x2( 1) )=(1-δ2(1 -δ1(1 -δ2)),δ2(1 -δ1(1 -δ2)))，则买方不会拒绝的同时卖方自己也能取得自己力所能及的最大份额。

同理，对任意有限轮(0 ＜t＜∝ )的讨价还价模型，由逆向归纳法皆可得其子博弈精炼纳什均衡(f(t),g(t))。结合式（1）知，由均衡的剩余分配策略(f(t),g(t))得，讨价还价博弈中买卖双方的均衡出价策略为：

3 算法

3.1 迭代算法

如何求解讨价还价模型子博弈精炼纳什均衡，即如何得出讨价还价博弈中买卖双方的均衡出价策略。基于上述逆向归纳法的思维过程，设计出迭代算法；基于上述逆向归纳法的求解结果，设计出递归算法。

迭代算法设计如下：

步骤1初值

ift为奇数

x1(t)=1；

x2(t)=0；

ift为偶数

x1(t)=0；

x2(t)=1；

end if

步骤2迭代

fori=t-1:-1:1

ifi为奇数

x2(i)=δ2x2(i+1) ；

x1(i)=1-x2(i)；

ifi为偶数

x1(i)=δ1x1(i+1) ；

x2(i)=1-x1(i)；

end if

end for

步骤3结果

f(t)=x1( 1) ；

g(t)=x2( 1) ；

p(t)=f(t)v+g(t)c

整个迭代过程就是逆向归纳法在讨价还价博弈中的实现过程，4个关键点：第一，迭代前的初值设置，出价者首先提出的报价是一种自己吃独食的分配方案，若谈判次数仅此一轮，则对方只能被动接受此方案；否则，对方会否定于己则一无所得的方案，博弈进入迭代程序。第二，迭代中的进程次序，一是逆向迭代，即t→(t-1) →(t-2) →…→3 →2 →1；二是交替迭代，即卖方→买方→卖方→买方→…或买方→卖方→买方→卖方→…。第三，迭代中的递推关系，轮到卖方出价时，递推关系为买方所得份额的一次贴现；轮到买方出价时，递推关系为卖方所得份额的一次贴现。第四，迭代后的结果输出，一要得出均衡的剩余分配策略(f(t),g(t))，二要得出均衡的出价策略p(t)。

图1 列举了部分轮次讨价还价博弈剩余分配策略的迭代算法求解结果。依据该算法：如果讨价还价只进行1次，即t=1，则卖方竟得全部剩余f( 1) =1，买方没有剩余可得g( 1) =0，此时均衡的市场成交价p( 1) =v；如果讨价还价进行2 次，即t=2，则卖方竟得剩余份额f( 2 )=1-δ2，买方竟得剩余份额g( 2 )=δ2，此时均衡的市场成交价p( 2 )=(1 -δ2)v+δ2c；如果讨价还价进行3次，即t=3，则卖方竟得剩余份额f( 3 )=1-δ2(1 -δ1)，买方竟得剩余份额g( 3) =δ2(1 -δ1)，此时均衡的市场成交价p( 3 )=(1 -δ2(1 -δ1))v+δ2(1 -δ1)c；如果讨价还价进行4 次，即t=4 ，则卖方竟得剩余份额f( 4 )=1-δ2(1 -δ1(1 -δ2))，买方竟得剩余份额g( 4 )=δ2(1-δ1(1 -δ2))，此时均衡的市场成交价p( 4 )=(1-δ2(1-δ1(1 -δ2)))v+δ2(1 -δ1(1 -δ2))c。可见，依迭代算法所得的剩余分配策略(f(t),g(t))与上文枚举法所得结果完全一致。

3.2 递归算法

众所周知，逆向归纳法是求解子博弈精炼纳什均衡的基本思想。上述迭代算法就是逆向归纳法在讨价还价博弈问题上的具体实现，下面提出的递归算法在讨价还价博弈问题上则并不拘泥于逆向归纳法。

第一，均衡分配策略递归算法的递推关系。针对图1 所列部分轮次讨价还价博弈均衡的剩余分配策略(f(t),g(t))，不难发现，买卖双方均衡的分配策略在不同博弈轮次之间的递推关系存在两种模式：自递归模式和交叉递归模式。

自递归模式：当3 ≤t＜∞ ，则：

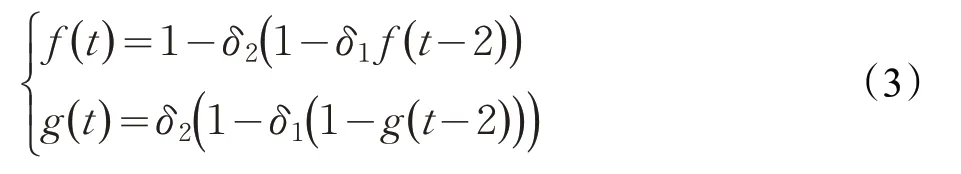
交叉递归模式：当3 ≤t＜∞，则：

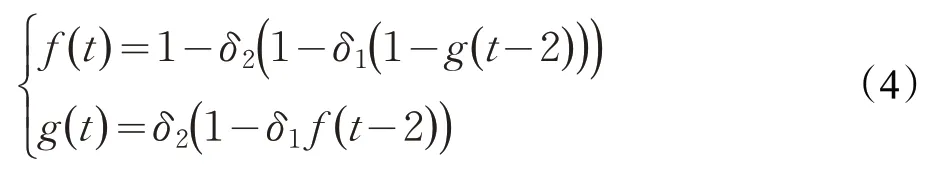
这两种递推关系皆能通过数学归纳法证明其成立。

第二，均衡分配策略递归算法的边界条件。由式（3）、（4）皆为跨两步递推知，均衡分配策略递归算法的边界条件则需2 个，即(f( 1),g( 1) )和(f( 2),g( 2 ))。由图1知，这两个均衡分配策略的具体取值为：

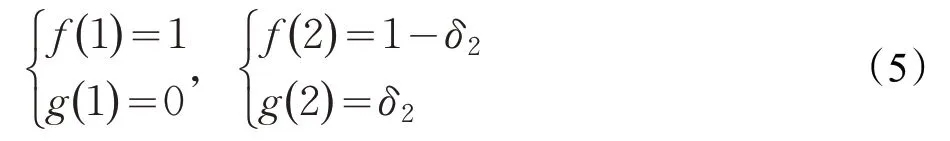
对于如何得出均衡出价策略，自然可与按照迭代算法的思路同理，在递归之后所得均衡出价策略f(t)和g(t)具体取值的基础上，按照式（2）得出均衡出价策略p(t)的具体取值。例如，可以按照如下的结构对卖方均衡的剩余分配进行递归：

以此得到均衡出价策略及买卖双方所得的剩余分配策略。当然，也可以根据式（3）或式（4）均衡出价策略的递推关系，按照式（2）构建均衡出价策略的递推关系，进而形成均衡出价策略的递归算法。均衡出价策略递归算法具体设计如下。

第三，均衡出价策略递归算法的递推关系。将式（3）或式（4）均衡出价策略的递推关系代入式（2）得到，均衡出价策略的递推关系：当3 ≤t＜∞，则：

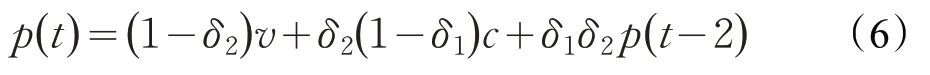
后经数据归纳法证明知均衡出价策略的该递推关系确实成立。

第四，均衡出价策略递归算法的边界条件。将式（5）代入式（2）得均衡出价策略递归算法其边界条件p(1 ),p( 2 )具体取值的计算公式为：

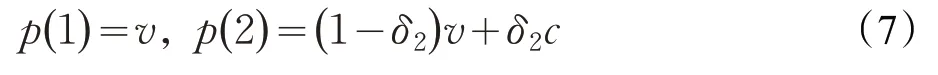
利用式（6）、（7）设计的递归算法，图2 给出部分轮次讨价还价博弈均衡出价策略p(t)的解析表达式。图2与图1按照式（2）完全吻合，说明递归算法和迭代算法所得结果是一致的。在随后的实验测试阶段就要对这种一致性关系进行验证，此对两种算法进行校验。

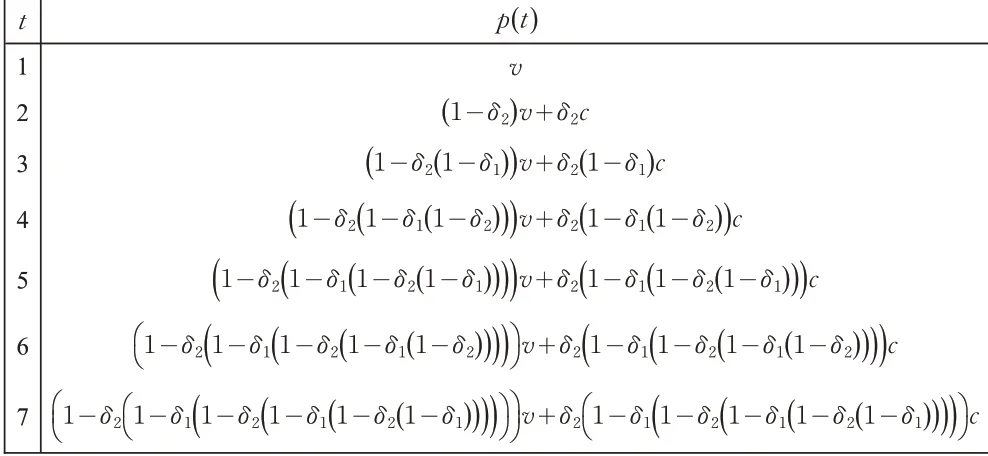
图2 讨价还价模型的子博弈精炼纳什均衡：均衡报价策略

3.3 算法的收敛性

Rubinstein[15]指出，在无限轮讨价还价博弈中，剩余分配策略(f,g)唯一的子博弈精炼纳什均衡结果为应用该结论，如果设计的算法在t→∞时均衡的剩余分配策略(f(t),g(t))不收敛到，则说明所设计的算法是错误的。

为考察均衡分配策略算法的收敛性，根据式（3）或式（4）建立如下方程组：

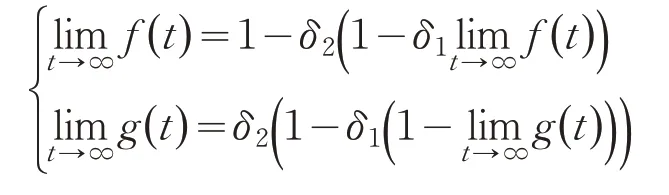
或

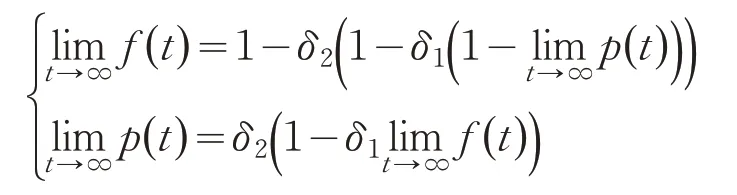
解方程组得：

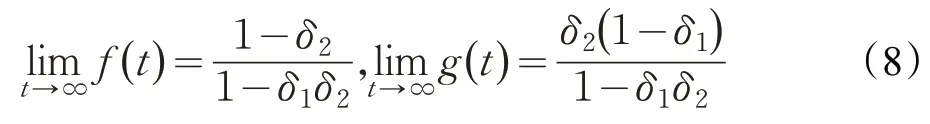
式（9）表明，就收敛性而言，所设计的均衡分配策略算法是合理的。

进而考察均衡出价策略算法的收敛性，根据式（6）建立如下方程：

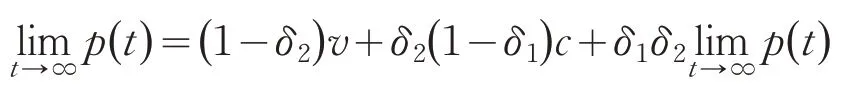
解方程得：

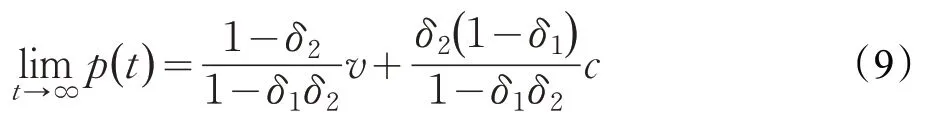
式（9）与式（8）之间满足关系式：

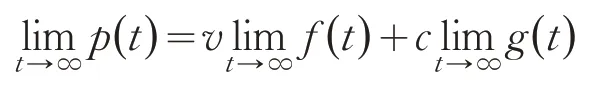
该式与式（2）完全吻合，说明，就收敛性而言，所设计的均衡出价策略算法也是合理的。在接下来的实验测试阶段，算法的实现过程需要充分体现式（8）、（9）的收敛性。

4 实验

4.1 均衡分配策略

为测试上述迭代算法和递归算法的有效性，实验用的参数设置为：买方的意愿支付v=100，卖方的意愿支付c=50，卖方的贴现因子δ1=0.8，买方的贴现因子δ2=0.8。

迭代算法和递归算法所得均衡分配策略(f(t),g(t))随讨价还价轮次t变化的路径皆如图3 所示。图中，实线表示的曲线是卖方所得份额f(t)随讨价还价轮次t变化的路径；穿过该曲线的水平直线是函数f(t)的水平渐近线，该渐近线在纵轴上的取值刚好等于无限轮讨价还价博弈在纳什均衡时卖方所得份额(1 -δ2)(1 -δ1δ2)=0.555 6。虚线表示的曲线是买方所得份额g(t)随讨价还价轮次t变化的路径；穿过该曲线的水平直线是函数g(t)的水平渐近线，该渐近线在纵轴上的取值刚好等于无限轮讨价还价博弈在纳什均衡时买方所得份额δ2(1 -δ1)(1 -δ1δ2)=0.444 4。可见，就均衡分配策略而言，实验测得算法收敛性恰是式（8）理论所示算法收敛性的具体反映。

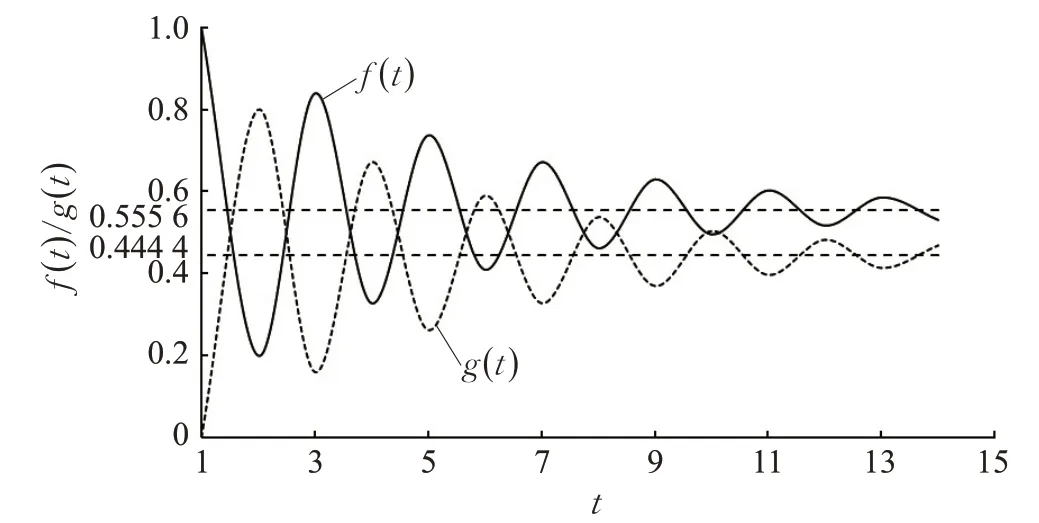
图3 (f ( t ),g( t ))随t 的变化路径

算法出现收敛性仅是对均衡分配策略未来命运的刻画，讨价还价毕竟不能无限轮没完没了地持续下去，经历有限轮讨价还价即可达成交易才是现实常态。图3的测算结果显示：若经历奇数轮讨价还价，则先出价的卖方所得份额多；若经历偶数轮讨价还价，则后出价的买方所得份额多。由此可见，所设计的算法完全体现了有限轮讨价还价博弈的基本理论：奇数轮讨价还价，先发有优势，后发优劣势；偶数轮讨价还价，先发有劣势，后发有优势。这就是说，利用该算法，就可以在电子商务的讨价还价智能谈判中关于双方的盈余分配不仅能做到“知己知彼”，还能做到“趋利避害”。

4.2 均衡出价策略

迭代算法和递归算法所得均衡出价策略p(t)随讨价还价轮次t变化的路径皆如图4的实线所示。图中，曲线p(t)上包络线为奇数轮讨价还价所形成的均衡价格，该价格对卖方有利；曲线p(t)下包络线为偶数轮讨价还价所形成的均衡价格，该价格对买方有利；穿过该曲线p(t)的水平直线是函数p(t)及其上下包络线的水平渐近线，该渐近线在纵轴上的取值刚好等于无限轮讨价还价所形成的均衡价格[( 1 -δ2)v+δ2(1 -δ1)c](1 -δ1δ2)=78.777 8。可见，就均衡出价策略而言，实验测得算法收敛性恰是式（9）理论所示算法收敛性的具体反映。

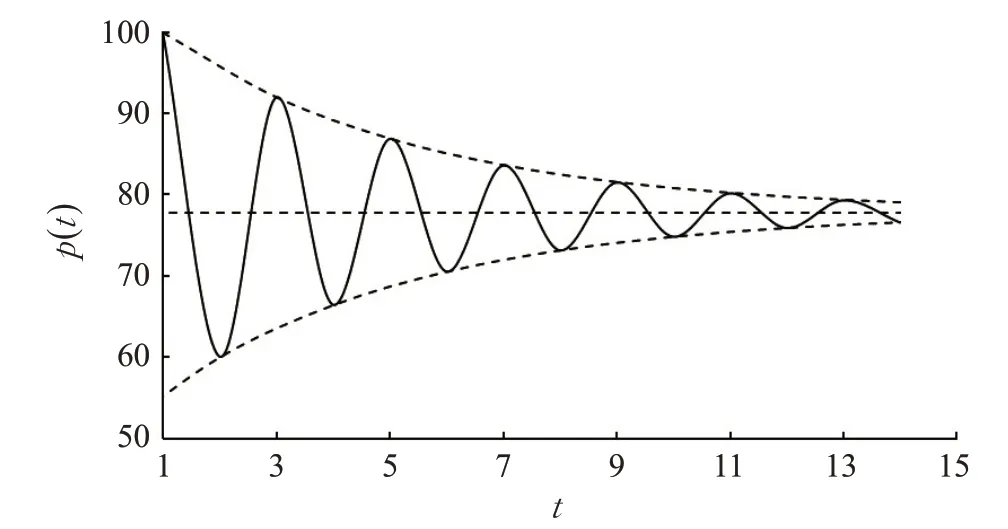
图4 p( t )随t 的变化路径

图3、图4共同反映，即便买卖双方耐心程度和谈判能力完全一样，只要讨价还价的轮次足够长，均衡的成交价格总是高于公平价格（本例的公平价格(v-c)2=75.00），此时，卖方总是处于获得较多盈余的有利地位，买方总是处于获得较少盈余的不利地位。这恰是算法的收敛性式（8）、（9）在贴现因子δ1=δ2=δ时所能揭示的。

5 应用

在电子商务的讨价还价实战中，应用该算法的商业智能决策支持系统该如何开发，下面分商业实战的司令部、参谋部、作战部等三个角色模块，给出初步的设计思路。

对商业实战的司令部而言，可按照该算法的上下包络来部署战略决策：（1）在奇数轮讨价还价中，先出价的卖方当选择轮次少的速决战，后出价的买方当选择轮次多的持久战；（2）在偶数轮讨价还价中，先出价的卖方当选择轮次多的持久战，后出价的买方当选择轮次少的速决战；（3）不管是轮次少的速决战，还是轮次多的持久战，先出价的卖方都应选择奇数轮次讨价还价，后出价的买方都应选择偶数轮次讨价还价。

对商业实战的参谋部而言，可按照该算法的动态曲线来提供决策支持：（1）在沙盘模拟推演过程中，为做到“知己知彼，百战不殆”，既要演示均衡报价策略，也要演示均衡分配策略；既要报告卖方的均衡策略，也要报告买方的均衡策略。（2）在辅助司令部的战略决策方面，若司令部注重博弈的决策过程，则重点使用迭代算进行现场推演；若司令部注重博弈的决策结果，则重点使用递归算法进行现场推演。（3）在辅助作战部的战术决策方面，事前需充分挖掘以往讨价还价商业实战的大数据信息，借助博弈计量经济学，预估本次讨价还价的轮次将是多少和买卖双方的贴现因子各是多少。

对商业实战的作战部而言，可按照该算法的上下包络来做出战术决策：（1）作为卖方，不管博弈将要进行多少轮，可沿循均衡出价策略的上包络线依次降价，直到买方接受我卖方的出价为止。（2）作为买方，不管博弈将要进行多少轮，可沿循均衡出价策略的下包络线依次涨价，直到卖方接受我买方的出价为止。（3）在讨价还价过程中做好侦察与反侦察，不断获取对方出价行为的大数据，基于侦察到的后验信息，对对方贴现因子的先验估计予以贝叶斯修正；在沿着包络线依次出价的过程中，适当随机化，制造噪声，以此手段进行反侦察，可防对方过早得知我方的贴现因子。

6 结论

算法博弈论是博弈论与计算机交叉而成的一个新兴学科，其在商业智能时代有着广泛的应用需求。例如，在智能电子商务的讨价还价博弈中，买卖双方的均衡出价策略该如何求解。本文在求解动态博弈的基本思想，即逆向归纳法的基础上，开发出两个高效且实用的算法：迭代算法与递归算法。

基于逆向归纳过程，设计出迭代算法：（1）迭代的进程次序，一是由后往前逆向迭代，二是买卖双方交替迭代；（2）迭代的递推关系，轮到卖方（买方）出价时，买方（卖方）本轮所得份额是上轮所得份额的一次贴现，卖方（买方）获得对方贴现后的剩余份额。

基于逆向归纳结果，设计出递归算法：（1）递归的进程次序，由大到小，每次间隔两步，形成一条奇数递归路线和一条偶数递归路线；（2）递归的递推关系，既可采取卖方与卖方、买方与买方的自递归模式，也可采取卖方与买方、买方与卖方的交叉递归模式。

从算法的设计思路来看，迭代算法是逆向归纳法的具体实现；而递归算法并不拘泥于逆向归纳法，是一种全新的博弈求解思路。从算法的实验测试来看，这两个算法不仅高效、实用，还同时得出均衡出价策略的上下包络线。从算法的实际应用来看，算法所得均衡出价策略的上下包络线是买卖双方最优出价的控制线，这对设计电子商务智能出价系统至关重要。

基于此，本文还将电子商务的讨价还价实战分设司令部、参谋部、作战部等三个角色模块，给出应用该算法开发智能出价决策支持系统的初步设计思路为：司令部可按照该算法的上下包络来部署战略决策，参谋部可按照该算法的动态曲线来提供决策支持，作战部可按照该算法的上下包络来做出战术决策。