某航空发动机舱电子设备热设计

周 尧， 苗 力， 张丰华， 田 沣， 杨雨薇

(西安航空计算技术研究所， 西安 710119)

航空发动机直接影响飞机的整体性能，是一个国家科技工业水平和国防实力的重要标志。随着航空发动机在气动热力学和机械学方面不断发展，航空发动机推重比不断提高，燃油消耗明显降低。航空动力技术的不断进步使得飞机飞行速度不断提高，由亚声速提高到超声速，又由超声速提高到超声速巡航。下一代飞机具有高超声速、高智能等技术特性，对航空发动机性能提出了更高的要求[1-3]。高性能的发动机带来涡轮前温度的不断提高和热负荷的不断增加，且在高超声速飞行时，由于气动加热，飞机表面温度会随着马赫数的增加而快速升高[4]，造成发动机舱内热环境极为恶劣。

出于对发动机控制和状态监控的需要，航空发动机舱内安装有大量电子设备，这些设备使用的硅基电子元件对工作温度有严格要求，过高的温度会导致电子元件失效[5]，影响飞行安全，因此必须对发动机舱电子设备进行合理的热设计。然而，发动机舱内热量产生和传递过程十分复杂。热量通过辐射、对流和传导方式在发动机舱内部件间传递，并在传递过程中相互耦合。对电子设备与其所处的发动机舱热环境之间热量相互传递进行定量分析具有一定难度。

中外对于航空发动机舱热环境进行了大量研究。王杏涛等[6-7]对发动机舱通风冷却和遮挡隔热综合降温效果进行了研究，通过数值计算和实验研究了各种措施对于发动机舱蒙皮的降温效果。马松等[8]采用数值模拟方法研究了某型发动机舱温度场分布，并与试验结果进行了对比分析。李永林等[9]对飞机整机平台各部分环境温度进行了建模仿真研究。吴宇等[10]对某型飞机短舱辐射换热进行了数值计算研究。刘友宏等[11]对高速飞行器发动机舱热环境进行了研究，建立了估算发动机舱内元组件热环境的传热模型。刘友宏等[12]还基于数值模拟方法对某型组合发动机舱元组件热防护进行了初步研究。Antonio[13]对某飞机短舱温度场和换热特性进行了流固耦合传热分析。Watanabe[14]建立了航天器载货舱热环境模型，并将计算结果与实验数据进行了对比分析。

目前，对航空发动机舱热环境的研究主要以发动机、飞机蒙皮以及舱内空气温度场分布以及它们之间的相互影响为研究目标，得出的研究成果难以直接应用于航空发动机舱电子设备的热设计。在对发动机舱电子设备进行热设计时，往往只能将电子设备热环境的边界条件简化为舱内空气的温度场分布，而忽略了发动机、蒙皮作为辐射热源的影响。因此，本文针对某航空发动机和电子设备的具体参数和工况，研究了舱内电子设备与热环境间的热量传递情况，以为航空发动机舱电子设备热防护和热管理系统设计提供依据。

1 传热分析

涡扇发动机是目前应用最为广泛的飞机引擎之一，战斗机一般使用体积较小的小涵道比涡扇发动机。典型的小涵道比涡扇发动机舱结构如图 1所示。发动机在运行时内部会产生大量热量，其中一部分通过发动机机匣传递至发动机舱。发动机舱内安装有油泵、滑油箱、起动机等大量附件和设备，为了保证发动机舱内附件正常工作，一般是从机身的冲压口引入空气对发动机舱进行冷却。发动机舱最外侧由飞机蒙皮包裹，形成一个相对封闭的空间。

图1 发动机舱结构示意图Fig.1 Structure scheme of engine nacelle

作为一个流固耦合的热系统，发动机舱内部热量产生和传递过程十分复杂。根据刘友宏等[11]的研究，对于舱内电子设备热分析，可以按照各个因素影响力的大小进行划分，把这些因素划分为强影响和弱影响因素，在进行热分析时忽略弱影响因素，仅考虑强影响因素。对电子设备换热影响较大的3组因素分别为：发动机机匣壁面温度分布、蒙皮内侧壁面温度分布和发动机舱内空气温度分布。发动机机匣壁面与蒙皮内侧壁面主要通过辐射方式与电子设备换热，而发动机舱内空气主要是通过对流方式与电子设备换热。相对于发动机、蒙皮的热流，电子设备本身的发热量较小，对于发动机舱热环境影响可以忽略。

在本文中，主要关注电子设备与环境之间的换热情况，而上述3组因素之间的相互影响关系并不是电子设备热设计需要考虑的主要问题。因而，本文把上述3组环境因素的状态视为已知条件。实际上，不同类型发动机或者在发动机不同的运行状态下，发动机机匣壁面温度分布情况变化很大，蒙皮内侧壁面温度分布情况也是如此。然而，由于电子设备通常体积较小以及发动机舱几何形状的限制，能够与电子设备进行辐射换热的表面主要集中在电子设备安装处附近的发动机机匣壁面、蒙皮内侧壁面较小区域内，在该较小区域内可以视为发动机机匣壁面和蒙皮内侧壁面的温度是均匀分布的。由于发动机舱内安装有大量管路和保障发动机运转的附件，几何形状复杂，电子设备附近的空气流动状态难以准确获知，但由于其他设备对空气流动的阻挡，以及发动机舱相对密闭的状态，本文将电子设备外表面与空气之间的换热视为自然对流。此外，由于发动机舱内温度较高，通常需要对电子设备进行热防护和散热设计，热防护措施即在电子设备外部设计一定厚度的隔热材料，减少外部热量向电子设备内部传递，而散热方式一般是引入其它冷源如低温空气或燃油带走电子设备内部热量，将电子设备元器件维持在合适的温度。

除了上述分析，为了建立发动机舱电子设备与周围环境的换热模型，还需进行以下假设：发动机处于稳定工作状态，发动机舱及电子设备已达到热平衡。

2 计算模型

以某航空发动机为例，主要的几何尺寸见图 2所示。某电子设备安装于发动机下方，其外部设计有一定厚度的隔热材料，并且引入燃油进行冷却以控制内部温度，如图 3所示。当发动机舱和电子设备达到热平衡状态后，由于电子设备接收到辐射热Фr，其外部隔热材料表面温度升高，通过对流方式将一部分热量Фh散发到空气中，另一部分热量Фc通过隔热材料传递至电子设备内部。进入隔热材料内部的热量Фc最终由燃油或其他介质转移出发动机舱热系统。

图2 发动机舱尺寸示意图Fig.2 Structure scheme of engine nacelle dimensions

图3 电子设备传热示意图Fig.3 Structure scheme of electronic device heat transfer

根据上述分析可知各部分热量存在关系：

Φr=Φh+Φc

(1)

首先，考虑隔热材料外表面通过对流方式散发到发动机舱空气中的热量Фh。

根据自然对流传热的实验关联式，隔热材料外表面可分为3类：水平热面朝上、水平热面朝下和竖平板。对于各表面，其对流散热量为

Φhi=AihiΔti

(2)

式(2)中：Ai为各个面的面积；hi为各个面对流换热系数；Δti为各个面与空气的温差。

对流换热系数可根据式(3)计算：

(3)

式(3)中：Nui为努赛尔数；λa为空气导热率；li为特征长度，即面积除以周长。

对于水平热面朝上的情形，努赛尔数根据式(4)计算：

(4)

式(4)中：Gr为格拉晓夫数，Pr为普朗特数，可根据空气热物性表查得。

对于水平热面朝下的情形，努赛尔数根据式(5)计算：

Nu=0.27(GrPr)1/4

(5)

对于竖面，努赛尔数根据式(6)计算：

Nu=0.59(GrPr)1/4

(6)

格拉晓夫数根据式(7)计算：

(7)

式(7)中：g为重力加速度；αv为体胀系数；ν为空气运动黏度。

其次，考虑隔热材料外表面通过传导方式进入内部的热量Фc。实际上，隔热材料外部热量主要通过传导和辐射方式进入内部，为了便于计算，此处将通过辐射方式进入内部的热量统一整合到传导热量Фc中，在原本的隔热材料导热率λ中加入辐射因素后形成的等效导热率λe来实现这一整合，等效导热率λe可由试验测得。

由隔热材料外表面传递至电子设备的热量为

(8)

式(8)中：A为隔热材料垂直于传热方向的截面积；Δtc为隔热材料内外表面的温差；L为隔热材料厚度。

最后，考虑电子设备外部隔热材料接收的辐射热Фr。

该部分热量的来源主要是发动机机匣表面、蒙皮内表面以及电子设备周边固体表面，虽然在高超声速飞行时蒙皮内表面温度很高，但此类飞行器往往在蒙皮内部设置隔热措施以降低温度，故实际内表面温度通常接近发动机舱内空气温度，电子设备周边固体表面温度通常也与舱内空气温度相差不大。根据波尔兹曼定律，辐射换热量与辐射源温度的四次方成正比，因此电子设备外部隔热材料接收的辐射热Фr主要来自温度显著高于其他表面的发动机机匣表面，在分析中忽略其他表面的辐射热。

如图4所示，根据发动机舱的尺寸和几何形状经计算可知，在发动机轴向方向上，距电子设备几何中心处水平距离1 000 mm处的发动机机匣表面对于电子设备的辐射角系数小于0.07，而在径向方向上，距电子设备几何中心处水平距离400 mm处的发动机机匣表面对于电子设备的辐射角系数小于0.06。据此，可以认为在该范围外的发动机机匣表面对于电子设备无辐射换热作用。

在实际环境中，发动机壁面发出的辐射热量主要被发动机蒙皮和其他表面吸收，可以将蒙皮和其他表面视为黑体表面。为了使问题能够求解，将电子设备面与发动机机匣有效区域面通过虚构面封闭起来，机匣有效区域面1、电子设备外表面2及虚构面3构成一个封闭的腔体，虚构面3为温度恒定的黑体表面。虽然机匣有效区域面1为弧形曲面，但在辐射换热分析中，该曲面与相同大小平面的作用相同，故将其简化为平面。简化后的发动机与电子设备辐射换热模型如图 5所示。

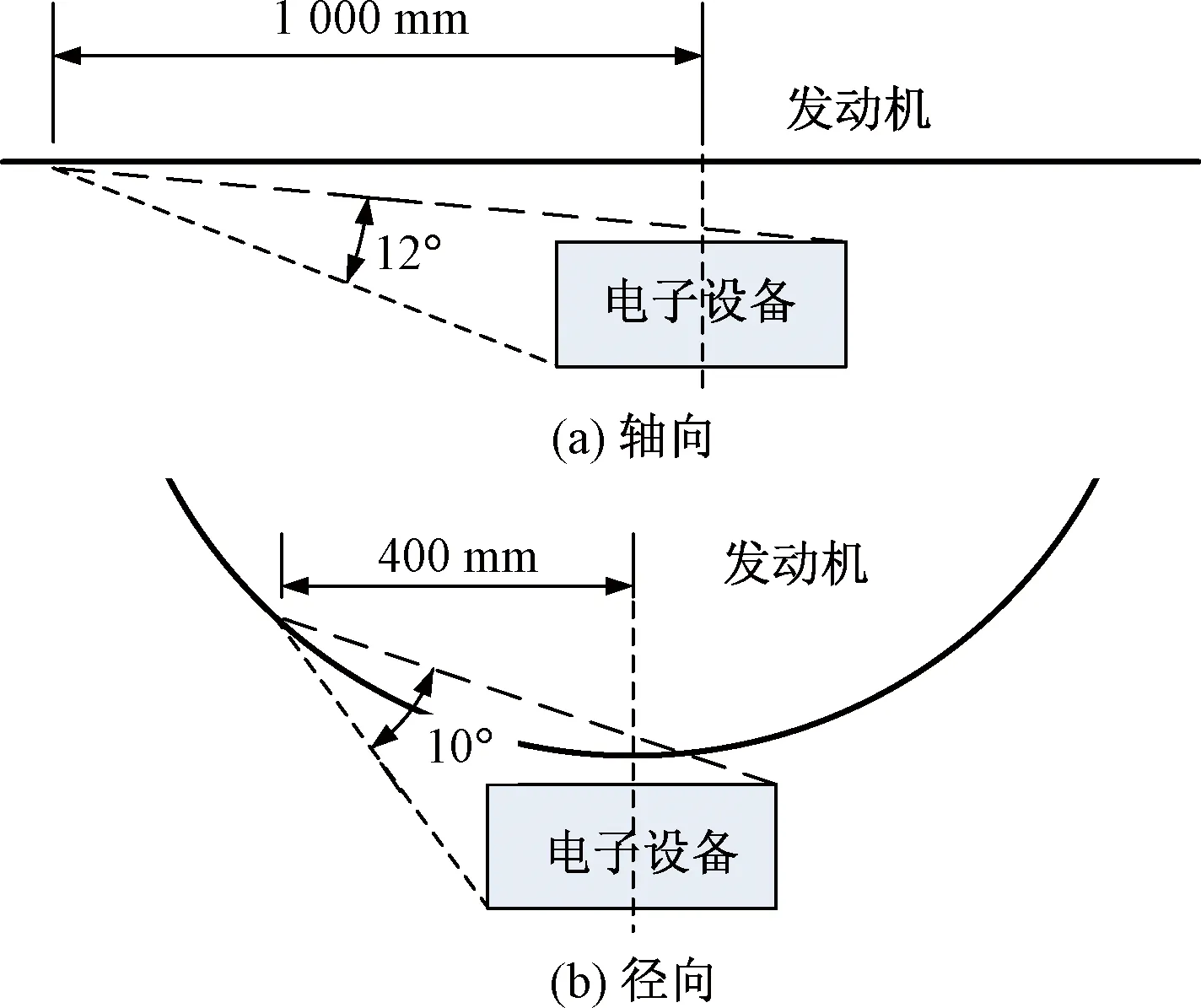
图4 电子设备位置示意图Fig.4 Structure scheme of electronic device position

图5 简化辐射传热模型Fig.5 The model of simplified radiation heat transfer

面1到面2的角系数表达式为

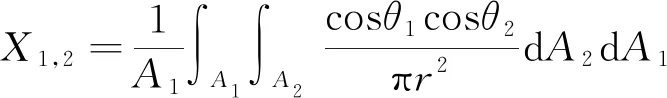
(9)

式(9)中：A1、A2分别是面1和面2的面积；dA1、dA2是两个表面上的微元面；r是两微元面的距离；θ1、θ2分别是微元面dA1、dA2与两微元面连线的夹角。

上述四重积分的求解过程较为复杂，此处不再详细叙述。可得面1到面2的角系数：

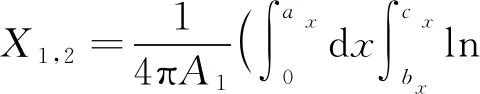
(10)

面1到面3和面2到面3的角系数分别为

X1,3=1-X1,2=0.938 1

(11)

X2,3=1-X2,1=0.009 6

(12)

对图5所示的简化辐射换热模型可列出以下方程：

(13)

式(13)中：J1、J2分别为面1、面2的有效辐射；Eb1、Eb2分别为面1、面2的黑体辐射力；ε1、ε2分别为面1和面2的发射率。

表面黑体辐射力的计算公式为

(14)

式(14)中：σ为黑体辐射常数；t为表面的温度。

表面的有效辐射的计算公式为

(15)

式(15)中：q2为面2的净辐射换热量，即面2在辐射换热中能量收支差额。

因此，电子设备外部隔热材料接收的辐射热的计算公式为

Φr=q2A2

(16)

至此，发动机舱电子设备传热模型已经建立，发动机舱几何尺寸、空气及各种材料的物性参数为已知参数，如前所述发动机机匣温度、蒙皮温度以及发动机舱空气温度为已知，上述参数在该模型里作为边界条件输入模型，隔热材料内表面温度即电子设备设计目标工作温度也为已知，而模型的输出结果主要是隔热材料外表面温度以及传入电子设备的热量。联立式(1)、式(2)、式(8)及式(16)，采用牛顿迭代法编写MATLAB计算程序可以对模型进行求解。模型计算的主要参数如表 1所示。

表1 主要参数

3 计算结果

当发动机机匣表面温度为673 K，隔热材料表面发射率为0.8，其他参数如表1所示，不同发动机舱空气温度时的隔热材料表面温度、各部分传热量值分别如图 6、图 7所示。可见，隔热材料表面温度随着发动机舱空气温度升高而升高，但前者升高速度较后者速度慢。随着发动机舱空气温度升高，传导热量缓慢上升，而辐射热量、对流热量均有所降低。

当发动机机舱空气温度为473 K，隔热材料表面发射率为0.8，其他参数如表 1所示，不同发动机机匣温度时的隔热材料表面温度、各部分传热量值分别如图 8、图 9所示。可见，随着发动机机匣温度升高，隔热材料表面温度快速上升，同时各部分传热量值均增大。与发动机舱空气温度相比，发动机机匣温度对于传入电子设备内部的热量值影响较大。

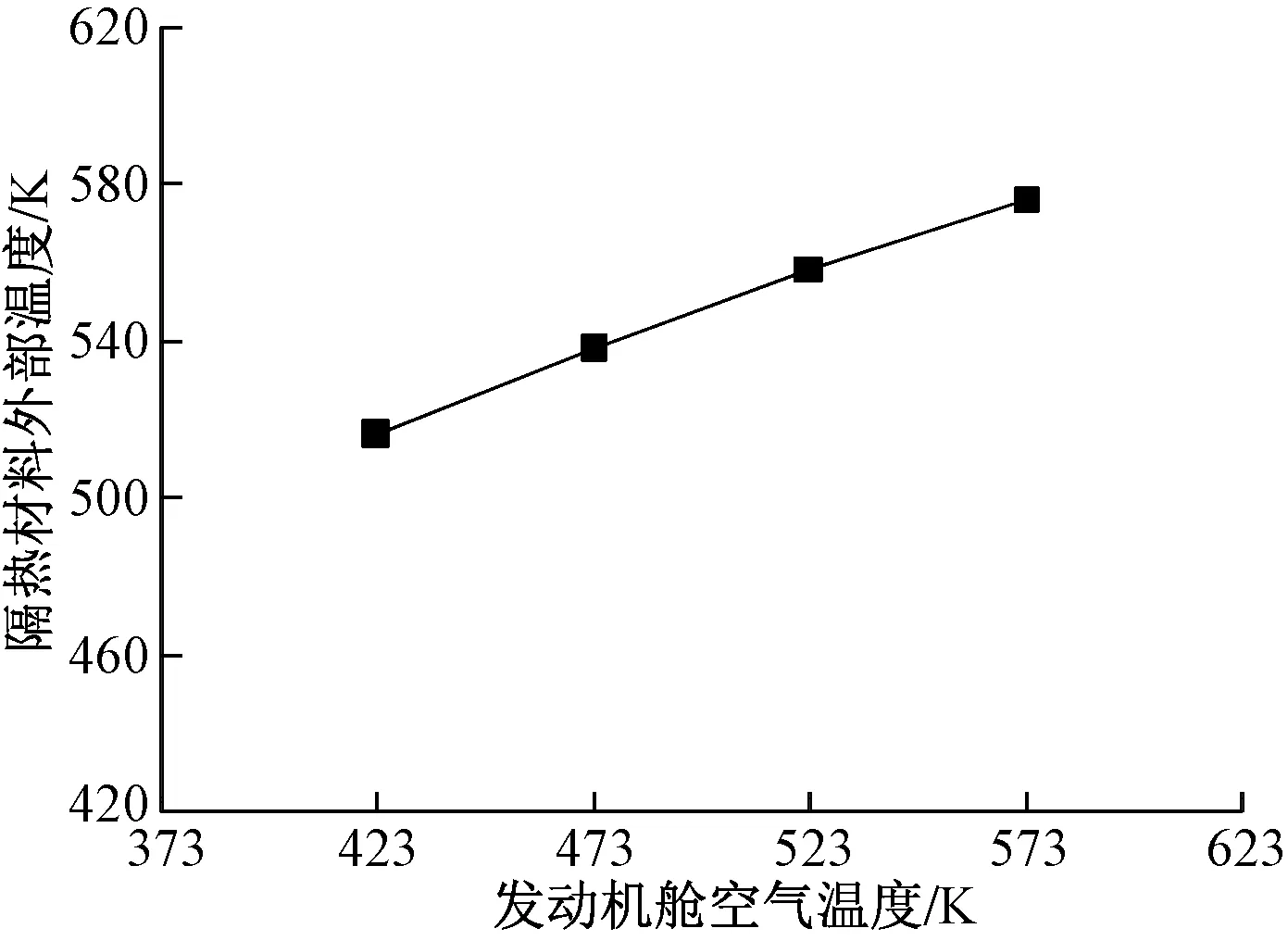
图6 不同空气温度时的隔热材料表面温度Fig.6 Surface temperature of insulation material at different air temperature

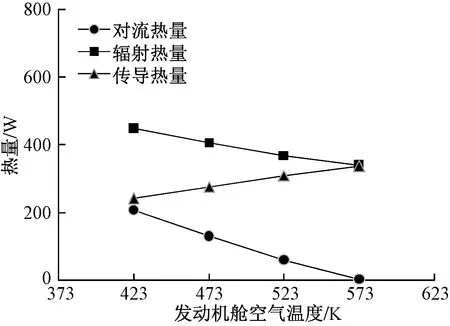
图7 不同空气温度时的传热量值Fig.7 Heat transfer value at different air temperature

图8 不同机匣温度时的隔热材料表面温度Fig.8 Surface temperature of insulation material at different case temperature

当发动机机匣表面温度为673 K，发动机机舱空气温度为473 K，其他参数如表 1所示，不同隔热材料表面发射率时的隔热材料表面温度、各部分传热量值分别如图 10、图 11所示。可见，在其他条件相同时，隔热材料表面的发射率越高，隔热材料表面的平衡温度也越高，传入内部的热量越大。

图9 不同机匣温度时的传热量值Fig.9 Heat transfer value at different case temperature

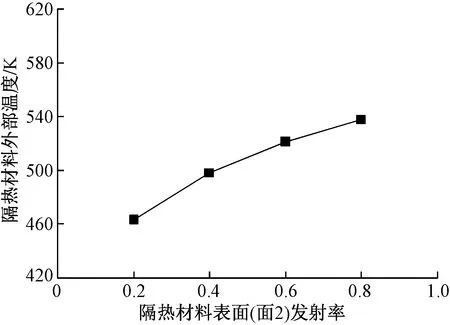
图10 不同发射率的隔热材料表面温度Fig.10 Surface temperature of insulation material with different emissivity

图11 不同发射率的传热量值Fig.11 Heat transfer value at different emissivity

4 结论与分析

针对某航空发动机和电子设备的具体参数和工况，研究了舱内电子设备与热环境间的热量传递情况，得出以下结论。

(1)通过对发动机舱内部热量产生和传递过程进行分析，得出了电子设备达到热平衡时的平衡方程，建立了发动机舱电子设备传热计算模型。

(2)环境传递到电子设备的热量主要是来自于电子设备附近较小范围内的发动机机匣表面辐射热。

(3)与发动机舱空气温度相比，发动机机匣温度对于传入电子设备内部的热量值影响较大。

(4)隔热材料表面发射率越高，隔热材料表面的平衡温度也越高，传入电子设备内部的热量越多。