山区风电临坡圆形基础倾覆失稳对坡体变形的影响

李大勇, 梁 昊, 张雨坤*

(1.山东科技大学山东省土木工程防灾减灾重点试验室， 青岛 266590； 2.福州大学土木工程学院， 福州 350108)

面对日益严峻的环境问题，可再生能源的开发与利用受到全球的重视，在各类新能源开发中，风能资源的开发利用得到了广泛关注。截至2016年底，全球风电和新增装机容量超过10 GW,累计容量达到468.8 GW,累计装机容量增长12.6%，中国风电累计和新增装机容量均居全球第一[1]。由此可见，中国风电行业发展迅猛，风能已经成为重要的清洁能源之一。

随着中国陆上风电产业及相应技术的快速发展，风电场建设范围越来越广。山区地带蕴藏着巨大的风能且风速远高于平原地带，极大提高了风电场的发电效率[2]，因此，许多风电场在山区地带进行选址，并把基础设置在山坡坡顶。然而，在坡顶建设风电基础既要保证基础和上部结构长期安全运行，同时要保证山坡的稳定性。因此需要深入研究山区风电基础对山坡稳定性的影响。

目前，边坡稳定性研究主要采用以下几种手段：①原位试验及现场检测：通过施工过程中对临坡基础进行实时检测，及时掌握边坡整体形变[3]；②数值模拟试验：在室内试验条件下确定岩土体参数，运用数值模拟得到不同工况下边坡变形的破坏特征[4]；③室内模型试验：将实际工程按照一定比例缩制为试验模型，得到不同工况下试验模型变形、破坏特征[5]。基于这些方法，中外学者对边坡问题展开研究。Choudhury 等[6]根据斜坡地基的破坏形式，提出了三种不同的滑动面模式，并针对每种滑动面提出了相对应的判别条件。Ghosh等[7]采用极限分析上限法，研究基础位于边坡上时，水平地震加速度的变化对承载力系数Nc、Nγ的影响。赵建军等[8]通过室内模型试验探讨工程荷载作用下填方边坡变形破坏机制，发现模型平台在堆载后呈现明显不均匀沉降，平台的右侧与后侧沉降量较大。唐胜传等[9]研究了边坡稳定性系数与最大水平位移之间的关系，发现临坡距为0、4 m可采用幂函数进行拟合，临坡距为14 m使用线性函数拟合较好。李震等[10]分析了不同临坡距、相对密实度、基底宽度的基础荷载-位移曲线，研究了极限承载力、极限承载力弱化系数、极限承载力系数的多因素演化规律。蒋洋等[11]采用数值模拟分析了地基土强度、边坡角、临坡距、基地接触条件等因素对临坡地基极限承载力的影响，为计算临坡地基极限承载力提供了依据。侯超群[12]研究了斜坡地基的变形规律和破坏特征，得出斜坡地基破坏呈非对称性，应力向倾斜的一侧集中，临坡地基因应力集中而先达到极限平衡状态，破裂面相交于坡面中下部。胡卫东[13]为了研究临坡地基的滑动变形形态、土压力分布特征、破坏模式及极限承载力，采用在特制地槽内填筑土石混填临坡地基，进行条形基础地基模型的竖向静载试验研究。

开展数值模拟，研究了临坡圆形基础倾覆失稳、基础临坡距离等对坡体变形的影响，得到了圆形基础临坡安全距离。然后，对圆形基础在临坡地基上位移云图及矢量位移图进行分析，研究了边坡角对坡体变形的影响规律。最后研究了基础失稳过程中，临坡距对基础埋深方向转动点的影响，为现场施工提供一定的参考依据。

1 有限元模型

运用ABAQUS软件进行数值模拟，圆形基础模型如图1所示，具体的基础模型尺寸见表1，模拟一共采用五种圆形基础尺寸，并对其进行编号，以“D26H6”为例，①D为圆形基础直径，数字“26”表示基础直径260 mm；②H为圆形基础高度，数字“6”表示基础高度60 mm。

考虑到圆形基础结构具有对称性，为节省计算时间，取基础与地基的一半进行分析，有限元网格划分如图2所示。为消除边界效应的影响，取临坡地基在高度方向为基础高度的5倍，在水平方向为基础直径的7倍，宽度方向为基础半径的5倍，如图3所示。数值模拟中主要设置2个分析步：第一个为生成初始应力分析步，第二个为加载步，采用位移控制式加载方式，对圆形基础施加水平位移。

地基土为中密砂土，砂土参数通过室内试验确定，服从Mohr-Coulomb屈服准则，圆形基础由钢材制作而成，采用线弹性模型，砂土及圆形基础力学参数如表2所示。圆形基础与地基土之间设置为摩擦接触，其摩擦系数μ=0.46。为验证模型试验准确性，对圆形基础进行水平加载，将数值模拟与模型试验结果对比，如图4所示，结果表明在不同临坡距(e/D)下，数值模拟与模型试验吻合性较好。

图1 圆形基础Fig.1 Circular foundation

表1 圆形基础尺寸

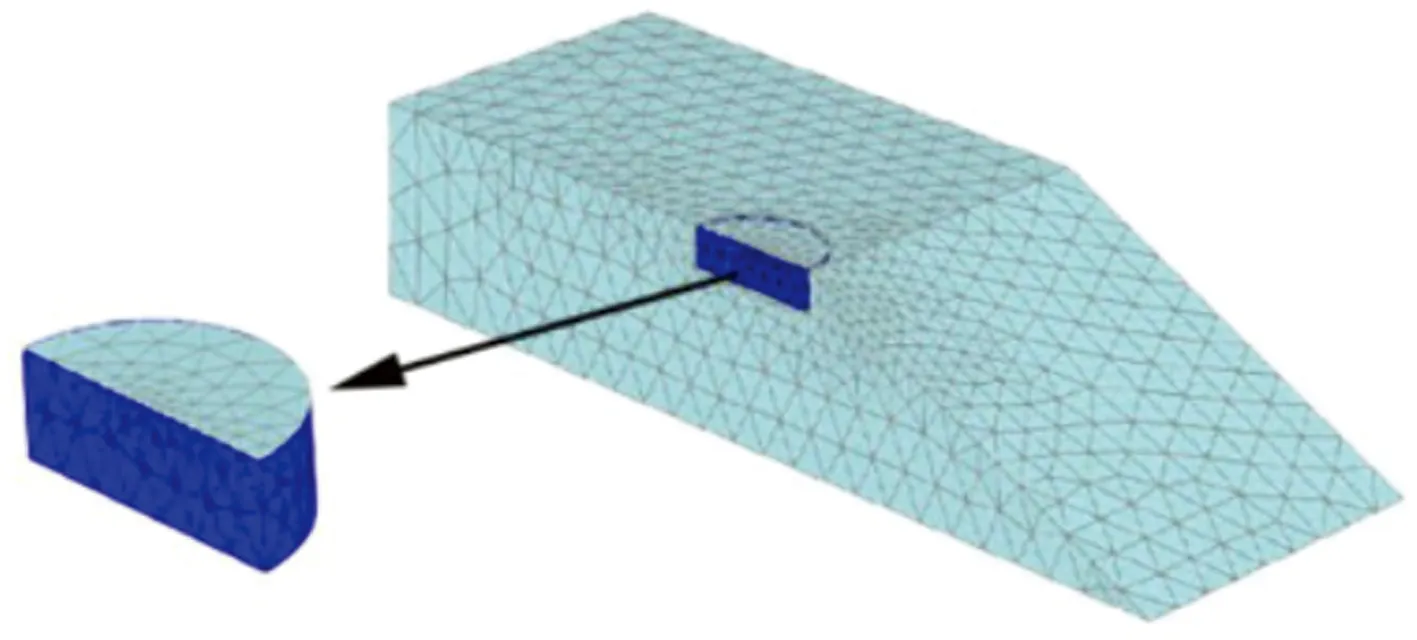
图2 有限元网格划分Fig.2 Finite element mesh generation

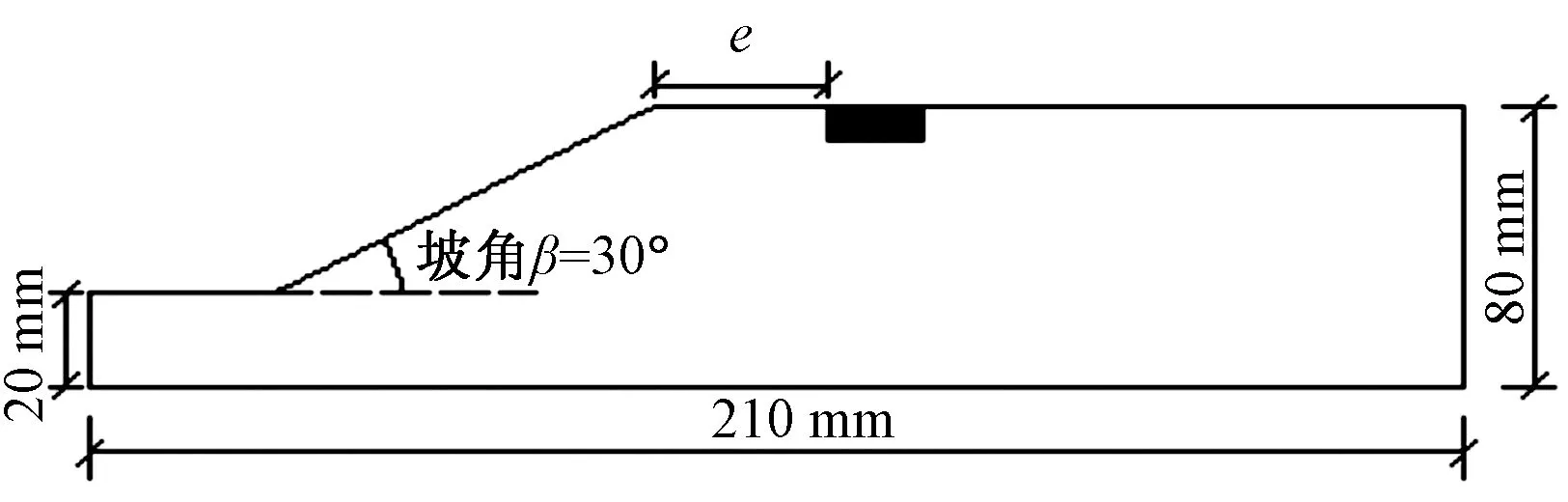
e为基础到边坡的距离图3 临坡地基的几何尺寸示意图Fig.3 The geometric dimension diagram of the finite element model

表2 材料参数设置

图4 数值模拟与试验结果对比Fig.4 Numerical simulation and test results

2 结果与分析

2.1 临坡距对边坡变形的影响

图5所示为不同直径圆形基础在5种临坡距条件下，倾覆失稳时坡面隆起变形沿垂直方向的变化规律。从图5中可知坡面隆起随着临坡距的增大呈减小趋势，基础尺寸一定的条件下，当e/D=3时，坡面隆起达到最大，这是因为随着临坡距不断增大，由外荷载产生的附加应力对边坡影响逐渐减小，从而使坡面隆起不断减小。e/D一定时，坡面隆起在坡顶位置位移最大，即边坡最大隆起值，且坡面隆起在坡体上随着距坡顶距离增大而减小，直至不发生坡体隆起。e/D=10～20时，坡面隆起趋近于0，表明基础在此距离对边坡的影响作用较小，被认为处于安全距离之内，此时可视临坡地基近似为水平地基。

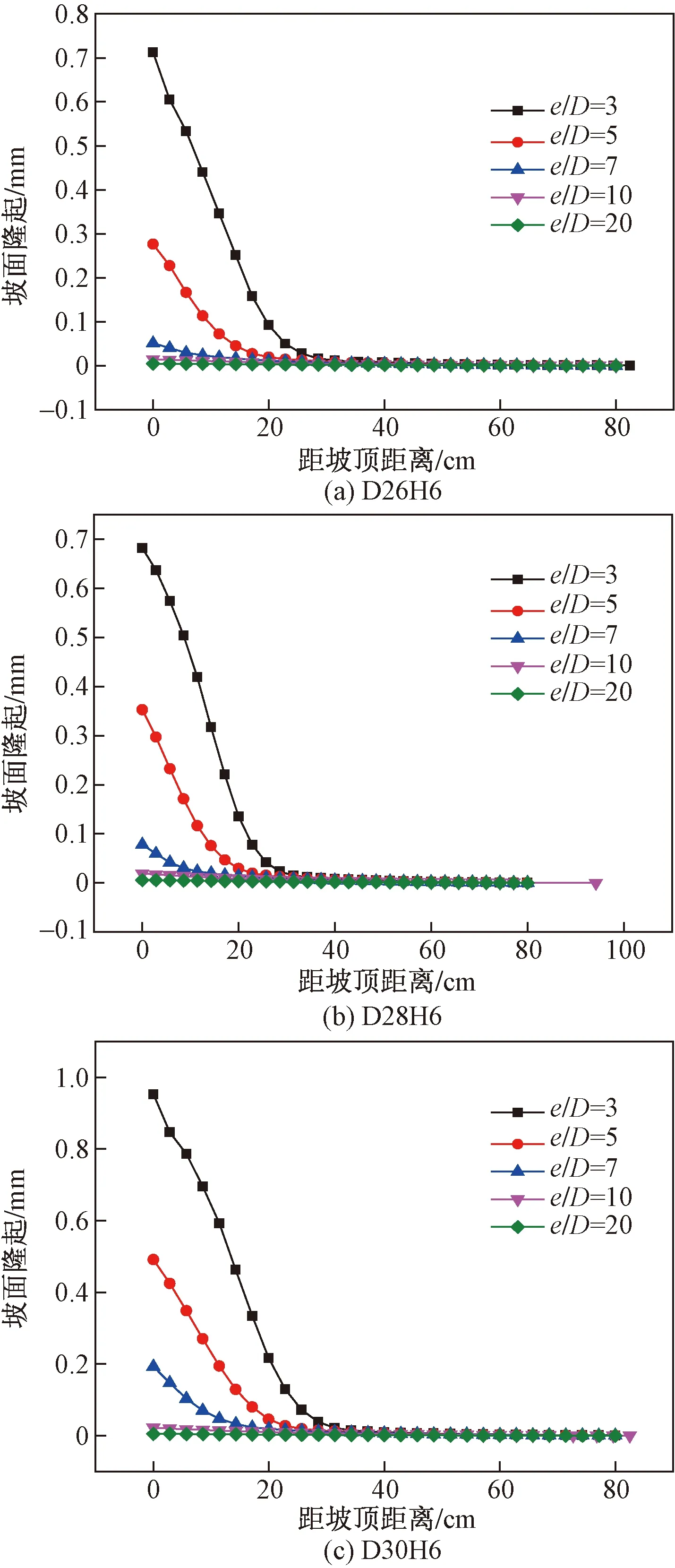
图5 圆形基础失稳时坡面隆起变形沿垂直方向变化规律Fig.5 Deformation of the slope surface under the failure of the circular foundation

图6给出不同基础直径(D26H6、D28H6、D30H6)下的坡面最大隆起，通过对比可知，在相同临坡距下，最大隆起随着基础直径增大而增大，以e/D=3情况为例，圆形基础D30H6的坡面隆起最大，较D28H6和D26H6分别提高了46%和50%，因为基础直径增大以后，基础对土体的调动范围扩大，所以影响范围内的土体最大隆起有所提高。e/D=10～20，3种基础直径下边坡的最大隆起都趋近于0，由此看出增大基础直径不影响圆形基础与边坡的安全距离。

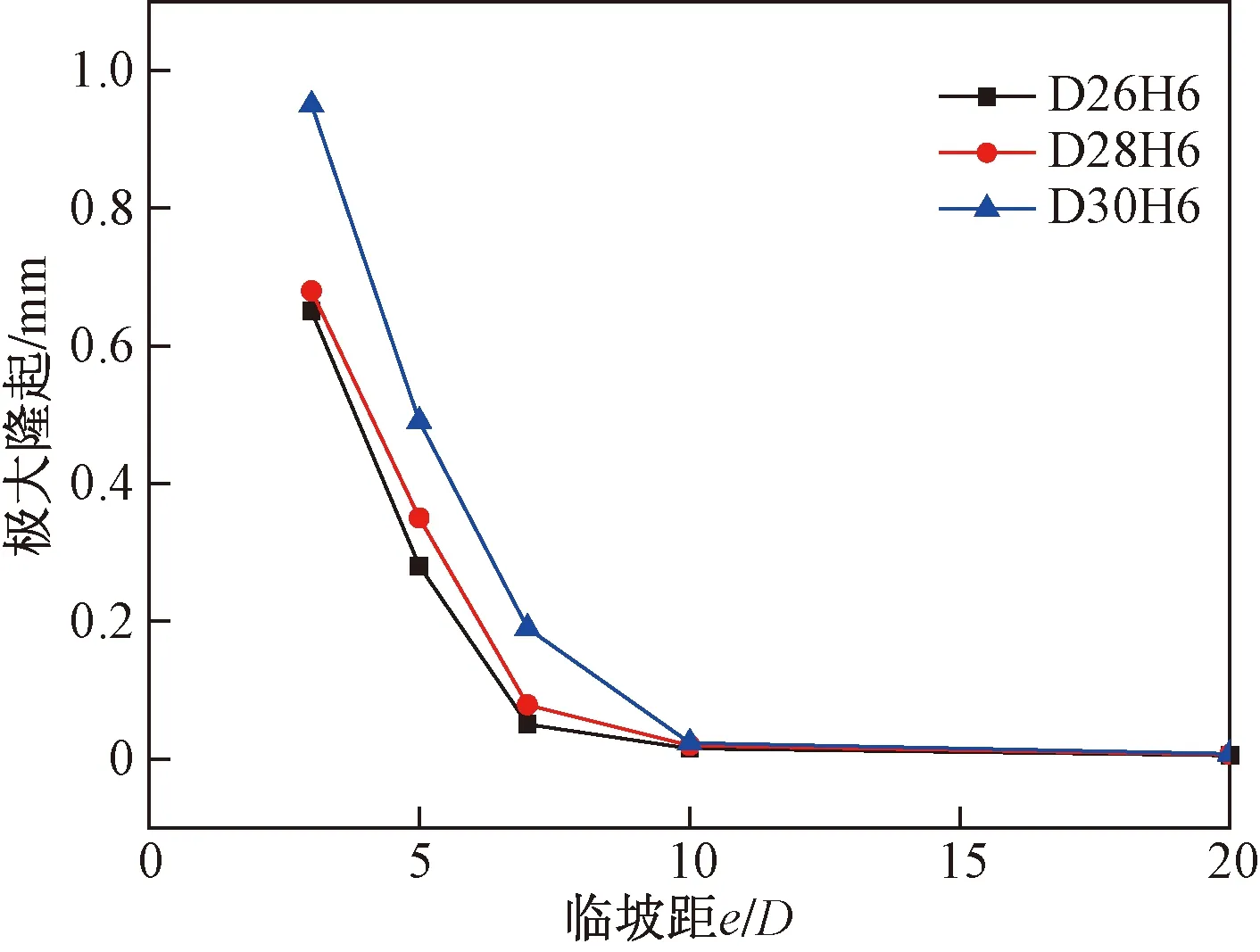
图6 基础直径对坡体变形的影响(β=30°)Fig.6 Influence of base diameter on slope deformation (β=30°)

2.2 临坡地基的变形分析

对尺寸为D26H6的圆形基础进行分析，当e/D=3时，得到边坡位移云图及矢量位移如图7所示。圆形基础倾覆失稳后，位移云图中形成穿过坡面的圆弧滑动面，临坡地基最大应变出现于坡顶位置，随着距离不断增大，坡面应变不断减小，其影响范围约为基础直径的10倍，通过位移云图进一步验证了2.1节结论。由图7(b)可以看出，基础下方土体沿加载方向向斜下方移动，而基础前侧土体沿加载方向向斜上方移动且土体在坡顶位置产生一定范围隆起。

图7 D26H6基础位移云图及矢量位移图Fig.7 Deformation contour and vector displacement of the foundation of D26H6

2.3 边坡角对边坡的影响

为了进一步研究临坡基础对坡体变形的影响，图8给出基础D26H8在边坡角30°和45°时，坡面隆起值—距坡顶距离的关系曲线。由分析可知：当边坡角为45°时，与坡角30°相比，其坡面隆起出现大幅度提高且边坡影响范围急剧增大，e/D=3、5、7的三条曲线最大隆起分别提高70%、114%、171%，且曲线末端出现陡降，说明基础对边坡的影响范围达到了整个坡面。因为对于无黏性土坡来说，随着边坡角增大，土体有沿坡面下滑的趋势，从而在附加应力的作用下，边坡变形将会增大，因此，增大边坡角对边坡稳定性将会产生不利的影响。当e/D=10、20时，两种边坡角的坡面隆起量与影响范围变化非常微小，处于安全距离之内，由此说明改变边坡角不会对安全距离产生较大的影响。

图8 不同边坡角下边坡变形的关系曲线Fig.8 Relation curve of slope deformation at difficult slope angles

图9 基础在埋深方向各测点的测移Fig.9 Fundamental movement of measurement points at the foundation

2.4 不同临坡距对基础埋深方向转动点的影响

为了了解基础在临坡地基上的运动规律，图9给出不同临坡距下D28H8基础前侧沿埋深方向各测点的位移量，图9中各曲线与y轴(侧移为0)的交点即为转动点沿深度方向的位置。如图9所示，以e/D=3为例进行说明，随着荷载的增加，各测点发生不同程度的向右移动且所连直线的斜率逐渐减小，说明基础在发生平动的过程中产生一定的转动。

此外，从图9中还可以看出，e/D=3、5、7、10、20时，转动点的变化规律整体上呈现先上升后下降的趋势。这是因为基础有平动和转动两种运动模式，转动点上升阶段基础的运动模式主要以转动为主，从而使测点的斜率不断降低，与侧移为0的直线交点上移。而转动点下降阶段可以理解为基础运动模式以平动为主，测点的斜率逐渐提高，导致基础沿埋深方向上转动点的位置下移。

3 结论

主要研究了临坡圆形基础对边坡变形的影响，运用ABQUES进行数值模拟试验，研究了临坡距、基础直径、边坡角对边坡变形的影响规律，并且进一步研究圆形基础转动点的变化规律。得出以下结论：

(1)随着临坡距的增加，圆形基础对坡面的影响逐渐减小，以基础D26H6为例，e/D=3时较e/D=5最大隆起增大了143%；临坡距e/D=10～20时，圆形基础对坡面扰动较小，e/D=10为圆形基础的参考安全距离。

(2)临坡距e/D为3、5、7时，增大基础直径使得坡面隆起显著提高，例如在e/D=3处，圆形基础D30H6的坡面隆起最大，较D28H6、D26H6分别提高了46%、50%；增加边坡角不仅使得坡面隆起增大且对坡面影响范围产生较大影响；临坡距大于10时，最大隆起均趋近于0，这表明临坡地基的安全距离没有较大影响。

(3)随着临坡距增加，圆形基础转动点呈先上升后下降的趋势，说明基础的运动方式由转动逐渐转为平动为主。