高速列车半主动悬挂系统的振动及主动控制

赵艳影， 黄小卫

(南昌航空大学飞行器工程学院， 南昌 330063)

在中国铁路高速化的背景下，列车运行速度不断提高。随着列车的提速，车辆的振动性能不断恶化。目前对高速列车减振技术的研究主要集中在车辆系统动力学、半主动悬挂系统控制律、半主动悬挂系统减振器三个方面。对车辆系统动力学的研究主要集中研究非线性轮轨接触[1]、动力学分岔[2]、蛇形动力学行为[3]、动力学仿真模型[4]、悬挂系统参数设计等[5]几个方面。现代车辆正朝着安全、舒适的方向发展，因轨道不平顺导致的车体振动引起了学者们的关注，悬挂系统智能化解决了传统被动悬挂存在的舒适性和稳定性不能兼顾的问题。主动悬挂系统是在悬挂系统中加入受控作动器，以抑制车体的振动[6]。虽然主动悬挂性能最优，但是也存在内部结构复杂、成本高、耗能高等问题，尤其重要的是不能控制在悬挂失效时的稳定性，这些缺陷导致其在实际列车上应用不多。针对主动悬挂系统的缺点，半主动悬挂因其结构大大简化以及控制效果良好等优势应运而出[7]。时间滞后，简称时滞，是系统中存在的时间延迟现象，所有的控制系统中不可避免地存在时滞现象[8]，它可以在信号的测量、采集、传递等过程中，也可以存在于目标的反应过程中。针对半主动悬挂系统中的时滞问题，目前得到的一般结论是：时滞对控制系统具有显著的恶化影响[9]，从而提出了时滞研究的必要性[10]。这种恶化影响主要体现在时滞对车辆运行平稳性[11]、蛇形运动稳定性和随机振动响应[12]等，针对车辆系统动力学性能的仿真[13]研究也证实了时滞是半主动悬挂系统的不利因素。采用合理的控制律进行时滞补偿或时滞消除的方法，可以减小时滞对系统的影响，一般都能够使得控制系统得到明显改善。然而，研究也发现，时滞对车辆悬挂系统动力学行为的影响不是一成不变的，在某些时滞的区间内，时滞的存在能够改善悬挂系统的性能[14]，通过对控制参数进行优化，能够有效降低车身加速度[15]，从而提供了利用时滞的可能。本文及文献[16]对两自由度高速列车半主动悬挂系统的垂向振动进行研究，考虑了二系悬挂中的刚度三次非线性，重点讨论时滞反馈控制对车体振幅的影响规律，从而能够利用时滞改善悬挂系统的振动特性。

1 悬挂系统的控制微分方程

图1是高速列车半主动悬挂系统垂向振动的动力学模型。

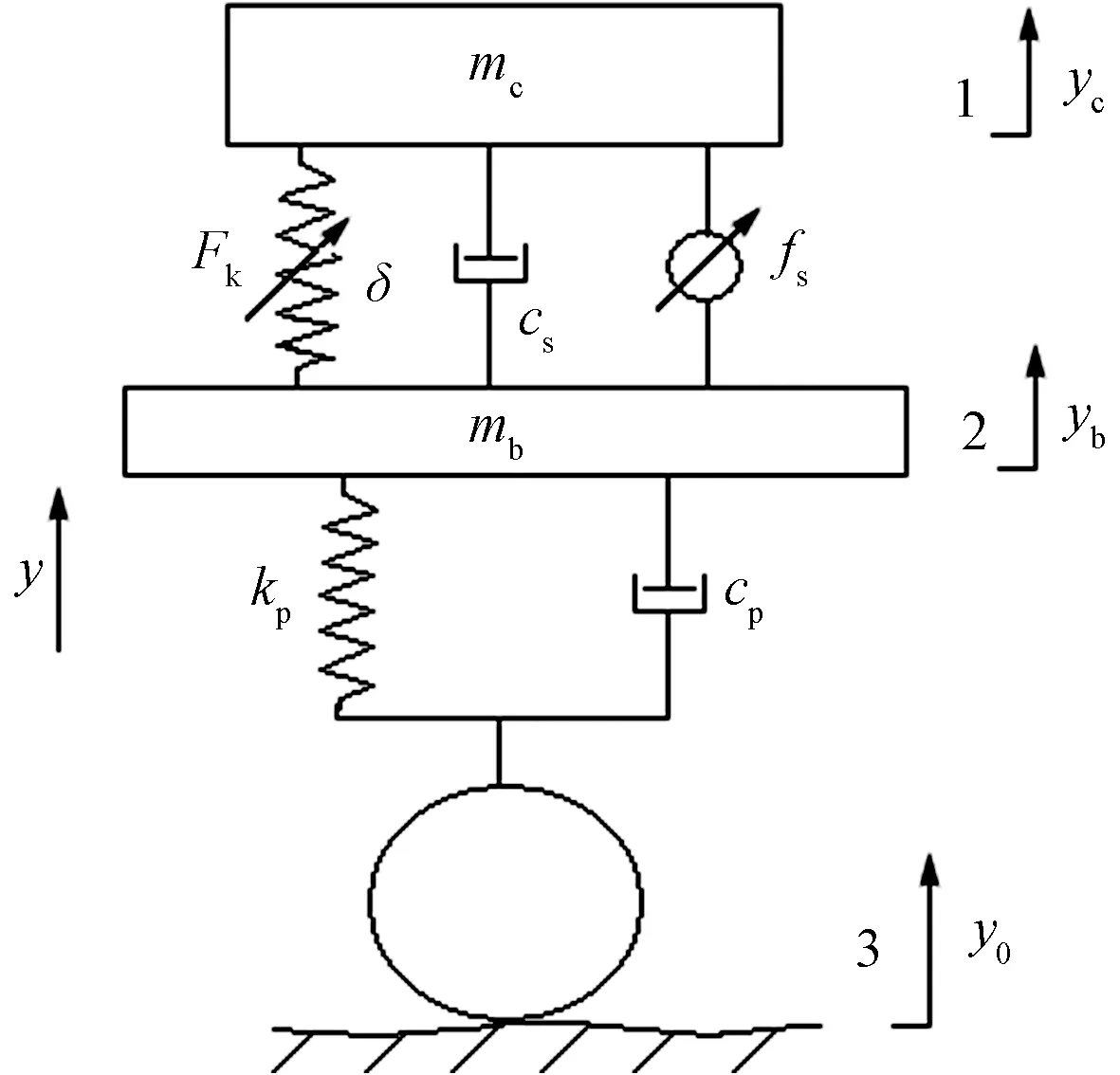
图1 高速列车半主动悬挂系统垂向振动模型Fig.1 Vertical vibration model of semi-active suspension system of high-speed train

ks[yb(t)-yc(t)]-δ[yb(t)-yc(t)]3=0

(1)

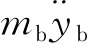
kp[y0(t)-yb(t)]+ks[yb(t)-yc(t)]+

δ[yb(t)-yc(t)]3=0

(2)

式中：yb和yc分别表示转向架和车体的位移；y0表示轨道不平顺激励，将其简化为简谐外激励的形式：y0=Fcos(Ωt)，F为外激励振幅，Ω为外激励频率。当fs=0时，反馈控制项消失，振动系统退化为非线性的被动控制系统。当τ=0时，时滞反馈控制项消失，振动系统退化为非线性主动无时滞反馈控制系统。

高速列车悬挂系统的物理参数参照CRH5选取，如表1所示。

表1 悬挂系统物理参数

2 线性系统的幅频及减振特性

首先，不考虑非线性因素，分析线性系统的振动特性。图2分别给出了线性被动减振系统(即fs=0，τ=0，δ=0)，在不存在阻尼和存在阻尼两种情况下垂向振动的幅频响应曲线，其中外激励振幅选择为F=40 mm。

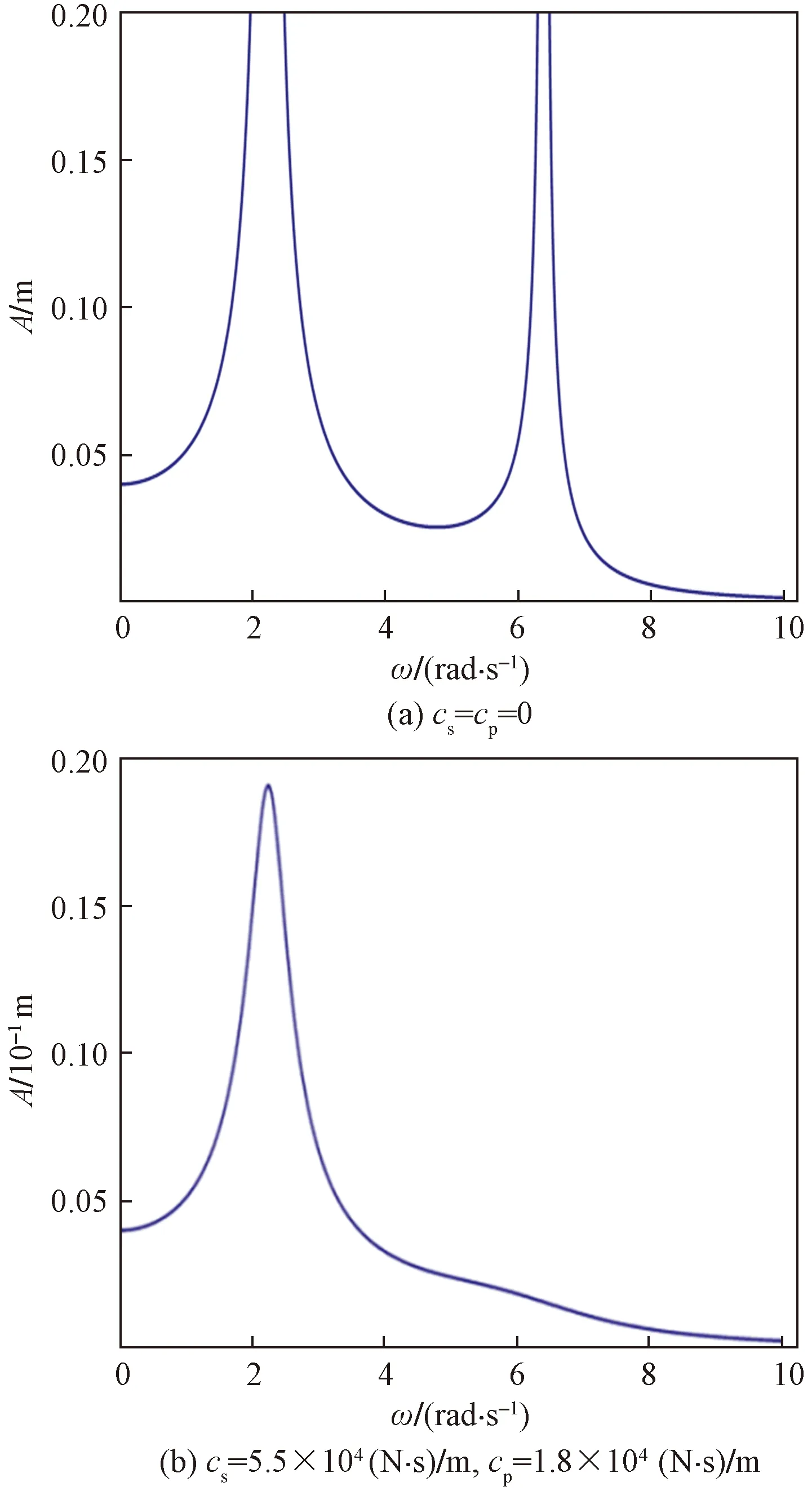
图2 车体的幅频响应曲线Fig.2 Amplitude-frequency response curves of vehicle body

从图2可以看出，当悬挂系统存在阻尼时，二阶模态频率ω2=6.39 rad/s对应的车体振幅峰值基本消失，只有一阶模态频率ω1=2.24 rad/s对应的车体振幅最大，振动最恶劣，振幅最大值可达0.19 m。

下面考虑在外激励频率趋近系统一阶振动模态频率时线性时滞反馈控制的减振特性，得到的车体振幅随反馈增益系数和时滞变化如图3所示。

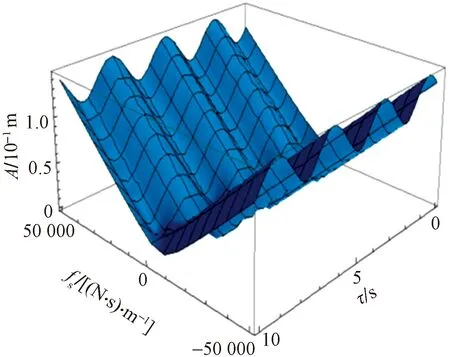
图3 反馈增益系数和时滞对车体振幅的影响Fig.3 Effects of gain and time delay on amplitude of vehicle body

由图3可以看出，车体振幅A受到反馈增益系数和时滞两个控制参数的影响，对于某一特定的时滞参数，反馈增益系数fs=-7 506.18 (N·s)/m时车体的振幅最小，因此可选定反馈增益系数为fs=-7 506.18 (N·s)/m。反馈增益系数确定之后，可以在某些时滞区间选择时滞参数达到抑制车体振幅的目的，但同时要对系统进行稳定性分析，保证系统在稳定的状态下工作，在此对线性时滞反馈控制系统不做详细介绍。下面考虑非线性系统及时滞反馈控制的效果。

3 非线性系统的近似多尺度法

对非线性时滞反馈控制系统，采用多尺度方法结合模态设解的方法进行分析。首先，将式(1)、式(2)写成矩阵的形式为

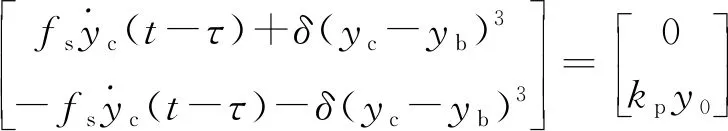
(3)

将式(3)的解设为模态解的形式yc=q1+q2，yb=r1q1+r2q2，即：

(4)

式(4)为(yc,yb)与(q1,q2)两组坐标之间的变换关系，其中坐标变换矩阵设为u，其转置为uT。

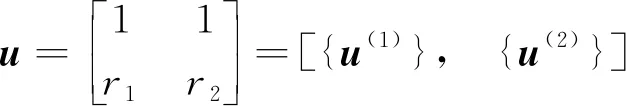
(5)

将式(4)代入式(3)，再将式(3)左乘矩阵uT得：

(6)

(7)

为方便采用多尺度方法进行摄动分析，将各量标注如下：mc=m1，mb=m2，ks=k1，kp=k2，cs=εc1，cp=εc2，δ=εδ，fs=εfs，fs=εfs。则式(7)可写为

δ(1-r1)(q1+q2-r1q1-r2q2)3]

(8)

εr2k2fcos(Ωt)-ε[c1-r1c1-r2c1+

δ(1-r2)(q1+q2-r1q1-r2q2)3]

(9)

采用多尺度法对系统动力学方程进行摄动分析，求解式(8)、式(9)的二阶近似解，将解的形式表示为

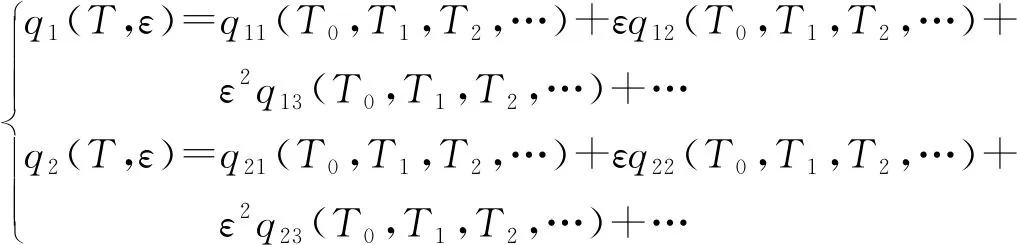
(10)

式(10)中：时间尺度Tr为新引入的自变量，Tr=εrt，r=0,1,2,…，偏导算子为

(11)

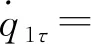
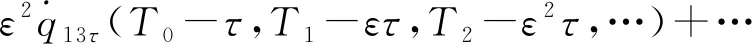
(12)

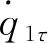
(13)

(14)

将式(10)～式(14)代入到式(8)、式(9)中，并比较ε同次幂，得到：

ε0:

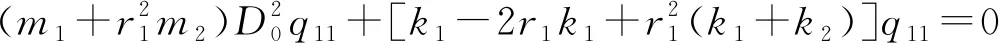
(15)

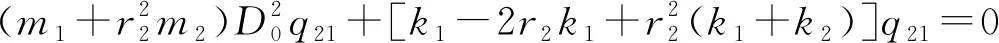
(16)

ε1:

r1r2(c1+c2)]D0q21-[(1-r1)fs(D0q11τ+

D0q21τ)+δ(1-r1)(q11+q21-r1q11-

r2q21)3]+r1k2fcos(Ωt)

(17)

[c1-2r2c1+r1r2(c1+c2)]D0q21-

[(1-r2)fs(D0q11τ+D0q21τ)+δ(1-r2)

(q11+q21-r1q11-r2q21)3]+r2k2fcos(Ωt)

(18)

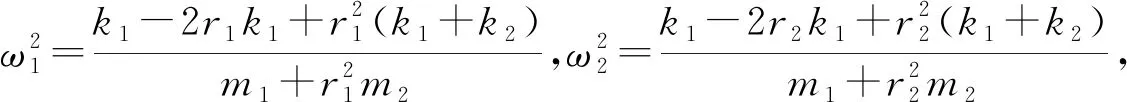
ε0:

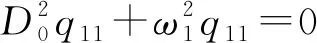
(19)

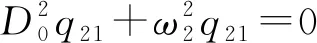
(20)

ε1:

[c1-r1c1-r2c1+r1r2(c1+c2)]D0q21-

[(1-r1)fs(D0q11τ+D0q21τ)+δ(1-r1)×

(q11+q21-r1q11-r2q21)3]+r1k2fcos(Ωt)}

(21)

[c1-2r2c1+r1r2(c1+c2)]D0q21-

[(1-r2)fs(D0q11τ+D0q21τ)+δ(1-r2)×

(q11+q21-r1q11-r2q21)3]+r2k2fcos(Ωt)}

(22)

设微分方程组的解为

q11=A(T1)eiω1T0+cc

q21=B(T1)eiω2T0+cc

(23)

式中:A和B是未知的函数；cc代表其前面各项的共轭。外激励项和时滞项可以表示为

(24)

(25)

将式(24)、式(25)代入到式(21)、式(22)中得：

K3e3iω1T0+K4e3iω2T0+K5eiT0(-2ω1+ω2)+

K6eiT0(2ω1+ω2)+K7eiT0(-ω1+2ω2)+

K8eiT0(ω1+2ω2)+K9eiω1(T0-τ)+

K10eiω2(T0-τ)+K11eiΩT0]+cc

(26)

K14e3iω1T0+K15e3iω2T0+K16eiT0(-2ω1+ω2)+

K17eiT0(2ω1+ω2)+K18eiT0(-ω1+2ω2)+

K19eiT0(ω1+2ω2)+K20eiω1(T0-τ)+

K21eiω2(T0-τ)+K22eiΩT0]+cc

(27)

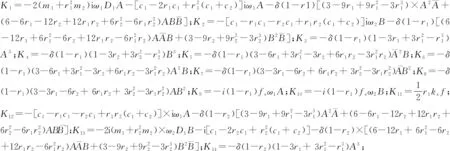
4 非线性系统平衡解线性系统的幅频及减振特性

由系统幅频曲线可以看出，车体的一阶模态振幅最大。下面研究外激励频率趋近系统的一阶模态频率时振动系统的平衡解。为此，引进及分别表示外主共振解谐参数和1∶3内共振解谐参数为

(28)

式(26)、式(27)可写成如下形式：

K3e3iω1T0+K4e3i(3ω1+εσ2)T0+

K5eiT0(ω1+εσ2)+K6eiT0(5ω1+εσ2)+

K7eiT0(5ω1+2εσ2)+K8eiT0(7ω1+2εσ2)+

K9eiω1(T0-τ)+K10ei(3ω1+εσ2)(T0-τ)+

K11ei(ω1+εσ1)T0}+cc

(29)

K14ei(ω2-εσ2)T0+K15e3iω2T0+

(30)

得到式(29)、式(30)的可解性条件，并化简得到：

(31)

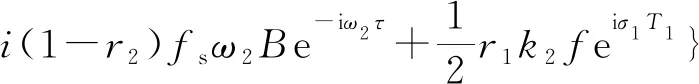
(32)

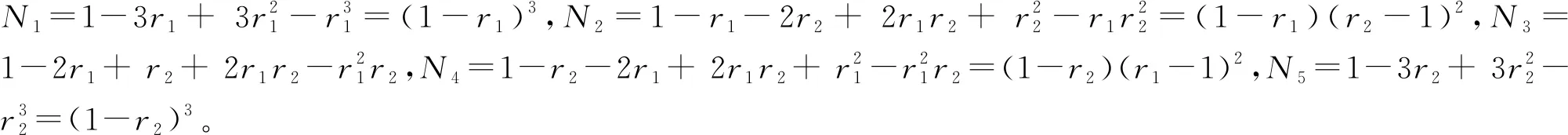
(33)

(34)

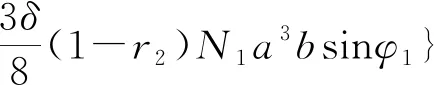
(35)

(36)

式中：φ1=θ2-3θ1+σ2T1，φ2=σ1T1-θ1。

为了确定对应的稳态运动的定常解振幅和相位，即在a′=b′=φ′1=φ′1-3φ′2=0时的平衡解，以判断平衡解的稳定性，首先将式(33)～式(36)转化到直角坐标系下：为此，设：s1=acosφ2，d1=asinφ2，s2=bcos(φ1-3φ2)，d2=bsin(φ1-3φ2)，则式(33)～式(36)变为

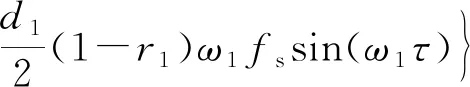
(37)

(38)

s′2=b′cos(φ1-3φ2)-b(φ′1-3φ′2)×

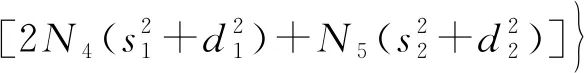
(39)

d′2=b′sin(φ1-3φ2)+b(φ′1-3φ′2)×

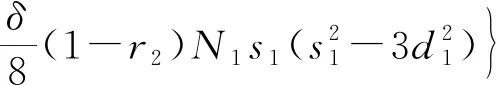
(40)

5 非线性系统的时滞反馈控制

车体的位移形式可以近似表达为

yc=q1+q2=q11+q21+ε(q12+q22)+

ε2(q13+q23)+…≈q11+q21≈

acos[ω1T0+θ1(T1)]+

bcos[ω2T0+θ2(T1)]=y1+y2

(41)

式(41)中：y1=acos[ω1T0+θ1(T1)]，y2=bcos[ω2T0+θ2(T1)]。

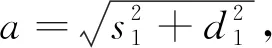
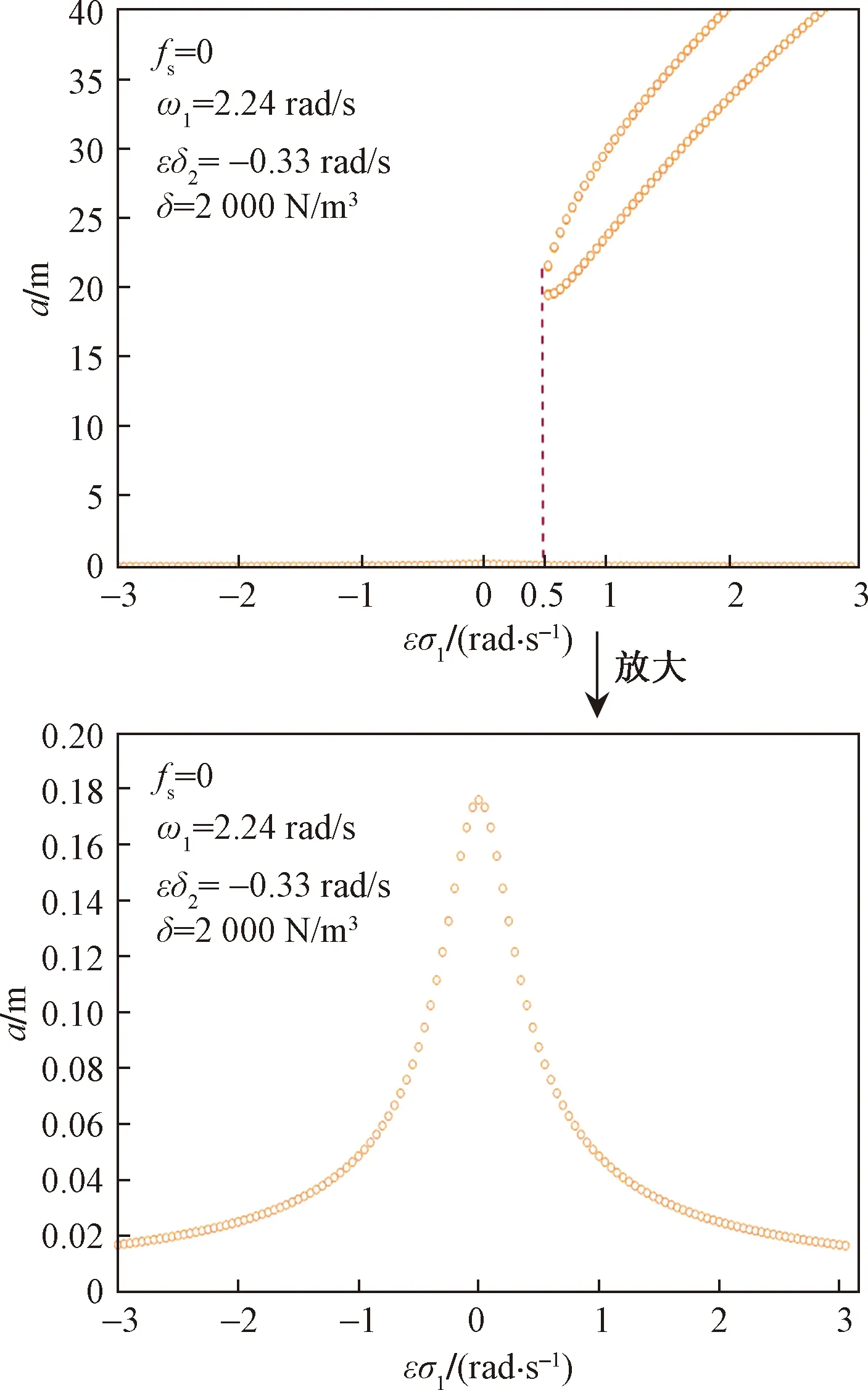
图4 车体的幅频响应曲线aFig.4 Amplitude-frequency response curves a of vehicle body

从图4、图5可以看出，当外激励在主共振点右侧(即εσ1>0.5)，振动系统的幅频响应曲线出现了多解现象，对应某一个确定的外激励频率有三个解支，其中上下两条曲线是稳定的，中间的曲线是不稳定的。根据非线性系统的特性很容易判断，当振动系统的初始条件较小时，系统对应振幅较小的解支；当振动系统的初始条件较大时，系统对应振幅较大的解支。而且容易观察到，振幅a的量级要远远大于振幅b的量级，因此对于主动控制系统，重点讨论采用时滞反馈控制振动系统在主共振点及其附近对振幅a的控制效果。以外激励频率分别在εσ1=-0.2 rad/s、εσ1=0和εσ1=0.2 rad/s三点为例进行研究。图6是时滞系统的车体振幅随时滞量的变化曲线，根据以上分析，反馈增益系数选择为fs=-7 506.18 (N·s)/m。

从图6可以看出，振幅a随着时滞量的变化呈现周期性的变化趋势，有波峰和波谷，这说明时滞对振动系统的振幅有调节作用。理论上存在某些时滞区间，在这些区间内振动系统的振幅有明显的减小，可以在这些时滞的减振区间内调节时滞量，以达到抑制车体振幅的目的。然而在某些时滞区间内，由于时滞量的出现导致了系统出现不稳定，系统的振动将更加恶劣，在实际工作中应避免将时滞调节到不稳定区间内。

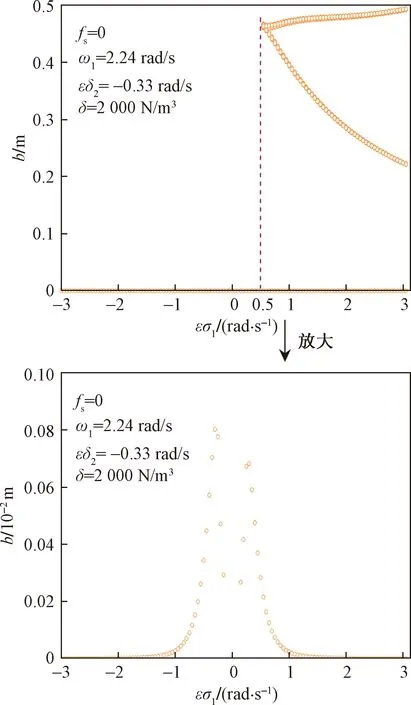
图5 车体的幅频响应曲线bFig.5 Amplitude-frequency response curves b of vehicle body

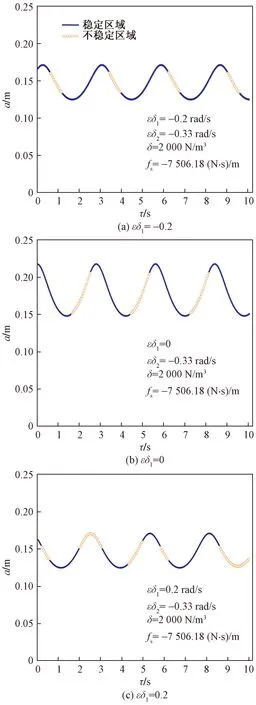
图6 车体的振幅-时滞响应曲线Fig.6 Amplitude-delay response curves of vehicle body

6 数值模拟

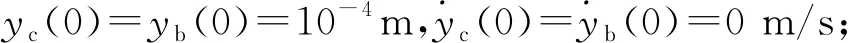
图7 车体时间历程响应曲线Fig.7 Time history response curves of vehicle body

从图7中车体位移的时间历程响应曲线可以看出，图7(a)为被动系统，振幅约为0.19 m。图7(b)为采用时滞反馈控制，且时滞量为零时的情况，可以看出系统的振幅增大了，振幅约为0.24 m，说明采用无时滞的反馈控制系统的振幅反而增大了。图7(c)为在时滞减振区间内的选择的时滞量，当时滞量选择为τ=0.8 s时，振幅减小了，约为0.17 m，说明时滞反馈有抑制系统振幅的作用。图7(d)为在时滞减振区间内的选择的一个最佳时滞量，当时滞量选择为τ=1.35 s时，振幅减小到最小值，约为0.16 m，说明时滞量的合理选择能够达到最好的减振状态。实际上时滞量的最佳减振点不是唯一的，当选择为τ=4.16 s也能到达最佳减振效果。

7 结论

对两自由度高速列车半主动悬挂系统的垂向振动进行研究，考虑了二系悬挂中的刚度三次非线性。通过利用设模态解、方程解耦、多尺度等方法对振动方程进行求解，得到了系统的二次近似解析解，分析了系统在主外共振和1∶3内共振同时存在时的动力学行为。采用时滞反馈控制系统的振动，分别对线性和非线性时滞减振性能进行了分析，得到的主要结论如下：

(1)所用到的物理参数都是有实际量纲的参数，在此基础上对悬挂系统进行的分析和计算都是有实际物理意义的，对工程实际有重要参考价值。

(2)对线性被动控制系统，得到了振动系统的幅频响应曲线，由于二阶模态的振幅远远低于一阶模态的振幅，重点研究了当外激励频率趋近一阶模态频率和1∶3内共振的同时存在时采用时滞反馈控制系统的振动。

(3)对线性时滞反馈控制系统，得到了车体振幅相对反馈增益系数和时滞变化的图形，找到了最佳的反馈增益系数。针对所有的时滞，当反馈增益系数取得该值时车体的振幅最小。

(4)对非线性时滞反馈控制系统，得到了车体振幅随着时滞量变化的响应曲线，得到了时滞的减振区间，在该区间内选择时滞量能够达到抑制车体振幅的目的。并且存在一些时滞的最佳值，当时滞选择该数值时车体的振动能够抑制到最小。

(5)时滞是可以利用的控制参数，合理地利用时滞能够达到抑制系统振动的目的；同时时滞也是导致系统不稳定的因素，在某些时滞区间能够导致系统失去稳定导致破坏。

(6)数值模拟结果和解析结果吻合，证明了结果的正确性和可靠性。