分类讨论思想在中考解题中的应用

张成艳 韦宏

摘 要：分类讨论的题型是中考数学中重要考查的题型之一，文章以南宁市中考题为例，讨论分类讨论思想在中考解题中的应用，以此进一步强调分类讨论思想在初中数学学习中具有重要的作用，希望学生在学习的过程中能够重视分类讨论思想的学习。

关键词：分类讨论思想;中考;解题;应用

分类讨论思想是一种重要的逻辑方法之一，它可以加强学习者对数学的学习。九年义务教育2011年初中数学课程标准提到：“数学思想蕴含在数学知识的形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象和概括。”因此，教师要不断地向学生渗透数学思想方法，丰富学生的数学思想方法的学习。

一、 应用分类讨论思想解决初中数学题的重要性

所谓的分类，是把一个“属概念”分为若干个“种概念”的逻辑划分方法。分类讨论是一种重要的逻辑方法，在初中数学的教学过程中，教师只有重视培养学生分类讨论的思想，才可以进一步的提高学生的逻辑推理能力，加深学生对相关数学知识点的理解和掌握。下面将选取几道南宁市中考考查到分类讨论思想的题型进行分析，进一步强调应用分类讨论思想对解决初中数学题的重要性。

二、 分类讨论思想在中考解题中的应用

（一）分类讨论思想在一次函数中的应用

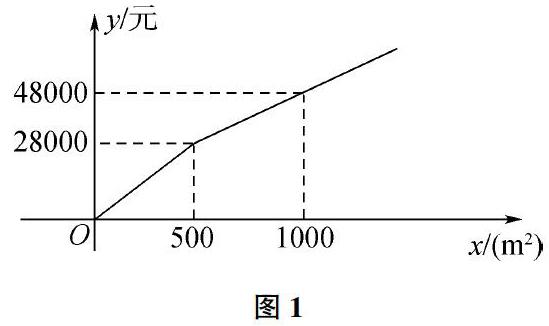
例1 （2009年）甲、乙两个工程队参加狮山公园的竞标，甲队铺设砖的造价

y甲（元）与铺设面积x（m2）的函数关系如下图所示;

y乙=kx是乙队铺设砖的造价y乙（元）与铺设面积x（m2）的函数关系式

（1）结合下图，求出甲队铺设砖的造价与铺设面积的函数关系式

（2）若铺设砖的面积为1600m2，选择哪个工程队进行施工费用最划算

分析：（1）由图1可知甲工程队造价与面积的关系是一个分段函数，运用分类讨论的思想，可以把此函数分为两段进行求解：①当时，设y甲=k1x，把（500，28000）代入y甲=k1x，就可以求出造价与面积地关系;

②当时，设y甲=k2x+b，把（500，28000）、（1000，48000）代入y甲=kx+b，就可以得到造价与面积的关系。要考虑两种情况求出的关系式，遗漏任何一种情况，都会导致学生被扣分;第（2）题当x=1600，可以求解出甲工程队的造价，但是乙

工程队的造价无法进行求解，所以，此时需要运用分类讨论思想去考虑乙工程队的造价范围。可以分为三种情况进行讨论：

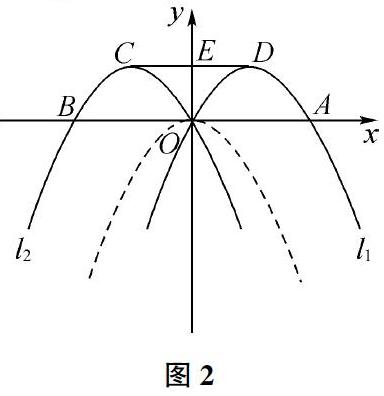
第①种情况：当y甲=y乙时;第二种情况②当y甲>y乙时;第三种情况③当y甲

点评：解（1）要懂得判断该函数是一个分段函数，要懂得运用分类讨论的思想去讨论在不同的铺设范围内，甲工程队施工的造价与面积的函数关系式是不一样的。如果在解决本题中学生不懂得运用分类讨论的思想去求解造价与面积的函数关系式，那么学生无论是在取哪个铺设面积的取值范围，去求解甲工程队造价与面积的关系式都是不全面的。学生只有掌握分类讨论的思想，在解决问题时才能思考全面。解（2）要懂得根据甲工程队的造价，运用分类讨论的思想去讨论乙工程队施工的造价范围。只有分类的讨论乙工程队的造价范围，才能知道哪个工程队的价格划算。

2009年南宁市中考是在第24题考查了学生分类讨论的思想，本题结合了分段函数对学生进行考查。运用分类讨论思想是解决本题的关键。学生只有掌握分类讨论的思想，在解本题时才能够思考全面。分类讨论思想是中考数学中常考的一种思想，学生只有充分地掌握它，在中考解题的过程中才会思考全面，不会遗漏任何一种方法而导致在中考中丢分。因此，教师要注重培养学生的数学思想。如果教师不断地向学生渗透数学思想，那么学生就能充分地掌握相关的数学思想方法。

（二）分类讨论思想在二次函数解题中的应用

例2 （2010年）如图2，把抛物线y=-x2（虚线部分）先向右平移1个单位，再向上平移1个单位得到抛物线l1，抛物线l2与抛物线l1关于y轴对称。抛物线l1与x轴的交点为A点，抛物线l2与x轴的交点为B点，点O为坐标原点。抛物线l1的顶点是D点，抛物线l2的顶点是C点，线段CD交y轴于点E。

（1）设点P是抛物线l1上的任意一点（但不与D、O两点重合），P点关于y轴对称的点为Q点，请你判断四边形PQCD是什么特殊的图形？并且说明你的理由。

（2）是否存在点M在抛物线l1上，使得S△ABM=S四边形AOED，如果存在，请你求出点M的坐标，如果不存在，请你说明理由。

分析：（1）有两种可能。①当P点是l2的对称轴与l1的交点时，求解的四边形CPQD为矩形;

②当点P不是l2的对称轴与l1的交点时，求解得到四边形CPQD（或者四边形CQPD）是等腰梯形。（2）根据抛物线的解析式，可以求出点A，点B，点E的坐标分别为：A（2，0），B（-2，0），E（0，1），可以得到梯形AOED的面積，由图形可知AB是定长，由三角形ABM的面积，可以求解出点M的纵坐标的绝对值，此时需要分类讨论求解点M的纵坐标：①当y>0时，②当y<0时，最后再将点M的纵坐标代入抛物线的解析式中，可以求解出点M的坐标点。

点评：本大题结合二次函数和动点等知识考查了分类讨论思想，是中考压轴题，这类题型学生很难拿满分。解决本题的关键在于学生是否能够熟练地运用分类讨论思想。分类讨论思想是中考重点考查的思想方法之一，学生要想在中考中胜出，在遇到这种题型时，就必须会运用分类讨论思想去讨论每一个情况，学生只有掌握分类讨论思想，遇到这类题型才能够全面地去分析。（1）只有分类的去讨论点P的情况，才能够全面地考虑到四边形CPQD是什么特殊的四边形。（2）要懂得判断根据的面积只是求解出点M的纵坐标的绝对值，需要运用分类讨论的思想去求解点M的纵坐标，学生只有熟练地掌握分类讨论的思想，在解决本小题时，才能够全面地考虑到点M的坐标有多种情况。如果学生没有掌握分类讨论的思想方法，那么求解点M的坐标时，学生往往会漏掉某一种情况，导致在中考中丢分。因此，在初中数学教学中，教师要注重培养学生的数学思想，加强学生解决数学问题的能力。

（三）分类讨论思想在实际问题中的应用

例3 （2014年）某公交公司计划购买A型和B型两种环保节能的公交车一共10辆。购买1辆A型车和2辆B型车，一共需要400万元;购买2辆A型车和1辆B型车，一共需要350万元。

（1）在该线路上A型车每辆年均载客的量是60万人次，B型车每辆年均载客的量是100万人次。如果该公司购买A型和B型车的总费用不超过1200万元，且确保这10辆车在该线路的年均载客量总和不低于680万人次，那么该公司的购车方案有哪几种？哪种购车方案的总费用最便宜？最便宜的总费用是多少？

分析：根据题目的已知条件（购买A型和B型车的总费用不超过1200万元，且这10辆车的年均载客量总和不低于680万人次）可以列出一元一次不等式组，从而求解出A型公交车数学的取值范围，然后运用分类讨论的思想方法去讨论购买的方案。

求解本小题运用到了分类讨论的思想。在求解出A型公交车的购买范围后，可以分三种情况去讨论该公交车公司的购买方案。如果学生掌握了分类讨论思想，并且能够熟练地运用分类讨论思想解题，那么学生在解决本题时就会全面地考虑所有的方案，不会遗漏某种购买方案，从而可能导致求出的结果并不是最佳购买方案，从而导致在中考中丢分。学生只有熟练地掌握分类讨论的思想，在解决本小题时，才能够充分地考虑所有的购买方案。因此，掌握分类讨论思想至关重要。教师在教学中要注重数学思想的渗透，注重加强学生运用分类讨论思想去解决问题的训练。

综上所述，分类讨论思想是中考数学考查的一种重要思想，在中考数学解题中广泛的应用。文章只是列举2009年，2010年，2014年这三年中的其中一道简答题。从上述的分析可以看出，分类讨论思想对学生解决中考数学题具有重要的作用。学生只有掌握分类讨论思想，在遇到这类题型时，学生才能够很好地去解决问题;才能够全面地运用分类讨论的思想全面的去考虑每一种情况。分类讨论思想是一种常考查的思想方法，在中考解题中广泛的应用。因此，学生在日常的学习中，要重视分类讨论思想的学习。

参考文献：

[1]中华人民共和国教育部.义务教课程标准[S].北京：北京师范大学出版社，2011.

[2]肖学平.中学数学的基本思想和方法[M].科学出版社，1994.

[3]赵伟.思维定式与中学数学教学的理性思考[J].中学数学杂志，2007（5）.

[4]项楷尧，郑战铭.试用数学思想方法讨论研究逻辑问题：中学数学教学中若干有争议的逻辑问题辨析[J].中学数学，2008（13）.

[5]刘振宇.高等代数蕴含的哲学思想[J].枣庄学院学报，2010（2）.

[6]焦延顺.高中物理学习中常见思维障碍及矫正[J].知识经济，2010（17）.

[7]孔庆兰.《高等代数》中的建构主义思想方法[J].枣庄学院学报，2010（5）.

作者简介：张成艳，海南省海口市，南寧师范大学数学与统计学院;

韦宏，海南省海口市，南宁师范大学数学与统计学院。