M-矩阵Hadamard积的特征值新界

陈付彬

(昆明理工大学津桥学院 理工学院，云南 昆明 650106)

由于M-矩阵在诸多领域的应用价值比较广泛，所以成为现今矩阵理论研究的重要内容，其中，特征值的相关下界和判别法等比较受到学者的青睐。Hadamard积是特殊的矩阵运算[1-2]，至今得到了一些比较好的关于非奇异M-矩阵Hadamard积的特征值下界的结论[3-12]。

针对这一问题，文章做了进一步的探讨，主要是在前人的基础上通过构造迭代公式，利用圆盘定理给出新的结果，使新结果在迭代若干次后更加接近真值，文中也给出了相应的理论证明以及算例，从而验证新结果的有效性。

1 符号与引理

n阶所有实(复)矩阵组成的集合以Rn×n(Cn×n)表示。为证明和叙述方便，给出如下记号：

令A=(aij)∈Rn×n，记N={1,2,…,n}，i,j,k∈N，j≠i。

若A∈Zn={A=(aij)∈Rn×n|aij≤0;i,j∈N,i≠j}可表为A=αI-P，P≥0,α>ρ(P)，称A为非奇异M-矩阵，用Mn表示；若α=ρ(P)，称A为奇异M-矩阵。τ(A)=min{Re(λ):λ∈σ(A)}表示A的最小特征值。

A°B表示A和B的对应元素相乘，即A°B=(aijbij)，称为A和B的Hadamard积。

2007年，LI等[4]得到一个改进结论：

(1)

2009年，LI等[5]改进式(1)得到下面结论：

(2)

2013年，LI等[7]又给出下面结论：

(3)

2014年,高美平[8]改进式(2)式得到：

(4)

2015年，蒋建新等[9]改进式(1)(2)(4)，给出如下结论：

(5)

2016年，刘新[10]又对式(1)进行了改进，得到如下结论：

(6)

针对该问题，文章将做深入的探讨，给出改进以上结果的新估计式。

2 主要结果

引理1[3]设A,B∈Mn，则A°B-1∈Mn。

引理2[13]设A=(aij)∈Rn×n是行严格对角优势矩阵，则A-1=(bij)满足

引理3[1]若A是M-矩阵，则有正对角矩阵D使D-1AD为行严格对角优势的M-矩阵。

引理4[14]设A,B∈Rn×n，则有对角矩阵E,F,使下式成立：

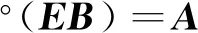
引理5[13]若A-1是双随机矩阵，则Ae=e，ATe=e，其中e=[1,1,…,1]T。

引理6[15]设A=(aij)∈Cn×n，x1,x2,…,xn>0，则A的特征值包含在如下范围：

定理1设A=(aij)∈Rn×n是行严格对角优势的M-矩阵，则A-1=(βij)满足

证明由ri,mji,hi,wji,ti的定义及A是行严格对角优势矩阵，可知0≤wji≤mji≤ri<1，0≤hi≤1, 0≤ti≤1,j≠i,i∈N。

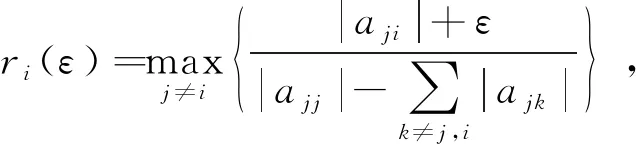
因A是行严格对角优势矩阵, 则一定存在ε>0, 能够使下式成立：

0

令Wi(ε)=diag(w1i(ε)ti(ε),…,wi-1,i(ε)ti(ε),

1,wi+1,i(ε)ti(ε),…,wni(ε)ti(ε))，i∈N。

当j≠i，j,i∈N时, 由ti(ε)的定义，得

所以

(7)

当j=i，j,i∈N时，

(8)

从式(7)和(8)可知,AWi(ε)是行严格对角占优M-矩阵。

由引理2，得

即

令ε→0, 可知

注1由于wjiti≤mjihi≤mji≤ri,j≠i,j,i∈N，因此，定理1分别改进了文献[5]中引理2.2，文献[6]中引理2.2及文献[7]中引理2的结果。

定理2设A∈Mn, 且A-1=(βij)是双随机矩阵，则

证明因为A是M-矩阵, 且A-1=(bij)是双随机矩阵, 则

所以，A是行严格对角占优矩阵。

由定理1，得

即

定理3设A=(aij),B=(bij)∈Mn，且A-1=(βij)，则

证明因A∈Mn, 由引理3和引理4，可设A是严格对角优势M-矩阵。

(1)A,B不可约。对任意i∈N,0

即

因为AA-1=I, 即

(2)A,B至少有一个可约。令M=(mij)是满足m12=m23=…=mn1=1,其余mij均为零的置换矩阵。当ε>0时，A-εD和B-εD是M-矩阵且不可约[16],将A和B替换为A-εD和B-εD，当ε→0时, 结论依旧成立。

由定理2和定理3，可得如下两个推论:

推论1设A=(aij),B=(bij)∈Mn，且A-1=(βij)是双随机矩阵，则

推论2设A=(aij)∈Mn，且A-1=(βij)是双随机矩阵，则

注2因为wjiti≤mjihi, 所以

因此

所以

故推论2改进了文献[7]中的推论2。

3 数值算例

令

依据Fiedler和Markham猜想得τ(A°A-1)≥0.5；依据式(1)得τ(A°A-1)≥0.662 4；依据式(2)得τ(A°A-1)≥0.799 9；依据式(3)得τ(A°A-1)≥0.832 1；依据式(4)得τ(A°A-1)≥0.825 0；依据式(5)得τ(A°A-1)≥0.825 1；依据式(6)得τ(A°A-1)≥0.762 5；依据本文推论2得τ(A°A-1)≥0.835 8。