基于CEEMD-SSA-ELM的短期电价集成预测模型

张 宁

(闽江学院 物理与电子信息工程学院，福建 福州 350108)

电价能够有效体现电能的供需变化，并可具体反映电力市场运营情况。对电价数据进行精准的预测将有助于售电企业决定市场报价，并能及时地规避市场风险。然而，由于短期电价受到天气、日常活动、商务交易、供给侧报价等多种因素的综合影响，导致其具有典型的非平稳性与非线性的特点。由于很难准确拟定顾及诸多影响因素的数学模型，采用经典的因果关系回归模型进行短期电价预测往往精度较低。近年来，另一种将历史电价作为时间序列进行建模预测的方式得到了广泛的研究。常用的时间序列预测方法有自回归滑动平均模型(autoregressive moving-average model，ARMA模型)[1]，广义自回归条件异方差模型(generalized autoregressive conditional heteroskedasticity model，GARCH模型)[2]等，但这些方法都是基于线性序列进行建模分析，其对于捕捉电价序列中的非线性特征能力有限，这也导致其预测结果的精度并不高。随着人工智能技术的飞速发展，人工神经网络(artificial neural network，ANN)、支持向量机(support vector machine，SVM)等非线性方法在电价预测领域中已取得了较为成功的应用[3-5]。

为了进一步提高电价时间序列预测的精度，目前一种基于“分解-预测-集成”思想的混合预测方法被广泛的关注和研究[6-8]。其预测思路为：首先采用小波变换(wavelet transform，WT)、经验模态分解(empirical mode decomposition，EMD)等信号分解方法将电价序列分解为多个分量，进而对每个分量采用ANN、SVM等非线性方法进行独立预测，最后将所有分量预测进行重构集成。该类方法已经证实可以有效提高预测精度[8]；但是，小波变换需要对小波基函数、分解层数进行预先设置，所以小波变换并不是一种自适应的分解方法，而EMD方法也难以避免模态混叠现象的发生。另外，ANN方法存在有训练速度慢、易陷入局部极小等问题；SVM方法也存在难以合理选择模型参数的缺点。特别地，对于该类混合预测方法，由于分解后的最高频分量的随机性最强，其独立预测的难度也最大。文献[7]提出将最高频分量舍去后对其余分量进行预测集成，但是这种舍去方式显然也会影响最终的预测精度。

为了有效解决上述问题，本文提出CEEMD-SSA-ELM模型，并以澳大利亚昆士南州和新南威尔士州的电力市场某月的电价数据作为研究对象，进行了电价预测。实验取得了较高的预测精度，也验证了所提方法的有效性。

1 理论背景

1.1 CEEMD的基本原理

由于应用EMD方法对信号分解所获得的固有模态函数(instrinsic mode function，IMF)会存在模态混叠问题，WU等[9]基于辅助白噪声分析提出了一种集成经验模态分解(ensemble empirical mode decomposition，EEMD)方法以避免该现象的发生，但是，EEMD方法也存在有难以消除重构信号中的残余辅助白噪声的缺陷。YEH等[10]在EEMD的基础上，以采用正、负成对的形式加入辅助白噪声，提出了CEEMD方法。该方法的计算效率较高，并可在重构信号时完全消除残余辅助噪声，其计算流程为：

(1)向原始信号S中加入N组正、负成对的辅助白噪声X，得到

(1)

式中：M1为添加正噪声后的信号；M2为添加负噪声后的信号。由式(1)可以得到2N个集成信号。

(2)对每个信号使用EMD进行分解，将第i个信号的第j个IMF分量记为IMFij。

(3)对每个信号分解后的对应分量取均值以得到最终分解结果为

(2)

1.2 SSA的基本原理

SSA是一种可以对信号进行趋势或准周期成分的降噪与提取的方法。其具体处理步骤为[11-13]：

(1)将一维时间序列[X1,X2,…,XN]映射为L×K轨迹矩阵

(3)

式中： 2≤L≤N；K=N-L+1。

(2)对XXT进行奇异值分解，得到L个降序排列的非负特征值λ1≥λ2≥…≥λL≥0,以及对应的特征向量U1,U2,…,UL，则矩阵X为

X=X1+X2+…+Xd。

(4)

(3)分组：将集合{1,2,…,d}分割成p个不相交的子集I1,I2,…,Ip，则式(4)为

X=XI1+XI2+…+XIp。

(5)

X=XI1+XI2。

(6)

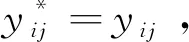
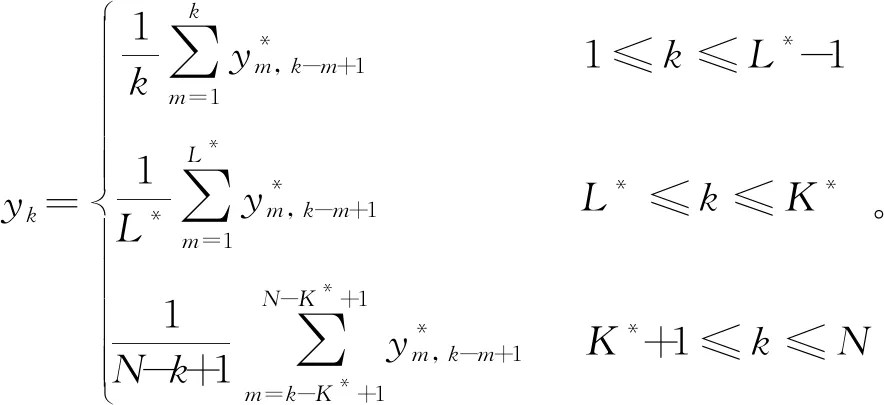
(7)

本文对矩阵XI1应用式(7)重建时间序列，以实现将噪声从原始序列中分离。

1.3 ELM的基本原理

ELM是HUANG等在2006年提出的一种进化神经网络方法[14]，可以避免传统ANN方法存在的训练速度慢、易陷入局部极小等缺陷。ELM数学模型为

Hβ=Y。

(8)

式中：H为隐含层的输出矩阵;Y为目标输出矩阵;β为连接隐层神经元和输出节点的权值矩阵。

ELM的训练目标是寻找最优权值W=(w,b,β)，以使下式成立：

minE(W)=min‖Hβ-Y‖，

(9)

其中，隐含层节点的输入权值w和偏置b被随机赋值。此时，ELM的训练过程即为求解式(8)的线性方程组，其最小二乘解为

β=H+Y。

(10)

式中：H+为隐层输出矩阵H的Moore-Penrose广义逆，则ELM网络输出

F=Hβ。

(11)

2 短期电价预测的CEEMD-SSA-ELM方法

2.1 基于CEEMD的短期电价序列分解

对电价序列{X(t),t=1,2,…,N}采用CEEMD方法进行自适应分解，可以分解出j个IMF分量和1个残余分量R，则X(t)为

(12)

2.2 基于SSA的最高频分量趋势提取

由于第1个最高频分量IMF1变化剧烈、随机性强，直接建模预测的效果较差，且将会影响整体的预测精度，因此，利用SSA对其去噪处理并提取趋势项，记为IMF1′。

2.3 基于ELM预测模型结构的确定

对于短期电价序列，假定t时刻的电价X(t)可以由(t-1,t-2,…,t-m)时刻的历史电价X(t-1),X(t-2),…,X(t-m)来进行预测，则预测模型为

X(t)=f[X(t-1),X(t-2),…,X(t-m)]。

(13)

式中：f(·)为映射函数；m为嵌入维数。原始电价序列在经过CEEMD-SSA处理后，其第1个最高频分量预测模型根据式(13)可变为

IMF1′(t)=f[IMF1′(t-1),IMF1′(t-2),…,IMF1′(t-m)]，

(14)

其余j-1个IMF分量的预测模型为

IMFi(t)=f[IMFi(t-1),IMFi(t-2),…,

IMFi(t-m)]，

(15)

残余分量的预测模型为

R(t)=f[R(t-1),R(t-2),…,R(t-m)]。

(16)

2.4 CEEMD-SSA-ELM方法流程图

综上，将CEEMD-SSA-ELM应用于某地区电价预测中，可得到CEEMD-SSA-ELM模型的流程图，如图1所示。

2.5 预测模型的评价指标

为了定量评价电价预测模型的精度，本文选取2种评价指标：

图1 CEEMD-SSA-ELM预测模型流程Fig.1 Structure of CEEMD-SSA-ELM prediction model

(1)均方根误差

(2)平均绝对百分误差

3 实例分析

3.1 实例1

本文以澳大利亚昆士兰州2016年6月1日00：30：00至2016年7月1日00：00：00共30 d的电价数据为研究对象，每半小时采集一次，共计1 440个短期电价时间序列。澳大利亚昆士兰州原始电价数据序列如图2所示。

为了减少数据量纲对建模的影响，采用下式将原始电价序列数据归一到[-1,1]区间：

X′(t)=2(X(t)-Xmin)/(Xmax-Xmin)-1。

(17)

式中：X′(t)为归一化后的电价序列；Xmin、Xmax分别为原序列中的最小值、最大值。在建模计算结束后，对输出的训练与预测数据进行反归一化处理，可将其还原至原始区间。

对归一化处理后的电价序列{X′(t),t=1,2,…,n}应用CEEMD方法进行自适应分解，其中，集成次数N=100，噪声标准差设为0.2。分解后可得到10个IMF分量以及1个残余分量。

图2 澳大利亚昆士兰州原始电价数据序列 (0.5 h)Fig.2 The original electricity price series of Queensland, Australia (0.5 h)

对IMF1使用SSA方法进行去噪处理。在此过程中需确定其窗口长度L和重构选取的特征值个数k。文献[12]建议L不大于N/2，且如果原序列总存在整数周期的分量，L应取与该周期成正比的数值。在本例中，采样周期为1 d(48个采样点)，故经测试后设置L=12。图3给出了最高频分量IMF1的奇异谱图。

图3 最高频分量IMF1的奇异谱图Fig.3 Singular spectrum of maximum frequency component IMF1

从图3可以看出：将SSA方法中的矩阵XXT特征值由大到小排列，自第7个特征值开始，下降速率增大，且前7个的贡献率为81.7%；根据设置的贡献率阈值(80%)，即可将k选为7。图4给出了经SSA处理前后的最高频分量，其中，红色虚线即为提取的趋势项。

图4 SSA处理前后的最高频分量Fig.4 Maximum frequency component before and after SSA Processing

对经CEEMD-SSA处理后的第一分量和其余分量序列设置嵌入维数，构建样本数据集。本文嵌入维数都设置为8，即由前8个数据预测第9个数据。由此，总样本数目可构建为1 432个，统一以最后240个电价为预测对象，则训练样本数目设置为1 192个。在此基础上，对每个分量序列分别建立ELM模型，其中，隐层神经元节点数均设置为14，激活函数均选择为“Sig”函数。由于ELM采用了随机权值和偏置的获取方式，将会使模型预测单次结果出现不稳定现象。为此，在进行预测时，各循环操作了100次，并取其预测均值作为最终预测结果。

为了与本文方法进行对比，还建立了另外2种预测模型：(1)不使用SSA处理最高频分量的CEEMD-ELM模型；(2)直接对电价数据进行预测的ELM模型。为了对比的公平性，这2种模型的参数均与本文所提模型设置完全一致。各种模型的预测结果如图5所示。

从图5可以看出：CEEMD-SSA-ELM模型的预测结果曲线与真实电价曲线的吻合度较高，充分表明了该模型具有良好的预测精度；CEEMD-ELM模型和ELM模型的预测曲线明显偏离真值。3种模型精度指标统计结果见表1。

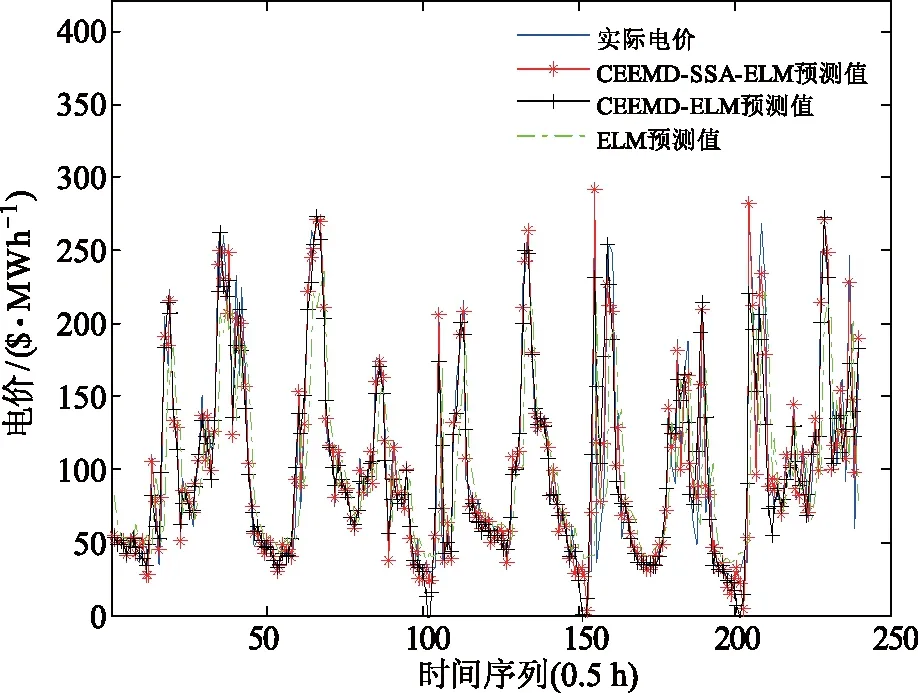
图5 澳大利亚昆士兰州实际电价与预测电价对比Fig.5 Comparison betweenpractical price and predicted price of Queensland, Australia

表1 3种模型预测精度指标对比Tab.1 Comparison of three models for forecasting precision index

从表1可以发现：CEEMD-SSA-ELM模型的预测精度最优，ELM模型预测性能最差；与CEEMD-ELM模型相比，CEEMD-SSA-ELM模型仅增加使用SSA对最高频分量处理并提取趋势项进行预测，但是，均方根误差与平均绝对百分误差分别减少了46.3%和44.8%，说明了SSA处理的必要性和有效性。

3.2 实例2

为了进一步验证本文方法的有效性，第2个实例是以澳大利亚新南威尔士州在相同的时间段的电价数据为研究对象，即2016年6月1日00：30：00至2016年7月1日00：00：00共30 d，每半小时采集一次，共计1 440个短期电价时间序列。澳大利亚新南威尔士州原始电价数据序列如图6所示。

应用CEEMD方法对上述数据进行自适应分解，对最高频分量进行SSA处理。图7给出了最高频分量IMF1的奇异谱图。从图7可以看出：矩阵XXT的特征值从第8个开始，下降速率明显增大，且前8个的贡献率已超过80%，因此将k选为8。

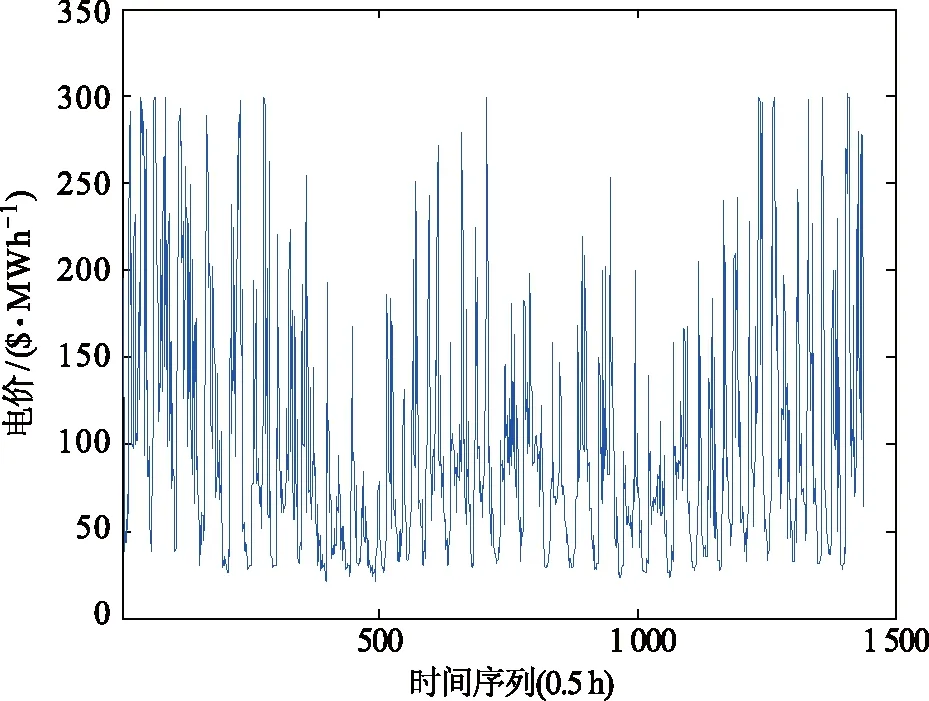
图6 澳大利亚新南威尔士州原始电价数据序列Fig.6 The original electricity price series of New South Wales, Australia

图7 最高频分量IMF1的奇异谱图Fig.7 Singular spectrum of maximum frequency component IMF1

在本例中，各种预测模型的数据集构造、参数设置与实例1完全一致。3种模型的预测结果如图8所示。从图8可以看出：CEEMD-SSA-ELM模型的预测结果曲线与真实电价曲线的吻合度较高，CEEMD-ELM模型和ELM模型的预测曲线明显偏离真值。这与实例1的预测分析结果完全一致。精度指标统计结果见表2。

从表2可以看出： CEEMD-SSA-ELM模型的预测精度最高，CEEMD-ELM模型的预测精度次之，而ELM模型的预测精度最低。这与实例1的预测分析结果完全一致。

图8 澳大利亚新南威尔士州实际电价 与预测电价对比Fig.8 Comparison between practical price and predicted price of New South Wales, Australia

表2 3种模型预测精度指标对比Tab.2 Comparison of three models forforecasting precision index

4 结论

(1)本文提出将一种CEEMD-SSA-ELM模型应用于短期电价序列预测中，取得了较高的预测精度，2个实例的分析结果充分表明该模型在短期电价预测中应用的可行性。

(2)与不加入SSA处理的CEEMD-ELM模型相对比，本文所提模型的均方根误差与平均绝对百分误差分别减少了40%与30%以上，充分说明了SSA对最高频分量处理的必要性和有效性。

(3)本文对各分量建模采用ELM方法，而其输入权值和偏置为随机给定，并非最优。为此，下一步的研究计划是采用优化算法、优化参数以进一步提高预测精度。