(G-V)不变凸多目标规划的最优性条件
江 柳,李向有,刘靖雯
(延安大学 数学与计算机科学学院,陕西 延安 716000)
最优性条件是数学规划中重要的研究内容,自从Hanson在1981年定义了不变凸函数后[1],许多学者推广了不变凸函数,并用来研究不同的规划问题,得到很多重要结论。如文献[2-7]利用不同的不变凸函数研究了多目标规划问题的最优性充分条件和对偶条件。G不变凸函数[8]是不变凸函数的一种推广。ANTCZAK T[9-11]随后用这类函数研究了多目标可微规划问题的最优性条件、对偶性条件和鞍点理论,得到了许多重要结论。KANG Y M[12]和HO J K[13]把G不变凸函数推广到非可微情形,定义了非可微G不变凸函数,并且研究了相应的多目标规划问题。近来,ANTCZAK T[14]进一步把非可微G不变凸函数推广到向量情形,定义了非可微(G-V)不变凸函数,并用这类函数研究了多目标规划问题的最优性条件,得到相关结论。
本文推广了上述G不变凸函数,得出了(G-V)不变拟凸函数、(G-V)不变伪凸函数,并在该推广下得到了其多目标规划的几个最优性充分条件。
1 基本定义
称实值函数f:Rn→R是局部Lipschitz[15]的,若对任意x∈R,存在一个正数k和x的邻域N(x)对任意y,z∈N(x),使得:
‖f(y)-f(z)‖≤k‖y-z‖。
若函数f为局部Lipschitz的,那么函数f:X→R在点x处沿方向d的Clarke广义方向导数和Clarke广义梯度[15]分别定义为:
∂f(x)={ξ∈Rn:f0(x;d)≥ξΤd,∀d∈Rn}。
下面的不等式在全文中成立,对于∀x,y∈Rn,
xy⟺xiyi;x≤y⟺xiyi,但x≠y;
x 设X⊂Rn,u∈X,令f=(f1,…,fk):X→Rk,fi(i=1,…,k)是定义在X上的局部Lipschitz函数,令Ifi(x)(i=1,…,k)表示fi的值, ANTCZAK T在文献[14]中定义了非可微(G-V)不变凸函数,受此启发,我们把非可微(G-V)不变凸函数进一步推广,定义(G-V)不变拟凸函数和(G-V)不变伪凸函数。 考虑下列多目标规划问题(VP): (VP) minf(x)=(f1(x),…,fk(x)), s.t.g(x)≦0, x∈X⊆Rn。 这里,fi:Rn→R(i=1,…,k),g:Rn→Rm,均为局部Lipschitz的实值函数。 (I) ∃λ=(λ1,λ2,…,λk)>0,μ=(μ1,μ2,…,μm)≧0,使得定理1的(a)(b)成立; 由Gfi:Ifi(x)→R,i=1,…,k是严格单调递增实值函数,得: 所以∃λ=(λ1,λ2,…,λk)>0,使得: (1) (2) 由(1)式和(2)式相加,可得: (I)∃λ=(λ1,λ2,…,λk)>0,μ=(μ1,μ2,…,μm)≧0,使得定理1的(a)(b)成立; 由Gfi:Ifi(x)→R,i=1,…,k是严格单调递增实值函数,得: 所以∃λ=(λ1,λ2,…,λk)>0,使得: (3) (4) 由(3)式和(4)式可得: (5) 要使(5)式成立,必有某个j∈{1,…,m},使得: (I) ∃λ=(λ1,λ2,…,λk)>0,μ=(μ1,μ2,…,μm)≧0,使得定理1的(a)(b)成立。 由Gfi:Ifi(x)→R,i=1,…,k是严格单调递增实值函数,得: 则∃λ=(λ1,λ2,…,λk),使得: (6) 由x∈D及定理1中条件(b),得: (7) (6)式与(7)式相加,得: 可得: 本文在G不变凸函数文献的基础上,定义了(G-V)不变拟凸函数、(G-V)不变伪凸函数,并用这类函数研究多目标规划的最优性条件,得到了几个最优性充分条件。由于篇幅问题,本文只是研究了涉及此类函数的最优性条件,后续还可以利用这类新定义函数,研究多目标规划问题的对偶性问题、鞍点问题,还可以给出此类函数的实例并讨论与其他G不变凸函数的关系。
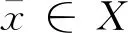
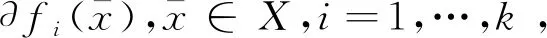
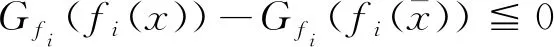
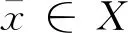

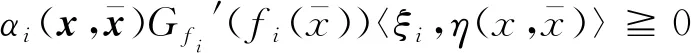
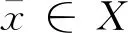
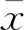
2 最优性条件
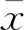
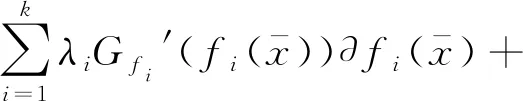

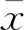
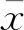
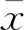
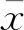


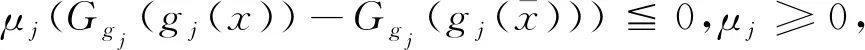
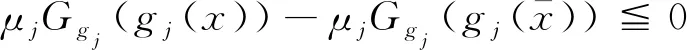
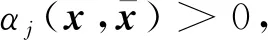
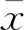
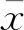
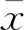
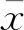


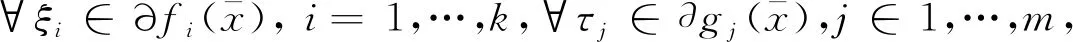


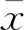
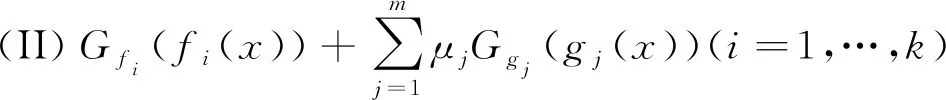
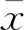


3 小结

