例析“基本条件”相同试题中韦达定理应用的两种模式

文岭南师范学院附属中学 罗东萍

一、问题提出

“韦达定理”在解析几何中是一个耳熟能详的名词，关于它在解析几何中的应用文章已经写得非常多了，查阅近20年关于解析几何中韦达定理应用的文献资料发现，这些文章基本局限于简化计算以及运算技巧，我们可换一个视角讨论韦达定理在解决高考试题中的应用。首先观察下面两例解析几何试题：

引例1和引例2有一个共同的条件“直线与圆锥曲线交于两点”，我们称之为“基本条件”， 时隔九年，这两道试题的“基本条件”雷同，不同的是已知直线的条件，因而，建立根与系数关系的方法和步骤完全一样：联立方程组，构造一元二次方程，韦达定理应用(建立根与系数的关系)。

有理由推断，如果将“基本条件”相同的试题归为一类，该类试题中直线存在的状态将影响韦达定理的应用。事实上，读者将会看到，根据直线的形态可将高考解析几何试题中韦达定理使用情形清晰分类。

二、两种模式

1.单参数模式

单参数模式意指仅已知题设“基本条件”中决定直线方程的一个条件，引例1和引例2皆为单参数横式，大量的高考试题亦属于这种模式。

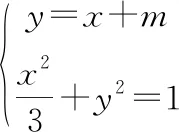
习惯上将例1中韦达定理的使用归为“设而不求”这一技巧，本质含意为：假设直线与圆锥曲线的交点，但在整个解题过程中并不需要具体求出交点；然而，单参数模式高考试题并非永远“设而不求”，有一类单参数高考试题需要利用韦达定理求出具体的交点，且极具技巧性。

2.双参数模式

双参数模式意指题设“基本条件”中决定直线方程的两个条件都未知，这类试题应用韦达定理有一定的难度。

解析：由于E，F是椭圆C上两个动点，直线EF的方程的两个参数未知，故属于双参数模式，构建一元二次方程、建立根与系数的关系需要一定的技巧，设E(x1，y1)，F(x2，y2)，直线EF的方程为y=kx+m；将直线EF的方程和椭圆C的方程分别变形为：

由此看到，对于双参数问题，不是将基本条件中的直线与圆锥曲线联立得到一元二次方程，而是将方程的变元改为其它形式，如本例变元是两点连线的斜率，此时，一元二次方程的解亦不是直线与曲线的交点；有时，对于双参数模式，有时构造一元二次方程并不需要联立方程组。