CCFD重叠网格并行算法设计和优化

刘夏真，袁 武，马文鹏，胡晓东，陆忠华，张 鉴

(1.中国科学院计算机网络信息中心，北京 100190;2.中国科学院大学，北京 100049;3.信阳师范学院计算机与信息科技学院,河南 信阳 464000)

1 引言

重叠网格(Overlapping Grid)[1]的基本思想是将计算区域划分为多个相对简单的子区域独立生成网格，子区域之间存在相互覆盖关系，重叠区域的流场信息通过插值进行匹配和耦合。重叠网格放宽了网格拓扑要求，能在刚性运动中保留初始网格品质，故而被广泛应用于研究诸如飞行器抛壳抛弹、级间分离、无人机旋翼、高铁会车、船舶操纵运动等[2 - 5]具有相对运动为主要特征的多体流体动力学问题，显示出独到优势。

迄今为止，国外发展的重叠网格程序有Pegasus[6]、SUGGAR[7]、DCF3D[8]、OVERGRID[9]、BEGGAR[10]等，在工程领域广泛使用的一些商业软件(如CFD++、FASTRAN等)也具备网格重叠功能。国内方面，中国空气动力研究与发展中心[11]、北京航空航天大学[12,13]、西北工业大学[14,15]、南京航空航天大学[16]等单位均发展了各自的算法和软件。早期的程序主要是串行计算代码，随着高性能计算在计算流体力学CFD(Computational Fluid Dynamics)领域的普遍应用，适应分布式环境的重叠网格装配算法受到了广泛重视[17,18]。

中国科学院计算机网络信息中心在国家和院所项目的支持下,在重叠网格并行算法和优化上开展了一些工作[19 - 21]，开发了计算流体力学并行计算软件CCFD(China CFD)。本文将简要介绍CCFD并行重叠网格方法，包括并行算法设计、负载平衡和通信优化等。

2 重叠网格的基本概念

首先，简要介绍重叠网格的基本概念，以空间中五球体为例，说明建立结构重叠网格的主要步骤[12]。

(1)对每个球体分别生成彼此覆盖的初始网格，如图1a所示。

(2)落入物面内部的网格点在流场计算中无实际意义，因此需要将这部分网格点屏蔽掉，一般记为“洞内点”，以区别于参与流场计算的网格点即“洞外点”。人们将标识洞内点的过程形象地称为“挖洞”，挖洞的结果即产生紧密围绕洞内点的初始洞边界，如图1b所示。

(3)挖洞产生的初始洞边界一般贴近物面，使网格重叠区域庞大，同时插值区流场梯度很大，一般在挖洞结束后需要对洞面进行一些优化，以改善洞面质量。洞面优化结束后，洞边界和紧邻的一层洞内点转换为插值边界，用于各子区网格的信息交换，如图1c所示。

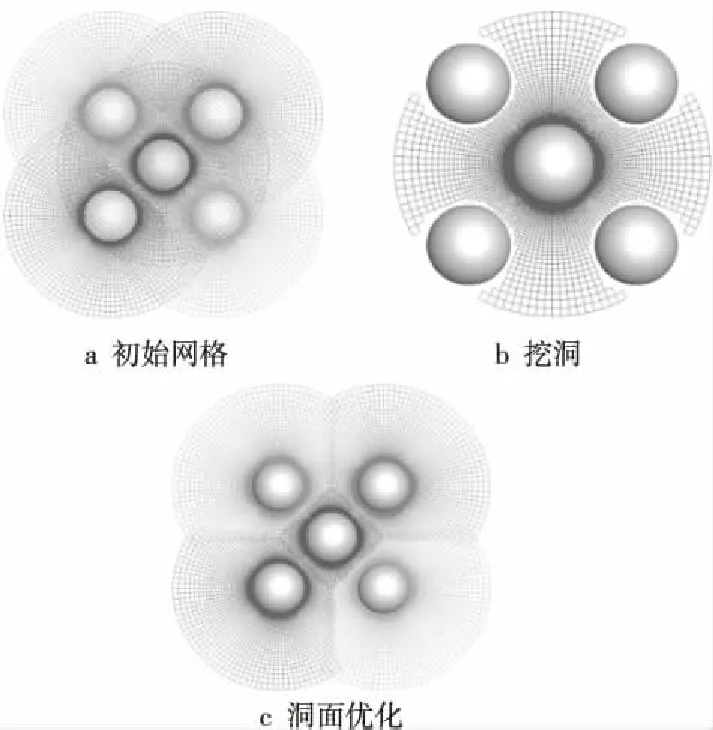
Figure 1 Schematic diagram of the overlapping process of five spheres in space图1 空间五球体重叠过程示意[12]

由上述内容可知，重叠网格研究的主要内容就是建立网格重叠关系，因此在分布式环境下建立高效、鲁棒的挖洞和洞面优化算法，是重叠网格并行算法设计关注的重点。此外，基于结构重叠网格体系的CFD求解器，在计算负载和数据通信上，也和一般结构网格求解器有所区别，结合重叠网格算法特点，设计良好的负载平衡模型和通信模式，是程序并行优化需要关注的重点。

3 网格并行装配算法

3.1 局部洞映射模型

常见的挖洞方法[22,23]有点矢法、射线求交法、洞映射方法、Object X-Ray、叉树挖洞方法等，其中，洞映射方法通过构建辅助的直角笛卡尔网格来近似物体的挖洞曲面，将点与曲面之间的关系转化为点与笛卡尔单元之间的简单关系，因此效率和自动化程度都很高，在Pegasus 5[24]中得到了应用。

传统的洞映射方法以整体物面的包围盒作为笛卡尔边界，这是比较直接的串行思维。在并行环境下，传统方法需要每个处理器搜集和处理所有几何体的全局物面信息，这种做法导致数据局部性较差、数据扩展性不强。CCFD设计了一种具有局部数据特性的洞映射方法，如图2所示，对几何体与其它网格块相交的局部物面构建笛卡尔近似，局部物面是分散于各个进程的、不封闭的物面，该局部模型可以在单独进程上进行填充和标识属性，而不依赖于其它进程，非常适合在分布式环境下计算。

Figure 2 Local hole mapping model图2 局部洞映射模型

局部洞映射模型是否合理，需要考虑物面不封闭引起的笛卡尔单元属性标识问题。传统方法在区分洞映射模型单元属性时，首先要确定“种子”单元属性，例如标记4个角区位置的单元为外部单元，再由角区向网格域内推进和填充。局部模型则由于物面的不连续、不封闭，缺少类似的先验信息。

考虑到洞映射模型作为自身计算域的映射，其内部单元对应计算域的物体内部，外部单元对应计算域的网格部分。因此，对于各个被分割的互不连通的洞外区域，如图3所示，笛卡尔网格的外部单元必然落在计算网格中，反之，计算网格也必然落在非内部单元(外部单元或边缘单元)，这是一个充分必要条件。

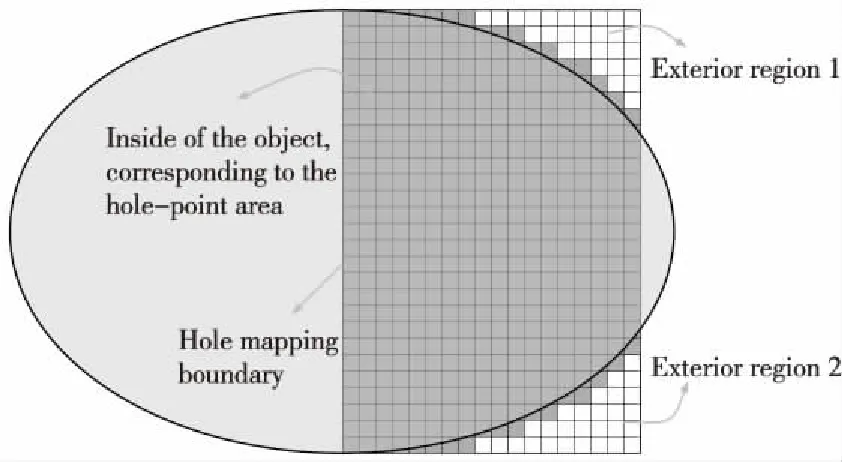
Figure 3 Relationship between local hole mapping model and computing grids图3 局部洞映射模型与计算网格关系

根据上述推断，CCFD设计了一种适用于局部洞映射模型的标识方法，如图4所示，首先，标记笛卡尔网格与物面相交的部分为边缘单元，见图4a。其次，对落入洞映射边界的计算网格进行下标计算，获得所有包含自身网格点的笛卡尔单元，这些笛卡尔单元必然是外部单元或边缘单元，且分布在各个分割区域，见图4b。最后，再依据外部单元的相邻单元一定是非内部单元进行递归扫描，即可识别所有外部单元。由于物面或局部连续或终止于边界，外部单元的扫描过程不会穿越边缘单元进入洞内区域，因此外部单元的扫描结束后剩余的未识别单元就是内部单元，见图4c和图4d。

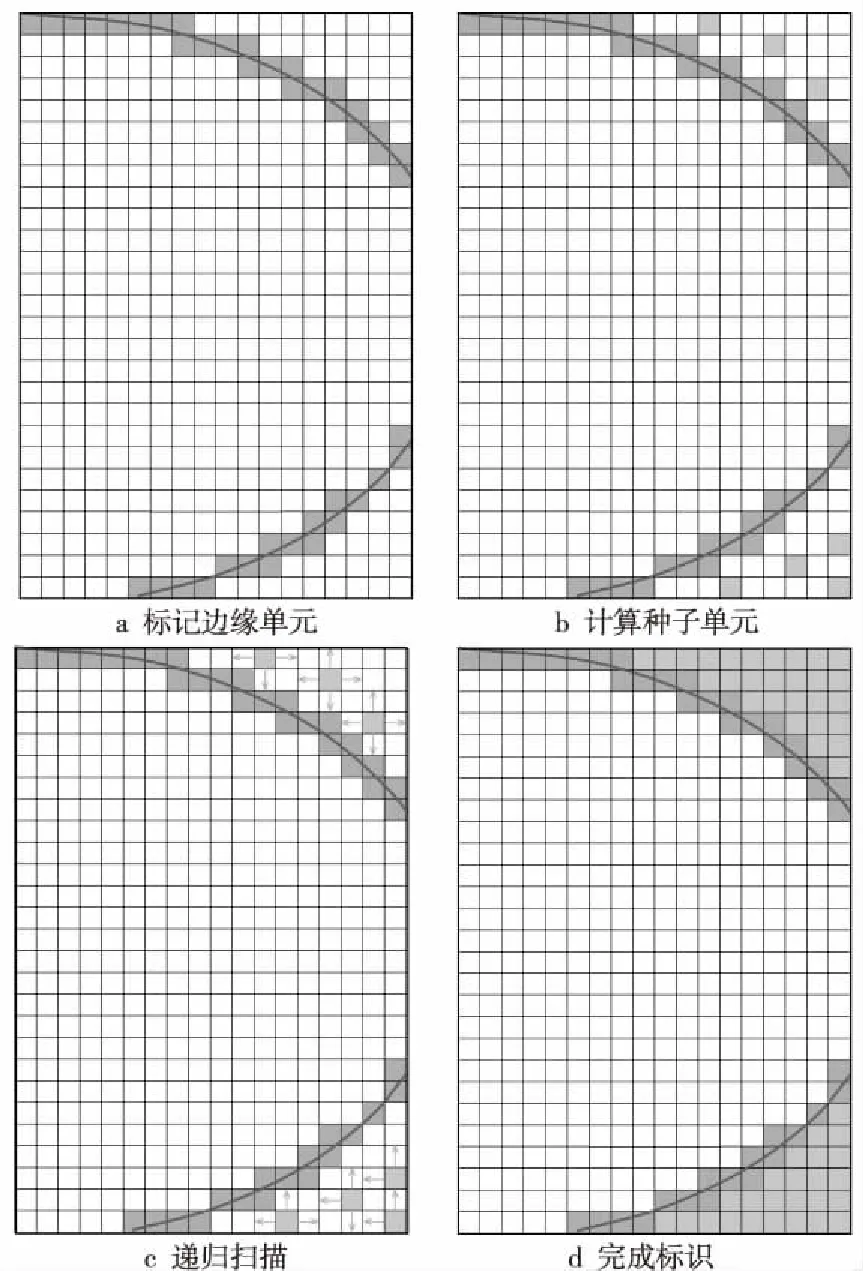
Figure 4 Mesh attribute identification method for local hole mapping model图4 局部洞映射模型的单元属性标识方法

3.2 隐式洞面优化

从几何图形学的角度看，洞边界的建立具有一定的随意性，只要能将落入其它物体内部的网格点“挖掉”就能达到屏蔽流场信息的目的。但是，对流场计算而言，如果直接将挖洞面作为洞边界，将使插值边界十分靠近物面的高梯度流动区域，严重影响流场解算精度。因此，需要在挖洞结束后对初始洞边界进行优化，常见的洞面优化技术[22,25]有阵面推进方法、割补法和隐式切割技术等。其中，阵面推进方法和割补法都是建立在迭代优化思想的基础上，适合于串行计算，算法并发度低，不利于并行扩展和应用。

隐式切割技术基于网格密度准则，对重叠区域内所有网格单元进行对比和判断，在一个轮次中完成网格重叠关系的建立，没有反复的迭代过程，因此十分适合并行计算。常用的网格密度判断准则包括网格单元体积、网格到物面的距离[25]等。CCFD设计了一种结合网格体积和壁面距离组合加权模型，如式(1)所示：

Q=1/(va·db)

(1)

其中，v为网格单元体积；d为网格到物面的距离；参数a和b可调节，比如选取a=1,b=0时即仅考虑网格尺度效应，选取a=0，b=1时即仅考虑物面距离的影响，不同参数的组合为设计人员调节网格品质提供了一个干预手段。

传统的隐式方法没有显式地区分洞内点和洞外点，认为无效的插值会被洞边界隔离，但必须要求洞边界连续、封闭。这一要求在处理缝隙、尖角等复杂形状或者网格质量较差时难以得到保证，有可能出现“挖进物面”的问题，即由于洞边界不连续，导致洞内区域和洞外区域错误地出现信息传递。CCFD采取的策略是，使用鲁棒性很高且并行性良好的局部洞映射方法进行初始挖洞，再使用隐式洞面优化方法对重叠关系进行调整和优化。CCFD将洞内点区分为2类，如图5所示，Ⅰ型洞内点是由挖洞产生的，落入物面内部的点；Ⅱ型洞内点是洞面优化过程中产生的被覆盖区域。前者被物面屏蔽，不在流场中，故不允许提取流场信息，这样就避免了出现无效插值点，完全克服了“挖进物面”的问题。

Figure 5 Two types of overlapping hole generated by flaps digging holes on the main wing grid图5 襟翼对主翼网格挖洞产生的2类洞内点

4 负载平衡和通信优化

4.1 两级负载平衡模型

计算网格的区域分解，是CFD并行计算的前提条件。常用的区域分解方法有递归二分法、平衡切割树法[26]、贪婪算法[27]、KL(Kerninghan-Lin)算法、遗传算法[28]等。结构网格划分的算法，主要是考虑了计算负载在各个处理器上的平衡，当通信时间的占比随并行规模增长而增加时，这种忽略通信开销的做法存在不足。特别是引入重叠网格后，跨结点的寻点、插值等操作，将加剧通信延迟的问题。

CCFD在结构网格区域分解中使用了多约束条件K-way图剖分算法[29]，设计了一种两级负载平衡模型[30]，同时将计算量和通信量作为衡量标准。首先，对原始非均匀网格块进行网格块分区，得到一系列规模更小、更均衡的子网格块集合，使用的方法包括递归边界二分法、固定步长法等；然后基于块分区后的子网格，建立一个以网格块为顶点、块内网格量和块间相邻面为顶点权重和边权重的有向加权图,基于此加权图进行图剖分操作，得到的每个集合的顶点权值之和近似，集合间的边权值之和均衡。将网格块集合分配到不同的计算单元上，实现网格块在处理器上的计算量和通信量负载均衡。

(2)

其中，N是几何体数量，ni是第i个几何体的网格块数量。

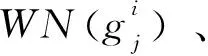
Figure 6 Directed graph of multi-block structure overlapping grid图6 多块结构重叠网格有向图

综合考虑有向图DG=V,E的通信量：

(3)

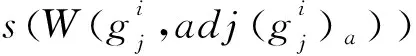
基于有向图DG=V,E的设计，CCFD针对多块结构重叠网格系统上提出的两级负载平衡模型如图7所示。在粗层，对原始非均匀大小网格块进行块分区处理，形成一系列规模更均匀、块数更多的子网格集合；在细层，对块分区后的子网格建立一个以计算量和通信量为顶点权重和边权重的有向加权图，使用多层图剖分算法实现加权图的分区，得到计算量和通信量均衡的集合，将集合映射到不同的处理器上，最终实现网格块在处理器上的计算量和通信量负载均衡。

Figure 7 Two-level load balancing model for multi-block overlapping grid图7 多块结构重叠网格的两级负载平衡模型

4.2 基于块的通信模式

多块结构重叠网格的通信比一般的结构网格更为复杂，不但有对接型网格块对的边界通信，还有在不同进程、相互重叠的网格块对的插值数据交换，因此需要结合算法特点考虑通信优化问题。Djomehri等[31]在对重叠网格求解器OVERFLOW的通信优化中，证实了采用非阻塞通信代替阻塞通信，可以有效降低插值数据交换的频次。在一个处理器负责多个网格块的情况下，以处理器为单位进行通信就必须等到一个处理器上所有网格块都计算完成后才能发起通信，这样通信过程独立于流场计算，通信时间无法得到隐藏，可能存在并行扩展性瓶颈。

CCFD结合应用特点对不同类型的进程间通信进行了优化，在计算过程中，存在诸如数据量小而频繁的数据通信、数据量大而次数固定的网格边界更新、一对多的广播数据、多对一的主从通信等，需要针对性地采用灵活多变的通信手段，包括集合通信、非阻塞通信等，以减少通信频次和数据量。此外，由于负载不均衡引起的进程等待问题也将产生很大的通信时间开销，CCFD采用了计算和通信重叠的方法，如图8所示，数据的发送和接收由后台处理，只在使用的时候才进行通信完成检测，这种方法可以有效隐藏通信时间。

Figure 8 Calculation and communication overlap mode图8 计算与通信重叠模式

重叠网格的并行插值计算具有局部性，即一个网格块需要的插值信息仅依赖于数个网格块，在同一时间步内，任何一个网格块的数据更新后都可以将更新信息发送出去，以供插值依赖块在下一个时间步来使用。因此，CCFD设计了以块为单位的重叠网格插值策略：每个处理器依次计算、更新若干网格块，在当前块的流场信息计算完毕后立即以非阻塞的通信发送给所插值依赖块所在的处理器，此部分通信的开销可以被该处理器上其他网格块的流场计算所隐藏。与以处理器为单位的通信模式不同，以块为单位的通信模式可能存在一个处理器与另一个处理器重复多次通信，但是可以实现通信和计算的完全异步，在大规模并行计算时能够有效隐藏通信开销。图9展示了Processor #0中的A和J网格块，Processor #1中的C和G网格块向Processor #2中的B、F、I网格块发送插值信息的过程。Processor #2按照信息来源的网格块号升序分配、组织接收缓存区，Processor #0和Processor #1中提供插值的网格块，按照目标块所在的处理器升序组织发送缓存区，保证同一网格块提供给同一处理器的数据连续存放。

Figure 9 Block communication mode:reorganization,sending,receiving processes图9 块通信模式：重组、发送、接收过程

5 测试与讨论

5.1 双机翼模型测试

通过开展双机翼模型在不同并行规模下的重叠网格测试，研究本文方法的计算和通信负载均衡特性。该模型采用2个平行布置的ONERA-M6机翼，图10所示为串行计算使用的粗网格和重叠结果示意，双机翼网格对称，插值边界居中，重叠区域整洁。采用CCFD软件包提供的网格划分工具SPLITTER，对串行计算的粗网格进行加密和分区，生成的并行计算网格规模约6 740万，网格块数量为5 080块，并行测试规模为64～1024核。测试环境是中国科学院计算机网络信息中心的高性能集群，每个结点配置2颗Intel Xeon E5520 CPU处理器，编译环境为Intel Fortran+OpenMPI。

Figure 10 Two-wing model and overlapping grids图10 双机翼模型和重叠网格示意

图11是双机翼模型测试的计算负载均衡因子CalFactor和通信负载均衡因子ComFactor随进程数变化情况。负载均衡因子定义为目标量的最大值/平均值，该比值越大，表示目标量均衡性越差。由图11可知，在进程数为64时，CalFactor和ComFactor分别是1.035和1.284，可知CCFD提出的两级负载平衡模型，通过考虑网格的重叠关系，使存在重叠关系的网格块在若干结点内聚集以减少通信开销，从而可获得良好的计算和通信负载均衡。当进程数从64增长到256时(以64核为基数扩展4倍)，CalFactor和ComFactor分别增长了1.294%和2.522%；进程数从256增长到1 024时(以256核为基数扩展4倍)，CalFactor和ComFactor分别增长了11.182%和7.040%，可见通过本文的方法，计算与通信负载在强扩展条件下仍然能维持较好的均衡水平。

5.2 机翼挂载分离测试

机翼挂载分离标模[32]被广泛用于考核非定常数值模拟方法和重叠网格方法。本文使用CCFD并行求解器研究了这一问题，该算例的粗网格规模约480万，分为22个子区域并行。计算条件和数值方法包括：来流马赫数0.95，模拟大气高度7.92 km，单位雷诺数7.874×106/m；层流计算，空间离散采用Roe’s FDS方法，非定常时间推进采用双时间步方法，时间间隔取Δt=0.65E-02。典型时刻流场和计算结果比较分别如图12和图13所示。图13是分离时间0.3 s内的3方向位移和姿态对比，图中实线是CFD计算数据，虚线是风洞实验数据，横轴是有量纲的时间轴，计算值和实验值符合良好。

创新理念和技术的缺乏，直接影响到了兽医行业的发展。对兽医技术进行创新，既能够提高企业效益，实现企业可持续发展的目标，又可以增强企业的综合竞争力，为新技术、新产品的研发提供动力，使企业与市场需求高度契合。另外，创新兽医技术，还与全球经济变革所提出的要求间存在着一定的联系，只有对技术、产品进行创新，才能紧跟经济发展的脚步，使相关产业的积极作用得以充分呈现。

Figure 12 Wing airborne separation model and typical moment flow fields图12 机翼挂载分离模型和典型时刻流场

Figure 13 Comparison of calculation and experiment value图13 计算和实验值比较

采用SPLITTER对在粗网格进行加密和分区，生成的并行计算网格规模约5 900万，网格块数量为6 940块(机翼网格为5 610块，挂载网格为1 330块)。扩展性测试规模为64～1024核，计算并统计了55个非定常时间步的结果，重叠网格装配过程在每个非定常时间步内重复进行。

图14所示是统计的重叠网格装配平均时间以及占非定常时间步的平均比值。由图14可知，重叠网格方法应用在多体相对运动问题仿真时，网格处理时间远少于流场求解时间，负载平衡模型应主要考虑流场计算部分。图15所示是并行计算加速比随进程数变化情况，以64核为基准的千核级并行效率达到了54.4%，说明CCFD在处理这类涉及非定常模拟和重叠网格计算的复杂多体相对运动仿真时，具有良好的并行效率和可扩展性。

Figure 14 Ratio of assembly time of overlapping mesh to unsteady calculation图14 重叠网格装配时间占非定常计算的比值

Figure 15 Parallel speedup ratio change with the number of processes图15 并行加速比随进程数变化

6 结束语

本文介绍了并行计算流体力学软件CCFD在重叠网格方法上的高效并行实现，包括：结合算法特点发展了具有局部数据特性的新型洞映射模型和适用于分布式环境的隐式洞面优化方法，设计了兼顾计算量和通信量的两级负载平衡模型，建立了基于网格块的通信模式并进行了调优。数值模拟结果表明，该方法对求解有相对运动的多体气动问题，具有良好的并行效率和可扩展性。

目前，国内高性能计算硬件平台发展迅猛，而相应的并行软件稍显不足。对于国产平台，不同硬件架构对同一模型算法的并行实现效率差别很大，并行软件只有协同国产平台的硬件环境开展设计和优化，才能充分发挥硬件性能。在下一步工作中，将瞄准国产E级异构平台，结合硬件特点开展算法的并行设计、代码移植和深层优化。