对高中教材平面向量基本定理的拓展
周如俊
(江苏省灌南中等专业学校,江苏灌南 222500)
对【题1】~【题4】及【例1】~【例5】有关形异质同的考题进行归类并拓展,形成平面向量基本定理中双变量λ,μ系数之间代数式求(最)值的问题:已知平面内某几何图形,常见为三角形、梯形、四边形、正多边、圆、圆锥曲线(椭圆、双曲线、抛物线)等图形上存在一组基底及任一向量点P一般在上述几何图形边上或内部区域变动)求表达式的(最)值(常数m,n∈R).本文在文献[1]有关概念基础上,结合有关试题,对高中数学教材中平面向量基本定理内容进行拓展,从“加、减、乘”三个思维视角对双变量λ,μ系数问题作简要探究.
【题1】(2020年江苏高考第13 题)如图1,在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC上,延长AD到P,使得若(m为常数),则CD的长度为__________.

图1

图2
【题2】(2013年江苏高考第10 题)如图2,设D,E分别是△ABC的边AB,BC上的点,AD=若为实数),则λ1+λ2的值为________.
【题3】(2017年江苏高考第12 题)如图3,在同一个平面内,向量的模分别为与的夹角为α,且tanα=7,的夹角为45°.若(m,n∈R),则m+n= .

图3

图4
【题4】(2009年安徽高考(理)第14 题)给定两个长度为1的平面向量和它们的夹角为120°.如图4,点C在以O为圆心的圆弧上变动.若则x+y的最大值是 .
一、“加”的思维策略
所谓“加”的思维策略,主要指利用平面向量的等和线性质,借助“数形结合”将具体的平面向量的双变量λ,μ系数之和mλ+nμ(最)值的运算转化为距离的长短的比例关系问题的解题策略.

图5

图6
(1)定值k的变化与等和线到点O的距离成正比,即
(2)当等和线l与直线AB在O点两侧时,k∈(-∞,0);当等和线l过点O时,k=0;当等和线l在O点与直线AB之间时,k∈(0,1);当等和线l恰为直线AB时,k=1;当直线AB在O点与等和线l之间时,k∈(1,+∞).
(3)当两等和线关于O点对称时,则固定值k互为相反数.
以图5为例作简证:
因点P在直线l0上,故平面向量基本定理知:λ+μ=1.
因O,P,P1三点共线,存在实数k使得故即kλ+kμ=k(λ+μ)=k.
因AB//A1B1,则由三角形相似比知:k=
等和线类考题求解思维策略是:若所求向量系数之和为λ+μ情况,先找出λ+μ=1 的直线l0,然后作l0的平行线(等值线)l,最后利用相似比k,求出λ+μ的值即可;若所求的向量系数之间是mλ+nμ线性关系,通过调节基底,使得所求表达式成为mλ+nμ两个新基底的系数和,在此新基底情况下,确定系数和mλ+nμ为1的直线l0情况,将l0平行移动到最值时等和线l位置,通过相似比k求出mλ+nμ即可.
对文前【题1】~【题4】试题求解作如下简析.
【题1】如图7 所示,本题关键是利用等和线定理求出PD、AD的长,再在△ADC中利用正弦定理求解即可.
两系数和为1 的等和线为BC,过A点作的等和线两系数和为
若D与C重合,则CD=0;若D与C不重合,则相似比从而可求PD=,AD=PA-PD=3=AC,从 而 在△ADC中,由正弦定理求出故CD=0 或

图7

图8
【题2】作图8 所示辅助线,易知DF为BG的中位线.等和线l(直线AF即直线DE)的两向量系数之和
【题3】【题4】分别作如图9、图10 所示等和线.

图9

图10
【题3】过C点作等和线l,则
【题4】过C点作等和线l(C点为圆O切点),此向量系数之和存在最大值:(x+y)max=
【例1】(2017年全国高考Ⅲ(理)第12 题)如图11,在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上,若则λ+μ的最大值为________.

图11

图12
【简析】作如图11 所示辅助虚线,两系数和λ+μ为1 的等和线为l0(即BD直线);最远的等和线为l(即直线P1P),此时(λ+μ)max=
【例2】(2013年杭州一模第17 题)如图12,在扇形OAB中为弧上一个动点,若则x+3y的取值范围是________.
二、“减”的思维策略
所谓“减”的思维策略,主要指利用平面向量的等差线性质,借助“数形结合”将具体的向量的双变量λ,μ系数之差mλ-nμ(最)值的运算转化为距离的长短的比例关系问题的解题策略.

图13
(1)同号的k值之比等于点O到等差线距离之比,即
(2)当等差线l与AM延长线相交时,k∈(-∞,0);当等差线l恰为直线OM时,k=0;当等差线l在直线OM与点A之间时,k∈(0,1);当等差线l过点A时,k=1;当等差线l与延长线MA相交时,则k∈(1,+∞).
(3)当两等差线关于OM对称时,则固定值k互为相反数.
以图13为例,作简证:
当点P与点M重合时则λ-μ=0;
当点P是直线OM(即l0)上异于O、M任意一点时,不妨设
当点P在与直线OM(即l0)平行的直线l上时故
等差线类考题求解思维策略是:若所求向量系数之和为λ-μ情况,先找出λ-μ的直线l0,然后作l0的平行线(等值线)l,最后利用相似比k,求出λ-μ的值即可;若所求的向量系数之间是mλ-nμ线性关系,通过调节基底,使得所求表达式成为mλ-nμ两个新基底的系数和,在此新基底情况下,确定系数和mλnμ为1的直线l0情况,将l0平行移动到最值时等和线l位置,通过相似比k求出mλ-nμ即可.
【例3】(2014年陕西高考(理)第18题)在直角坐标系xoy中,已知点A(1,1) ,B(2,3),C(3,2),点P(x,y)在△ABC三边围成的区域(含边界)上.
(1)略;
【简析】本题命题本质是基于等差线的内容背景而设计试题的,设BC中点为M,易求出三条平行线的直线方程(如图14所示).

图14
等差线为AM时:k=m-n=0,过C点等差线时k=m-n存在最大值,且kmax=m-n=
三、“乘”的思维策略
所谓“乘”的思维策略,主要指利用平面向量的“等积线”性质,借助“数形结合”,将具体向量的双变量λ,μ系数之积的λμ(最)值运算转化为利用等积线(双曲线)上(动)点与题设中向量几何(位置)之间关系问题的解题策略.
(1)当双曲线有一支在∠AOB内时,k>0.
(2)当双曲线两支都不在∠AOB内时,k<0.
建立如图15所示坐标系,x轴是∠AOB平分线,作简证:

图15
记点P坐标为(x,y),则从而有x=(λ+μt)a,y=(λ-μt)b,即
等积线类考题求解思维策略是:首先,确定(或画出)等积线(即双曲线)方程(图象),其次,借助等积线图象,数形结合速解有关求(最)值问题.
【例4】(2010年上海高考(理)第13 题)如图16 所示,直线x=2 与双曲线的渐近线交于E1,E2两点,记任取双曲线Γ 上的点P,若b∈R),则a、b满足的一个等式是______.
【简析】本题点P在以直线OE1,OE2为渐近线的等积线(双曲线),渐近线方程为y=点坐标为(2,1),E2点坐标为(2,-1),由等积线定理知:4×1×(ab)×22=4,即ab=

图16
【例5】(浙江省镇海中学2020 届高三5 月高考仿真测试数学试题)已知平面向量a,b,c,d满 足,a·c=b·c=0,c·d=0 ,若平面向量s=xa+yb(x,y>0 且xy=1),则的最小值是___________.
【简析】本题命题的核心是“s=xa+yb(x,y>0 且xy=1)”条件中隐含着等积线的性质内容,其中“t=1,λμ=1”.
因s=xa+yb(x,y>0 且xy=1),由等积线定理知:向量终点S(m,n)在等积线(双曲线)上(如图18).


图17
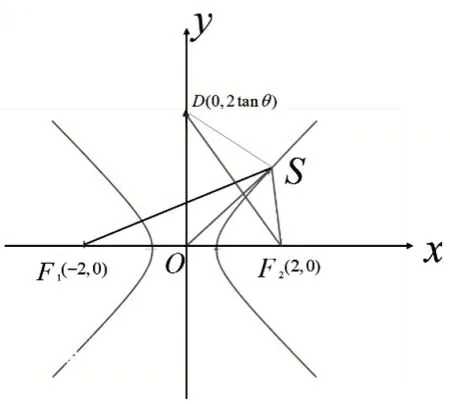
图18
事实上拓展平面向量基本定理还有等商线定理、等平方和线定理以及等和面定理,他们的性质也是命题者未来可能关注的拓展点,限于篇幅不再赘述.


