Ortho-SUV支架空间位姿建模与求解
傅 超, 范佳程, 王石刚, 梁庆华
(上海交通大学 机械与动力工程学院, 上海 200240)
骨折和肢体畸形是骨科最为常见的疾病,内固定治疗方式由于必须将肢体切开复位,增加了肢体创伤及被感染的风险,破坏了骨端愈合的微环境,会干扰骨骼的生理性愈合.而骨外固定技术具有适用范围广、固定可靠、微创、并发症少等优点,拥有许多内固定不可比拟的优势,越来越多地应用于治疗骨折和肢体畸形[1].苏联骨科医生Ilizarov在治疗中提出了“张力-应力法则”生物学理论,即生物组织被缓慢牵拉时会产生一定的张力,可刺激组织再生和活跃生长[2],奠定了骨外固定临床应用技术体系的基础.
现有的骨外固定器有Ilizarov支架和Taylor支架,见图1(a)和(b).其中,Ilizarov支架一次只能矫正成角、旋转、移位畸形中的一种,往往需要数次重新装配才能完全达到畸形矫正的目的.其治疗周期长,使患者多次暴露于辐射中,且数字化程度不高,需要大量的临床经验[3].Taylor支架是Stewart并联机构在骨科矫正方面的应用,虽然能同时矫正各种形式的畸形,但其装配要求较为严苛,杆件连接到骨骼固定环上的铰点需按一定规律布置.在实际治疗过程中,由于Taylor支架结构单一,缺乏灵活性,容易产生杆件与患肢干涉的情况,导致矫形无法进行,需要重新装夹,给患者带来痛苦,同时也增加了手术风险[4].

图1 各种骨外固定器Fig.1 Various kinds of external fixators
针对以上骨外固定器的缺陷,俄罗斯学者Leonid Solomin,Alexander Utekhin和Victor Vilensky共同提出了Ortho-SUV 支架[5],见图1(c).它是一种新型的骨外环形固定支架,能够在三维空间同时矫正肢体的成角、旋转及移位畸形并牢靠固定,是一种特殊的并联机构[6].Ortho-SUV支架装配更自由,杆件连接到骨骼固定环上的铰点可随意布置,且可以通过辅助固定环和Z型连接片,增大6根连杆所构建的矫形空间.而支架不至于过于庞大和笨重,结构灵活性高,使用方便,其独特的装配允许骨科医生借助它解决各种复杂的肢体畸形[7].
在骨折和肢体畸形治疗过程中,需要由Ortho-SUV支架的初始杆长正解得到动平台的初始位姿,通过畸形参数的测量转换得到畸形矫正完成后动平台的最终位姿,并通过最终位姿反解得到Ortho-SUV支架的最终杆长,从而得到治疗处方(即各连杆的调整量).关于Ortho-SUV支架的运动学求解尚未有相关报道,建立其空间位姿模型对于畸形矫正具有关键性作用.本文对Ortho-SUV支架的空间位姿进行了研究,并利用自行研制的Ortho-SUV支架进行了胫骨骨折矫形模拟实验,矫形效果良好,对于改善目前国内骨科医生大多凭临床经验治疗骨折、肢体畸形的现状和推进发展精准化、数字化的智慧医疗具有重要意义.
1 Ortho-SUV支架结构分析
1.1 基本结构——变铰点并联机构
如图2所示,Ortho-SUV支架由上下两个骨骼固定环(近端环、远端环)和6根连杆以虎克铰连接,两个骨骼固定环均分别只与3根连杆连接,其余3根连杆分别连接到相邻连杆的侧面.不同于Taylor支架,Ortho-SUV支架为变铰点并联机构,并非所有铰点均连接到骨骼固定环上,相邻连杆互相连接的铰点相对于骨骼固定环的位置可变.Ortho-SUV支架主要由以下部分组成[8]:
(1) 近端环(以下称为定平台).定平台与参考骨通过钢针和固定夹连接.
(2) 远端环(以下称为动平台).动平台与畸形骨通过钢针和固定夹连接.

图2 Ortho-SUV支架结构Fig.2 Structure of Ortho-SUV frame
(3) 6根连杆. 每根连杆由螺杆和长度变化单元组成,长度变化单元未锁紧时,旋转它可以调整虎克铰至长度变化单元末端的长度,即调整杆长.
在骨折或畸形两端的骨段上用钢针经软组织穿过骨结构,再使用连杆和固定夹将其连接固定在Ortho-SUV支架上.当6根连杆的长度逐渐发生变化,动平台的位姿因此而改变,与之固连的畸形骨随着动平台运动至解剖轴与参考骨解剖轴重合的位置,由“张力-应力法则”可知,组织将再生并活跃生长,即达到肢体畸形矫正的目的.
1.2 坐标系建立与空间位姿参数定义
图3所示为Ortho-SUV支架的机构示意图,该示意图和本文所述模型均适用于图1(c)和图2所示结构及各种Ortho-SUV支架的变形结构,后续将详细讨论.以逆时针方式给各连杆编号得1~6号连杆,1、3、5号连杆与定平台连接的各铰点分别为A1、A3、A5,2、4、6号连杆与动平台连接的各铰点分别为B2、B4、B6.其余各铰点分别为C1~C6,其下标与所在连杆的编号一致且互异于与之距离最近的铰点下标.杆长定义为该连杆实际铰点之间的距离,例如1号连杆的杆长为|A1C1|.建立定平台固定坐标系O-XYZ和动平台动坐标系O′-X′Y′Z′(见图3),其中固定坐标系O-XYZ的原点O为ΔA1A3A5的外接圆圆心,X轴垂直指向A1A3,Z轴竖直向上,由右手定则确定Y轴;动坐标系O′-X′Y′Z′ 的原点O′ 为ΔB2B4B6的外接圆圆心,X′ 轴垂直指向B2B4,Z′ 轴竖直向上,由右手定则确定Y′ 轴.

图3 Ortho-SUV支架机构示意图Fig.3 Sketch of Ortho-SUV frame
在以上坐标系基础上,使用欧拉角描述法描述动平台在固定坐标系O-XYZ中的位姿.当动坐标系沿固定坐标系的X轴、Y轴、Z轴分别平移x、y、z后,再在新的坐标系下绕Z轴旋转α角,绕Y轴旋转β角,绕X轴旋转γ角,则两坐标系之间的坐标变换矩阵为[9]

(1)
式中:矩阵R为按照Z-Y-X方式欧拉角旋转得到的旋转矩阵;向量P为动坐标系原点O′在固定坐标系O-XYZ中的坐标.若求得空间位姿参数{x,y,z,α,β,γ},则可描述动平台相对于定平台的位姿.
2 Ortho-SUV支架空间位姿建模
在使用Ortho-SUV支架进行肢体矫形时,医生需要测量其6根连杆的初始杆长Li(i=1, 2, …, 6)以及ΔA1A3A5和ΔB2B4B6的各边长,而Ortho-SUV支架的结构决定了AiCi+1(i=1, 3, 5)和BiCi+1(i=2, 4, 6)的长度相等,其表示为结构参数D,是已知量.当i=6时BiCi+1为B6C1,本文以下均采用此约定,即当i=6时,i+1=1;i=1时,i-1=6,以此类推.
设ΔA1A3A5的各边长分别为L13、L35、L51,ΔB2B4B6的各边长分别为L24、L46、L62,如图4所示,则ΔA1A3A5的外接圆半径R1为
(2)

图4 定平台和动平台坐标系Fig.4 Coordinates of fixed platform and mobile platform
由此可得Ai(i=1, 3, 5)点在固定坐标系O-XYZ的位置向量Ai=[AixAiyAiz]T为
(3)
θ1由ΔA1A3A5运用余弦定理可得
(4)
同理可得ΔB2B4B6的外接圆半径R2,Bi(i=2, 4, 6)点在动坐标系O′-X′Y′Z′ 的位置向量bi=[bix′biy′biz′]T以及θ2,不再赘述.因此,当给定ΔA1A3A5和ΔB2B4B6的各边长时,Ai和bi均为已知量.
由此可见,尽管Ortho-SUV支架装配多样化,但均可简化为图3所示的机构示意图,只需知道各连杆末端的铰点A1、A3、A5及B2、B4、B6之间的距离,即可确定ΔA1A3A5和ΔB2B4B6所在平面并得到各铰点在各自坐标系中的位置,且各铰点理论上可以呈任意三角形分布.
由式(1)可通过齐次坐标形式将Bi(i=2, 4, 6)点在动坐标系O′-X′Y′Z′的位置向量bi变换为在定坐标系O-XYZ的位置向量Bi=[BixBiyBiz]T,即
(5)
假设Ci(i=1, 2, …, 6)点在固定坐标系O-XYZ的位置向量为Ci=[CixCiyCiz]T,则在固定坐标系O-XYZ中第i根连杆可用矢量关系表示为
(6)
向量Li的模即是各连杆的杆长Li(i=1, 2, …, 6),该矢量关系可进一步表示为
(7)
通过6根连杆的杆长关系可得由6个非线性方程组成的方程组,即
(8)
(9)
方程组(8)即为Ortho-SUV支架的空间位姿模型.
3 空间位姿求解
3.1 位姿正解
类似于Stewart平台,空间位姿正解是指在已知Ortho-SUV 支架的杆长Li(i=1, 2, …, 6)、结构参数D、ΔA1A3A5和ΔB2B4B6的各边长的情况下,通过式(8)计算动平台相对于定平台的位姿{x,y,z,α,β,γ}.
由Stewart平台相关的研究可知,求解这样复杂的非线性方程组较难得到解析解,常采用数值方法求解,如牛顿-拉弗森法、逐次逼近法等方法[10].Stewart平台正解是以空间位姿参数{x,y,z,α,β,γ}作为未知变量代入带有三角函数的非线性高耦合方程组求解.与之不同的是,Ortho-SUV支架为变铰点并联机构,当其动平台位姿改变时,铰点Ci(i=1, 2, …, 6)相对于定平台的位置也会改变.若直接以空间位姿参数{x,y,z,α,β,γ}作为未知变量求解,由于Ci点不在动平台上,不能通过空间位姿参数将其坐标表示为固定坐标系中的坐标,无法求解得到Ci点.本文在进行Ortho-SUV支架的位姿正解时,直接以Bi(i=2, 4, 6)点和Ci(i=1, 2, …, 6)点在固定坐标系O-XYZ的位置向量Bi和Ci作为未知变量代入非线性方程组(8)求解.在求解得到Bi和Ci后,将其代入式(5),由bi和Bi通过广义逆矩阵的形式求解坐标变换矩阵T,即可求得矩阵T的各元素,进而得到空间位姿参数{x,y,z,α,β,γ}.这种求解方法将求解非线性高耦合三角函数方程组转化为求解不含三角函数的普通非线性代数方程组,降低了方程组求解难度,能更加简便快捷地进行求解.
以上方法在求解位置向量Bi和Ci的时候需要求解的未知数有27个,分别为[BixBiyBiz]T(i=2, 4, 6)和[CixCiyCiz]T(i=1, 2, …, 6),然而式(8)仅有6个方程,所以需要通过以下几何关系添加方程,即
(1)AiCi+1(i=1, 3, 5)和BiCi+1(i=2, 4, 6)的模长均为D.
(2)AiCi∥AiCi+1(i=1, 3, 5)且同向,BiCi∥BiCi+1(i=2, 4, 6)且同向.
(3) ΔB2B4B6的各边边长分别为|B2B4|=L24, |B4B6|=L46, |B6B2|=L62.
因此,将求解方程组(8)转化为求解如下非线性方程组:
(10)
使用MATLAB函数fsolve对以上非线性方程组进行迭代求解,即可求解得到Bi和Ci,进而得到空间位姿参数{x,y,z,α,β,γ}.其中Bi和Ci选取以下值作为迭代初值:
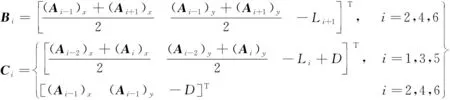
(11)
由于求解的是位置向量Bi和Ci的三维坐标分量,故迭代初值选取在相应的已知值Ai附近,能较快地收敛到符合当前实际情况的解,以下反解同理.
3.2 位姿反解
空间位姿反解是指通过式(8),在已知Ortho-SUV支架的空间位姿参数{x,y,z,α,β,γ}、结构参数D、ΔA1A3A5和ΔB2B4B6的各边长的情况下,计算Ortho-SUV支架的杆长Li(i=1, 2, …, 6).
由空间位姿参数{x,y,z,α,β,γ}和bi(i=2, 4, 6),通过式(5)可求得Bi.若能求解得到Ci(i=1, 2, …, 6)点在固定坐标系O-XYZ的位置向量Ci,将其代入式(6)和(7),即可求得杆长Li.
与正解类似,在求解位置向量Ci时需要求解的未知数有18个,即 [CixCiyCiz]T(i=1, 2, …, 6),需要通过以下几何关系寻找方程,即
(1)AiCi+1(i=1, 3, 5)和BiCi+1(i=2, 4, 6)的模长均为D.
(2)AiCi∥AiCi+1(i=1, 3, 5)且同向,BiCi∥BiCi+1(i=2, 4, 6)且同向.
因此,将求解Ci转化为求解如下非线性方程组:
(12)
使用MATLAB函数fsolve对以上非线性方程组进行迭代求解,即可求解得到Ci,进而得到杆长Li.其中Ci选取以下值作为迭代初值:
(13)
4 空间位姿求解验证
下面通过算例求解和胫骨骨折矫正模拟实验两方面对上述空间位姿模型及其正解与反解的正确性进行验证.
4.1 算例求解
三组算例见表1,验算时首先由杆长Li(i=1, 2, …, 6)根据式(10)进行空间位姿正解计算, 然后把计算结果作为反解条件,根据式(12)得到反解结果Li.各算例中,L13=L35=L51=L24=L46=L62=200 mm,结构参数D=15 mm.由表1可见,正解条件数据与反解结果数据相对误差小于0.01%,由此可见模型建立及求解方法正确.此外,以表1中反解的第一行数据为例,当已知位姿为{-0.001 3, -0.000 8, -127.546 7, 60.000 1, 0, 0}时,反解计算杆长,以式(13)作为迭代初值仅需迭代8次即可得到方程组的解,而直接以0作为迭代初值则需迭代18次,详见表2.这是因为迭代初值选取在已知铰点的坐标附近,故收敛较快.若都以0作为迭代初值,迭代次数更多,且有可能导致收敛到其他解,更糟糕的是可能不收敛.
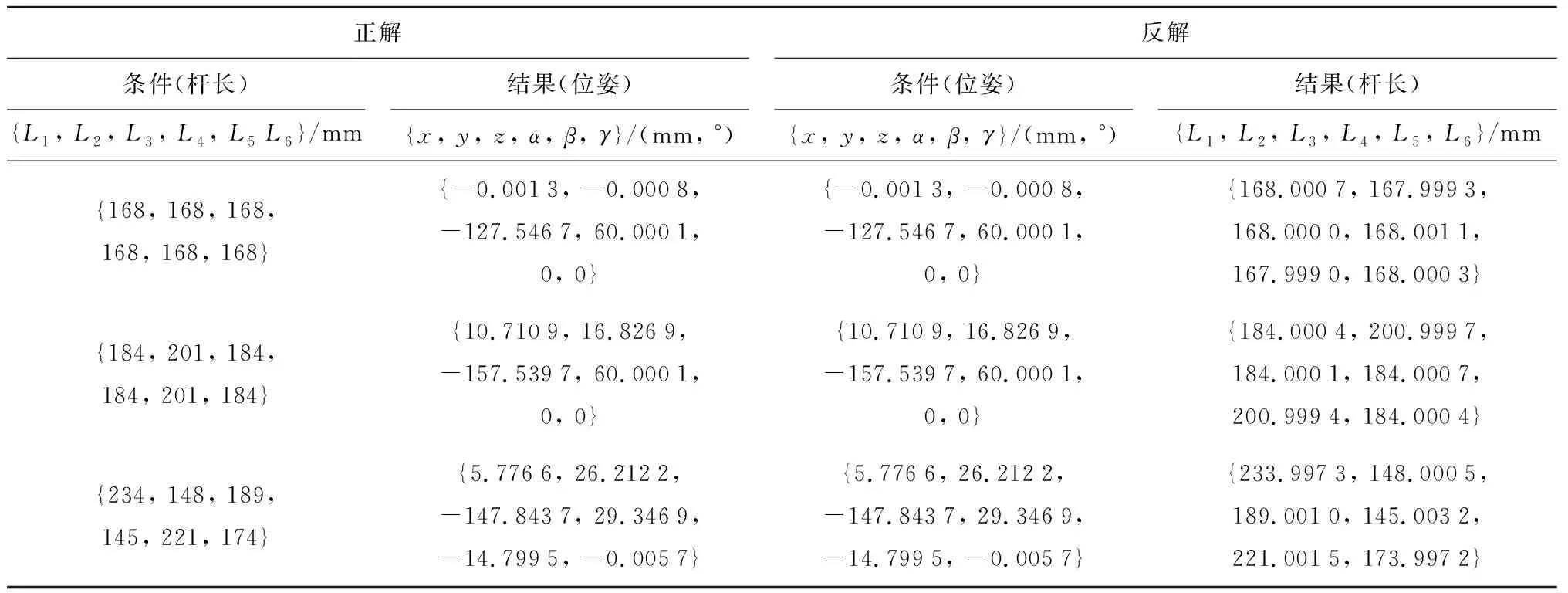
表1 空间位姿模型正解与反解算例Tab.1 Forward and inverse solution examples of spatial pose model

表2 不同迭代初值的反解算例

图5 初始畸形状态Fig.5 Status of initial deformity
4.2 胫骨骨折矫正模拟实验
胫骨骨折是外科创伤中最常见的骨折之一,以下进行胫骨骨折矫形模拟实验,使用数码相机对胫骨模型进行正位和侧位拍摄像片代替X光片,放置标尺作为测量参照物,设定畸形骨为左下肢胫骨.初始畸形状态见图5,测得支架初始6根连杆长度Li(i=1, 2, …, 6)分别为:136.5,165,168,120,155,156 mm;ΔA1A3A5和ΔB2B4B6的各边长为L13=167 mm,L35=171.5 mm,L51=190 mm,L24=186 mm,L46=201 mm,L62=170 mm,结构参数D=15 mm;由自行开发的矫形软件测得安装参数为:轴位参考环中心位于起点近侧32 mm;畸形参数为:内翻10.9°,外侧移位25 mm,屈曲10°,前部移位10.5 mm,轴位过长11.9 mm.通过初始杆长采用本文所述模型正解得到Ortho-SUV支架的初始位姿,结合安装参数和畸形参数得到最终位姿,并反解得到最终杆长Li分别为:141.8,133.3,146.6,130.9,144.0,158.9 mm.按该结果调整Ortho-SUV支架各连杆长度,矫形后效果如图6所示.

图6 矫正完成后的状态Fig.6 Status after completion of correction
模拟矫正后上下骨段解剖轴夹角小于0.5°,上下骨段间隙小于1 mm,其矫形效果完全达到了骨折矫形要求.
5 结论
(1) 以矢量建模方式对新型变铰点并联机构Ortho-SUV支架进行运动学分析,建立了其空间位姿模型,该模型适用于各种装配形式的Ortho-SUV支架.
(2) 进行空间位姿正解和反解,求解方法不同于一般Stewart并联机构,不涉及高耦合三角函数方程组,且迭代初值易于选取,准确有效地完成了该模型的求解,并通过算例及胫骨模拟实验验证了其正确性.
(3) 模型为Ortho-SUV支架用于骨折和肢体畸形治疗提供了理论支持,结合其结构灵活、矫形空间大等优点能给患者带来更方便、精准的治疗,对于推进我国智能化骨科矫形医疗的发展与进步具有重要价值.

