船体三维曲板展开方法多目标优化模型
兰宏凯, 柳存根, 聂 鑫
(1. 上海交通大学 海洋工程国家重点实验室, 上海 200240;2. 上海交通大学,高新船舶与深海开发装备协同创新中心, 上海 200240;3. 大连船舶重工集团有限公司, 辽宁 大连 116021)
随着国内船舶建造水平的不断提高,各大船厂逐步实践绿色造船、精益管理和无余量造船等先进理念.同时,船舶设计水平的提高,造成船体曲面日趋复杂,船体外板中曲板占比也逐步提高,对船体外板成形提出了更高的要求.船体放样是船舶建造过程的重要环节,为钢板号料套料工艺环节提供依据,是实现无余量造船的关键步骤.目前,船厂采用的放样方法大多为手工放样或计算机模拟手工放样,误差大并且效率低[1],往往需要留有一定余量.因此,需要更加精准的船体三维曲板放样展开方法,以提高造船效率,降低造船成本.国内外学者对船体三维曲板的展开方法进行了研究.Hinds等[2]提出以四边形网格对曲面进行划分,然后将各个单元进行展平获得有缝隙的展开曲面.Azariadis等[3]在Hinds的理论基础上进行了改进与探讨,减小了曲面展开的裂缝几何尺度.Wang等[4]利用Tendon Node Mapping (TNM)和Diagonal Node Mapping (DNM)算法实现对三维曲面的高效网格划分,通过能量法对三维曲面进行展开.Shin[5]对三维曲面进行微分逼近并进行初步展开,然后利用能量展开方法对展开方案进行优化,得出最终的展开方案.Seong等[6]将待加工板曲面和最终目标曲面间的差异曲面定义为工作面,用三角形或四边形单元将工作面进行几何分化,将离散后的单元进行展开,可以获得曲面展开后的平面.张雪彪等[7]通过导向单元条和改进肋骨弯度等方法提出船体复杂曲面的展开方法,可以为水火弯板成形提供收缩量.李纯金等[8]通过自适应算法对曲面展开过程中的网格细分进行了研究,为曲面展开提供支持.刘寅东等[9]运用参数化三维实体建模解决船体外板展开问题,并开发了相关软件程序.然而,船体三维曲面展开是造船的中间环节,为曲板放样和曲板加工等多个后续工艺环节服务,因此,对曲板展开效果的评价应该是多维度的,曲板展开方案的确定也应综合考虑后续工艺环节而确定.本文基于单元等长的船体曲板展开方法,采用面积误差、平均应变能和边缘线性3个评价指标,利用文化基因算法(MA)对船体三维曲板展开方案进行了多目标优化分析.
1 问题描述
三维曲面一般可分为平面、直纹面和复杂曲面,从可展性方面可分为可展曲面和不可展曲面.而船体曲板大多为不可展开的复杂曲面,需要将其分割为多个微小单元以逼近原曲面,然后再将各个微小单元进行展开,获得最终的近似展开平面.在不可展曲面的展开过程中,常见的展开思想有保证面积恒定,保证长度恒定和保证角度恒定等.目前,船厂中主要采用手工测地线法、垂直准线法和撑线法等展开三维曲面,其本质的展开思想均基于保证展开单元的长度恒定.结合工程实际情况,针对以帆型板为代表的大型板材,采用基于单元等长的展开方法,展开过程如下.
(1) 拟合待展曲面并划分网格.肋骨型线图中获取的数据点较少,需要通过做非均匀有理B样条(NURBS)曲面拟合对数据进行插值,同时将三维曲面进行网格划分,选取四边形网格.
(2) 计算线准线.纵向基准线为某条肋骨型线,横向基准线为贯穿曲面的一条空间曲线.要求横向基准线在展开图中为一条直线,因此横向基准线应为曲面内两点间的最短面内的距离.通过 Dijkstra 算法在三维曲面中迭代搜索,最终获取两点间的曲面最短距离,从而确定横向基准线.
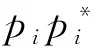
(4) 展开其他单元.如图1(b)所示,以确定四边形单元Ai,iAi-1,iAi-1,i+1Ai,i+1为例,介绍一般四边形的单元展开过程.已知四边形单元中Ai-1,iAi-1,i+1和Ai-1,i+1Ai,i+1已确定,需要确定点Ai,i的位置.根据单元等长的展开准则,在展开平面内找到一点Ai,i使得Ai,iAi-1,i和Ai,iAi,i+1在展开前后的长度恒定,由此即可确定点Ai,i的位置.

图1 展开过程示意图Fig.1 Example of expanding operator
问题假设:三维曲板在加工成形过程中,厚度恒定不变.三维曲板加工和曲板展开互为逆过程,在多支点冷压加工或部分水火弯板加工情况下,三维曲板展开前后上下表面积基本保持恒定.
基于单元等长的曲板展开方法所获得的展开方案取决于两条基准线的选择,即纵向基准线的选取和横向基准线的端点坐标决定了最终展开方案.在工程实际中,曲板展开后会进行套料号料的工艺过程,在套料过程中更希望板材的四周边缘为直线,可以方便切割并提高板材的利用率,因此要求曲板展开的形状边缘具有一定的线性水平.曲板展开图是曲板成形的基础,曲板展开过程中单元应变能在一定程度上可以反映曲板成形过程中的加工工作量,因此从减少后续加工成本的角度出发,要求曲板展开方案的单元应变能处于低水平.基于问题假设,曲板展开前后面积误差也是衡量展开方案的重要指标,希望面积误差控制在较低水平.
2 数学模型
基于以上对问题的描述和假设,提出船体三维曲板展开优化分析的数学模型.根据以上分析,可以通过曲面展开前后的面积误差、展开曲面边缘线性和展开曲面的单元平均应变能3个维度评价展开方案.
面积误差指标ΔA采用展开曲面面积与原三维曲面面积相对误差的绝对值表达.面积误差指标有效地反映出展开后的曲面面积与三维曲面面积的误差,从问题假设出发,面积误差越小展开效果越良好.
(1)
式中:Au为三维曲面面积,Ao为展开曲面面积,两者均通过微分单元累加求解.
(2)
(3)

(4)
(5)
(6)
式中:εib为面内弯曲应变矩阵;εs为剪切应变矩阵;σib为面内弯曲应力矩阵;σs为剪切应力矩阵;D为弹性矩阵;A为单元面积.
计算展开曲板平均单元应变能如式(4)所示,其中M为单元数.
(7)
由上述分析可得船体三维曲板展开优化问题的目标函数为
(8)
maxf2=maxρ(X,Y)
(9)
(10)
s.t.
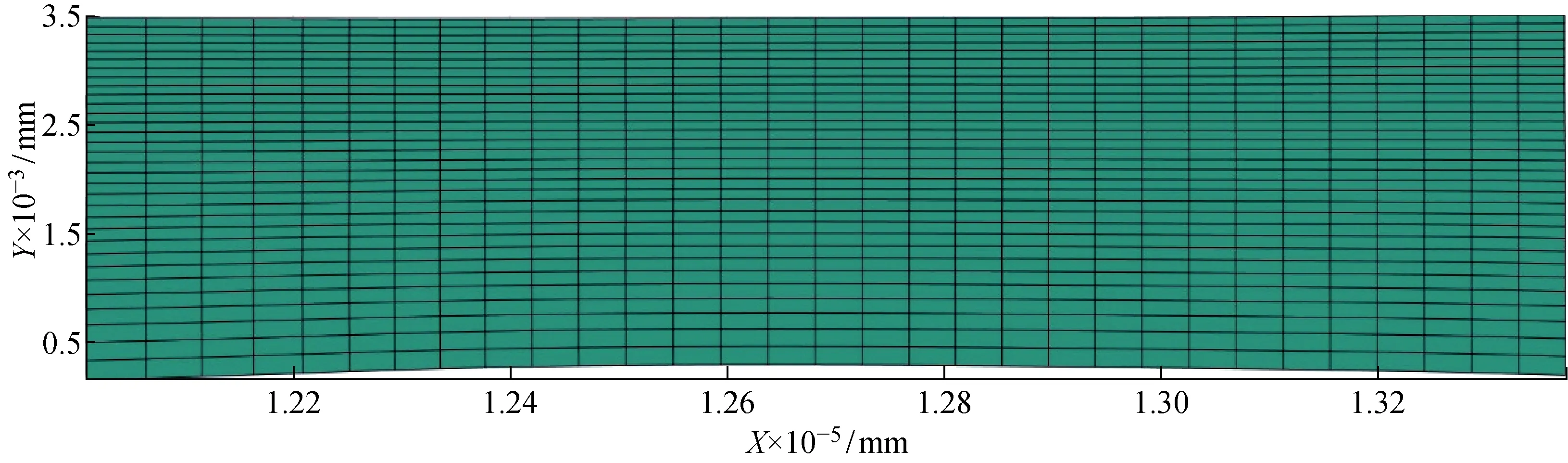
minp(i) (11) (i=x,y,z) minp(i) (12) (i=x,y,z) Num∈{1,2,…,RIBNmax} (13) 式中:minp(i)为待展开曲面单元节点i坐标的最小值;maxp(i)为待展开曲面单元节点i坐标的最大值;i为坐标轴编号,分别取为x,y,z;plef(i)为横向基准线左端点的i坐标值;prig(i)为横向基准线右端点的i坐标值;Num为纵向基准线所选取的肋骨型线编号,规定将肋骨型线按照肋骨型线图从左至右进行编号;RIBNmax为肋骨型线图中的最大编号. MA是在种群全局搜索的基础上与基于个体的局部搜索有效结合,在保持了遗传算法优秀的全局搜索能力的同时,提高了算法的局部搜索能力.近些年MA得到了广泛应用,求解包括生产调度[10-11]及其他工程领域的相关问题,如路径规划[12]、资源分配以及特征选取等.本文提出一种多目标MA(MOMA)以求解船体三维曲板展开的优化分析问题.作为多目标进化算法,MOMA基于Pareto最优概念进行设计.MOMA采用二进制编码,引入启发程序生成初始解,并基于二进制编码设计了交叉、变异等遗传操作以及局部搜索算子.下面对MOMA解的表达、种群初始化、遗传操作和局部搜索等内容进行详细描述. 为了提高初始种群质量,设计了启发程序,用于生成初始解.启发程序采用船厂经典测地线法对板材进行展开,获得最终的展开板.测地线法的展开思想与本文一致,因此可以获取测地线法展开的横纵基准线的信息,并采用二进制对其进行编码,产生启发程序初始解.基于该初始解,保持横向基准线端点不变,以初始解选取肋骨作为横向基准线,产生新的启发初始解.为了确保初始种群的多样性,要求启发式初始解的个数不超过种群规模的10%. 采用二进制编码表达3个决策变量,在初始化、交叉和变异过程中,对于超出边界的值需要重新进行计算,直到所获得的解在可行域范围内. 选择、交叉和变异是用于生成子代种群的遗传操作.选择操作采用基于非支配等级和拥挤距离的二元锦标赛方法,从父代种群中选出优秀个体进行遗传操作.二元锦标赛法的具体过程为对于非支配等级不同的两个个体,优先选择非支配等级低的个体;对于非支配等级相同的两个个体,优先选择拥挤距离大的个体;对选出的父代个体按概率P进行配对交叉.交叉操作采用部分交叉映射策略,具体操作如图2所示(该图为示意图,实际染色体长度较长),其中R为染色体位置.其具体步骤如下: 步骤1在父代1和父代2的染色体上选取相同位置(R1,R2). (1)强调团队协作,营造和谐氛围,保证职责分明而不影响亲和力,确保全体员工均能全身心投入。首先,应形成良好的合作意识,保证日常住宿与饮食,并提高自身责任心,同时,在不影响日常工作的基础上,丰富业余生活,以此进一步提高凝聚力。 步骤2交换父代1和父代2被选取的部分染色体,产生子代1和子代2. 步骤3对子代1和子代2进行解码,对于超出可行域的解随机赋值,对子代染色体进行修正. 图2 交叉操作示例Fig.2 Example of crossover operator 为了保证种群的多样性,对交叉操作产生的子代按概率实施变异操作,选取子代染色体中的位置,将其取反,并重新检验染色体是否越界. 在MOMA中,按照概率Ppart对个体施加基于模拟退火算法的局部搜索算子.模拟退火算法是借鉴固体退火原理,固体内部温度较高时,内部粒子运动快速无序;而随着温度的降低,固体内部粒子运动逐步趋向有序,最终达到稳定状态.模拟退火算法是一种贪婪算法,搜索过程中引入了随机因素,以一定的概率接受较差的解,可以帮助算法跳出局部最优,更可能实现全局最优解. 局部搜索算子的具体步骤如下: 步骤1以概率Ppart判断是否对个体Ti进行局部搜索. 步骤2若进入局部搜索算子,设置模拟退火算法基本参数,对个体Ti进行解码,随机产生个体Ti的邻域集合. 步骤3对邻域集合进行二进制编码,计算邻域集合的适应值集合,并计算其支配等级和拥挤距离. 基于以上对MOMA的介绍,可以获得算法的流程图,如图3所示.其中:g为种群代数;nFEs为循环算子;nFEsmax为种群中的个体总数. 图3 MOMA流程图Fig.3 Flow chart of MOMA 以船体建造过程中一块帆型板为例,应用上述算法对其进行展开优化分析,板材的型值表如图4(a)所示.其中:W为水线;L为肋骨线距离船尾的距离.NURBS曲面对该帆型板进行曲面重构和网格划分,网格单元为四边形,共划分 6 100(100×61)个网格,如图4(b)所示. 设置种群大小为60,迭代次数为100次,交叉概率为0.6,局部搜索概率为0.1;退火算法选择初始温度为800 ℃,温度位移系数为0.2,温度降低速率为0.9.应用MOMA对上述帆型板基于单元等长的曲板展开方法进行优化分析,为了验证算法的有效性,采用测地线法对同一块板材进行展开.此外,分别设立无启发算子和无局部搜索的算法进行对照计算,从而验证启发算子和局部搜索算子的有效性. 对采用由优化算法获得的解集,剔除非支配解后以支配等级和拥挤程度为指标进行排序,从支配等级为1的解集中采用线性加权法选择最终的方案.设置权重为[0.3,0.5,0.2],选择3个评价指标为[0.035%,8.84×10-4,0.698 1]的方案. 从表1中可以看出,采用优化方法获得的展开方案的面积误差、平均应变能和边缘线性3个指标均优于测地线法,说明通过优化获得的展开方法全面优于测地线法,验证了该优化算法的有效性.采用相同的权重对无局部搜索算子和无启发算子两种算法求解出的方案进行选择,结果如表1所示.无局部搜索算子的优化方法得到的展开方案面积误差和平均应变能指标均与优化方法有较大差距,从而说明局部搜索算子可以有效地帮助优化方法跳出局部最优,提高搜索效率,获得更为优质的解.由无启发算子优化方法得到的方案的3项指标与具有启发算子获得的方案的优化方法差距不大,这是因为所提算法为改进的多目标遗传算法,具有一定的随机性,而在迭代次数相同和种群数目相同的情况下,具有启发算子的优化方法得到优质解的概率更大. 表1 曲面展开计算结果Tab.1 Results of expanding operators 针对该帆型板,应用上述优化展开算法独立运算20次,可以获得多组计算方案,剔除支配解后形成新的解集合.应用AHP法对多组展开方案机型选择,最终获得方案.AHP法是美国运筹学家 Saaty 等[13]提出来的一种定性分析和定量分析相互结合的评价决策方法.通过建立问题的层次结构模型、形成各层的判断矩阵、进行层次单排序及一致性检验、进行层次总排序及一致性检验4个步骤来完成权值的确定. (14) 采用AHP法在非支配解集中选取最终的展开方案,输入AHP法的目标权重矩阵,本例输入值如式(14)所示,计算所得的3个目标对应的权重为[0.549 9,0.240 2,0.209 8],选择出最终方案为左端点坐标(1.20×105, 2.98×103, 1.93×104),右端点坐标(1.34×105, 2.91×103, 1.91×104),以及纵向基准线为11号肋骨,该方案的面积误差为 0.026 5%,边缘线性为 0.662 8,平均应变能为 9.04×10-4.该方案的最终展开图如图5所示. 图5 展开平面图Fig.5 Expansion plan 本文针对船体三维曲板展开问题,提出基于单元等长的展开方法,并基于该方法建立船体三维曲板展开优化问题的数学模型.以面积误差、平均应变能和边缘线性为目标,应用MOMA对曲板展开问题进行了多目标优化,通过与测地线法进行对比验证了该优化算法的有效性;通过设立对照算法试验,验证了算法中局部搜索算子和启发算子的有效性.考虑了船体曲板展开的后续工艺环节设置3个优化目标函数,所获得的展开方案是综合考虑板材号料套料和板材成形工艺需求的结果,为船厂无余量造船进程中的曲板展开放样提供一定的参考.3 多目标MA
3.1 种群初始化
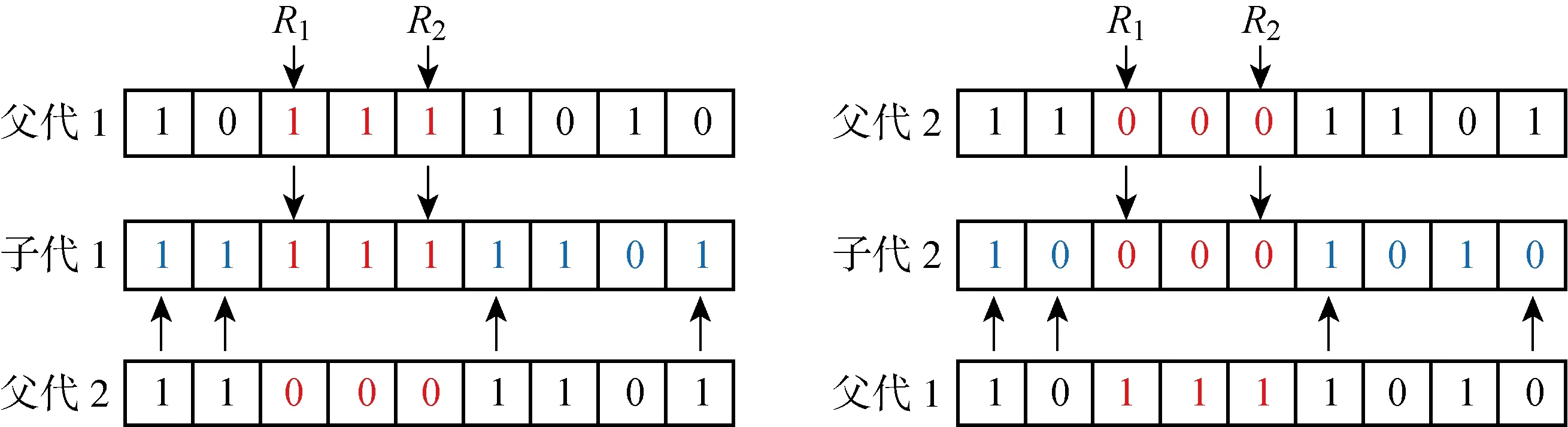
3.2 遗传操作
3.3 局部搜索算子
3.4 算法流程

4 展开实例

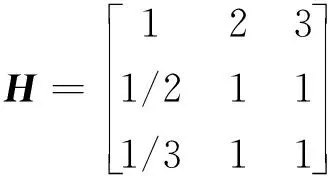
5 结语

