开孔冷弯薄壁C型钢压弯构件的数值分析和设计方法

任 重， 刘秋婷， 王斌华， 戴柳丝

(1. 上海大学 土木工程系， 上海 200444； 2. 同济大学 土木工程学院， 上海 200092)

冷弯薄壁型钢构件因自重轻、强度高、便于施工等优点，常作为承重构件、附属结构等广泛应用于住宅、商业和工业建筑中.但是，稳定性一直是影响冷弯薄壁型钢构件承载力的关键因素.局部、畸变和整体屈曲是冷弯薄壁型钢构件常见的3种屈曲模式[1-2].由于冷弯薄壁型钢构件截面形式的复杂化、开孔形式的多样化，极限强度和破坏模式可能会受这3种屈曲模式之间相互作用的强烈影响，使结构设计不安全.近年来，国内外学者针对屈曲相互作用开展了一系列研究[3-8].Camotim等[3-4]采用数值分析方法对局部-畸变、畸变-整体的屈曲相关作用进行了研究，修正了现有的直接强度法(DSM)设计公式.Dinis等[5]通过试验和数值分析详细讨论了固支情况下卷边槽钢的屈曲后强度特性以及破坏模式，结果表明翼缘的运动导致了局部-畸变屈曲的相关作用.何子奇等[6-7]使用试验和数值模拟的方法研究了畸变-局部屈曲的相关作用，对DSM畸变屈曲计算公式的非弹性段进行修正，并对承载力计算公式提出了相应修正建议.现有研究主要以畸变-局部屈曲相关作用为主，然而局部屈曲造成构件的破坏多发生在长度较短的受压构件中；对于中长冷弯薄壁型钢构件，畸变和整体屈曲对于构件的破坏影响更大，但其典型变形特征、失稳和破坏机理尚未完善，开孔的影响机制也尚未明确，因此有必要深入开展此方面的研究.

构件腹板开孔可使电线、管道方便通过，同时可降低结构自重.但开孔会导致应力重分布，对截面特性、构件截面承载力、屈曲失稳模态有重要影响.近年来众多学者对腹板开孔的冷弯薄壁型钢构件进行了研究[9-13].王春刚等[11]发现开孔构件的极限荷载低于无孔构件，且非纯弯状态的极限荷载下降幅度大于纯弯状态.Yuan等[12]提出采用简单的理论公式来评估开孔尺寸对腹板圆孔槽钢截面梁临界应力的削弱.但是，以上研究并未完全涵盖开孔的尺寸和位置(无孔、腹板跨中处开孔、腹板连续开孔)以及形式带来的影响，其结果不能广泛适用于各种形式的截面和开孔.另外，我国《冷弯薄壁型钢结构技术规范》[14]并没有对腹板开孔构件提出具体的设计规定.因此，对腹板开孔冷弯薄壁构件稳定性和承载力的研究具有重要意义.

C型冷弯内卷边槽钢和普通热轧槽钢相比，同等强度下可以节省30%的材料，不仅具有自重轻、强度高的特点，还具备了较高的稳定性.徐宏艳[1]对腹板开孔的冷弯薄壁C型钢构件稳定性进行了研究，提出了开孔梁开孔优化方案以及提高承载力的构造措施.本文运用有限元分析软件Abaqus对180根腹板开孔冷弯薄壁型钢C型截面绕强轴的单向压弯构件进行弹性和弹塑性分析，研究开孔形式、大小、位置对其极限承载力和破坏模式的影响.将数值分析结果与已有试验数据进行校对，对现有的无孔轴压冷弯薄壁型钢构件的DSM公式进行了合理修正.

1 有限元模型建立

1.1 构件尺寸设计

为了研究偏压作用下的开孔尺寸、位置、形式对腹板开孔冷弯薄壁C型构件失稳和破坏机理的影响机制，对180根构件进行数值建模并分析，包括3种截面形式、6种构件长度、3种开孔形式和2种开孔率.其中长度为 1 500、1 800、2 100 mm的构件具备连续开孔和跨中腹板单一开孔的形式.以C200-60-20-2-1500截面为例，截面尺寸和开孔形式如图1所示，图中d为沿腹板宽度方向的最大开孔尺寸.为方便分类，对构件进行统一命名，编号规则如图2所示，开孔形式Co、O、R和SC、SO、SR分别为连续的圆形、椭圆、矩形开孔和跨中的单圆、单椭圆、单矩形开孔.开孔率(P)以开孔沿腹板宽度方向的最大尺寸与腹板宽度的比值定义，0.4和0.6表示开孔率分别为40%和60%.

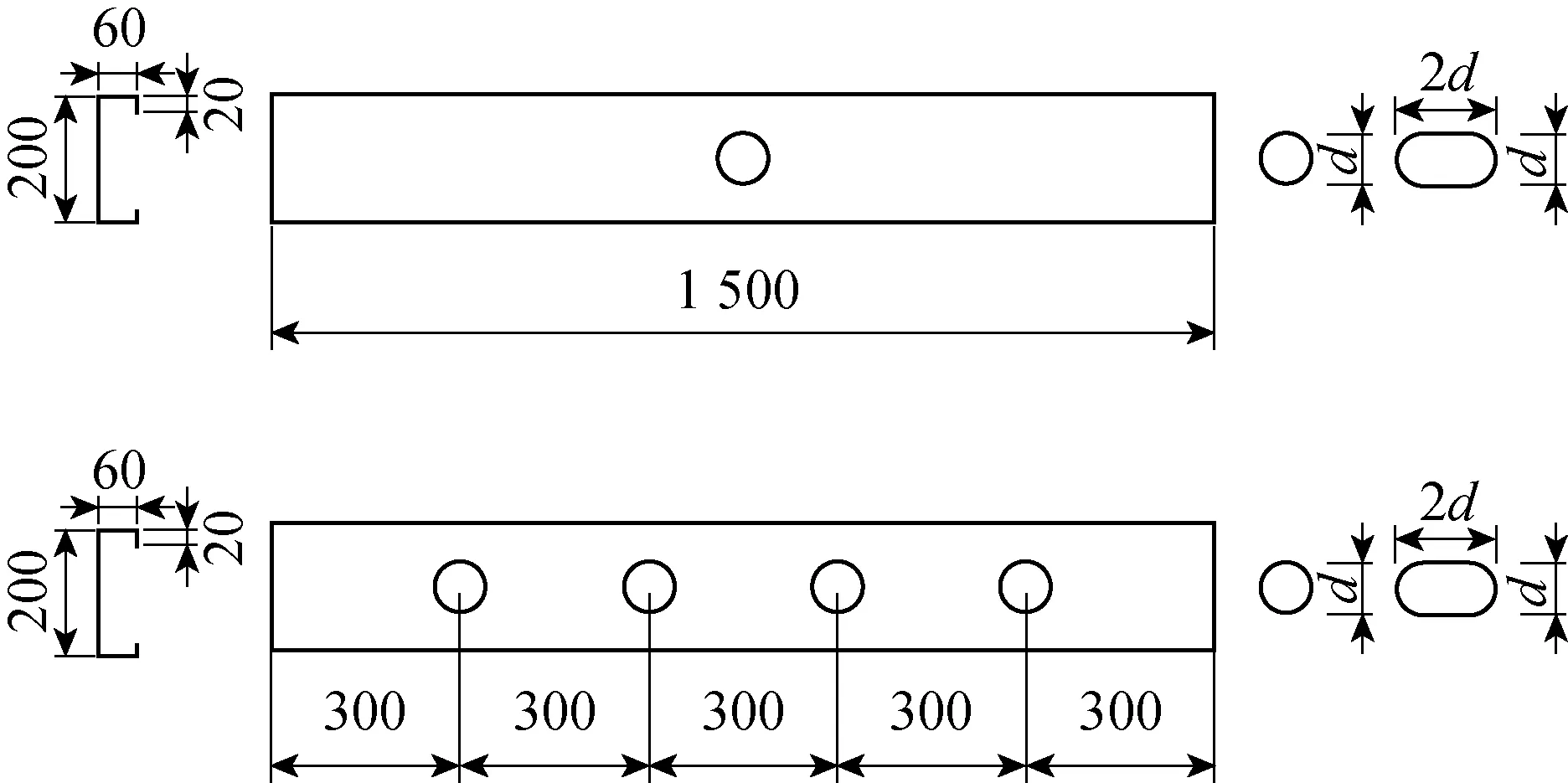
图1 构件截面和开孔形式(mm)Fig.1 Section and perforated form of a member (mm)

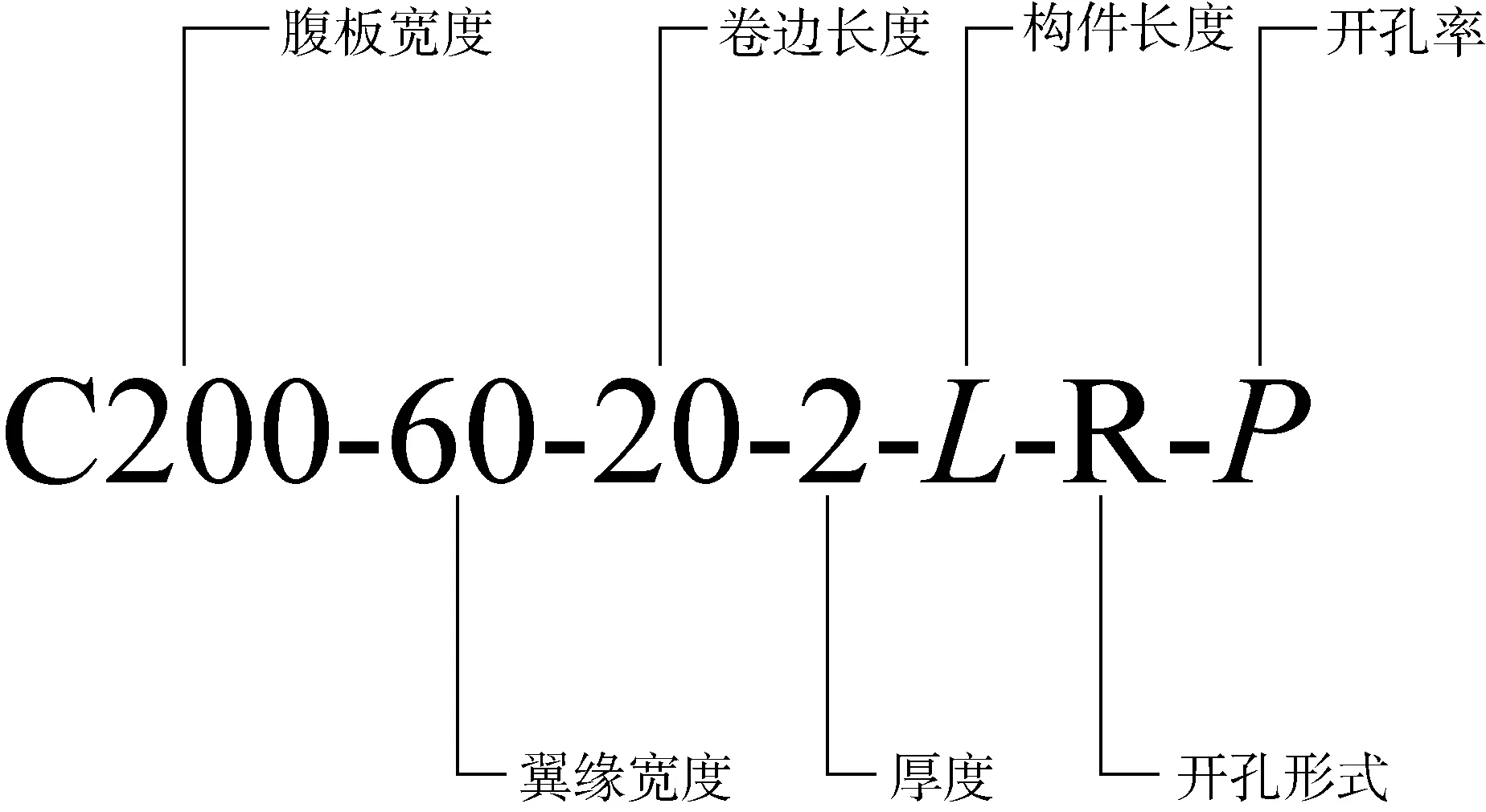
图2 构件命名规则(mm)Fig.2 Naming rule of a member (mm)

1.2 有限元模型建立

采用Abaqus 6.14-3对构件进行数值分析.弹塑性分析中，选用拉伸试验得到的Q235冷弯薄壁型钢真实应力-应变(σ-ε)关系曲线定义有限元模型中的材料，如图3所示.构件和试验方法符合GB/T 228—2010[15]规定，构件的弹性模量为2.06×105MPa，泊松比为0.3.研究对象为冷弯薄壁型钢构件，其板件厚度远小于其他方向的尺寸，故采用S4R壳单元进行建模.选取3种尺寸的网格进行计算，并最终选取了10 mm宽度的网格进行建模分析，计算结果如表1所示，Pu为极限承载力.构件腹板处有大量开孔，因此在开孔处对网格进行了更精细的划分，如图4所示.构件两端为单向铰支座，受力情况与边界条件如图5所示，U1、U2、U3为沿坐标轴方向的位移，R1、R2、R3为绕坐标轴的转动角度.数值分析分两步进行：①弹性屈曲分析，确定屈曲模态和临界载荷；②弹塑性分析，确定构件的荷载-位移曲线和极限承载力.在弹塑性分析之前，需要确定构件的初始缺陷，根据我国常用冷弯薄壁型钢构件的实测分析结果[16]，将构件的初始缺陷峰值定为构件长度的 1/1 000.

图3 应力-应变曲线Fig.3 Stress-strain curve

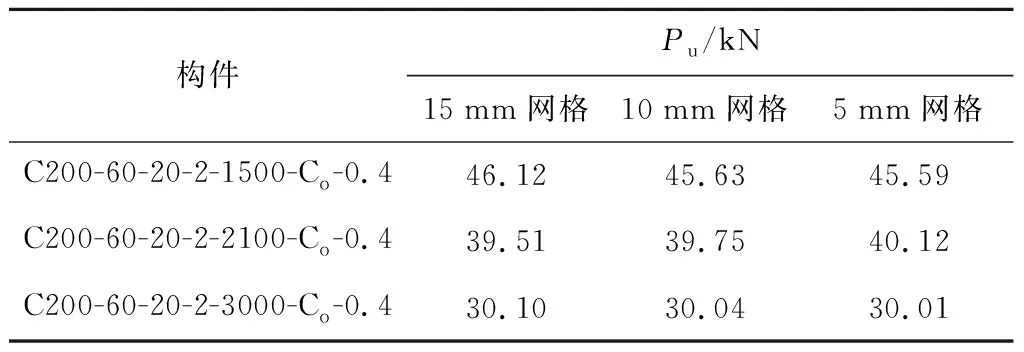
表1 网格尺寸选取Tab.1 Mesh size selection

图4 网格划分Fig.4 Mesh generation

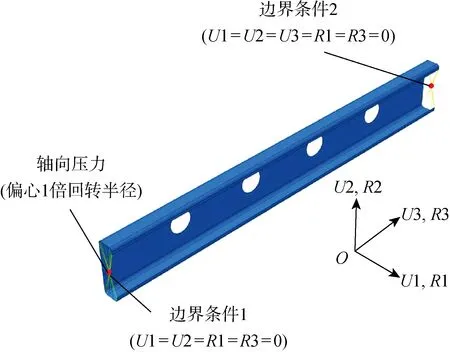
图5 边界条件Fig.5 Boundary condition

2 有限元计算结果分析

2.1 弹性屈曲分析

腹板大开孔对构件的弹性屈曲失稳模态和临界载荷有一定的影响.本文通过Young等[17]的试验结果验证了线性屈曲分析的有限元模型.图6为C200-60-20-2不同长度构件在模态数n=1～5时的屈曲临界荷载，纵坐标为临界荷载(Pcr)与屈服承载力(Py)的比值.图中对比了无孔构件、0.4和0.6开孔率连续圆孔构件(Co-0.4和Co-0.6)、0.4和0.6开孔率连续椭圆孔构件(O-0.4和O-0.6)的前5阶屈曲临界载荷，结果表明：无孔构件的屈曲临界载荷最大；同一开孔形式，大开孔率(P=0.6)构件的屈曲临界载荷小于小开孔率(P=0.4)构件的；同一开孔率，圆形开孔构件的屈曲临界载荷大于椭圆形开孔的，这是因为椭圆形开孔在沿轴向的开孔程度更大，对构件屈曲临界载荷的削弱能力更大.

表2为各长度构件前3阶的屈曲模态类型和临界载荷，其中 DB为畸变屈曲， GB为整体屈曲.图7为 1 500 mm构件的不同开孔形式和开孔率的前3阶屈曲模态变形图，从中可以看出：无孔和开孔构件的一阶屈曲模态基本一致；二阶屈曲模态虽然都是畸变屈曲，但是畸变屈曲的波形有所差异；三阶屈曲模态均呈现整体弯曲失稳，但是开孔构件的失稳模态中存在明显的畸变屈曲，即开孔构件的失稳模态是畸变-整体屈曲相关作用失稳，且随着开孔率的增加，畸变屈曲随之增加，这是由于开孔率的增加使腹板对翼缘的约束作用进一步降低.

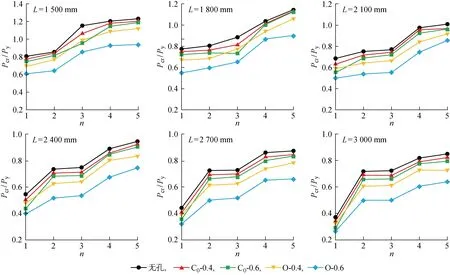
图6 开孔构件屈曲临界载荷对比Fig.6 Comparison of buckling critical loads of a perforated member

表2 屈曲模态和临界载荷Tab.2 Buckling modes and critical loads

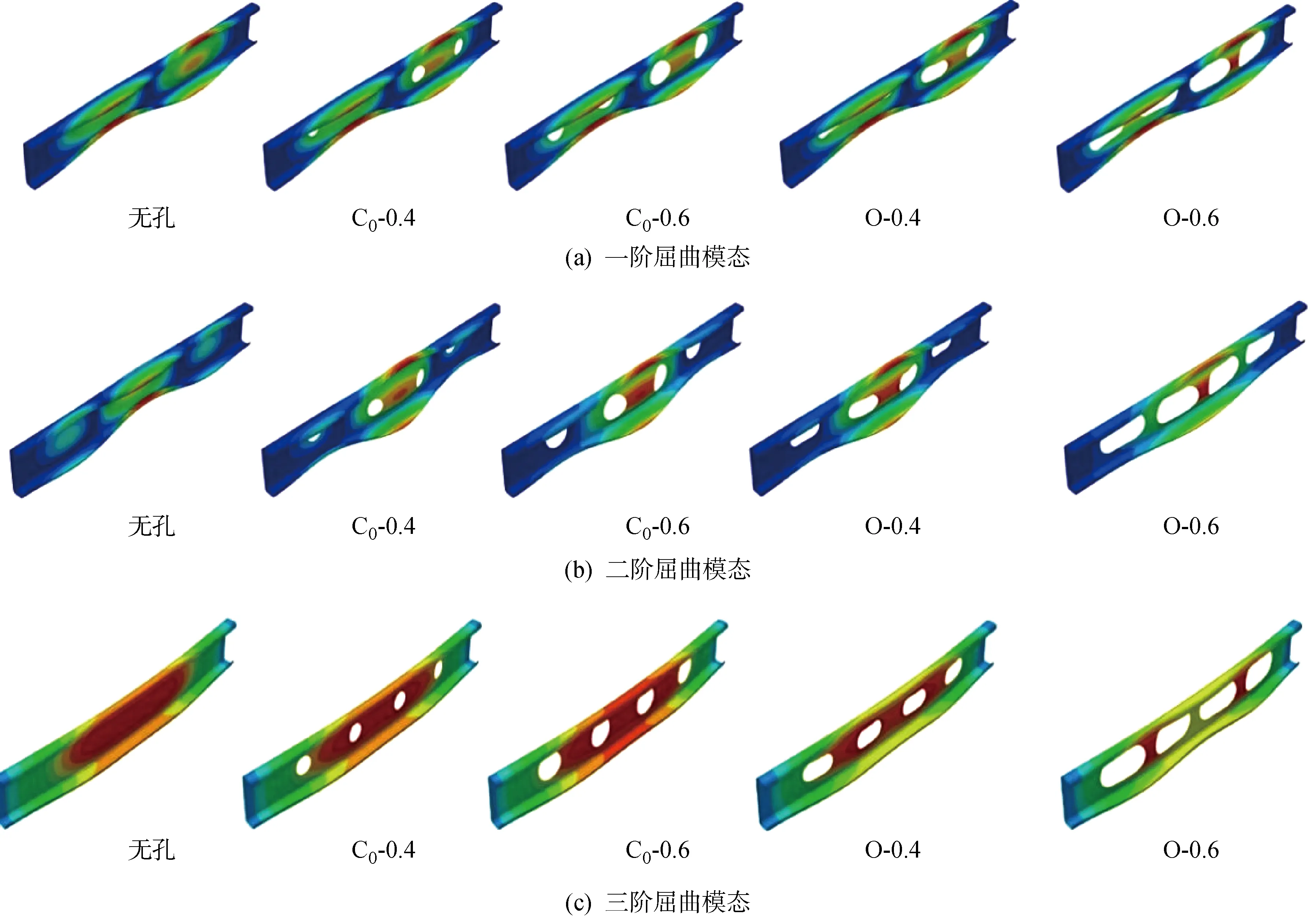
图7 屈曲模态对比Fig.7 Comparison of buckling modes

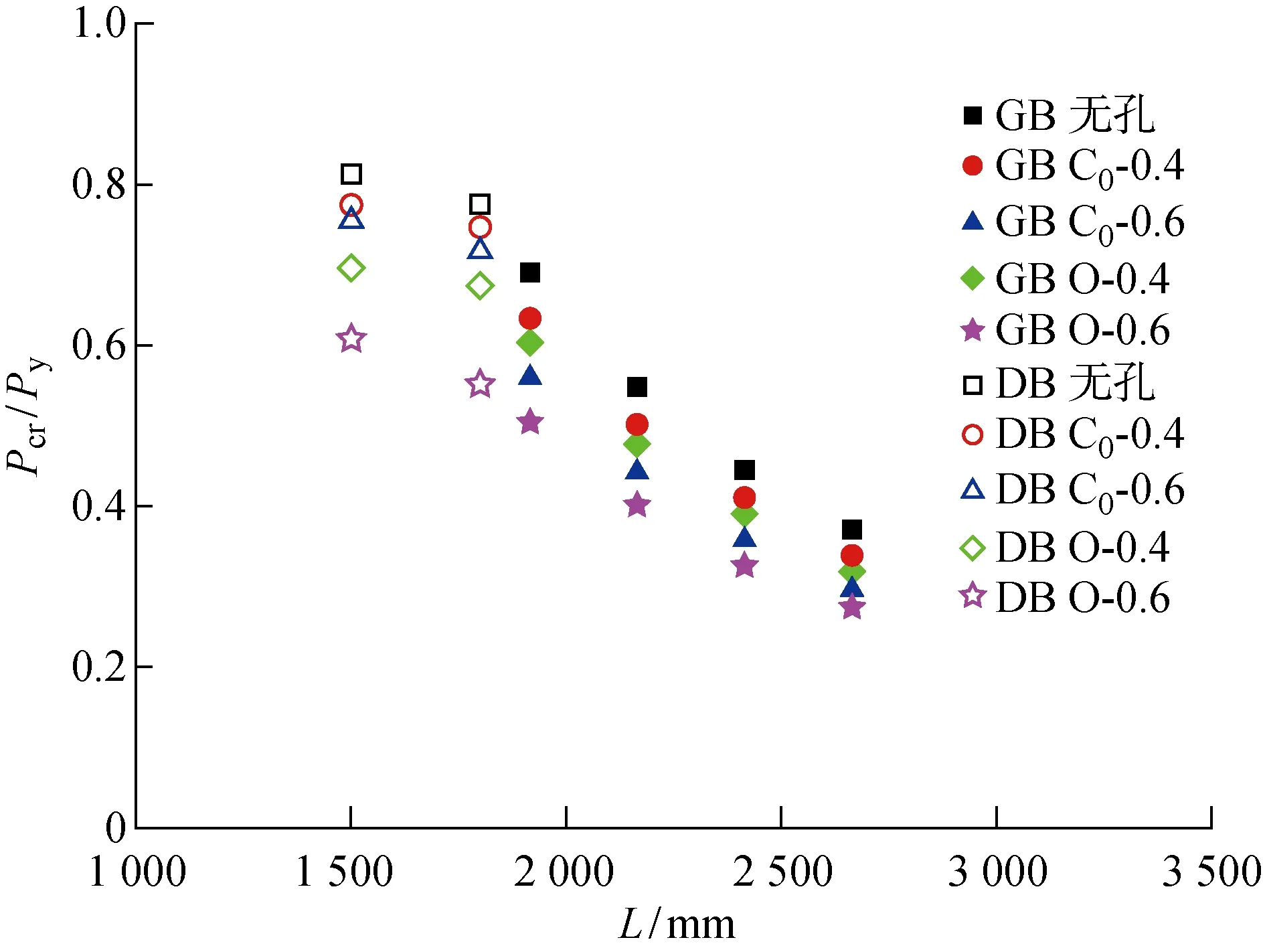
图8 不同开孔构件的临界荷载对比Fig.8 Comparison of critical loads of a member with different perforated types

为了研究开孔形式、开孔率对构件临界荷载的影响，图8对比了表2中不同开孔形式和开孔率构件的临界荷载随长度的变化情况，空心、实心图标表示一阶屈曲模态分别为畸变、整体屈曲的构件.从图中可以看出，开孔对畸变屈曲临界荷载的影响比对整体屈曲的影响大，因为整体屈曲主要受构件长度的影响，而畸变屈曲受构件长度和截面尺寸的共同影响.

2.2 弹塑性分析结果与试验结果对比

图9为3种不同长度构件的弹塑性分析与文献[18]中的构件破坏图和荷载-轴向位移(P′-D)曲线的对比关系，从图中可以看出数值模拟得到的破坏模式和试验得到的基本一致.相较于数值模拟，试验中不可控的因素较多，所以两者的荷载-轴向位移曲线略有差异，但曲线的变化趋势一致且极限荷载也比较接近.对于 1 500 mm的构件，在达到极限荷载前，构件刚度的削弱不明显，荷载位移曲线基本呈线性变化；而对于 2 100、3 000 mm的构件，在达到极限荷载的50%左右时，构件刚度明显被削弱.达到极限荷载后，3种长度的构件的承载力均下降，这是因为构件多发生畸变屈曲、畸变-整体相关屈曲或者整体屈曲破坏，畸变屈曲的屈曲后强度很小，而整体屈曲的屈曲后强度为0.表3为有限元承载力(Pu，FEA)与试验极限承载力(Pu，test)结果的对比关系，两者比值的平均值为0.91，标准差为0.03，说明有限元模型与试验结果吻合较好.

表3 有限元与试验[18]的极限承载力结果Tab.3 Ultimate loads of FEA and test[18]

2.3 开孔对极限承载力的影响

图10～12分别为不同开孔形式、开孔率和开孔位置的构件的承载力对比关系.从图10可以看出，对于小开孔率的构件，矩形孔对构件极限承载力的削弱较为显著，但总体影响并不明显；对于大开孔率的构件，开孔对构件极限承载力的削弱显著，其中矩形孔的削弱程度最大，椭圆孔其次，圆孔最小.从图11可以看出，开孔率越大，构件极限承载力的削弱越显著，且椭圆孔和矩形孔比圆孔明显，原因在于椭圆孔和矩形孔开孔率增大导致的轴向开孔尺寸增大幅度大于圆孔的.从图12可以看出，腹板跨中处开孔和腹板连续开孔都会对构件的极限承载力产生削弱作用，并且对于大多数构件，腹板连续开孔的削弱程度更大.

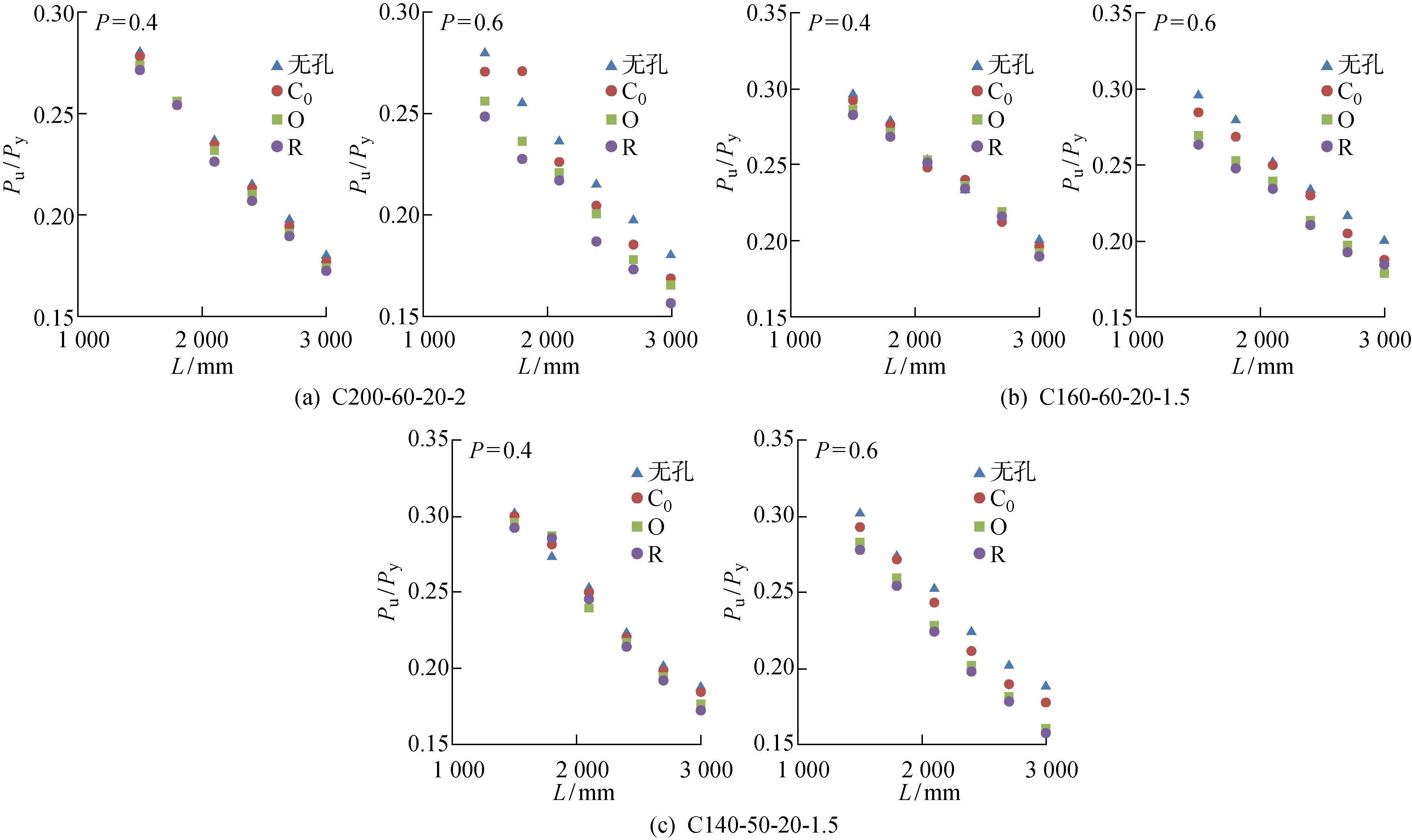
图10 不同开孔形式构件的承载力对比Fig.10 Comparison of bearing capacities of a member with different perforated types

图11 不同开孔率构件承载力对比Fig.11 Comparison of bearing capacities of a member with different perforated ratios

图12 不同开孔位置的构件承载力对比Fig.12 Comparison of bearing capacities of a member with different perforated positions

3 DSM计算立柱承载力

DSM是由Schafer和Peköz于1998年首次提出并用以计算冷弯薄壁型钢结构构件的承载力，Schafer在后续的研究中提出了无孔冷弯薄壁轴压构件的DSM计算公式[19].随着立柱开孔形式日益多样化，上述DSM公式无法满足冷弯薄壁型钢开孔轴压立柱的承载力计算，因此Moen等[20]对现有无孔压杆DSM公式进行了修正，提出了腹板开孔槽钢构件的DSM计算公式，但并不适用于本文研究的冷弯薄壁型钢压弯构件.本文基于文献[21]中提出的偏心受压卷边槽钢构件的稳定承载力DSM公式建立过程，利用数值模拟得到的极限承载力结果，建立冷弯薄壁型钢开孔压弯立柱的DSM公式.从数值模拟结果可以看出，中长构件多产生畸变-整体屈曲相关作用失稳破坏，因此需要对冷弯薄壁型钢开孔压弯构件DSM畸变屈曲设计公式进行修正.修正后用于开孔C型钢压弯构件的畸变-整体相关屈曲极限承载力系数为

(1)

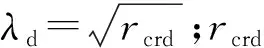
(2)

(3)

式中：Mon为偏压构件极限弯矩；e为荷载偏心距；Mynet为净截面屈服弯矩.上述直接强度法公式中为开孔构件的屈曲临界载荷，屈服荷载和弯矩均考虑了开孔的影响.

采用上述修正公式得出的开孔压弯构件畸变-整体相关屈曲DSM曲线如图13所示，修正后的曲线与数值模拟结果较吻合.另外，图中对比了无孔轴压立柱畸变屈曲、开孔轴压立柱[19]、修正后用于压弯构件畸变相关屈曲的DSM曲线和数值模拟结果.结果表明，无孔和开孔轴压立柱DSM曲线均不适用于本文研究的开孔C型压弯构件；修正后的DSM曲线能够有效预测孔间距为300 mm，开孔率为0.4和0.6的冷弯薄壁C型绕强轴的单向压弯构件的极限承载力.

图13 开孔压弯构件畸变-整体相关屈曲DSM曲线Fig.13 DSM curves of perforated member under combined compression and bending

4 结论

对180根不同开孔形式、开孔位置、开孔率和长度的冷弯薄壁C型钢压弯构件进行有限元弹性和弹塑性数值分析，对其屈曲临界荷载、屈曲模态、极限承载力及其相应的破坏模式进行研究.数值分析结果与已有试验数据进行校对，验证了数值模型的可靠性.基于数值模拟结果，对现有无孔冷弯薄壁型钢轴压构件的DSM公式进行修正.具体结论如下：

(1) 开孔会影响构件的临界荷载，开孔形式、位置和开孔率对构件的低阶屈曲模态无影响，但是对畸变屈曲波数和同阶屈曲模态中不同屈曲模态所占比例有影响.

(2) 开孔构件的承载力低于无孔构件的.其中，矩形孔、椭圆孔的降低幅度比圆孔的大；腹板连续开孔构件的承载力低于腹板跨中单一开孔的低于无孔构件的；大开孔率构件的承载力低于小开孔率的.

(3) 基于DSM理论和参数分析结果，提出了适用于开孔冷弯薄壁型钢C型压弯构件的承载力计算公式.