面向基因表达数据聚类的谱扰动集成降维
庄姗姗,陈晓云
(福州大学 数学与计算机科学学院,福建 福州 350108)
0 引 言
基因表达数据高维小样本的特点,易产生维数灾难问题,从而降低聚类算法的性能[1]。因此,针对基因表达数据聚类的降维方法进行研究是有重要意义的。现有降维方法大多直接对基因表达数据进行一次降维,再利用降维后的数据进行聚类,未考虑降维和聚类之间的联系,降维后的数据未必能很好地适应聚类任务。
集成学习可提高模型的泛化能力,但较少将集成学习思想应用于降维模型中。而基于加权的集成学习模型,常见的加权策略有两种。一是由人为控制参数权重,比如平均加权[2];二是将集成的全部数据集函数目标值最小化[3],即目标值越小的数据集的权重越大,但是,目标值越小的数据集,其模型的聚类性能不一定越好。
综上所述,本文将集成学习思想和基于聚类能力的加权方法用于降维模型中,对高维基因表达数据抽取特征组合生成多个样本子集,每个新样本子集进行降维,根据谱扰动理论基于聚类能力学习获得权重,加权组合得到最终降维结果,该方法将集成思想和谱扰动加权用于降维模型,对特征多次学习充分利用高维特征,基于聚类能力加权组合多个降维结果,使得最终降维结果能够更好地适应聚类任务。
1 相关工作
1.1 投影降维方法
为解决维数灾难问题,许多研究假设高维观测数据在其环绕空间中具有低维结构,旨在寻找一投影将高维空间降维到低维子空间中[4]。
局部保持投影(LPP)意在维持投影前后样本间的近邻关系一致,是一种基于谱图理论的降维方法[5]。LPP运用k近邻的关系来构造样本间的权图,假设数据集X∈RD×n,有n个样本和D个特征,如下定义相似矩阵Z
(1)
其中,Nk(xi)是xi的k近邻组成的集合。LPP的目标函数为
(2)

基于最小二乘优化的低秩投影(LPLSR)[6]将观测数据矩阵X∈RD×n分为两部分X=Y+E,其中Y是真实数据,E是噪声项,利用低秩方法将真实数据Y投影到潜在低维子空间中。LPLSR的目标函数为
(3)

1.2 谱扰动
Laplacians矩阵中元素任何微小的变化都会导致特征向量巨大的变化。谱聚类的聚类结果依赖于Laplacians矩阵的前k个特征向量,故可用一组特征向量的聚类表现来衡量聚类能力。如果聚类能力差异越小的两组特征向量,它们之间的聚类结果就越相近。两组特征向量之间聚类能力的差异采用欧式距离衡量,会出现两特征向量组欧式距离大但聚类能力相近的情况,进一步可用两组特征向量之间的划分特征空间的规范角来衡量聚类能力的差异。因此,可基于谱扰动理论用两组特征空间的最大规范角来衡量聚类结果之间的差异。

θj=arccosγj
(4)

2 本文方法
2.1 集成降维

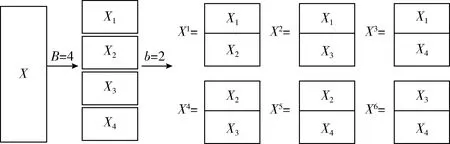
图1 模块的划分组合
对c个新样本子集X1,…,Xc应用文献[6]中基于最小二乘优化的低秩投影(LPLSR)进行降维
(5)
其中,Pa、Za和Ea分别为样本子集Xa的低秩投影矩阵、相似矩阵和噪声项。每个样本子集Xa降维后的数据为Ya=PaTXa,集成降维为
(6)
其中,μa是降维后样本子集Xa的权重。降维过程中应用集成学习思想,对特征多次学习,加权组合多个降维结果,充分利用基因表达数据的高维特征。
权重μ=[μ1,…,μc]不同的定义得到不同的模型:可根据降维后每个子集的误差为权获取权重,误差越小的数据子集其权重越大,得到EM-IDR
(7)
然而,目标值越小的数据子集,所对应模型的聚类效果不一定越好。也有直接人为定义权重的,大多采用平均加权,即A-IDR
μa=1/c,a∈{1,…,c}
(8)
但是每个样本子集Xa的数据不同,降维后的数据对最终的聚类结果的影响不尽相同。
综上分析,本文进一步改进加权方法,基于谱扰动理论衡量聚类能力来学习权重μ,可用一组特征向量即Laplacians矩阵的前k个特征向量来衡量聚类能力,用两组特征向量之间的划分特征空间的规范角来衡量聚类能力的差异。理想情况下,由于样本子集X1,…,Xc的每个样本都源于同一原始样本,每个样本子集的聚类结果应该和一致的聚类结果相同,因而每个样本子集真实的相似矩阵应该是相同的,即所有样本子集之间存在一个相同的真实的Laplacians矩阵。然而在一般情况下,真实的Laplacians矩阵是未知的,通过μ加权组合每个样本子集的Laplacians矩阵获得一致Laplacians矩阵
(9)

本文基于两个原则学习权重μ:一是将一致聚类结果与每个子集聚类结果的差异最小化原则,二是聚类能力相近的样本子集应有近似权重原则,通过样本子集间的聚类能力更好地集成降维,使降维后的数据更适用于聚类任务。
2.2 加权策略


(10)


(11)
原则二:聚类能力相近的样本子集应有近似权重。如上所述,根据谱扰动理论,两样本子集间的聚类能力越相似,特征空间中的最大规范角越小,权重越相近。令Cab∈[0,π]为Xa与Xb间的最大规范角,Rab=π-Cab,则有
(12)

最后,将式(11)和式(12)相结合,得到最终谱扰动加权目标函数
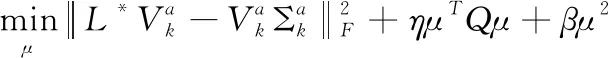
(13)
其中,式(13)中最后一项为正则项。保证每个样本子集Xa降维后的数据Ya都对最终降维结果Y有贡献,η和β均为平衡参数。
式(13)去掉与μ无关项,可得
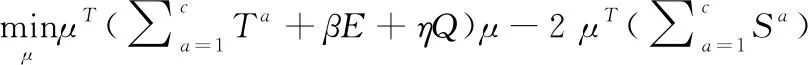
(14)

式(14)是标准的二次规划问题,可用Matlab的quadprog求解μ。
2.3 谱扰动集成降维算法
算法:谱扰动集成降维算法(SD-IDR)
输入:数据矩阵X,参数λ、η、β,样本划分数B,组合数b
输出:降维后的样本矩阵Y

步骤2 根据式(5)求解X1,X2,…,Xc的投影矩阵P1,P2,…,Pc与相似矩阵Z1,Z2,…,Zc;
步骤3 根据式(14)求解μ;
步骤4 根据式(6)计算降维后的样本矩阵。
SD-IDR算法的时间复杂度主要有两方面:
一是求解投影矩阵和相似矩阵,该时间复杂度同LPLSR的时间复杂度相同,即为O(n3+n2d),由于基因表达数据中d>>n,故时间复杂度为O(n2d)。二是求解权重,该过程主要在于计算Ta、Sa和Q,时间复杂度为O(c3n2)。
综上所述,最终SD-IDR算法的时间复杂度为O(c3n2+n2d)。
3 实 验
实验选用6个公开应用较为广泛的基因表达数据集[8,9]:Leukemia0,Leukemia1,Leukemia2,Lung_Can-cer,DLBCL和Lymphoma,信息整理见表1。
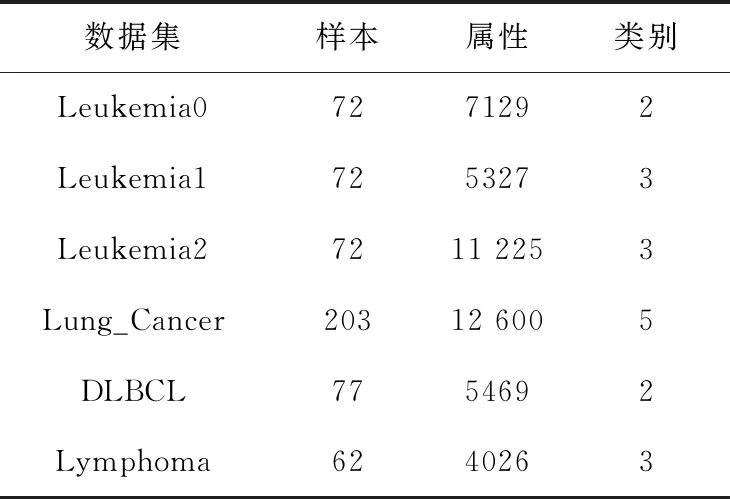
表1 数据集描述
3.1 实验设置

3.2 实验结果与分析
本文对降维后样本采用K-means聚类,降维质量以聚类准确率ACC来衡量。选用3种集成加权降维方法:EM-IDR、A-IDR和S-ELM[3],4种非集成降维方法:LPLSR[6]、URAFS[10]、SOGFS[11]和JELSR[12],与本文SD-IDR方法对比。所有方法的平衡参数也均在[10-3,10-2,…,102,103]中遍历取优,为尽可能避免随机性的因素,所有方法都运行10次取均值。
由表2可见,谱扰动集成降维SD-IDR在所有数据集下的聚类准确率最高。对比LPLSR、URAFS、SOGFS和JELSR单一降维方法,SD-IDR方法的聚类效果更为理想,这表明将集成学习思想用于降维模型,对特征进行多次学习,能够充分利用基因表达数据的高维特征,提高聚类准确率。对比EM-IDR、A-IDR和S-ELM集成降维方法,SD-IDR基于聚类能力的集成降维方法的聚类效果更为理想,这表明本文利用谱扰动理论的加权集成方法通过聚类能力更好地指导降维,使得最终降维后的样本能够更好地适应聚类任务。

表2 聚类准确率对比/%
4 结束语
本文将集成学习思想和基于聚类能力的加权方法用于降维模型中,对高维数据抽取特征组合生成多个样本子集,每个新样本子集进行降维,根据谱扰动理论基于两个原则:一致聚类结果与每个子集聚类结果差异最小化原则和聚类能力相近的样本子集应有近似权重原则,学习获得权重μ,加权组合得到最终降维结果。该方法将集成思想和谱扰动加权用于降维模型中,对特征多次学习,充分利用高维特征,利用聚类能力加权组合多个降维结果,通过聚类能力更好地集成降维,使得降维能够更好地适应聚类任务。

