斜拉桥液体粘滞阻尼器参数敏感性分析
王志伟,李春良
吉林建筑大学 交通科学与工程学院,长春 130118
0 引言
大跨度斜拉桥在设计之初,通常选用隔震体系设计,使结构变得更柔,却会使结构产生过大的位移,容易导致主梁碰撞、支座剪切破坏等灾害[1].国内外的大跨度桥梁多采用消能减震设计来满足地震动设防性能目标,被动消能减震技术通过对结构设置附加阻尼器装置来耗散地震能量,可以显著改善桥梁地震作用下的响应[2].由于地震动的空间性、随机性以及大跨度斜拉桥的非线性特性等诸多因素,使得大跨度斜拉桥的动力响应分析格外复杂,故本文以大跨度斜拉桥为工程背景,基于结构的地震响应控制原理,系统的分析了结构附加粘滞液体阻尼器后的动力响应以及粘滞液体阻尼器减震效果.
1 液体粘滞阻尼器
液体粘滞阻尼器阻尼力与速度指数的关系为:
F=CVα
(1)
式中,F为阻尼力,kN;C为阻尼系数,kN·(s·m-1)α;V为阻尼器相对速度,m/s;α为速度指数.液体粘滞阻尼器的减震效果主要依赖于α,C二者的取值,其中速度指数α应用于地震作用下时通常取0.3~1[3].
根据厂家提供的液体粘滞阻尼器实验数据表明,液体粘滞阻尼器的滞回曲线较为饱满,如图1滞回曲线所示:当液体粘滞阻尼器速度指数α逐渐增大时,滞回曲线面积由矩形逐渐减小为椭圆,当液体粘滞阻尼器速度指数α=1时,滞回曲线面积最小,说明其滞回耗能能力逐渐降低.如图2 液体粘滞阻尼器的力与速度关系所示:当速度指数α=1时,阻尼器为线性阻尼器,0<α<1时,阻尼器为非线性阻尼器[4-6].
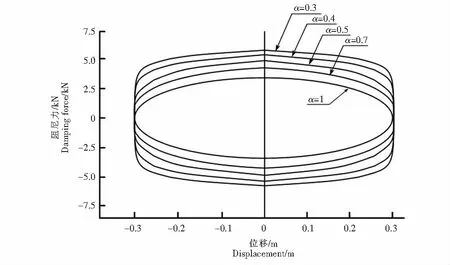
图1 滞回曲线Fig.1 Hysteresis curves
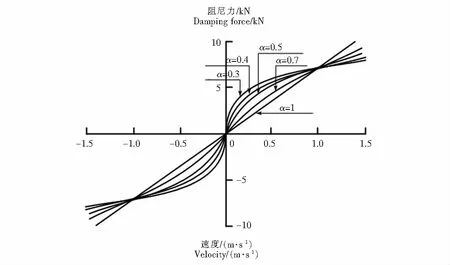
图2 力-速度曲线Fig.2 Force-speed curves
2 液体粘滞阻尼器参数敏感分析
2.1 算例
以双塔双索面组合梁斜拉桥为研究对象,总体布置如图3所示.采用梁、塔分离的半漂浮体系的结构形式.主梁采用钢-混凝土组合梁,由钢梁和桥面板组成,主桥桥址位于Ⅵ度地震区.
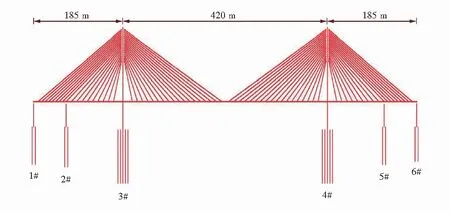
图3 总体布置Fig.3 Overall layout
建立有限元动力分析模型,有限元模型如图4所示,计算将实际斜拉桥进行结构离散,全桥共划分节点4 413个,单元4 544个.利用有限元软件中的只受拉桁架单元来模拟模型中的拉索,空间梁单元来模拟模型的横梁、塔、纵梁、墩以及桩基础.主梁节点和斜拉索吊点采用主从连接.承台底部采用六弹簧考虑群桩基础.液体粘滞阻尼器采用内力型粘弹性消能器Maxwell模型模拟.
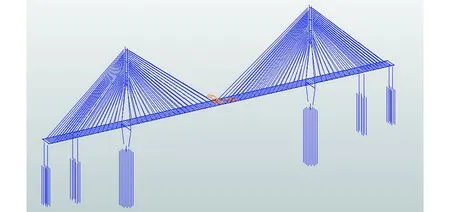
图4 有限元模型Fig.4 Finite element model
2.2 地震动输入
选取3条100年超越概率3%的地震波(罕遇地震)按照纵向+竖向输组合进行非线性时程分析.设计反应谱最大值Smax依据式(2)~式(3)求得设计加速度峰值(PGA),进行幅值调整,图5为一调幅过的罕遇地震时程曲线,根据《公路桥梁抗震设计细则》(JTGTB 02-01-2008),本文采用三组计算结果中的关键部位响应最大值来衡量.
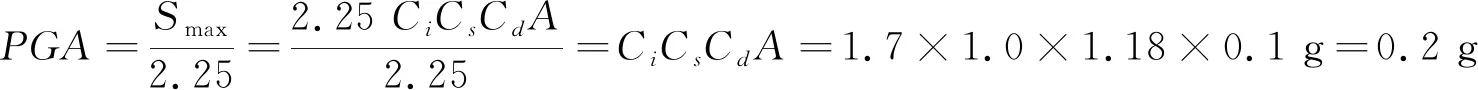
(2)
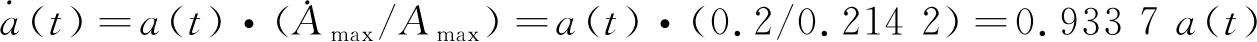
(3)
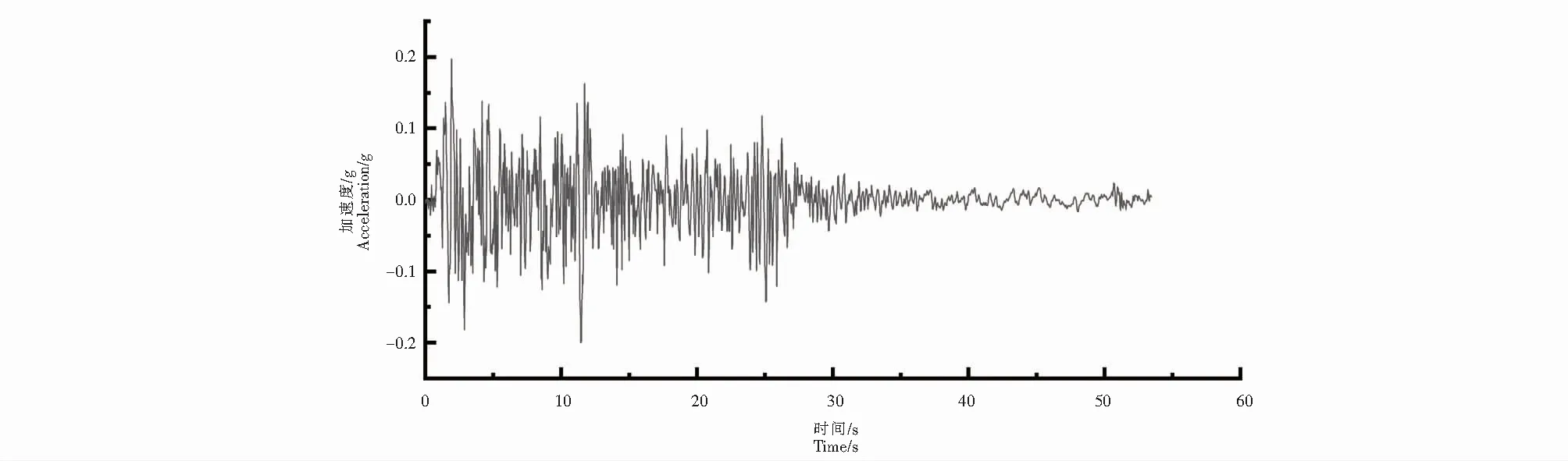
图5 1940年埃尔森特罗(El-Centro)地震波加速度反应谱曲线Fig.5 1940 El-Centro seismic wave acceleration response spectrum curve
2.3 液体粘滞阻尼器力学参数敏感性分析
在附加液体粘滞阻尼器进行斜拉桥减隔震设计时,合理设置液体粘滞阻尼器敏感参数对阻尼器减震效果尤为重要.根据现有工程经验,液体粘滞阻尼器通常布置在主塔下横梁与主梁连接处,本文模型中每个桥塔设置2个液体粘滞阻尼器,共4个液体粘滞进行减隔震设计[7].为讨论阻尼器力学参数对结构减震性能的影响,分别取α=0.3,0.4,0.5,0.7,1;C=1 000 kN·s/m,2 000 kN·s/m,3 000 kN·s/m,4 000 kN·s/m,5 000 kN·s/m,针对25种不同阻尼器参数工况,进行非线性时程分析,具体计算结果如图6~图11所示.
(1) 位移效应
图6、图7分别为对比结构未设置液体粘滞阻尼器,设置阻尼器不同敏感参数工况时的3#与4#塔顶、梁端与主跨跨中等控制处的纵向位移变化规律图.由图6(3#,4#塔顶纵向位移)可知,在设置的25组液体粘滞阻尼器敏感参数工况中,3#,4#塔顶纵向位移变化规律:在速度指数α不变时,随阻尼系数C增大,3#,4#塔顶纵向位移减小,但随阻尼系数C的不断增大,位移曲线斜率趋于平缓甚至出现拐点呈上升趋势,阻尼器减震效果降低;在阻尼系数C不变时,随速度指数α减小,3#、4#塔顶纵向位移总体呈递减趋势,且阻尼系数越小,减小趋势越明显.由图7(梁端与主跨跨中纵向位移)可知,在设置的25组液体粘滞阻尼器敏感参数工况中,梁端、主跨跨中纵向位移变化规律:在速度指数α不变时,梁端、主跨跨中纵向位移随阻尼系数C成反比,随阻尼系数的增大,位移曲线斜率趋于平缓,阻尼器减震效果逐渐降低.在阻尼系数C不变时,随速度指数α减小,梁端以及主跨跨中纵向位移递减,且阻尼系数越小,减小趋势越明显.
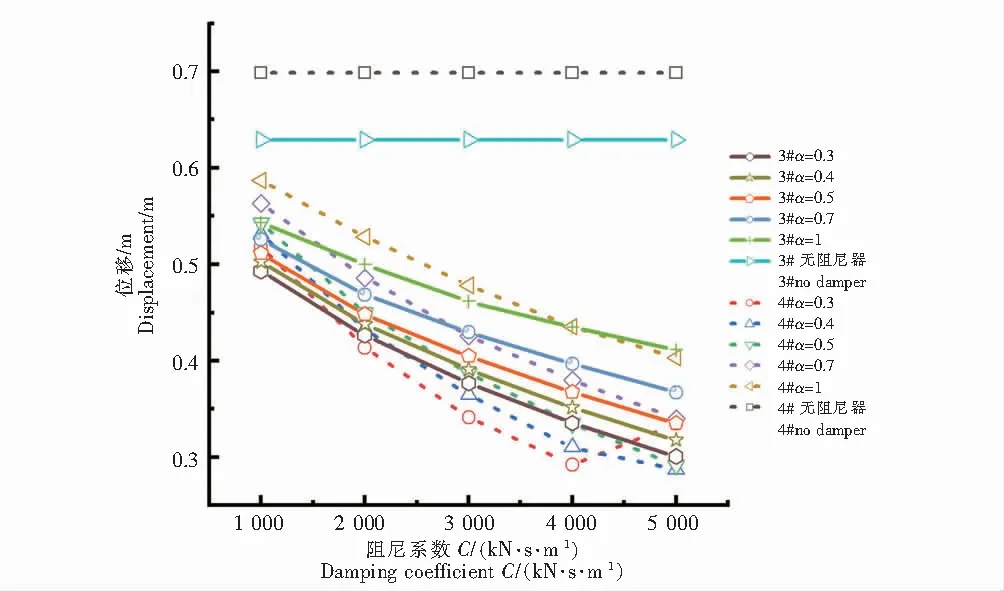
图6 3#、4#塔顶纵向位移Fig.6 Longitudinal displacement of 3#、4#tower top
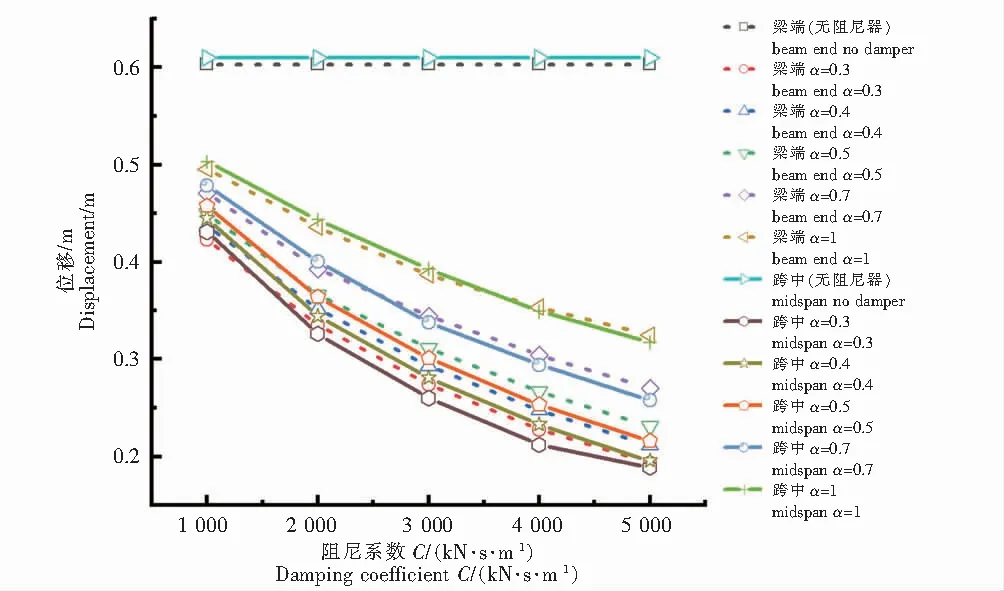
图7 梁端与主跨跨中纵向位移Fig.7 Longitudinal displacement of beam end and main span
(2) 内力效应
图8、图9分别为结构附加不同敏感工况的液体粘滞阻尼器后,结构相较于未设置液体粘滞阻尼器时控制部位4#塔底的剪力与弯矩变化规律图.由图8(4#塔底剪力)可知,在设置的25组液体粘滞阻尼器敏感参数工况中,控制部位4#塔底的剪力变化规律:在速度指数α不变时,4#塔底剪力随着阻尼系数C的增大,剪力值总体上呈下降趋势,但随阻尼系数C的继续增大,剪力曲线斜率变平缓,减小程度较小,减震效果差异不大;在阻尼系数C不变时,4#塔底剪力随速度指数α的增大,总体上呈上升趋势.通过图9(4#塔底弯矩)可知,在设置的25组液体粘滞阻尼器敏感参数工况中,控制部位4#塔底的弯矩变化规律:在速度指数α不变时,4#塔底弯矩在阻尼系数增大时,弯矩值也随之减小,但随阻尼系数C的继续增大,弯矩曲线斜率变平缓,减小程度较小,速度指数越小越明显;在阻尼系数C不变时,4#塔底弯矩在速度指数α增大时,弯矩值增大,且随速度指数增加越明显.
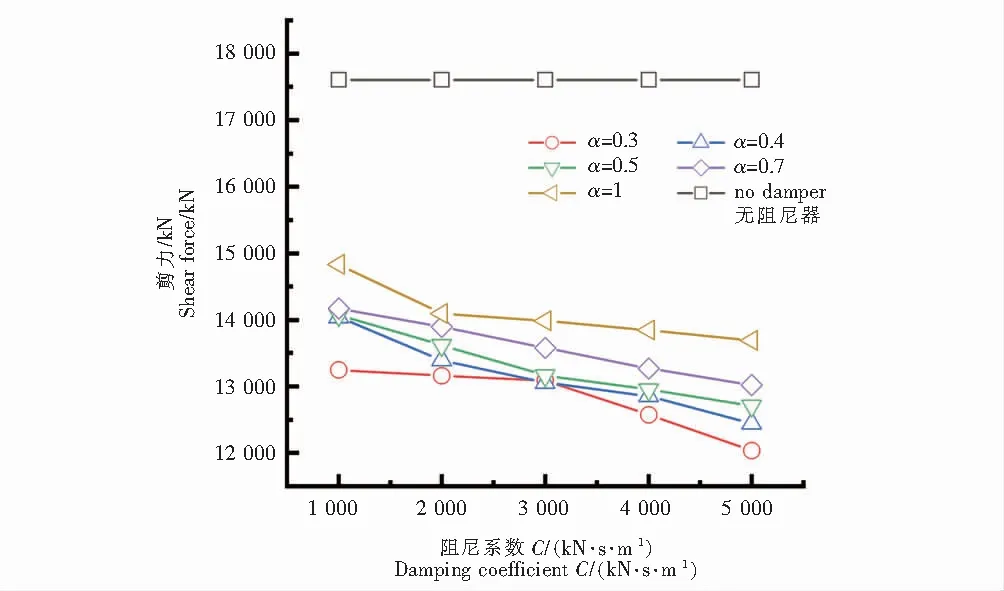
图8 4#塔底剪力Fig.8 4# bottom shear
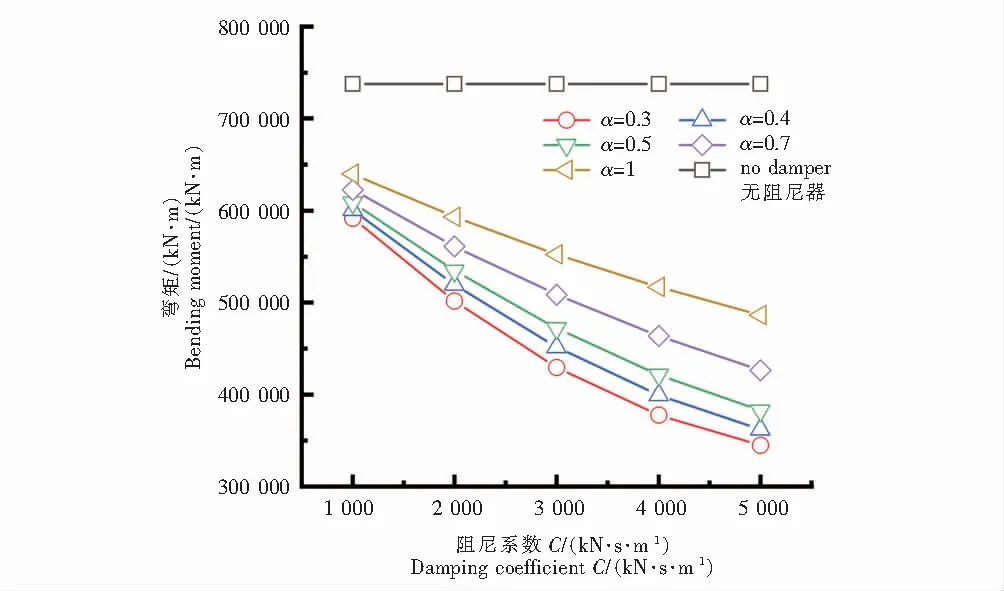
图9 4#塔底弯矩Fig.9 4# bottom bending moment
(3) 阻尼器性能
图10、图11分别为液体粘滞阻尼器设置不同敏感参数工况,4#桥塔粘滞液体阻尼器行程、阻尼力的变化规律图.通过图10(4#阻尼器行程)可知,在设置的25组液体粘滞阻尼器敏感参数工况中,布置在4#塔梁处的液体粘滞阻尼器行程规律:在速度指数α不变时,阻尼系数C减小,液体粘滞阻尼器的最大行程递增.本文选取的4#塔梁处的液体粘滞阻尼器最大行程范围为0.28 m~0.45 m.通过图11(4#阻尼器阻尼力)可知,在设置的25组液体粘滞阻尼器敏感参数工况中,布置在4#塔梁处的液体粘滞阻尼器阻尼力规律:在速度指数α不变时,阻尼系数C减小,液体粘滞阻尼器的阻尼力递减.
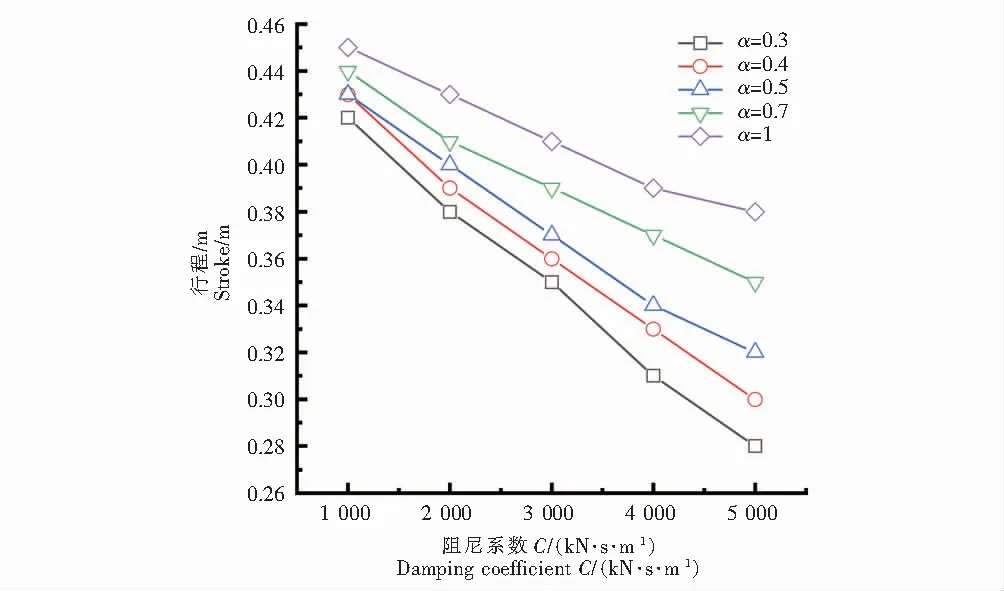
图10 4#阻尼器行程Fig.10 4# damper stroke
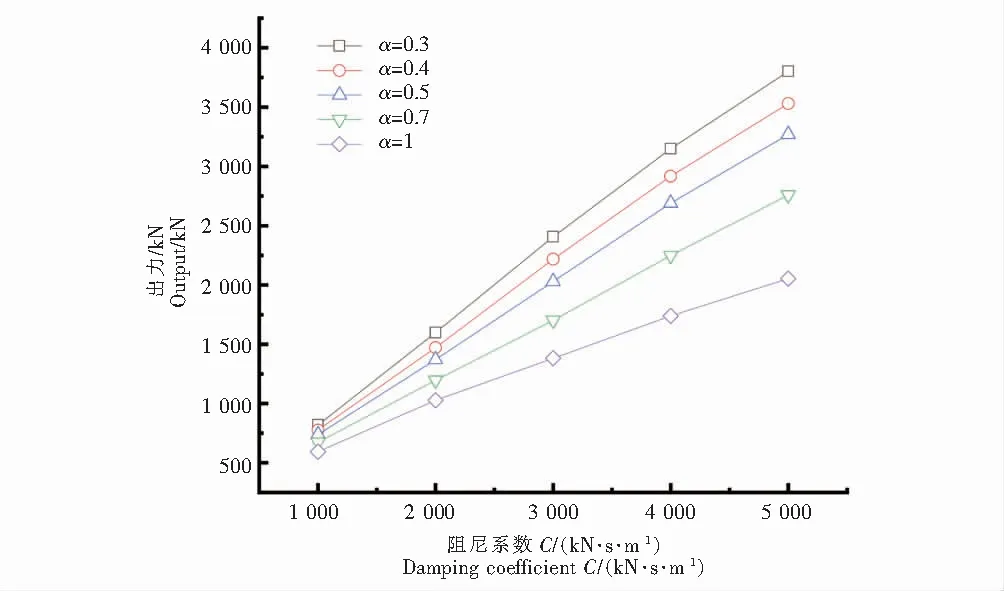
图11 4#阻尼器阻尼力Fig.11 4# damping force of the damper
3 减震效果分析
为研究附加液体粘滞阻尼器对大跨径斜拉桥减震控制效果,在E 2等级地震作用下,对无控与有控模型输入100年超越概率3 %的地震波,对比控制部位的位移以及内力值,根据上文不同阻尼系数与速度指数工况下的结构响应规律,将粘滞液体阻尼器的25组参数工况带入计算,综合考虑结构位移、内力以及阻尼器行程和阻尼力等因素,经计算得到当工况C=5 000 kN·s/m,α=0.3时,阻尼器减震效果最优,相应的时程曲线如图12~图14所示.
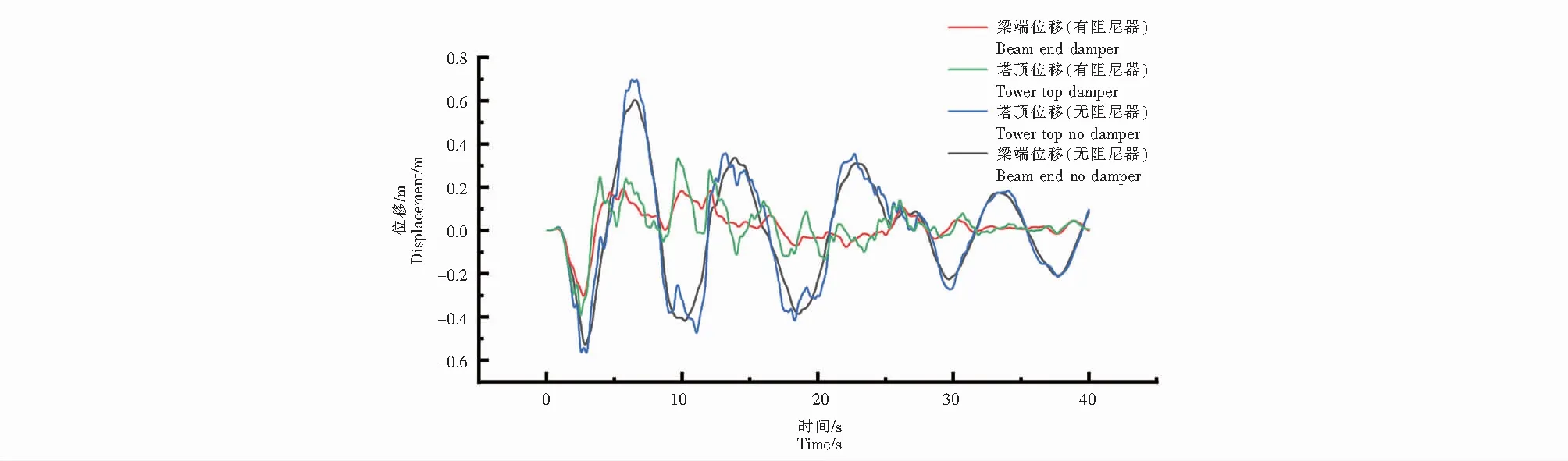
图12 梁端与4#塔顶位移时程曲线Fig.12 Beam end and 4# tower top displacement time history curve
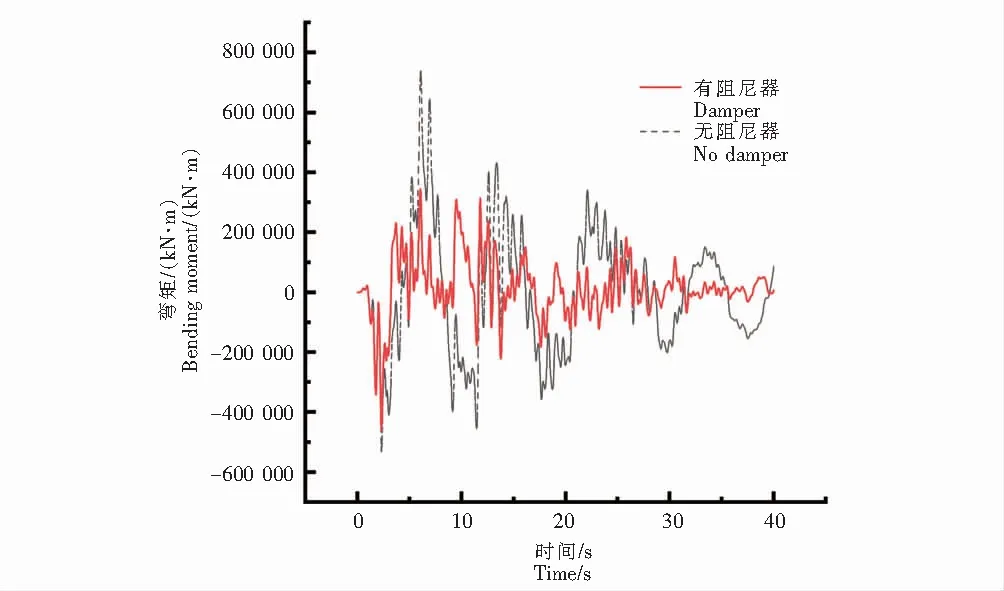
图13 4#塔底弯矩时程曲线Fig.13 Bending moment time history curve of 4# tower bottom
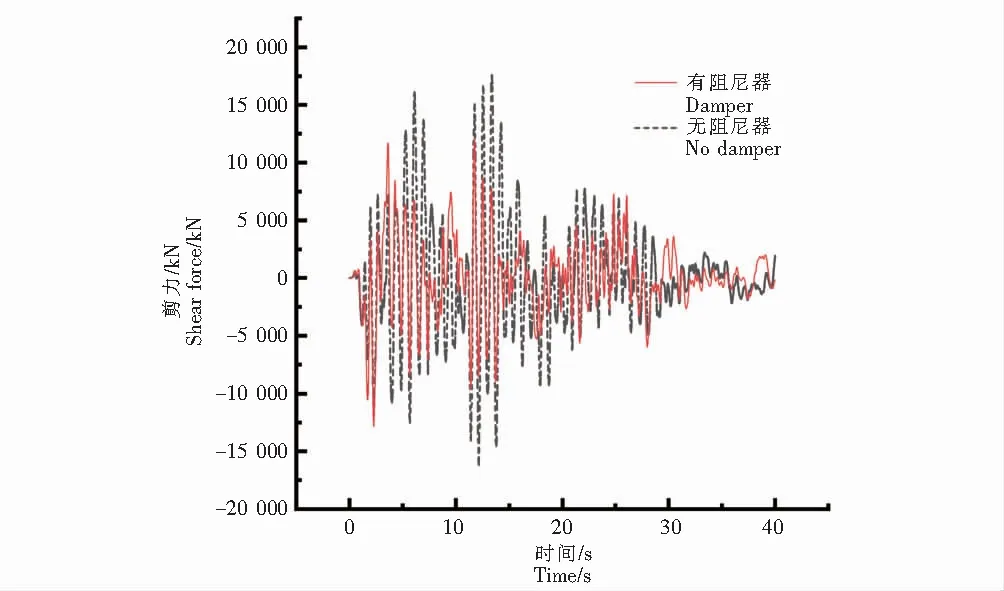
图14 4#塔底剪力时程曲线Fig.14 Shear time history curve of 4# tower bottom
由图12(梁端与4#塔顶位移时程曲线)可知,对比未设置阻尼器,结构在附加合理参数粘滞液体阻尼器后,梁端与4#塔顶位移明显减小,由图13(4#塔顶弯矩时程曲线)、图14(4#塔顶剪力时程曲线)可知,对比未设置阻尼器,在斜拉桥附加合理参数粘滞液体阻尼器后,4#塔底弯矩值、剪力值明显减小.通过图12~图14可知,结构各控制值相较于原结构均有着不同程度的减小,斜拉桥在附加合理敏感参数工况的液体粘滞阻尼器有着良好的减震作用.
4 结论
(1) 对比未设置粘滞液体阻尼器的结构,在塔-梁纵向设置合理敏感参数工况的液体粘滞阻尼器能有效地降低结构关键部位的位移及塔底内力.
(2) 在合理敏感参数取值范围内,当液体粘滞阻尼器速度指数α一定时,随着阻尼系数C的增大,梁端、塔顶等结构关键部位的位移和阻尼器行程随之减小;塔底内力基本上呈下降趋势,且速度指数α越小,下降趋势越显著,液体粘滞阻尼器减震效果越好.
(3) 在本文设置的25组液体粘滞阻尼器敏感参数工况中,经计算可知,当液体粘滞阻尼器阻尼系数C=5 000 kN·s/m、速度指数α=0.3时,液体粘滞阻尼器对结构有较好的减震效果.

