基于点云数据与钻孔数据的土石方计算

温成龙

(中煤天津设计工程有限责任公司，天津 300131)

土方和石方的计算涉及露天矿开采、土地整治、工程建设等众多领域[1]，土方挖方单价与石方挖方单价相差2～5倍[2]，土方和石方计算的准确度对工程投资产生直接影响。目前，由于土石方工程在大部分工程项目总投资中所占比例较小[3]，实际工作中很少对土方量和石方量分别进行计算。土方量和石方量的准确计算对控制工程预算和优化设计方案具有重要意义。

本文以某小区建设项目为研究对象，通过无人机对测区进行航测，获取该区域的点云数据，采用MATLAB软件编写克里金(Kriging)插值法程序，应用该程序对钻孔数据进行插值，在Civil 3D软件中建立地表曲面、土石分界曲面和设计开挖曲面，进而分别计算出工程中土方量和石方量，并对其精度进行了分析。

1 工程背景

该小区位于邯郸市峰峰矿区，场地南北约190 m，东西约180 m，场地内填土较多，平场后基坑开挖深度为10.5 m。场地地表大部分裸露，少部分区域存在荒草，地表覆盖物较为简单，便于开展航测。

2 无人机点云数据获取

土石方的量算精度由地形表达质量直接决定[4]。由于测区内存在不同程度的土堎和小土堆，RTK测量很难表示这些细小的地形变化，且效率低下。机载激光雷达具有精度高、点云密度大、效率高等优点[5]，故本次采用机载lidar对测区进行扫描，获取原始点云，并对原始点云去噪处理,剔除噪声点[6]。处理后点云如图1所示。

图1 点云数据

实地测量高程检查点15个，高程最大误差为8 cm，高程中误差为3.8 cm。

3 基于Kriging算法的钻孔数据插值

3.1 Kriging插值算法

Kriging插值法，又名局部估计，在地质统计学领域占有重要地位[7]。Kriging插值是将离散的钻孔数据转换为连续的地质曲面数据[8]。

Kriging插值法，在有限的区域中，使用一个线性组合对待插值点进行估计：

(1)

式中,Z(S0)为插值点；λi为第i个钻孔数据的权重；Z(Si)为第i个钻孔的值；N为钻孔数量。

权重λi利用式(2)求解：

(2)

式中,γ(xi,xj)为钻孔点的变异函数值；μ为拉格朗日常数。

估计方差利用公式(3)计算：

(3)

3.2 钻孔数据插值

在研究区周边共收集到15个可用钻孔数据，现将钻孔数据分为2类：一类为训练样本，共计11个钻孔；二类为检验钻孔，共4个。钻孔分布如图2所示。

作者采用MATLAB软件编写了Kriging插值算法的程序，应用该程序对研究区域进行格网插值，格网间距为5 m，插值结果如图3所示。

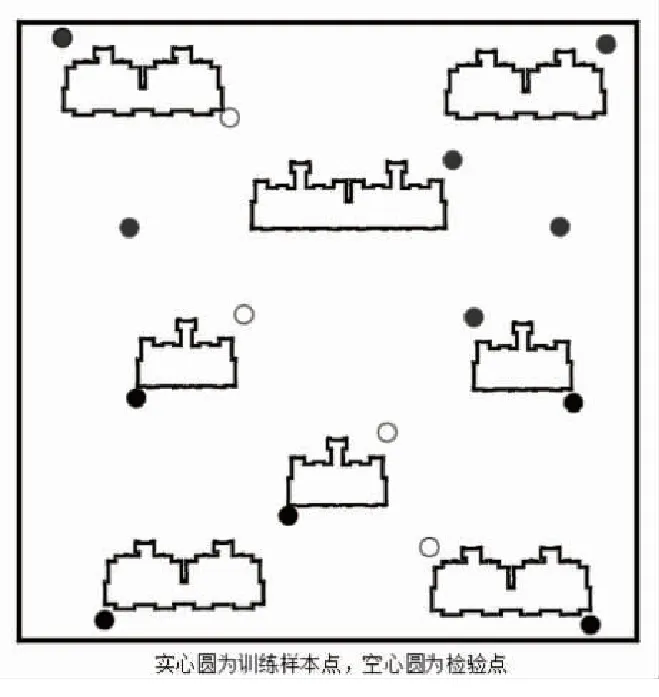
图2 钻孔分布图

图3 插值结果

3.3 插值精度评定

插值结果的精度从检验钻孔和插值标准差两方面进行评定。

采用Kriging插值法对4个检验钻孔进行单点插值，并与实测值对比，结果如表1所示。

表1 插值结果对比/m

表1表明：4个检验孔的插值结果中误差为0.27 m；ZK9插值误差最大，与ZK9距离训练样本较远有关。

根据式(3)，计算出每个插值点的标准差，如图4所示。

图4表明：由于插值区域中北部训练样本间距较大，故插值点的标准差偏大；由于插值区域东西两侧属于外延性插值，插值点的标准差有增大的趋势；插值点的标准差最大值为0.95 m，中误差为0.43 m。

以上两种插值精度的评定方法，计算出的中误差基本一致；根据检验孔计算的插值中误差更小，是由于检验孔均位于训练样本点内部，且数量较少。

图4 插值点标准差

4 土石方计算与精度分析

4.1 土石方计算

将点云数据、钻孔插值数据导入到Civil 3D软件中，分别建立地表曲面、土石分界曲面；根据设计文件，建立设计开挖曲面。应用Civil 3D的体积计算工具，根据地表曲面和设计开挖曲面计算出土石方挖方总量和填方量，根据土石分界曲面和设计开挖曲面计算出石方挖方量，进而得出土方挖方量、石方挖方量、填方总量。计算结果如表2所示。

表2 土石方计算结果/m3

4.2 土石方总量精度分析

本文中土石方总量是由点云数据和设计资料计算得到，将该方法与传统RTK测量结果进行对比并分析其精度。

采用RTK对测区进行测量，并用DTM法计算土石方总量。与根据点云数据计算的工程量进行比较，如表3所示。

表3 工程量结果对比

表3表明：两种方法计算结果差值比较小，采用点云数据计算土石方量是可行的；RTK法计算挖方量相较于点云数据少2 941 m3，主要是由于测区内存在类似坟包的土堆，RTK人工测量时进行了舍弃。

4.3 石方量精度估算

石方量的精度主要受土石分界插值点精度的影响。根据微积分理论，将开挖区域投影面划分为若干小方格，每个小方格尺寸为Δx×Δy，其对应的石方量为△x△y(H石-H设计)，则石方量可由式(4)表示：

V石=∑ΔxΔy(H石i-H设计i)

(4)

式中,H石i为第i个小方格对应的土石分界曲面的高程；H设计i为第i个小方格对应的设计曲面的高程。

将公式(4)变换后可得到公式(5)：

V石=ΔxΔy∑H石i-ΔxΔy∑H设计i

(5)

式中,ΔxΔy∑H设计i为常数项，根据误差传播定律可得：

(6)

式中,mv石为石方量的中误差；mh石i为第i个土石分界曲面插值点标准差。

取Δx=Δy=1，即格网间距为1 m，利用式(3)计算每个插值点的标准差，并代入式(6)中，可得石方量中误差为：

则石方量的相对中误差为：

K=mv石/V石=1.1%

5 结 论

(1)通过与RTK测量结果进行对比，采用无人机点云数据计算土石方量是可行的，且效率更高、地形表达更详细；

(2)经理论计算，采用克里金插值后的钻孔数据计算石方挖方量的相对误差为1.1%，精度是可靠的；

(3)应用点云数据和钻孔数据，采用Civil 3D软件实现了土方量和石方量的分别计算，且精度可靠效率更高。