一类零膨胀广义线性模型极大似然估计的相合性与渐近正态性*

于 洋，侯 文

(辽宁师范大学 数学学院，辽宁 大连 116029)

1 引 言

广义线性模型的概念由 Nelder和Wedderburn(1972)[1]首先提出.他将经典线性回归模型进行了延拓，并针对新模型确定统一的理论，且在其论文中详细地讨论了广义线性模型的假设、构成及其参数估计.MaCullagh和Nelder(1989)[2]第一次将广义线性模型引入到保险精算学中,认为指数型分布族可以通过适当的线性变换完成线性化，该线性化的模型包括泊松、二项、负二项等分布.但是存有广义线性模型不适用的情形，比如在分析离散数据时常常出现零观测值过多的情形.如果强行采用广义线性模型拟合将导致拟合效果不佳且容易对分析结果产生失真的解释.零膨胀广义线性模型可用在这些情形中，如零膨胀泊松回归模型，该模型用于分析生产过程中产品所含有的瑕疵数量，进一步，将零膨胀泊松回归模型扩展到零膨胀负二项回归模型，并将该模型应用到顾客信用卡不良记录的探究中.Deng和Paul(2000)[3]对零膨胀广义线性模型的参数给出了得分检验统计量.但是现有的 大多数文献打都是关注于模型的应用，较少涉及零膨胀广义线性模型极大似然估计的相合性和渐近正态性等大样本性质.借鉴Fahrmeir和Kaufmann(1985)[4]对广义线性模型极大似然估计的大样本性质的研究结果，在一定的正则条件下，证明零膨胀广义线性模型极大似然估计的相合性和渐近正态性等性质应该是有价值的.

2 一类零膨胀广义线性模型

f(y,θ)=c(y)exp {θy-b(θ)}dγ.

(1)

其中，θ为自然参数，b(θ)和c(y)是已知函数.这两个函数必须满足以下条件：

b(θ)的二阶导数存在并且大于零；

c(y)是独立于参数θ的函数.

由于零膨胀现象经常发生在计数数据中，例如，泊松分布，二项分布，负二项分布等，故在此背景下，零膨胀指数族定义为

其中，f(y,θ)为式(1)所示的单参数指数分布族密度函数，记作Y～f(y,θ,ω)，θ,ω为参数.其均值和方差为

E(Y)=(1-ω)μ=(1-ω)b′(θ),

Var(Y)=(1-ω)(b″(θ)+ω{b′(θ)})2.

零膨胀广义线性模型结构如下：

(1)模型的响应变量为Yi，Yi～f(y,θ,ω)，且Yi相互独立，i=1,2,…,n；

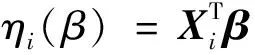
(3)联结函数g是一个单调可微的函数，它体现了随机成分的期望值与系统成分之间的联系，即E(Yi)=μi=g-1(ηi).

对数似然函数为

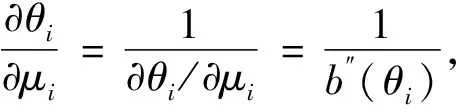
其score向量为

sn(δ)=(s0(δ),s1(δ),…,sp(δ),sp+1(δ))T,

(2)

其中，

又

进一步求导，可得观测值矩阵为

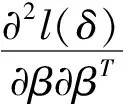
(3)

Fisher信息阵Fn(δ)=EδHn(δ),

由E(I(yi=0))=P(Yi=0)=ω+(1-ω)f(0,θi)和

E(I(yi>0))=P(Yi=y)=(1-ω)f(yi,θi),

(4)

为了方便，先设定一些特殊的记号.令λminA和λmaxA分别表示矩阵A的最小特征根和最大特征根，用AT表示矩阵A的转置矩阵，A1/2表示正定矩阵A的Cholesky分解中左平方根的下三角矩阵，且其对角元素为正，即A1/2(A1/2)T=A.

为了表示方便设定AT/2=(A1/2)T，A-T/2=(AT/2)-1，A-1/2=(A-1/2)-1.

用‖·‖表示一个矩阵的谱范数，一个实值矩阵A的谱范数为

‖A‖=(λmax(ATA))1/2，

Hn(δ)和Fn(δ)分别表示零膨胀广义模型参数δ的观测信息阵和Fisher信息阵.

此外分别将sn(δ0)、Fn(δ0)、Eδ0记为sn、Fn、E.

定理1需要在以下假设下进行证明：

(2){Xn,n≥1}⊂Kx，Kx⊂RP+1是一个紧集，

(3)假设B⊂Rp+1是一个开集且δ0是集合Kδ:=B×Ω的内点，其中Ω=[0,1].

3 相关引理及证明

为了证明定理1，需要证明以下引理.

若函数u(·)在[0,)是非负的，有

证明第一个式子通过下面等式证明

由E(I(y>0))=P(Y=y)=(1-ω)f(y,θ).

又由函数u(·)在[0,)是非负的，显然有

证明根据Ramesh(1974)[5]中定理2.2，有递推公式

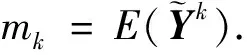
引理3设Qk(y)为k阶多项式，其系数是关于x，δ,δ0的连续函数且系数为正，令Yi～f(yi,θi,ω),i=1,2,…,n.如果条件(1)-(3)成立，则

证明在条件(1)下，对∀n∈N，邻域Nn(ε)是紧集，且对于∀ε>0，当n→时，Nn(ε)收敛于δ0.因此由引理3.1和3.2以及多项式Qk(y)系数的连续性，有

引理4在条件(1)-(3)下，当n→时，，其中N(0，Ip+2)是p+2维正态分布，且其均值为0，协方差矩阵为Ip+2(Ip+2为p+2阶的单位阵).

由Cr不等式的一个展开式

(5)

有E‖sni‖3≤C(E|s0,i|3+…+E|sp,i|3+E|sp+1,i|3).

由式(5)得

将其最后一步拆成两部分来证明.

再由Cauchy-Schearz不等式和引理3.2，得

由此证得引理4成立.

需证明

(6)

(7)

(8)

(9)

(10)

由于式(8)、式(9)和式(10)有相似的结构，只证明式(8)成立，其他可类似处理.

为得到式(8)，只需证

(11)

(12)

其中:

而式(9)和式(10)由大数定律可知成立.

由式(7)，有

(13)

(14)

(15)

由于式(13)、式(14)和式(15)有相似的结构，只证明式(13)成立，其余可以类似处理.

当n充分大时，由δ∈Nn(ε)，由式(4)中frs(δ)的连续性，可得式(13)成立.

由此证得引理5成立.

4 主要结果及证明

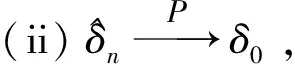
证明令∂Nn(ε)表示Nn(ε)的边界，由条件(1)知，当n→时，Nn(ε)收敛于δ0.

则 ln(δ)-ln(δ0)<0，∀δ∈∂Nn(ε).

(16)

下面证明对∀η>0，∃ε>0和n1使得对所有n≥n1，有

P(ln(δ)-ln(δ0))<0，且对∀δ∈∂Nn(ε)≥1-η成立.

(17)

由此可知式(17)成立.

因此可以推得定理1的(i)成立.

由引理4和引理5即可推得定理1 的(ii)成立.

5 结 论

通过讨论响应变量为单参数指数族且在零点处膨胀的广义线性模型的大样本性质，表明零膨胀广义线性模型具有与广义线性模型相类似的渐近性质.另外，定理的渐近结果也适用于一些离散型模型，如零膨胀负二项回归模型，零膨胀泊松回归模型，等等.