基于GARCH族优选模型的舰船器材消耗预测

吴雯雯，陈振林

（海军航空大学，山东烟台264001）

GARCH（Generalized Autoregressive Conditional Heteroscedasticity）族模型，即广义自回归条件异方差模型，主要研究时间序列变量的方差变化规律[1]。

舰船器材消耗量受设备生命周期、任务类型、海洋环境以及使用设备人员的技能水平等因素影响，消耗量数据序列的方差不一定随着时间的推移而始终增加。

舰船器材消耗量有时会出现增加，有时可能又会减少，有时会出现增减交替的情况，甚至可能还会伴随着丛集效应的出现，高峰厚尾特征比较突出。

为了有效解决上述问题，可以选择优选GARCH族条件异方差模型来拟合数据序列的变化过程，以提高回归参数估计的准确性。

1 消耗数据分析

选取2015年至2019年某舰船器材月消耗数据序列作为研究对象。

1.1 数据基本特征

将某舰船器材消耗量的数据序列以散点图的形式表示，如图1所示。

由图1可知，随着时间的推移，数据序列呈现出不规则的分布，并且随着舰船使用年限的增加，消耗量的数据总的来说呈现出不规则增加的趋势。

图2 为消耗量数据序列特征图。由图2 可知，该数据序列的直观表征是一个非平稳序列。

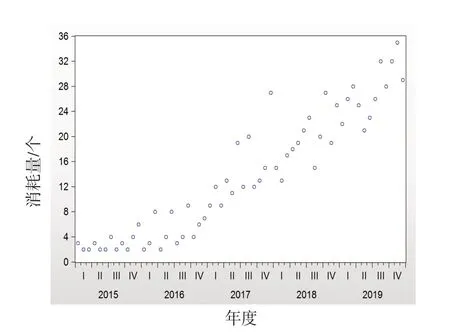
图1 舰船器材消耗量数据散点图Fig.1 Scatter plot of warship equipment consumption data

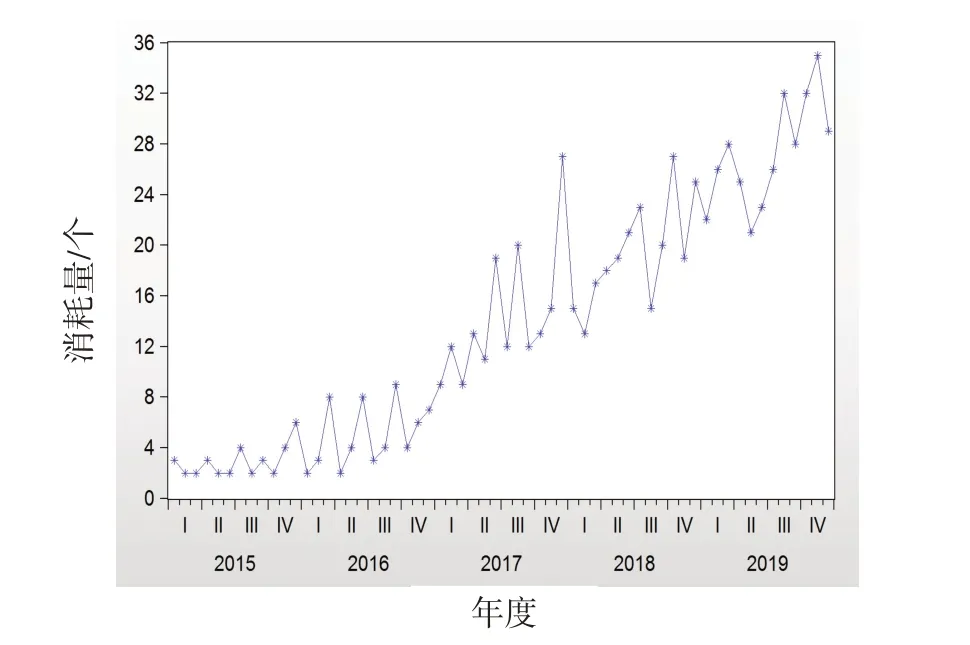
图2 消耗量数据序列特征图Fig.2 Consumption data sequence feature chart

1.2 单位根检验

为了检验消耗量数据时间序列的平稳性，有必要进行单位根检验，采用实证分析中最常用的ADF（Augmented Dickey-Fuller Test）检验。如果存在单位根，则说明时间序列是非平稳的[2-3]。ADF检验由下面公式完成：

式（1）～（3）中：xt为因变量；δ 为参数；t 为时间变量；m 是因变量的滞后阶数；βt 为时间趋势项；α 为截距项；εt是独立同分布，且服从均值为0、方差为σ2的正态分布。

原假设均为H0∶δ=0。依次按照式（3）、（2）、（1）的顺序进行检验。若检验拒绝H0∶δ=0，即原序列不存在单位根，为平稳序列，停止检验。否则，继续检验，直至完成式（1）。

对某类器材消耗数据时间序列的单位根检验可以按照3个步骤进行：①对消耗量原始数据序列进行单位根水平检验，以确认消耗量原始数据序列的平稳性；②如果检验结果为原始数据序列是不平稳的，则对消耗量原始数据序列进行一阶差分检验，检验一阶差分后的数据序列的平稳性；③如果一阶差分后的数据序列仍然不平稳，则对消耗量一阶差分数列再进行二阶差分处理，并检验其平稳性。

1）消耗量数据序列的单位根水平检验。对消耗量的原始序列进行单位根水平检验，检验结果显示，ADF 检验的t=0.609 748>-2.914 517，即：明显大于5%的显著性水平。因此，这说明消耗量的原始数据序列具有明显的非平稳性，须进行一阶差分数据序列的单位根检验。

2）一阶差分数据序列的单位根检验。对一阶差分数据序列进行单位根检验，检验结果显示，ADF 检验的t=-8.150 79<-2.914 517，即：明显小于5%的显著性水平。因此，这说明一阶差分数据序列是平稳的。但是，D(Y(-2),2)对应的P 值稍大。因此，有必要进行二阶差分序列的单位根检验。

3）二阶差分数据序列的单位根检验。对二阶差分数据序列进行单位根检验，检验结果显示，ADF 检验的t=-7.882 63<-3.498 692，即：明显小于5%的显著水平值。因此，二阶差分数据序列是平稳的。

1.3 二阶差分数据序列的特征分析

对数据序列的一阶和二阶差分处理后，可以得出其差分序列基本属于稳定的时间序列，但是其残差序列的波动性呈现出异方差特征，如图3所示。

图3 二阶差分后的数据序列图Fig.3 Data sequence diagram after second-order difference

1.4 残差序列的峰度与偏度分析

按定义，峰度是所选取样本序列的标准四阶中心矩。偏度则是所选取样本序列的标准三阶中心矩[4-5]。

峰度公式为：

式（4）中：K 为峰度；n 为正整数；xi为随机序列变量；μ 是均值；σ 是标准差。

当峰度为0 时，说明数据序列的总体分布与正态分布陡缓程度是一致的；当峰度大于0时，说明数据序列的总体分布与正态分布相比呈尖顶峰状态；当峰度小于0 时，说明数据序列的总体分布与正态分布相比呈平顶状态。

偏度公式为：

式（5）中：S 为偏度；xi为随机序列变量；μ 为均值；σ为标准差。

当偏度为0 时，说明数据序列分布形态与正态分布形态一致；当偏度大于0时，说明数据序列分布形态与正态分布相比为右偏状态；当偏度小于0时，说明数据序列的分布形态与正态分布相比为左偏状态。

对于舰船器材消耗量数据的残差序列进行峰度和偏度分析，可以得出峰度与偏度的结论，见图4。

残差数据序列的尖峰厚尾特征明显，峰度K=3.528 926>0 ，说明比正态分布的顶峰更高。因此，具有尖峰特征。偏度S=0.248 795>0，说明比正态分布右偏。这与ARCH（Autoregressive Conditional Heteroscedasticity）模型条件基本吻合，可以尝试分析其异方差的显著性，来选择是否采用GARCH 族模型进行预测建模分析。

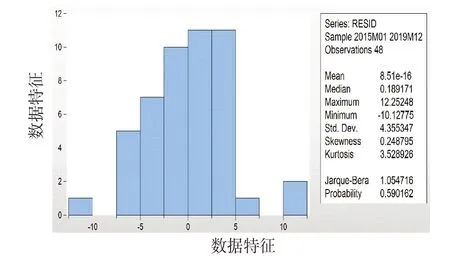
图4 峰度与偏度分析图Fig.4 Analysis of kurtosis and skewness

2 模型构建

2.1 数据序列相关性及残差序列ARCH效应检验

对二阶差分数据序列进行标准相关性检验，伴随概率P 值均大于0.05，一阶相关性检验部分P 值大于0.05。因此，须对二阶差分序列进行二阶相关性检验，检验结果如表1所示。由表1可见，P 值均小于0.05，这说明仅二阶差分序列具有自相关性。

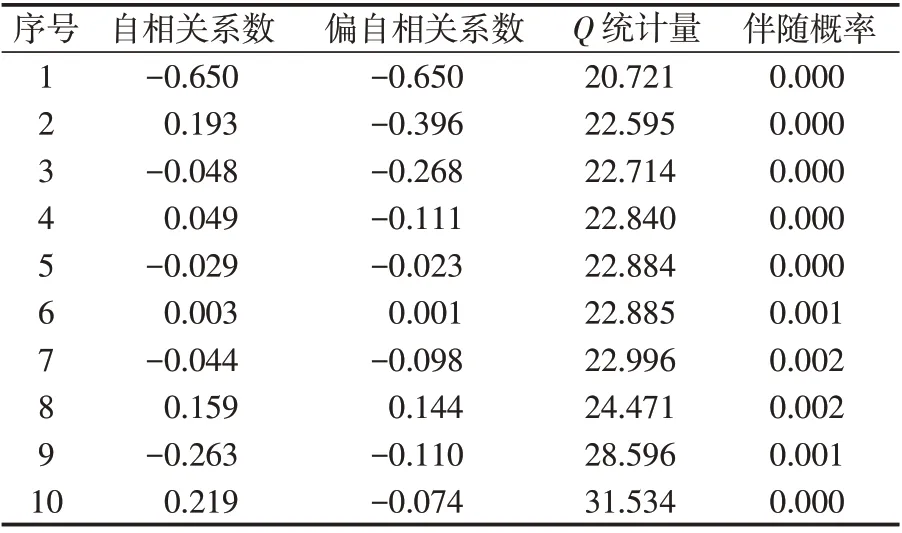
表1 二阶差分数据序列的二阶相关性检验Tab.1 Second-order correlation test of the second-order differential data sequence

对残差序列进行数据特征分析，如图5 所示。由图5可知，实际的残差波动特征明显，中间部分有明显的丛集效应特征。为了使构建的模型能够准确地反映舰船器材消耗的现实状况，有必要在ARCH 和GARCH 模型建立的过程中，检验数据序列的条件异方差性[6]。

对残差数据序列进行ARCH 效应，即进行LM（Lagrange Multiplier）检验，检验结果如表2 所示。由表2 可知，当滞后项选择8 时，所构造的统计量，其P值小于0.05。因此，说明残差数据序列存在ARCH 效应。

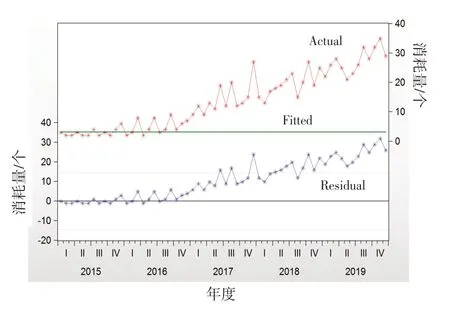
图5 残差序列的特征分析Fig.5 Feature analysis of residual sequence

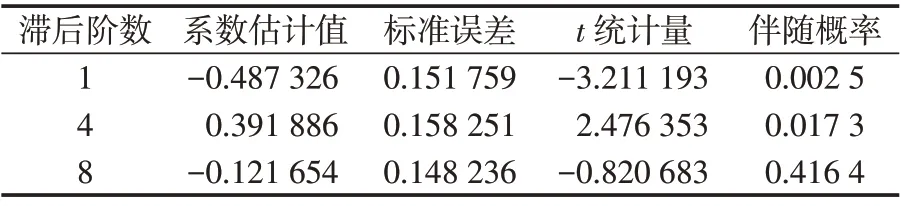
表2 残差数据序列的ARCH效应检验Tab.2 ARCH effect test of residual data sequence

2.2 ARCH模型的建立

按照恩格尔的假设，随机变量是具有一阶AR(p)自回归过程：式（6）中：xt为随机变量；β 为参数；t 为正整数；p 为滞后阶数；εt为随机扰动项。

能够同时满足{εt} 是一个独立同分布白噪声过程，并且满足E(εt)=0，D(εt)=σ2。如果随机变量xt为一个平稳过程，则其特征多项式的根均应置于单位圆外，即可以通过单位根检验，确定随机变量序列的平稳性状况。

如果存在一个随机过程{εt} ，且

式（7）中：εt为随机扰动项；α 为参数；q 为滞后阶数；εt-1为εt的滞后1阶项；εt为q 阶随机扰动项的函数，可记作εt～ARCH(q)。

为了确定ARCH效应的滞后阶数，分别将滞后阶数按照升序进行检验。当滞后阶数为9 时，ARCH 效应不显著。这样即可确定ARCH 效应的滞后阶数为8，建立ARCH模型，并对模型参数进行估计[7-8]。

模型的滞后项有8项，显然，滞后项过多会使模型计算十分繁琐，且AIC=6.904 8，值比较大。因此，考虑采用GARCH模型。

2.3 GARCH模型的构建

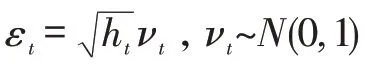
当阶数q →∞时，为了计算滞后阶数，设条件异方差ht表达式如下：

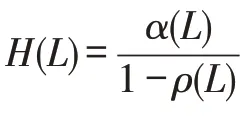
变换后：

式（9）中：k0=(1-ρ1-ρ2-…-ρp)α0为常数项；ht为条件异方差；ρ 为参数。

此时，εt～GARCH(p,q)。

由此可见，ht分别是时间序列的滞后随机误差平方和滞后条件方差的线性函数。GARCH 模型从ARCH 模型的残差特性分析入手，将高阶的ARCH 模型进行简化处理，使模型识别和参数估计比ARCH模型更容易，也更具一般性。

当p=q=1 时GARCH 模型的简化模型即为GARCH(1 ,1) ，即

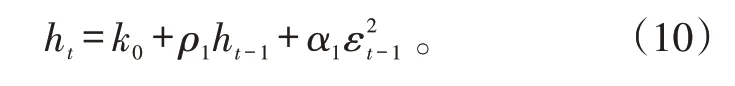
式（10）中：k0>0；ρ1≥0；α1≥0。

则εt～GARCH(1,1)是平稳过程的充分必要条件：α1+ρ1<1。

运用GARCH 基本模型对参数进行极大似然估计。

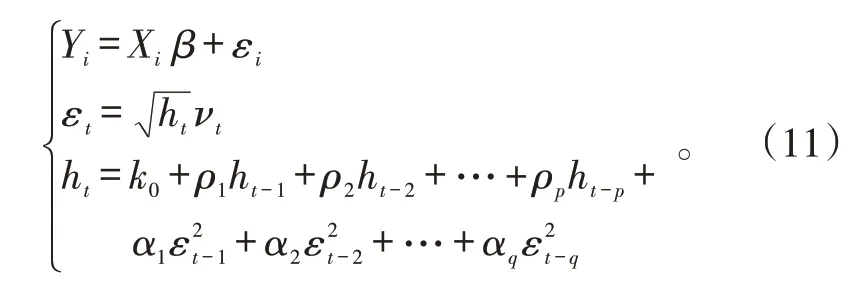
式（11）中：Xi为解释变量；Yi为其相应的响应变量；β 为未知回归参数。

设观测集为：

式（12）中：Xi为解释变量；Yi为其相应的响应变量；q为滞后阶数。

则GARCH模型的参数集可以表示为：

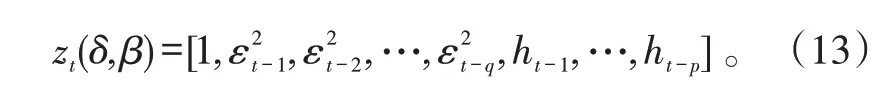
式（13）中：δ=[k0,α1,…,αq,ρ1,…,ρp] ；β 和δ 为未知参数。

则GARCH模型的极大似然函数为：

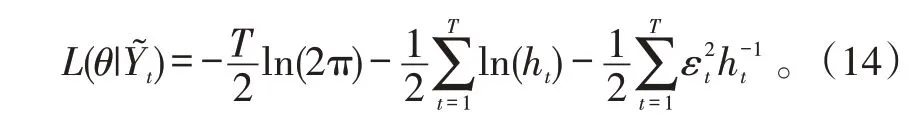
式（14）中：T 为正整数；ht为条件异方差。

取极值可得：

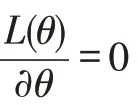
分别构建GARCH(1 ,0 )和GARCH(1 ,1) 模型进行比较，并进行ARCH 效应分析，以获得更能准确反映消耗量现实状况的模型[9-10]。

由GARCH一般模型可知：

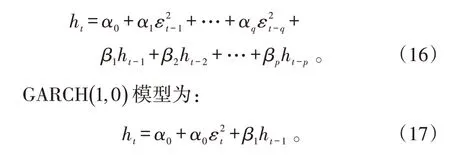
GARCH(1 ,1) 模型为：

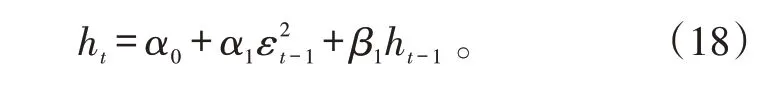
式（16）～（18）中：ht为条件异方差；α、β 为参数；t 为正整数；p、q 为滞后阶数。

对GARCH(1 ,0 )模型和GARCH(1 ,1) 模型进行参数估计与ARCH 效应检验，结果显示GARCH(1 ,1) 模型的AIC 值较小。因此，可以选择GARCH(1 ,1) 模型作为消耗量预测备选模型[10-13]。

GARCH(1 ,1) 模型为：

参数估计后，可以得到：

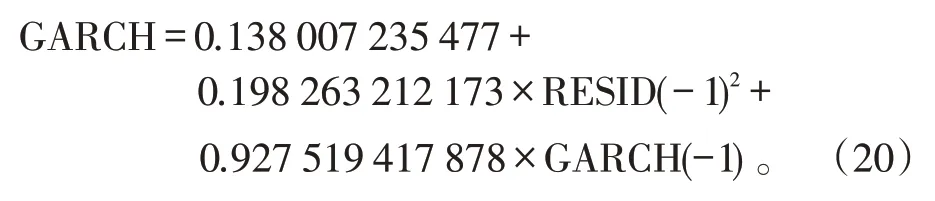
3 GARCH族模型比较优选

对数据序列进行GARCH 族模型参数估计与检验，根据AIC 准则与所构建的GARCH(1 ,1) 模型进行比较和优选，以选择精度更高的模型对舰船器材消耗量进行准确预测。AIC 准则，由日本统计学家赤池弘次在1974 年提出，建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。从一组可供选择的模型中选优，通常选择AIC值最小的模型。

3.1 TGARCH杠杆效应检验

TGARCH（Threshold Garch）模 型，简 单 修 正GARCH模型来描述正负项干扰对波动率的非对称影响后果，可以有效描述非对称波动，条件方差使用指数形式表示，放松了对模型参数的限制。TGARCH模型的条件方差可表示为：

ut-1>0 时，有Dt-1=0，表示正向干扰；ut-1<0 时，有Dt-1=1，表示负向干扰；ut-1=0 表示干扰因素对条件方差的影响是均衡的[14-15]。

对TGARCH模型杠杆效应进行分析，参数估计如表3所示。

表3 TGARCH杠杆效应检验Tab.3 TGARCH leverage effect test

由表3 可知，ARCH 项和非对称项对应的P 值均大于0.05。因此，存在杠杆效应。同时可知，运用TGARCH模型的AIC=6.807 12。

3.2 EGARCH效应检验

Nelson[16]在GARCH 模型假设的基础上，引入EGARCH 模型，重新构造了非对称的模型，对参数的非负约束条件进行了放松，并将条件方差表示为对数形式，即：

式（22）中：εt-1为随机干扰项；为随机干扰项的方差；ω、β、α、γ 均为决定性参数。

因为采取了对数形式的变换，所以条件方差不会出现负值。对EGARCH 模型进行参数估计和显著性检验，结果如表4 所示。由表4 可知，该模型的AIC=6.825 296。

表4 EGARCH效应检验Tab.4 EGARCH effect test

3.3 PGARCH检验

建立PGARCH模型并检验其GARCH效应。

PGARCH 模型主要用于解决具有周期性特征的时间序列预测问题。当不具备周期性特征时，则PGARCH 模型就是GARCH 模型。也就是说，GARCH 模型其实是PGARCH 模型的一种无周期性特征的特殊形式。这里将GARCH( )1,1 拓展为PGARCH，用以比较2 个模型对舰船器材消耗量预测精度的优劣。

设{ Xt} 为时间序列数据集，如果存在周期为S 的PGARCH(p,q)，则：

式（23）、（24）中：σ2为随机干扰项的方差；误差序列{εt} 服从独立同分布；ωt、αt,i、βt,j均为周期S 的函数。

首先，进行系数梯度变化情况分析，如图6 所示。由图6可知，系数的梯度，在2017年下半年开始C（1）、C（2）趋于平稳，C（3）、C（4）变化幅度减小，但是还是有一定的变化的[17]。更多阶数的系数及数据序列的参数估计情况，如表5所示。由表5可知，时间序列没有明显的周期性。因此，不适合建立PGARCH模型来对舰船器材消耗情况进行预测，且运用该模型的AIC=6.986 452，值也是比较大的。

图6 系数的梯度变化情况图Fig.6 Diagram of the gradient variation of coefficients

表5 PGARCH模型参数估计表Tab.5 Parameter estimation of PGARCH model

3.4 模型比较优选

按照模型优劣比较的AIC 准则，可以通过比较GARCH 族各个模型的AIC 值大小来确定终选模型。在上述讨论的模型中，GARCH(1 ,1) 的AIC值最小，滞后阶数最少，便于求解，预测精度高。因此，可以确定GARCH(1 ,1) 为消耗量预测的最优模型[18-20]。

4 实例分析

以舰船器材2015年至2019年的消耗量数据序列为研究对象，运用GARCH(1 ,1) 模型，对2020 年上半年可能的消耗量进行预测。舰船器材消耗量GARCH值的变化趋势，见图7。由图7 可知，GARCH 值随着时间总的变化趋势是趋于平稳的。因此，可以运用上述所构建的GARCH(1 ,1) 模型进行消耗趋势预测。2020年上半年的消耗量变化趋势情况，如图8所示。

简化后模型为：

具体的预测结果，如表6所示。

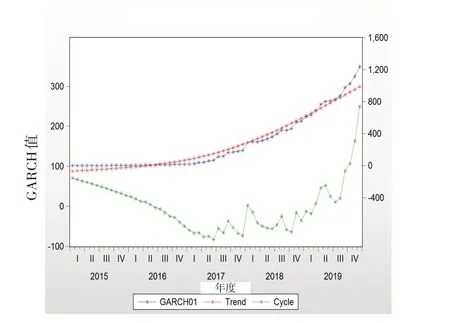
图7 GARCH值的变化趋势Fig.7 Trends of GARCH values

图8 2020年上半年器材消耗量变化趋势图Fig.8 Trends of equipment consumption in the first half of 2020

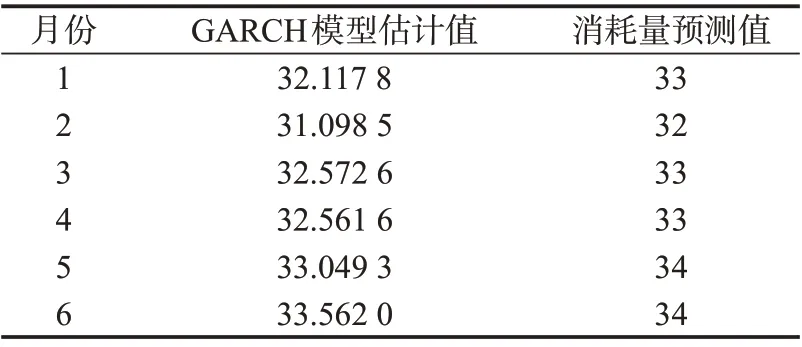
表6 2020年上半年器材消耗量预测值Tab.6 Forecasts of equipment consumption in the first half of 2020

5 结语

从上述模型建立与拟合的过程可以看出，舰船某类器材消耗规律与其他类器材相比较，具有明显的随机性特征。尽管波动性比较强烈，但是有一定的规律可循，尤其是其ARCH 效应十分显著。但是，滞后阶数过多，影响了模型的计算效率。采用GARCH 模型进行拟合，可以较好地满足滞后阶数少，预测精度高的要求。

GARCH( )1,1 模型可以实现对舰船器材消耗的准确预测。当然，这里的模型还只是针对舰船器材消耗实际序列进行的拟合，考虑到器材消耗的影响因素较多，只是根据数据序列的处理来预测消耗量还是有一定局限性的，有必要考虑多种因素的影响，来进一步完善拟合模型，以期更加精确地预测某类器材消耗的现实情况。