四路鉴相器瞬时测频解模糊方法研究

李国君，朱泽龙，岳付昌

（1.92941部队；2.91475部队，辽宁葫芦岛125001）

微波信号频率测量在电子对抗和空馈式雷达目标模拟领域占据重要地位。比相法瞬时测频实时测量到达脉冲信号载频，为信号上下变频提供参考信号，是后续信号检测和处理的基础，对脉冲信号而言，具有高频率截获概率、高测频精度等突出优点[1-4]。

比相法数字瞬时频率测量典型电路包括放大器、功分器、鉴相器和量化编码电路等[5]。因为角度信息的重复等原因，实际工程中测得的角度变化范围控制在360°内。为解决角度信息的模糊和多值，一般采用多个测频单元组合使用[6]。本文主要研究四路鉴相器解模糊问题，采用由低位向高位解模糊，并给出了具体实现方法。

1 比相法瞬时测频原理

比相法瞬时测频是目前应用较广泛的一种瞬时测频技术，其核心是把信号的频率信息转换成相位信息（角度信息）；然后，根据相位所对应幅度信息推算出信号频率[7-9]。

基本测频单元主要由2 部分构成，包括1 个功分器和2 条长度不等的延迟传输线，基本组成如图1 所示。

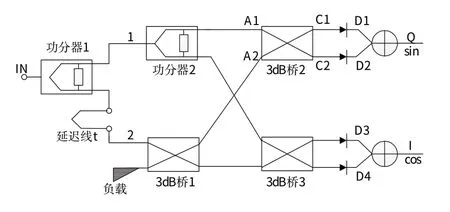
图1 基本测频单元组成图Fig.1 Diagram of basic frequency measurement unit

功分器将1 路信号分解为2 路，然后分别经过不同长度的传输线（1路不延时，另1路延迟特定时间），2路信号对应一确定相位差Δϕ，可表示为：

式（1）中：l 为延迟线长度；c 为光速；f 为信号频率。

相位差Δϕ 是一个正比于频率的量，其延迟线长度越大，2 路信号的相位差越大。在完成频率到相位的转换后，接下来的问题是如何将得到的相位差值转换成可以测量的幅度信息。完成频率到幅度转换的器件为鉴相器[10-14]，鉴相器是一个简单的和差合路器，因为2 个高频信号在叠加时，合成信号的幅度与信号的相位差有关，因而可以用它来表示2 路信号的相位差。为了消除信号本身幅度对测量结果的影响，就须要同时获得这2 个信号的和与差，最常用的器件是3 dB 定向耦合器，它能够将输入信号分为2 个等幅且具有90°相位差的信号。

图1中，假设输入的微波信号为：

延迟线延迟时间为τ，通过功分器后，在A1和A2处得到的2路信号为：

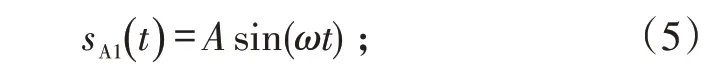
2 路信号通过3 dB 定向耦合器之后，在C1 和C2处得到的2路信号为：

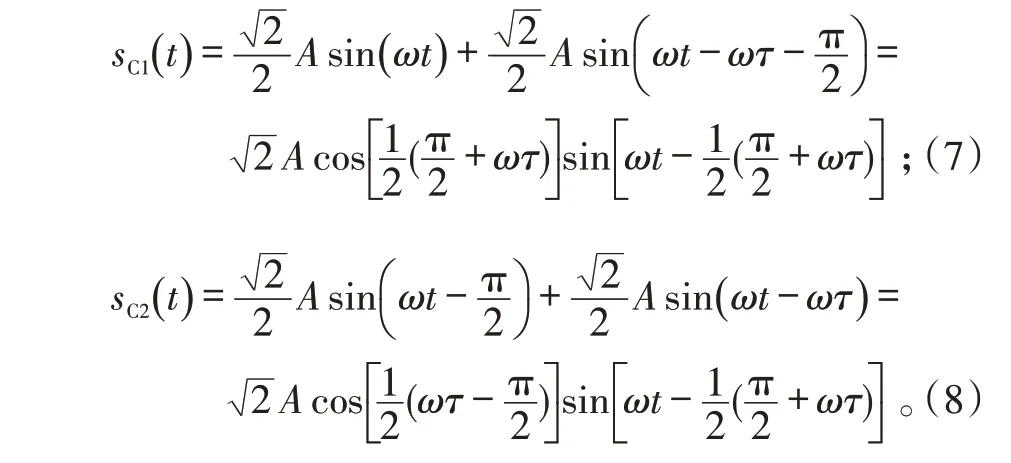
经过平方率检波和低通滤波之后，D1 处和D2 处的信号形式为：

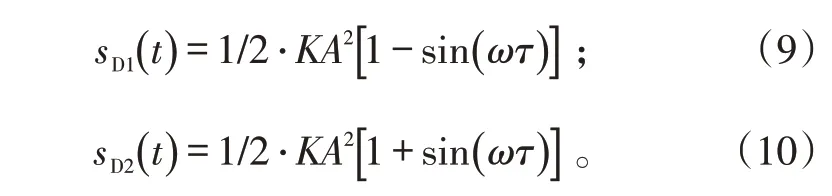
同理，可以得到在D3处和D4处的检波信号形式为：

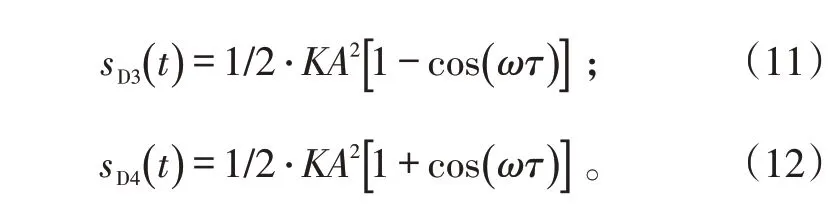
式（10）和式（9）相减得：

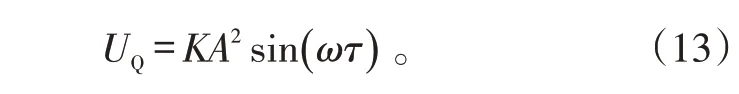
式（11）和式（12）相减得：

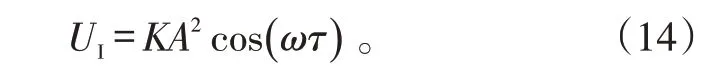
在生成呈正弦、余弦变化的信号后，工程实现中一般不直接按式（13）、（14）计算反三角函数，而是将加权后正余弦信号经量化电阻网络数字化，得到代表相位值的多位二进制数，具体方法可见文献[15-17]。

2 四路鉴相器瞬时测频具体实现

在鉴相器中，延迟线长度的选择是一个重要问题，通常选择延迟比的范围在2 ∶1 到8 ∶1 之间，小的延迟比要求更多的微波鉴相器，对每个鉴相器输出信号数字量化时，可用较低的分辨率，降低了对数字编码电路的要求。大的延迟比可减少鉴相器数目，但对每个鉴相器输出信号数字量化时要用较高的分辨率，会增加数字编码电路的复杂度。

为保证高测频精度和低系统复杂度，工程上一般采用延迟比为4 ∶1。鉴相器数量为4个，前3个鉴相器分别提供四位编码输出，第4 个鉴相器提供六位编码输出，解模糊后相位码数为12 位，利用四路鉴相器实现瞬时测频原理图如图2所示。

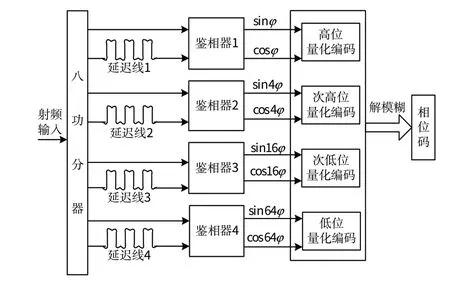
图2 四路鉴相器测频电路组成图Fig.2 Circuit composition of 4 routes phase discriminator frequency measurement

3 多鉴相器测频解模糊方法

采用多鉴相器法进行测频时，会出现测频模糊问题，以第1 路和第2 路测频为例，第1 路测频相位变化为0～2π ，当延迟比为4 ∶1 时，第2 路相位变化为0～8π，第3、4 路鉴相器相位变化以此类推[18-20]。采用四路鉴相器实现瞬时测频时，短延迟支路输出代码是整个相位代码的高位，长延迟支路的输出代码是整个相位代码低位，解模糊方法采用由低位向高位解模糊方法，具体解模糊过程如下：

四路鉴相器输出相位码由高位向低位分别为ϕ1、ϕ2、ϕ3、ϕ4，将每个鉴相器编码补齐为12位。具体方法如表1所示。

表1 四路鉴相器解模糊编码方法Tab.1 Coding method of solving ambiguity for 4 routes phase discriminator

在ϕ2～ϕ4编码中，××表示数值存在模糊和不确定性，具体值可能为0或1，解模糊步骤如下：

1）利用ϕ4码解ϕ3码的模糊，得到中间对位的ϕ5码；

2）利用ϕ5码解ϕ2码的模糊，得到中间对位的ϕ6码；

3）利用ϕ6码解ϕ1码的模糊，得到最终相位码ϕ7，根据ϕ7码可得利用四路鉴相器测频的输入射频信号频率。

4 解模糊算法典型实现

4.1 解模糊算法举例

1）ϕ4码解ϕ3码的模糊。取ϕ3的前8 位，即ϕ′3=10100000，ϕ4的前8 位为ϕ′4=××101100，其中×× 代 表4 种 可 能 数 值 分 别 为00、01、10、11，令ϕ( k )= |ϕ′3-ϕ′4|，其中绝对值最小时所对应的××值即为中间对位后的ϕ5码值，经计算10 码对应相位差最小，ϕ5码值为ϕ5=10101100。

2）ϕ5码解ϕ2码的模糊。取ϕ2的前10 位，即ϕ′2=0110000000 ，ϕ5的前10 位ϕ′5=××10101100 。其中，××代表4 种可能数值分别为00、01、10、11，令ϕ( k )= |ϕ′2-ϕ′5|，其中绝对值最小时所对应的××值即为中间对位后的ϕ6码值，经计算01 码对应相位差最小，ϕ6码值为ϕ6=0110101100。

3）ϕ6码解ϕ1码的模糊。取ϕ1的前12 位，ϕ6的前12 位为ϕ′6=××0110101100，与ϕ1码进行解模糊，计算过程与1、2 相同，经计算10 码对应相位差最小，最终的相位码ϕ 码值为ϕ=100110101100。

4.2 解模糊结果分析

如果取ϕ1～ϕ4编码输出的编码值按照由高位至低位拼接的相位码即a11a10b9b8c7c6d5d4d3d2d1d0，该值与解模糊结果是相同的，这只是适用于4.1 中举例所用编码的结果，不具有普遍性。

为了说明该问题，以ϕ4码解ϕ3码的模糊过程为例，假设ϕ4码解模糊时前8位为ϕ′4=d7d6d5d4d3d2d1d0（×× 用d7d6表示），ϕ3的前8 位为ϕ3=c7c6c5c40000，|ϕ3-ϕ4|可表示为

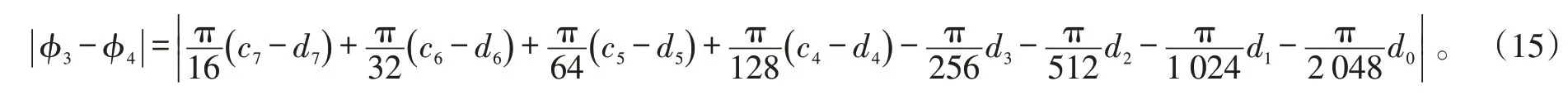
根据式（15），如果d0～d5均为1、c4～c5均为0，当c7=d7、c6=d6时，此时相位差绝对值为63π/2 048，当c7=d7、c6=1、d6=0 时，此时相位差绝对值为π/2 048，解模糊结果应为ϕ′4=c7d6d5d4d3d2d1d0，而不是直接对位的c7c6d5d4d3d2d1d0。

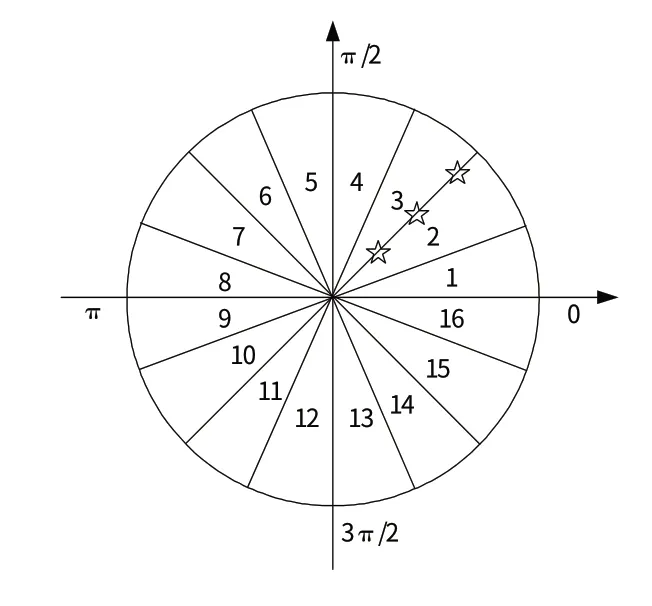
图3 4位相位码弧度划分原理图Fig.3 Radian division of 4 bite phase code

对于某一具体相位值，该值可能落在图3 中第2相位区间和第3 相位区间的交线上，如图3 中星号所示，此时相位编码出现就会出现模糊，增加相位编码位数时，即是将整个2π 弧度继续划分成更小的相位区间，并实现模糊相位的重排，通过缩小相位值区间范围的方法，能够解决相位模糊问题。

5 结束语

比相法瞬时测频是解决实时频率测量的重要方法，本文从瞬时测频原理出发，设计了比相法瞬时测频的具体实现方式，并对四路鉴相器测频解模糊问题进行了深入研究，给出了典型算法举例，分析了解模糊结果，具有一定的理论深度，可为工程技术人员提供有益参考。