杨氏双缝干涉光程差近似计算的弱化条件分析

张 勇，牟朝霞，刘存海，柳 叶

（1.山西农业大学信息学院，山西晋中030800；2.海军航空大学，山东烟台264001）

杨氏双缝干涉实验是光具有波动性的重要例证，也是大学物理课程中波动光学部分的重要内容[1-2]。几乎所有的工科院校大学物理教材中，都利用该实验阐述光的分波阵面干涉理论。文献[3-6]几乎采用同样的近似方法得出两束相干光的光程差。如图1 所示，各物理量含义如下[7-8]：a、b 代表两束光的光程；D代表观察屏与双缝间垂直距离；d 代表双缝间距；x代表观察屏P 点坐标，则δ=b-a 为：

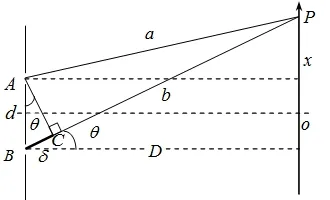
图1 杨氏双缝干涉实验Fig.1 Young’s double-slit interference experiment

该类方法中一般采用了以下3个近似条件[9-13]：

1）当D>>d 时，δ ≈——BC=d sin θ；

2）θ 很小，tan θ ≈sin θ；

条件1 满足远场干涉条件，条件2 满足近轴干涉条件；条件2、3在对近轴干涉讨论时存在矛盾，导致当x=0 时，θ ≠0，有δ ≈d sin θ ≠0，与式（1）矛盾。

文献[14-17]对光程差计算的近似条件进行了讨论，给出了代数法计算光程差的公式，对公式进行泰勒级数展开，忽略二阶小量同样得到式（1）的结论，近似条件仍为D>>d 且x>>d 。以上各种方法在光程差推导上都使用了近似，区别在于近似的时机不同，近似的精度不同，但近似的落脚点都是如何用条纹中心坐标x 的多项式来表示光程差。而在具体实验中，两束光干涉产生明条纹或暗条纹的光程差由干涉理论唯一确定。即光程差满足半波长偶数倍时，干涉加强，呈明条纹；光程差满足半波长奇数倍时，干涉减弱，呈暗条纹。实验中并不关心光程差具体是多少，更关心的是在光程差取入射光半波长的某一整数倍时，条纹中心坐标x 的具体数值。所以，关键不在于计算光程差，而在于对确定的干涉级次（即光程差确定）准确计算条纹中心坐标，考察条纹分布图样、条纹中心坐标理论值与实验值的偏差。

1 杨氏双缝干涉条纹中心坐标表达式的推导

如图1所示，由平面几何勾股定理可知：

式（2）即为两束光在P 点相遇光程差的表达式。该式在计算过程中未进行任何条件近似和修约，是两束光在P 点光程差的准确表达式。式（2）中若满足D>>d 且x>>d ，利用泰勒展开忽略平方项二次小量[18]化简可退化为式（1）。

对式（2）进行移项平方并进行同解变换，得：

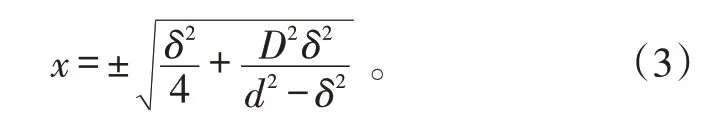
式（3）为干涉条纹中心坐标方程，也就是给定光程差所对应的干涉条纹中心坐标位置。对比式（1）和式（3），显然，只要d>10δ 时，式（3）可退化为式（1）。即杨氏双缝干涉光程差的近似计算不再须要满足文献[9-13]中所述的D>>d 、x>>d 和θ 很小的多个条件，只需满足相对弱化的条件d>>δ 即可。实际计算中，因光程差δ 常以入射光半波长的整数倍来计量（δ=kλ/2，k=0,1,2…），当入射光波长已知时，上述近似条件可以进一步转化为条纹级数d/λ>>k。

2 杨氏双缝干涉条纹中心坐标表达式讨论

物理学上，远远大于符号一般要求2 个物理量之间相差20～100 倍。实验室常用杨氏干涉光学器件一般屏距D>1m ，狭缝间距在10-1mm 量级，满足D>>d，但可观察的条纹线宽范围一般2x<10 mm，并不一定满足x>>d，只近似满足θ ≈0。文献[18]讨论了tan θ ≈sin θ 满足的条件是θ<5°。即文献[9-13]中3个近似条件不可能同时满足，经由3个近似条件得出的光程差式（1）正确性值得商榷。

由式（3）可得：

结论1：当δ=0 时，x=0，即中央明纹，与式（1）结论相同。

结论2：对于同一光程差δ，同级条纹对称分布在中央明纹两侧，且2个同级条纹到中央明纹距离相等，与式（1）结论相同。

式（3）中，由 图1 所 示 几 何 关 系，很 明 显d>a-b=δ 恒成立，对于确定的光程差，利用式（1）和式（3），分别取坐标为x1和x3，计算2种方法得出的条纹中心坐标平方差值为：

结论3：式（4）表明，当δ ≠0，即非中央明纹条件下，用式（3）计算的条纹中心坐标恒大于式（1）计算的坐标值，即实际条纹中心比式（1）计算结果靠外侧。

考察干涉加强位置（明纹），用δ=kλ 代入式（3）并对k 求导，得：

结论4：由式（5）可知，干涉条纹不等间距，将δ=(2k-1)λ/2 代入，同样可求得暗纹间距表达式，干涉暗纹间距亦不等。随着x 坐标增大，条纹间距变宽，且同级明纹间距大于暗纹间距。当干涉级次k 越大，即x 偏离主轴线越远，光程差δ 越大，在近似条件d>>λ 时，式（5）可退化为dx/dk=Dλ/d，符合经典算法中杨氏干涉条纹间距公式，可认为条纹间距相等。

式（1）和式（3）表述的条纹中心坐标相对误差记为：

式（6）利用泰勒展开，当D>>d ，d>>δ 时，即满足远场干涉条件时，忽略二级小量，可得其相对误差近似计算结果f′(δ)：

结论5：式（7）表明，当d>>δ 时，d2-δ2≈d2，利用式（1）和式（3）计算条纹中心坐标相对误差与光程差δ2成一次函数关系，曲线斜率近似为1/d2。即光程差越大，误差值越大。

取文献[3]中例2 所列数据：D=1m，d=0.2 mm，λ=500 nm，取δ=kλ，k 为干涉明纹级次。依据式（1）和式（3）分别计算不同级别明纹坐标x1和x3，利用式（6）计算其明纹坐标相对误差f(δ)，结果见表1。

由表1可见，前23级明纹似式（1）和准确式（3）计算结果误差发生在0.01 mm 位，相对误差小于0.2%；24～50级明纹近似式（1）和准确式（3）计算结果误差发生在0.1 mm 位，相对误差小于0.8%；继续计算可得在干涉级次在51～100级时，式（1）和式（3）计算结果发生在1 mm 位，相对误差不超过3.5%。

表1 干涉明纹坐标2种计算方法对比Tab.1 Comparison of two methods for calculating the coordinate of interference fringe

续表1 k x1/mm x3/mm f(δ)/% k x1/mm x3/mm f(δ)/%k891 0 k 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 x1/mm 20.0 22.5 25.0 27.5 30.0 32.5 35.0 37.5 40.0 42.5 45.0 47.5 50.0 52.5 55.0 57.5 60.0 62.5 x3/mm 20.004 22.506 25.008 27.510 30.014 32.517 35.021 37.526 40.032 42.538 45.046 47.554 50.063 52.573 55.083 57.595 60.108 62.622 f(δ)/%0.020 0.025 0.031 0.038 0.045 0.053 0.061 0.070 0.080 0.090 0.101 0.113 0.125 0.138 0.152 0.166 0.180 0.196 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 x1/mm 82.5 85.0 87.5 90.0 92.5 95.0 97.5 100.0 102.5 105.0 107.5 110.0 112.5 115.0 117.5 120.0 122.5 125.0 x3/mm 82.782 85.309 87.837 90.367 92.898 95.432 97.967 100.504 103.043 105.584 108.127 110.672 113.219 115.768 118.320 120.873 123.430 125.988 f(δ)/%0.342 0.363 0.385 0.407 0.431 0.454 0.479 0.504 0.529 0.556 0.583 0.611 0.639 0.668 0.698 0.728 0.759 0.791

3 结论

上述推导过程中，光程差并未做修约或近似。采用数学方法将光程差与坐标之间的变换式反演，解得坐标x 与光程差的准确表达式。从式（3）可以看出，条纹中心坐标近似并不需要D>>d 和x>>d 的条件，只需满足相对弱化的条件d>>δ 即可。当k 值较小时，杨氏双缝干涉准确坐标条纹分布和条纹间距与文献[3-6]中的近似算法结果一致；但在条纹级次k 较大时，条纹间距不能再认为是相等，且随着k 的增大，准确计算与近似计算误差以k2的速率增长。