基于CPHD的双层粒子滤波目标跟踪算法
李树甫,黄 勇,裴家正
(1.91049部队,山东青岛266102;2.海军航空大学,山东烟台264001)
在随机有限集的理论框架中,概率假设密度(Probability Hypothesis Density,PHD)代表多目标后验概率密度函数的一阶矩,在指定区域内的积分代表该区域目标数目的估计值[1-3]。
PHD 在应用中要求满足目标数目服从泊松分布的假设。否则,将会影响算法性能。为了应对PHD的不足,Mahler 在PHD 之上引入目标数目的势分布函数,将势分布函数定义为多目标后验概率密度函数的高阶矩[4],推导出势概率假设密度(CPHD)滤波器[5]。CPHD 未对目标数目的分布进行限定,在滤波过程中联合传递PHD 信息和势分布函数中的高阶矩信息[6],对于目标数目的估计更为稳健[7]。
PF-CPHD 算法利用粒子滤波方式进行目标状态和数目估计,不用多目标关联,是实现CPHD 的常用手段。
PF-CPHD算法应用于多目标跟踪过程中,目标状态的维数随着目标数目线性增长,需要数目相对可观的粒子数目,才能有利于解决多目标跟踪的问题[8],但粒子数量的增加在滤波过程中会额外造成粒子权重退化严重,目标数目估计不准以及计算效率下降等问题。本文通过部署双层粒子滤波,在常规CPHD滤波基础上进行改进,提出了基于势概率假设密度滤波的双层粒子滤波跟踪算法(TLPF-CPHD),考虑目标状态与邻近目标状态之间的相互影响,对当前目标状态重新计算预测,提高对目标状态的估计性能。仿真结果表明,TLPF-CPHD 算法相比于常规PF-CPHD 具有更好的目标数目和状态估计准确性。
1 基于势概率假设密度滤波的粒子滤波算法
势概率假设密度滤波除了预测和更新目标PHD,还在每一步状态预测和量测更新过程中传递目标数目的势分布函数,假定k 时刻,后验概率假设密度和后验势分布函数分别为Dk( x )和pk( n ),主要滤波步骤如下。
1.1 CPHD预测
进行概率假设密度Dk+1|k(x)的预测[9],

式(1)中:pS(ζ) 代表k+1 时刻目标的存活概率;βk+1|k(x|ζ) 表示衍生目标PHD;γk+1(x) 表示新生目标PHD。
势分布函数预测方程为:

式(2)中:pk( n′) 是k 时刻的势分布函数,n′是k 时刻代表目标数目的变量;Pbirth( n-i )表示k 时刻到k+1时刻新生n-i 个目标的概率,n 是k+1 时刻代表目标数目的变量;为组合数。
1.2 CPHD更新
同样,先进行PHD的更新运算:
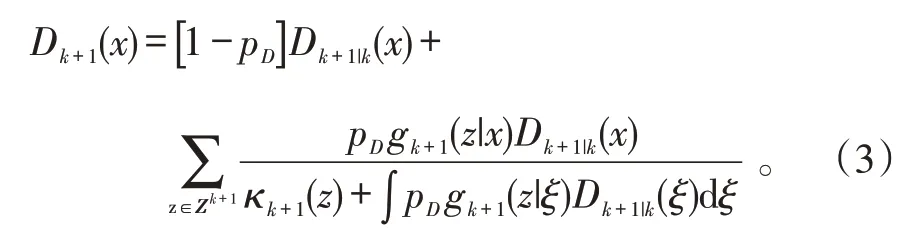
式(3)中:pD表示目标检测概率;gk+1(z|x)表示k+1 时刻目标状态的似然函数;κk+1(z)表示k+1 时刻杂波量测的PHD。
在概率假设密度滤波的基础之上再进行计算:
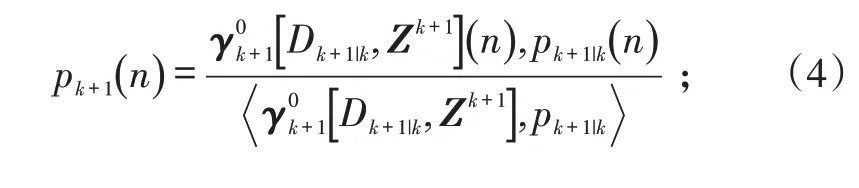
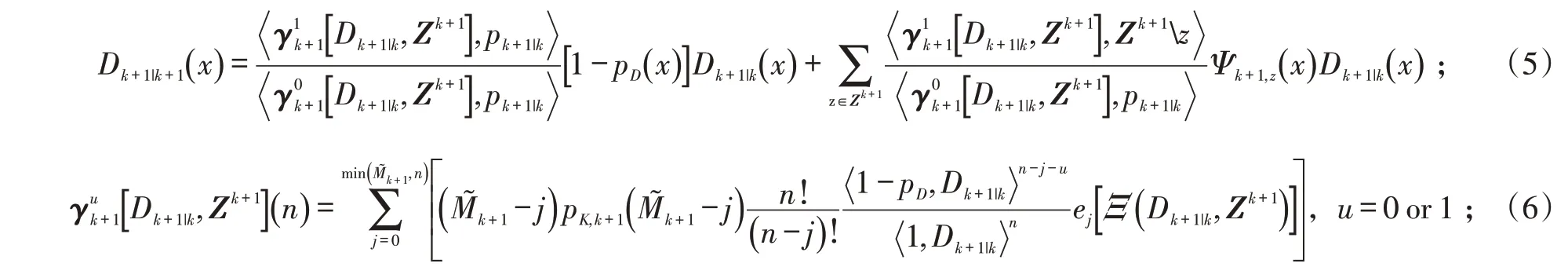
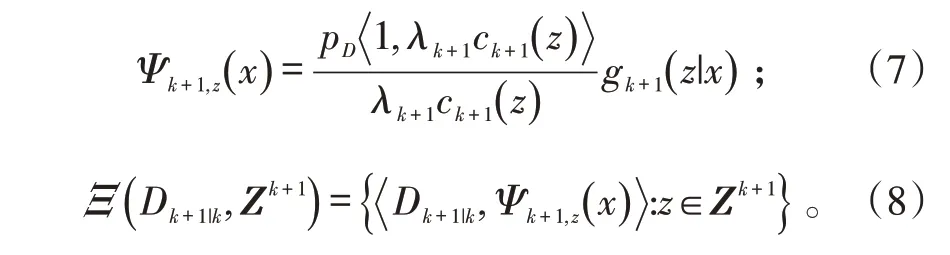
对势分布函数的更新公式为:
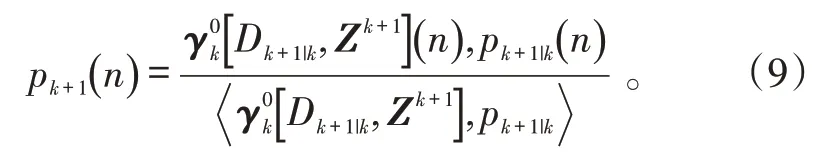
CPHD 中,对势分布函数的最大后验概率估计取整数即为该区域内期望的目标数目:
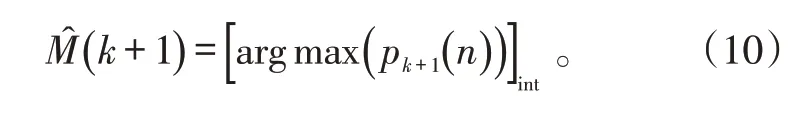
常规基于势概率假设密度的粒子滤波跟踪算法的问题是在目标数目较多时,算法需要较多的粒子数才能对多目标的概率假设密度和势分布函数具有更好的拟合,以保证对多目标状态的良好估计。但数量增加的粒子在计算中同样存在弊端,粒子在滤波过程中退化更严重,在粒子聚类时无法形成较好的聚类,使得目标数目估计不准确而且还会影响计算效率。为此,本文提出一种利用双层粒子滤波的改进方法。
2 基于势概率假设密度的双层粒子滤波跟踪算法
2.1 双层粒子设置

在粒子采样步骤中,由于考虑到周围目标的影响,得到对第m 个目标的平均预测目标状态为:
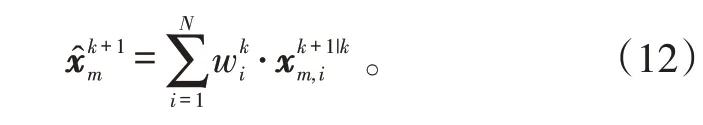
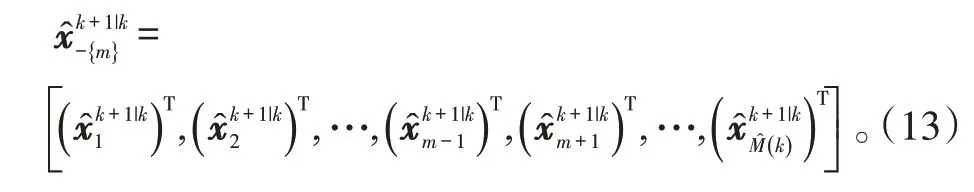
2.2 算法具体实施步骤
本文所提出的基于势概率假设密度的双层粒子滤波跟踪算法具体实施步骤如下:

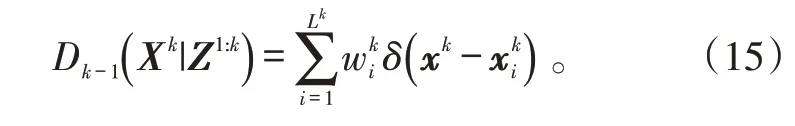
假设在k 时刻一共包括Lk个存活粒子和Jk+1个新生粒子,分别利用概率密度函数qk(⋅ |xk,Z1:k)和pk+1(⋅ |Z1:k+1)进行采样,并计算存活粒子和新生粒子的权重[16]:

预测PHD可以表示为:

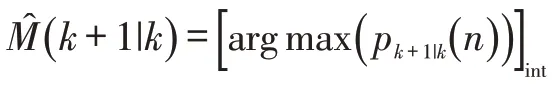

4)CPHD更新。对于k+1 时刻所有粒子的第2层粒子,根据下式更新权重[10]。
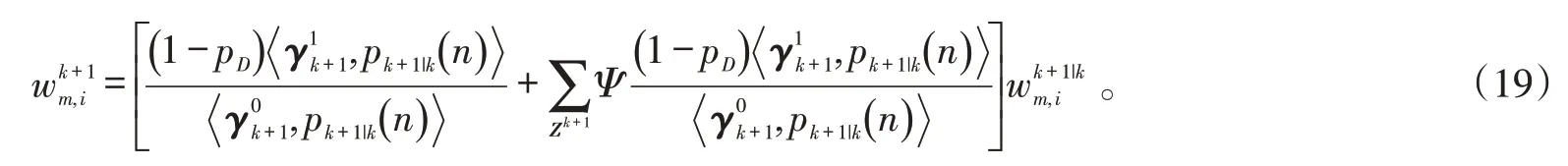
在此更新之外,还须要对第1 层粒子i=1,2,…,N进行权重更新,即进行


3 实验仿真验证
3.1 仿真场景设置

运动目标状态方程和量测方程如下:

式(21)~(25)中:F( k+1) 为系统状态矩阵;Γ( k )为过程噪声分布阵;T 为采样时间;v( k )为过程噪声;W( k+1) 为量测噪声。
表1设定了各目标初始状态及其起止时刻。由于缺乏观测区域内杂波位置分布的先验信息,本文假设各时刻剩余杂波点的位置在观测区域内均匀分布,而剩余杂波点数量服从均值为40的泊松分布,在杂波密度λc=5×10-6个/m2条件下,图1 给出了对应于表1 的真实轨迹,圆代表初始位置,三角代表终止位置。
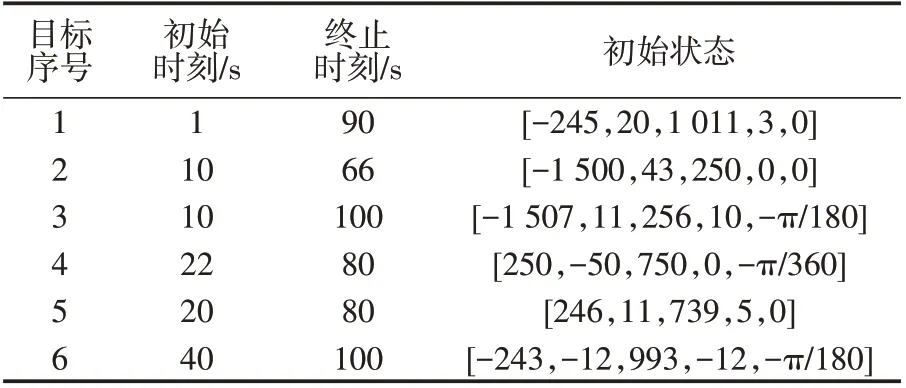
表1 各目标初始状态及其起止时刻Tab.1 Initial state of targets and their start and end time

图1 各目标的真实运动航迹Fig.1 True trajections of all targets
3.2 算法性能对比
进行100次Monte Carlo仿真实验,每一次都对算法所估计的目标数目进行记录,求取平均值。通过综合分析图2的跟踪效果和图3的多目标跟踪数目估计结果得出,二者都对目标数目做出了较为准确的估计,但在多目标数目发生波动时,TLPF-CPHD算法要比PF-CPHD算法更为敏感,能够在目标数目变化时更加及时地确定多目标数目。另外,在仿真过程中,PFCPHD 算法对目标数目估计有一定程度的过估计,跟踪位置准确性也欠佳。

图2 2种算法的跟踪效果Fig.2 Tracking effect of two algorithms
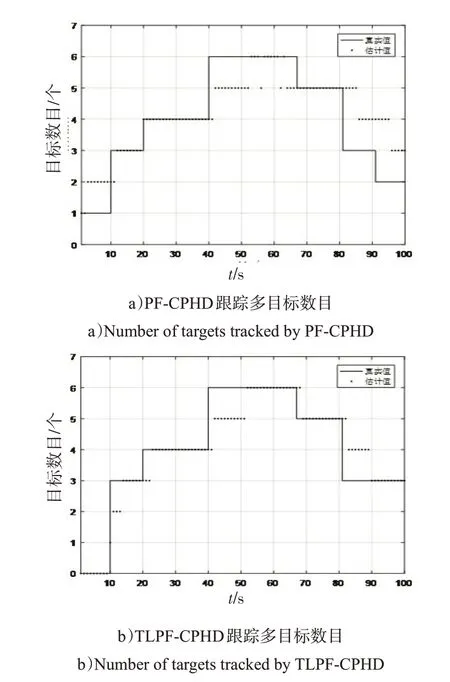
图3 2种算法的多目标跟踪数目对比Fig.3 Comparision of the number of multi-target tracking of the two algorithms
进行100次Monte Carlo仿真实验,每一次都对最优子模式分配(OSPA)距离误差进行记录求取平均值。OSPA距离为目标数目估计的误差与目标位置估计的误差之和[18]。本文设置OSPA误差指标中的截断距离c=100 m,距离参数p=1,将整个过程中每一步的100次OSPA误差进行算术平均,得到图4关于目标状态估计的OSPA距离误差统计。从整个跟踪的过程来看,TLPF-CPHD算法要比PF-CPHD算法更为稳定,其总的OSPA 距离误差更小,说明对多目标的状态和数目的总估计更为准确可靠。

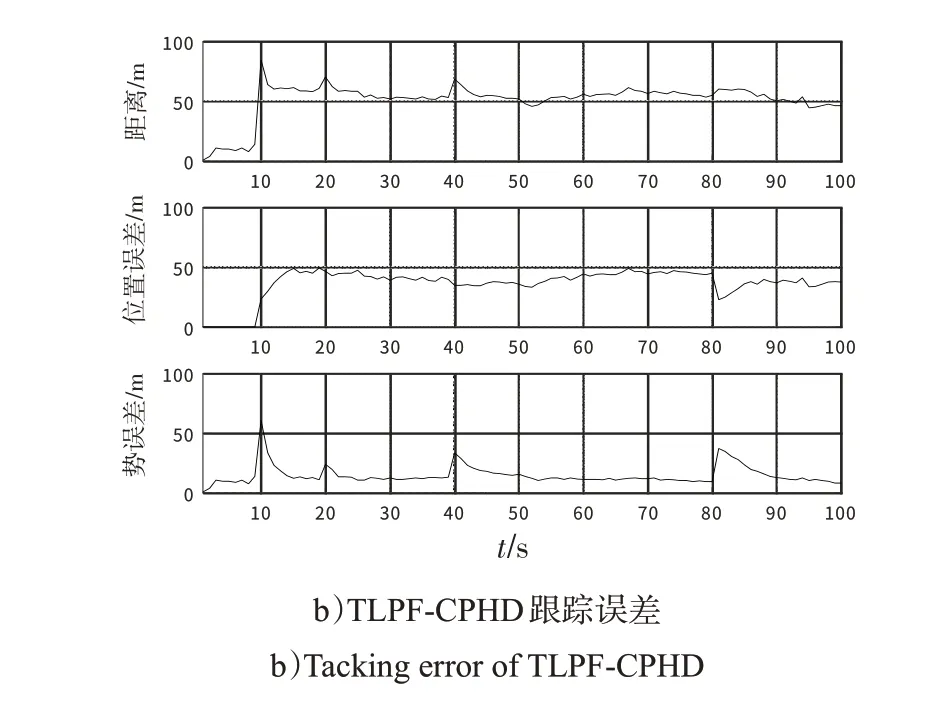
图4 2种算法的跟踪误差对比Fig.4 Comparision of tracking error of the two algorithms
4 结论
本文针对常规基于势概率假设密度滤波的粒子滤波跟踪算法在多目标跟踪应用中需要粒子数目较多,粒子权重退化较为严重带来运算效率下降,目标数目估计不准等问题,为了弥补单纯增加粒子数量而带来的缺陷,部署双层粒子,提高粒子的利用率。仿真实验表明,TLPF-CPHD 算法的跟踪效果优于PFCPHD。虽有改进,但缺点还是不可避免地较常规算法具有额外的运算负担。下一步的研究重点包括解决在保证准确性的前提下尽量降低计算复杂度,以及利用实测数据对算法性能进行验证。

