突发事件冲击下基于或有支付机制的创投融资决策*
赵林梦,胡支军
(贵州大学 数学与统计学院,贵州 贵阳 550025)
1 引 言
全球经济发展的实践表明, 创新型中小企业是经济发展的重要推动力量.风险投资作为一种主要以高科技、高风险的创新型项目为投资目标的资本形式, 在帮助创业企业解决融资难等问题上发挥着重要的作用.就创业企业而言,其投资项目的价值除了受市场不确定性的影响外,还会受到突发事件,如自然灾害、瘟疫、金融危机、新竞争者的加入等的冲击.这些突发事件会导致项目的价值发生离散的跳跃.如何测度这些不确定性与特定的跳跃风险对创业企业的价值以及投资阈值的影响,是评估创业投资时的一个重要课题.
从金融学角度看,创业企业融资决策通常涉及对创业企业的估值,创业企业家(EN)和风险投资家(VC)如何分割企业所有权也是其中的相关问题.考虑到创业企业前景的不确定性,EN和VC可以选择通过预付股权或现金溢价,或者根据企业的业绩基准设置一个或有支付机制(Contingent Payment Mechanism,CPM)来解决关于项目估值和企业所有权的问题.或有支付机制(CPM),文献中也称为或有Earn-outs, 是在并购交易中买卖双方为解决估值分歧,依据标的资产未来业绩等条件的达标程度来调整支付款项的一项合约安排.在这种支付安排下,并购双方通过将传统的一次性支付转变为延期支付的模式,以解决双方的估值分歧.
目前关于创业融资决策或者在并购(M&A)环境下涉及CPMs的决策模型的文献并不多见.Datar等(2001)[1]指出,CPM是一种收购方法,其中卖方收到的最终对价是基于其业务的未来表现.Lukas等(2012)[2]对CPMs采用两阶段期权博弈方法,以考察不确定性和或有支付条款对最佳并购时机的影响.Barbopoulos和Sudarsanam(2012)[3]指出CPM可能出现在“媒体和娱乐”、“消费品”、“高科技”、“医疗”和“电信”等行业.Lukas和Heimann(2014)[4]通过一个具有信息不对称特征的并购环境下的理论模型,推导出了一系列关于或有支付机制的可检验的经验命题.Choi(2016)[5]针对并购背景建立了一个两阶段博弈模型,目的是解决交易后期如何影响最优或有支付机制的设计问题.谢蔼莹(2018)[6]针对信息不对称和未来不确定性带来较大风险的问题,结合相关并购案例研究或有支付可能产生的正面和负面效应.Tavares-Gärtner等(2018)[7]设计了一种实物期权方法对所确定的四种主要不同的CPM进行估值,并展示了如何最优地设计这些不同的CPM,以便在EN和VC之间不会产生利益冲突的情况下,最好地支持创业企业的成长战略.
随机过程选择在实物期权估值中起着核心作用,它不仅会影响项目价值,还会影响投资规则.以往关于创业投资的研究大都是假设项目的投资价值为连续(扩散)随机过程,投资期间没有考虑突发事件发生的可能性.例如,Berk等(2004)[8]将未来现金流量风险分成系统风险与技术的特定风险来评估创投的价值与风险溢酬.阳军等(2012)[9]假设产品需求服从几何布朗运动,应用实物期权理论方法推导出不变产出和可变产出条件下企业最优投资时机和投资规模的解析表达式.Lukas等(2016)[10]假设项目价值服从几何布朗运动,基于 EN和VC之间的期权执行博弈提出一个创业融资的动态模型,分析了多阶段融资以及经济和技术不确定性对最优合约的影响.Tavares-Gärtner等(2018)[7]假设创业企业的利润流服从连续的几何布朗运动,证明了最优投资时机与CPM的选择无关.Tavares-Gärtner等(2018)[11]基于EN和VC对创业企业的成长前景持有相同和不同的观点,建立了一个实物期权模型来确定促使EN和VC同时对创业企业行使增长期权的最优股权结构.Chang等(2020)[12]研究了创业企业的项目价值存在多种可能的概率分布且EN和VC对项目付出的努力具有互补效应时的风险投资最优合约设计问题.
随着社会、经济、环境等领域的系统复杂性日益增加,创业企业投资项目的价值除了受不确定性的影响外,还会受到金融危机、自然灾害、重大疫情或新竞争者的加入等突发事件的冲击(穆庆榜(2016)[13]),导致项目价值运动的随机过程呈现出不规则的离散跳跃,几何布朗运动等连续型随机过程并不能完全刻画项目价值的真实变化情况.因此很有必要在分析中引入“泊松(Poisson)跳跃”过程来模拟这种由突发事件所导致的价值跳跃,更加真实地描述投资项目价值变化的随机过程,进而克服基于几何布朗运动等扩散过程的投融资决策的不足.
针对现有基于CPM的创业融资决策模型的不足,拓展Tavares-Gärtner等(2018)[7]的研究,假设创业企业的利润流服从带Poisson跳跃的几何布朗运动,应用实物期权方法研究突发事件影响下创业企业的最优融资决策问题,设计最优的或有支付机制就很有必要了.
2 突发事件影响下基于CPM的创业企业融资决策实物期权模型
Tavares-Gärtner等(2018)[7]假设创业企业的利润流服从几何布朗运动扩散过程,考察了作为创业企业融资决策的一种资本筹集策略CPM.Dixit和Pindyck(1994)[14]指出,带有离散跳跃的几何布朗运动模型很适合模拟企业的现金流.例如,一家企业的收益会受到一些不可预测但相当大的变化的影响,这些变化是对好消息或坏消息的反应.因此,不同于文献[7]的模型,在描述包含突发事件的现实不确定性时,将其设定为带“跳跃”的几何布朗运动.本节首先建立刻画突发事件影响下的企业利润流的跳跃-扩散模型,然后推导出EN和VC持有的企业成长机会的期权价值,为研究CPM如何影响其结果做好基础性工作.
2.1 变量描述与模型建立
考虑一家由一个EN拥有的创业企业,通过扩大当前的利润流(用eEXP>1表示)和给定的资本支出(用k> 0表示),使企业产生正的利润并保持成长机会.假设EN和创业企业都无法获得债务融资,这种资本支出应当通过由拥有有限资源的EN和外部融资人支持的一轮股权融资来提供资金,而外部融资人被认为是一个不受资金限制的VC.假设VC可以提供EN所需的部分资金.
使用以下符号表示相关的变量:
ki表示EN提供给创业企业的初始资本,
ka表示EN愿意向创业企业投入的额外资本,
k表示创业企业执行成长战略所需的资本支出总额,
(k-ka)是VC投入创业企业的资本.
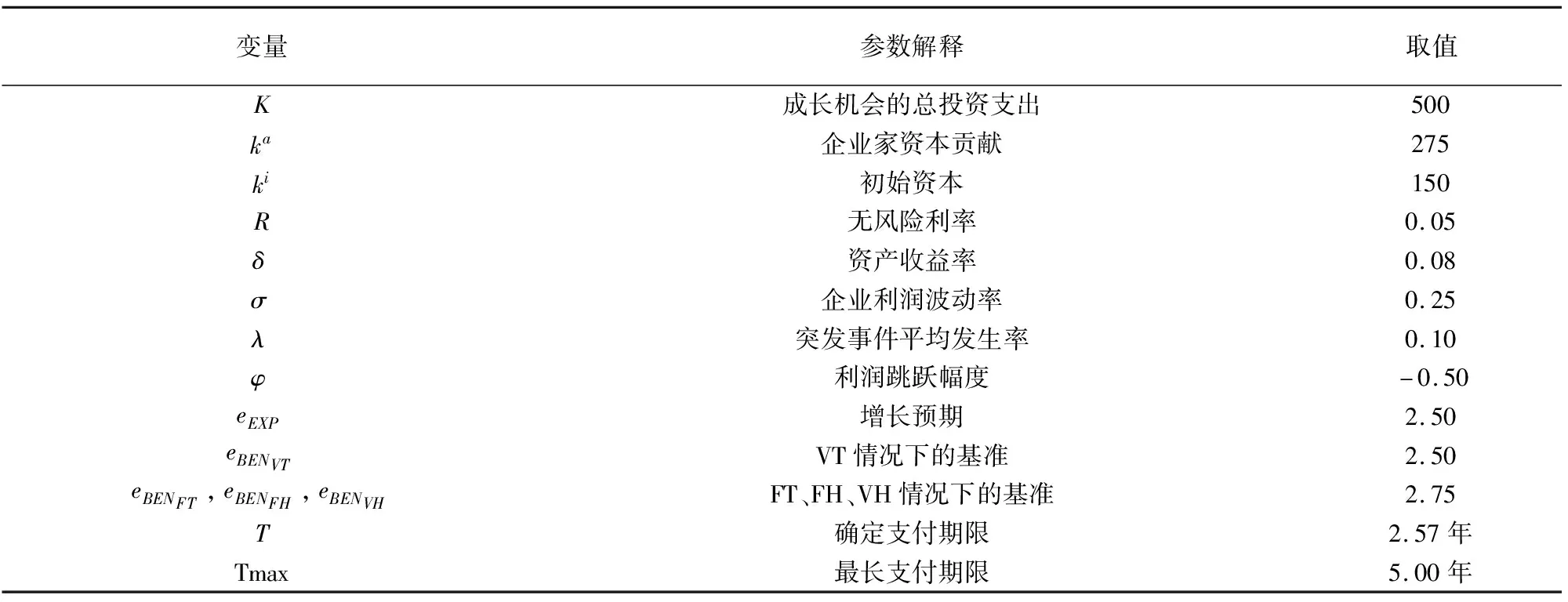
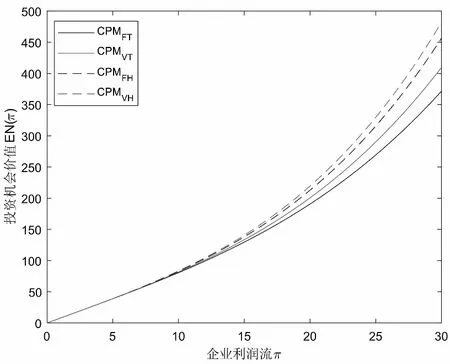
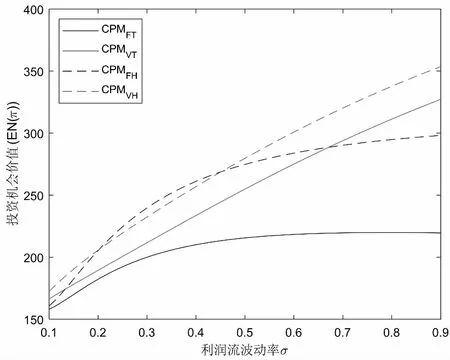
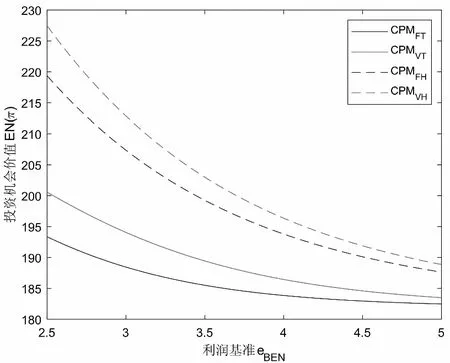
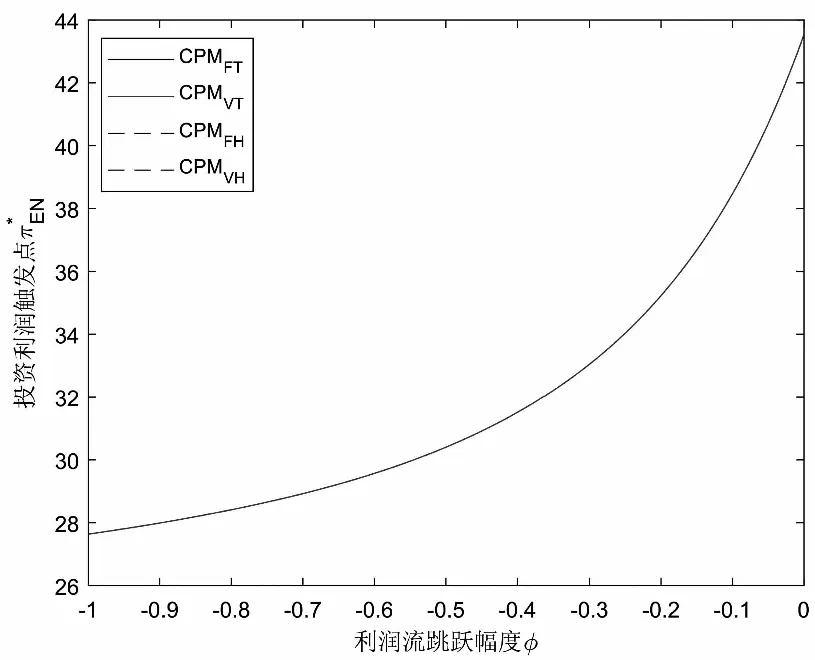
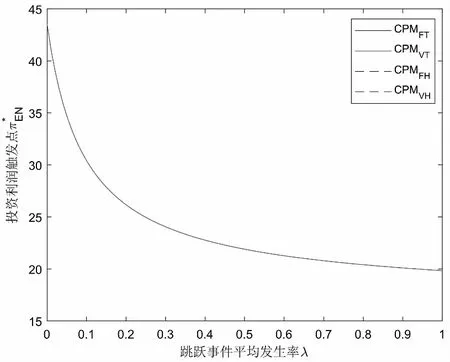
假定双方在进行某轮股权融资后根据各自对创业企业的出资额来决定其对企业的所有权.经股权融资后EN持有的股权表示为0 创业企业的项目价值(或利润)受外部市场环境及其经营状况的影响.假设项目产生连续时间利润流(t),服从带Poisson跳跃的混合布朗运动 dπ=απdt+σπdz+φπdq (1) 其中α和σ分别为漂移参数和瞬时波动率参数. 在风险中性条件下,α=r-δ,r>0是无风险利率,δ>0是资产收益率,从而α为风险中性下的漂移,dz是标准维纳过程的增量.dq为突发事件变化过程服从平均到达(发生)率为的Poisson过程的增量,并且dz和dq相互独立,即E(dzdq)=0.因此,dq=0的概率为1-λdt,而dq=1的概率为λdt,换句话说,在充分短的时间区间dt内,项目价值π发生跳跃的概率是λdt.φ 表示跳跃的幅度,满足-1≤ φ≤0,其中负号表示向下跳跃,模型(1)也称为跳跃-扩散过程.最后,假定EN和VC认为项目价值(t)服从相同的随机过程,即EN和VC对项目的价值具有同质信念. 如式(1)所示,在企业利润流的动态过程中加入的一个跳跃成分,用来描述突发事件对企业利润流的影响.这种企业盈利的一般设置使得能够在更符合实际经济环境的情景下研究创业企业的融资决策,得到比Tavares-Gärtner等(2018)[7]报告的更为稳健的结果. 根据Dixit和Pindyck(1994)[14]的或有权益分析方法,EN持有的投资于创业企业成长机会的期权价值EN()满足式(2)所示的常微分方程. (2) 上式左边最后一项为创业企业的当前利润流,而其余的项表示创业企业持有的增长期权.假设EN(0)=0,则方程(2)的解的一般形式为 (3) 其中A是待定常数,是式(4)所示非线性方程的根. (4) (5) (6) 条件(5)表示EN决定投资成长机会时获得的收益.条件(6)保证了EN()在>0连续可微. (7) 考虑到VC(0)=0,方程(7)的解的一般形式为 试验组45(100.00)的满意度对比对照组满意程度35(77.78)更高,差异有统计学意义(P<0.05)。 VC(π)=Bπβ, (8) 其中B为待定常数,为非线性方程(4)的正根.相应的边界条件为 (9) (10) 本节讨论求解使得EN和VC愿意共同支持创业企业成长机会的利润触发点和最优或有支付.研究发现,EN和VC持有的投资期权的价值和利润触发值均与刻画突发事件的两个参数和有关. 类似于Tavares-Gärtner等(2018)[7]的方法,将CPM视为二元式看涨期权,而不是股票的普通看涨期权,因为它们的回报实际上是不连续的,即要么是固定金额,要么是线性依赖于标的资产价值的可变金额.因此可以把固定数额的CPM定义为现金或空手看涨二元式期权,如果创业企业达到或超过给定的绩效基准,EN应当获得固定数额的现金. 当CPM是按确定的期限到期时,或有支付可以被建模为传统的二元式期权[15].对于按期到期的或有支付,假设该期限是由双方共同决定的,并由t >0给出. 当或有支付是当企业业绩达到基准业绩时到期,或有支付应当被建模为二元式障碍期权[16]. 根据上述分析,支付日期为确定期限的固定数额或有支付(记为CPMFT)可以被建模为现金或空手看涨期权,其价值如式(11)所示. CPMFT=θFTe-rtN(d2FT), (11) 其中 (12) 其中 (13) 类似地,通过联立求解方程(9)、(10)和(11)可以推导出在CPMFT下,VC持有的投资于成长机会的期权价值和利润触发点为 其中 (14) (15) (16) 不难发现,当λ=0或φ=0,即不考虑突发事件对项目价值的影响时,式(15)与式(16)相同. 这种类型的CPM可以被视为资产或空手看涨期权,如式(17)所示. CPMVT=mVTπ(eEXP-1)e-δtN(d1VT), (17) 其中 通过联立求解方程(5)、(6)、(17)可以获得EN投资于成长机会的期权价值,而通过联立求解方程(9)、(10)、(17)则可以获得VC投资于成长机会的期权价值,以及双方各自的最优利润触发值,如下式所示. 其中 (18) 并且 其中 (19) (20) 根据Rubinstein和Reiner(1991)[17],假定触发或有支付的业绩基准大于或等于其当前水平,到期日为目标实现时刻且支付固定数额的或有支付(记为CPMFH)可以被看作向上敲入现金或空手看涨二元式障碍期权,其价值如式(21)所示. (21) 其中 (22) (23) (24) 其中 (25) 以及 其中 (26) (27) 对于在达到业绩基准时(at hit)到期并支付变动数额的或有支付机制(记为CPMVH),假设业绩基准大于或等于其当前水平,可以将这种类型的CPM视为向上敲入资产或空手看涨二元式障碍期权.采用类似于Tavares-Grtner等(2018)[7]的方法,得到其价值如式(28)所示. (28) 其中a,b和z分别由式(22)、式(23)和式(24)定义.进一步,由式(5)、式(6)、式(28)和式(9)、式(10)、式(28)可求得EN和VC投资成长机会的期权价值和他们的最优投资利润触发值分别为 其中 (29) 以及 其中 (30) (31) (32) (33) (34) (35) 从中不难发现,对每一种CPM类型,由于EN和VC的最优投资时机具有关于刻画突发事件的两个参数和的相同的表达式,因此,在考虑突发事件的影响时,双方共同投资的最优时机仍与CPM的类型无关. 下面考虑双方共同投资时或有支付的价值,用CPMF表示固定数额或有支付,通过联立求解式(3)、式(5)和式(6),可以获得EN投资于企业成长机会的利润触发值为 同样,通过联立求解式(8)、式(9)和式(10),得到VC投资企业成长机会的利润触发值为 (36) (37) 总的来说,或有支付对于EN表示其持有的关于投资成长机会的期权的资产,对于VC则表示其持有的关于投资成长机会的期权的同等负债,当控制影响可变或有支付的随机参数时,最优投资时机不受或有支付机制设计的影响.但是,在考虑突发事件的情况下,不同类型的最优或有支付均受Poisson跳跃过程的参数的影响. 接下来,将通过数值分析来说明本节获得的解析结果背后的经济意义,并讨论突发事件的两个参数对最优投资时机的影响. 本节通过一个数值例子来说明突发事件影响下基于或有支付的融资决策的相关结论.利用MATLAB软件进行数值模拟,给出最优或有支付和最优投资时机.分别研究当前利润流、利润流波动率、业绩基准对投资机会价值的影响,以及突发事件的跳跃幅度(或影响规模)和平均发生率对最优投资时机的影响. 借鉴相关文献设定影响创业企业投资期权价值及其标的利润触发点的参数[7,9,14],相关参数的具体取值见表1.根据式(4)可求得的数值解,同时,经计算可得QEN=65.4%以及QVC=34.6%. 表1 参数设置 表2给出了在考虑突发事件的影响下,当创业企业的利润流服从式(1)的跳跃-扩散过程时,根据第3节中的理论结果计算得到的相应最优固定数额或有支付*、最优可变数额或有支付m*以及最优利润触发点π*. 表2 最优CPM 表2的数值结果显示,当企业利润流服从跳跃-扩散过程,且双方同意业绩基准在短期内可达到时,确定期限支付的CPM比业绩基准实现时刻支付的CPM产生更高的支付数额或支付倍数.最后一列数据显示,最优决策时投资时机与或有支付机制的类型无关,这验证了3.5节的结论. 不同的或有支付机制价值不同,其潜在的投资机会价值也不同,表2的结果也验证了这一点.对于固定数额CPM,支付日期分别为固定期限和业绩目标实现时刻,会支付不同的数额.对于可变数额CPM,在确定期限和业绩目标实现时刻支付的CPM,其支付倍数也是不同的.下面从EN的角度分析主要参数对投资机会价值和最优投资时机的影响. 4.2.1 当前利润流和投资机会价值 假设m=4.0,=150,图1说明了EN在π<π*范围内所拥有的投资机会的价值的直观含义.其中,虚线表示在固定期限支付的或有支付机制,而实线则表示在目标实现时刻支付的或有支付机制. 图1 企业利润流与EN持有的投资机会的价值 可变金额CPM比固定金额CPM更有价值,因为可变数额CPM可能产生正的支付或更低的盈利水平,并且当盈利能力超过其基本阈值时,可能产生比固定金额CPM更高的收益. 4.2.2 利润流波动率和投资机会价值 本节讨论利润流波动率如何影响每一种或有支付机制下投资成长机会的期权的价值.假设m=4.0,=150,0=20. 图2表明,利润流的变化遵循跳跃扩散模型的情况下,波动性增加会给投资机会带来额外的价值,并且可变或有支付对利润流波动率的变化更敏感.对于可变数额或有支付,波动率越高投资机会价值越大,表明波动率较高的企业更应该选择可变或有支付,而对于固定数额或有支付,较高水平的波动性下的投资机会价值趋于稳定. 图2 利润流波动率与EN持有的投资机会的价值 4.2.3 业绩基准和投资机会价值 由于业绩基准影响获得或有支付的可能性,因此预期二者之间会出现负相关关系.假设m=4.0,=150,0=20.对一系列高于预期利润增长的业绩基准(即eBEN>eEXP),图3显示了EN持有的投资于成长机会的期权价值之间的关系. 图3 业绩基准与EN持有的投资机会的价值 双方约定的基准越高,EN实际获得或有支付的可能性就越低,亦即其投资机会的价值越低. 4.2.4 利润流跳跃幅度和最优投资时机 针对四种类型的CPM,考察Poisson跳跃过程的跳跃幅度参数对 EN投资的最优利润触发点(最优投资时机)的影响.假设m=4.0,=150,0=20.图4显示了EN投资的利润触发点与跳跃幅度的关系.跳跃幅度越大,利润触发点越小(负号表示利润流跳跃方向,即向下).较大意味着投资机会的价值较小(利润流将会下降较大的比例),立即投资的机会成本较小,因此,跳跃幅度越大,EN更倾向立即投资而不是等待. 图4 跳跃幅度与投资时机 4.2.5 事件平均发生率和最优投资时机 图5 事件发生率与投资时机 引入Poisson跳跃过程描述突发事件的发生导致企业的利润流出现的离散跳跃,应用实物期权方法通过数理推导给出了四种不同类型或有支付下的最优或有支付数额表达式与最优投资时机. 研究发现,考虑突发事件的影响时,双方同时投资的最优时机与或有支付机制的类型选择无关.数值分析结果表明,在业绩基准实现时刻支付的或有支付比在确定期限支付的或有支付具有更高的价值,可变数额或有支付比固定数额或有支付具有更高的投资机会价值.波动率越高投资机会价值越大,对于固定数额或有支付,较高水平的波动性下投资机会价值趋于稳定.突发事件的平均发生率越大,双方共同投资的时机越早.利润流跳跃幅度越大,共同投资的时机也越早. 研究结果可以帮助提高创业企业家和风险投资家之间达成协议的可能性,促进创业企业顺利融资.但是对现实情况的考虑还可以更加深入一些.创业企业家和风险投资家对创业企业的利润增长有不同预期,突发事件对利润流的影响为随机影响等,可以进一步展开系统深入的研究.2.2 企业家持有CPM的期权价值
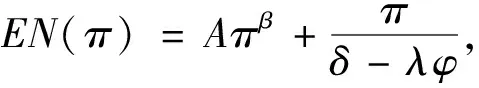
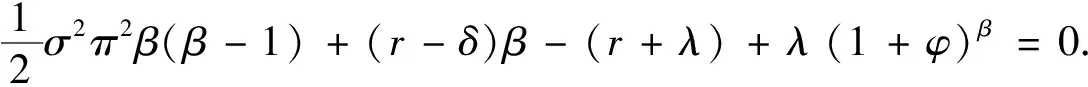
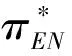
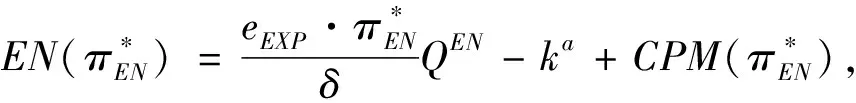
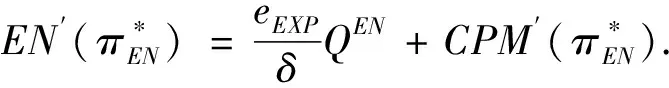
2.3 风险投资家持有CPM的期权价值
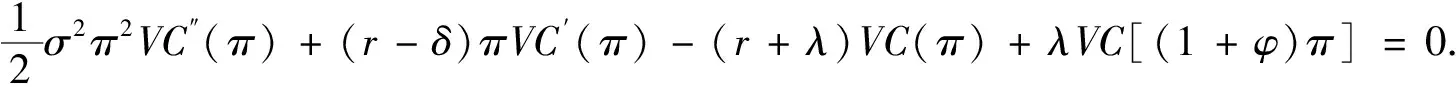
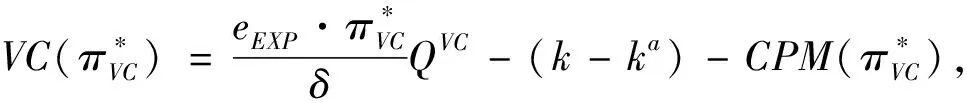
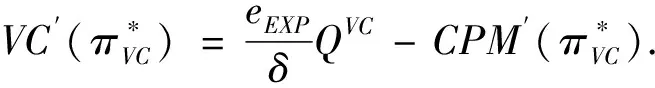

3 突发事件影响下四种CPM类型的创业企业最优融资策略
3.1 基于确定期限支付固定数额CPM的融资策略

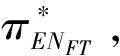
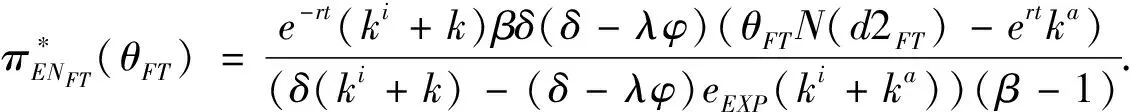
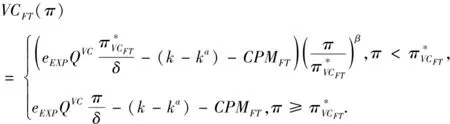
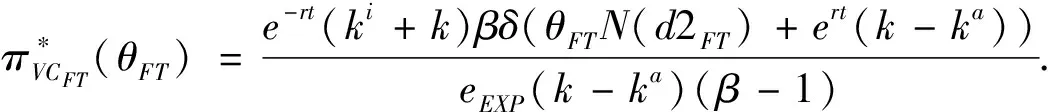
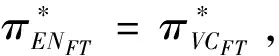
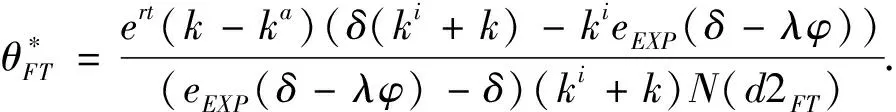
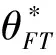
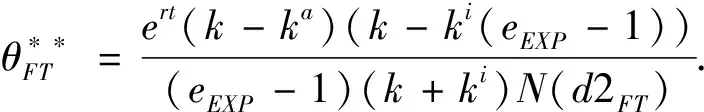
3.2 基于确定期限支付可变数额CPM的融资策略

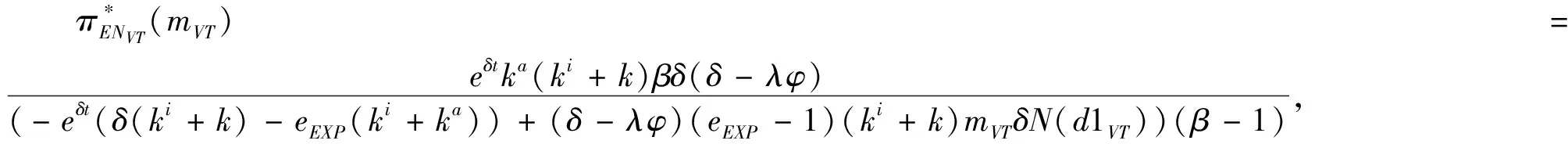
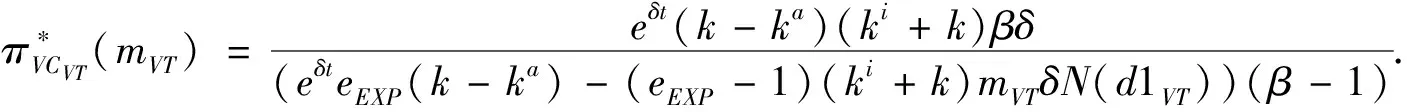
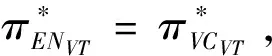
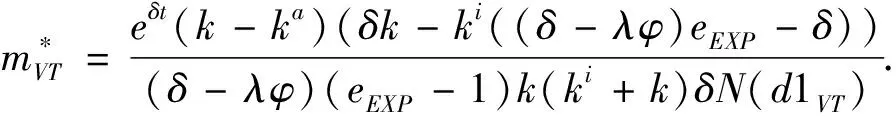
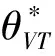
3.3 基于目标实现时刻支付固定数额CPM的融资策略
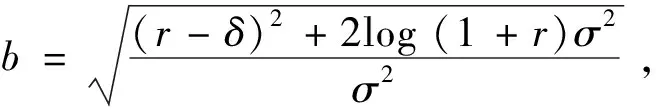
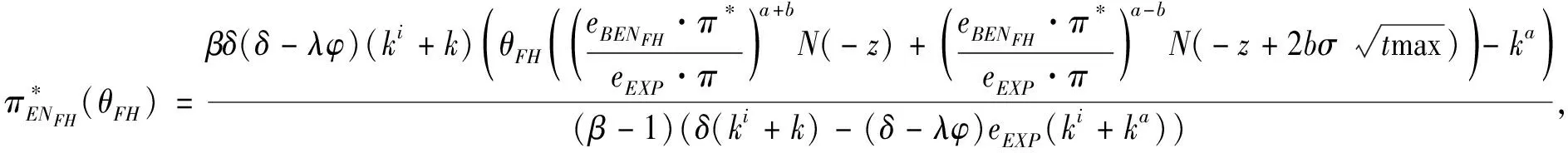
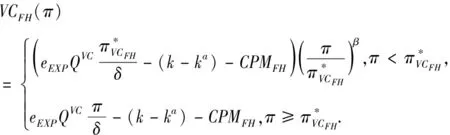
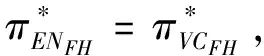
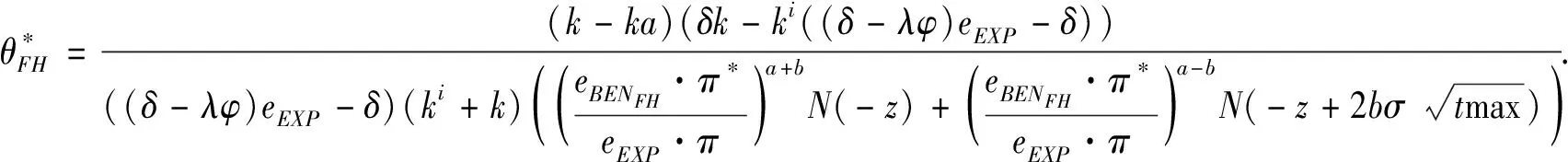
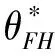
3.4 基于目标实现时刻支付可变数额CPM的融资策略

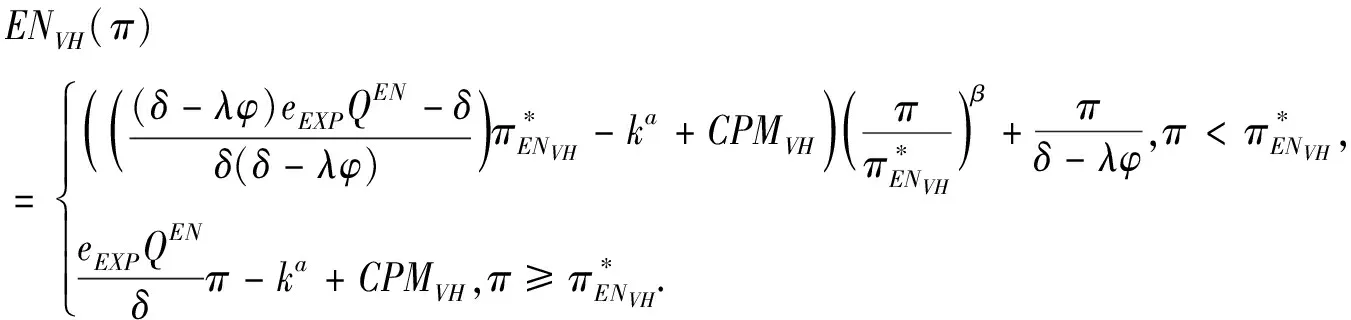
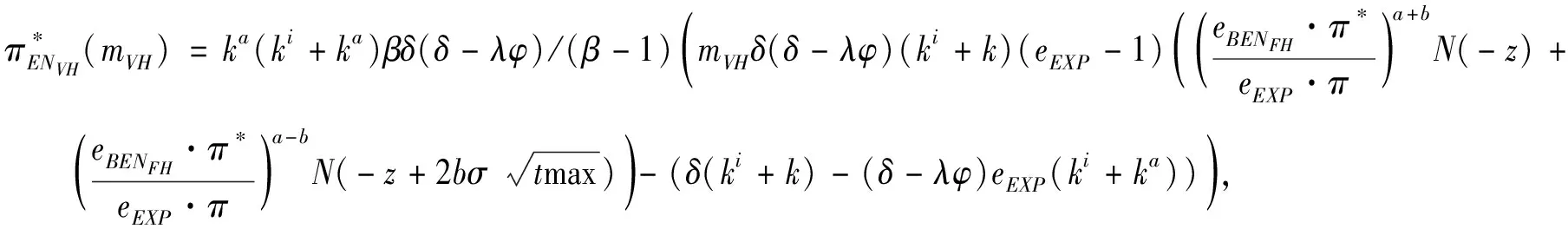
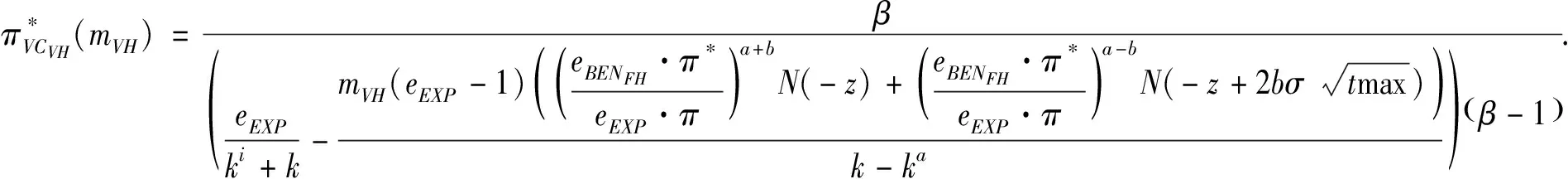
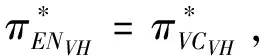
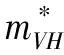
3.5 CPM与最优投资时机
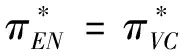
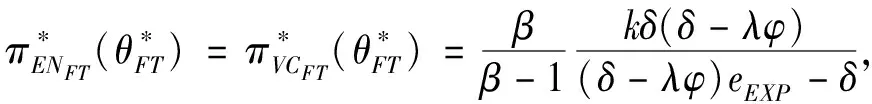
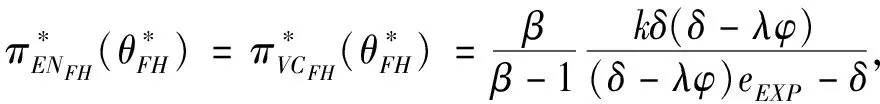
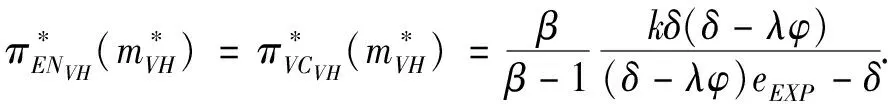
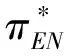
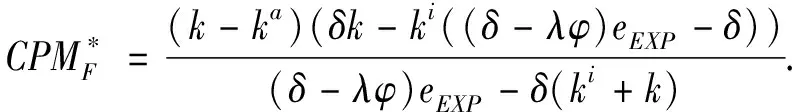
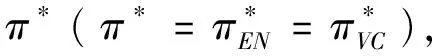
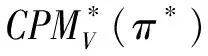
4 数值模拟及敏感性分析
4.1 参数设置
4.2 结果分析

5 结 论

