雷达最大探测范围可视化

王欣，赵兀君，李辉

（1.四川大学计算机学院，成都 610065；2.海军装备部，南昌 333000）

0 引言

电磁活动在人们的生活中随处可见又是“不可见”的。在军事方面，数量巨大、功能各异且分工明确的电磁设备扮演着重要角色，坚守在自己的“岗位”上。雷达用于战场信息的探测、是武器系统的重要组成部分，它是重要的传感装置，能够检测到远距离外的超出人们视力范围的事物，并且通过数据反映出来。但是这些数据相对来说还是比较抽象，难以让人在第一时间把握总体态势，而对空间中的电磁环境准确认识又恰恰是决策的根本条件之一。那么将抽象的数据或是二维的图形进行三维的显示，能够更加直观，对于理解当前的情况更加友好。

关于雷达探测范围的问题自有雷达以来就一直在被人们所讨论，也是衡量雷达性能的重要指标。自由空间下的计算有Kerr 提出的距离公式，利用信噪比等因子进行理想化的计算。评估电波传播特性有抛物方程法，可以分析地表起伏、电磁特性变化及大气折射率变化等条件下的电波传播问题[1]。对于雷达的各种衰减因素也有很多方法进行分析，例如对于大气影响，可以用等效地球半径方法仍然将电磁波传播路径作为直线来处理有关大气折射的问题；氧气和水蒸气吸收衰减方面有Libebe 和ITU-R 模型，以及利用双线性内插法计算水平-垂直非均匀大气折射剖面等[1]。对于雷达探测概率的计算有Marcum 和Swerling 模型和概率融合公式。

1 雷达探测范围

雷达是一种用于探测和定位反射目标的电磁传感器。雷达诞生初期多是为军事需要提供服务，可以监视海陆空、完成侦查任务、实现精准打击、导航等。今天军队仍然是雷达的主要用户和雷达技术的主要开发者[2]。

雷达通过发射电磁波并接收目标物体反射回来的电磁波后对信号进行的解析处理来得到有关目标的信息。雷达结构可以概括为发射机、天线（如果是单基地雷达只有一根天线）、回波接收机、信号处理机以及显示器这几个主要部分。对于不同的功能需求和应用目的可能还有抗干扰等辅助设备。

1.1 雷达距离方程

（1）雷达探测范围概述

①雷达距离方程

雷达距离方程包含了许多关于雷达系统的以及雷达所处环境的参数。下列方程是由Kerr 提出，在自由空间下成立的雷达公式（我们这里表示的自由空间指的是除了雷达以及目标外，以雷达为中心并延伸到远远超出目标范围以外的球形区域是空的，是一种理想条件）：

其中的参数表示为：

Pr 表示（天线终端处）接收信号功率，Pt 表示（天线终端处）发射信号功率，Gt 表示发射天线功率增益，Gr表示接收天线功率增益，σ表示雷达目标截面积，λ表示波长，Ft 表示发射天线到目标路径的模式传播因子，Fr 表示接收天线到目标路径的模式传播因子，R 表示雷达到目标之间的距[3]。方程中的Ft 表示的是目标处的实际电场值和自由空间理想条件下距雷达相同距离处沿着天线波束的最大增益方向的电场强度E0 的比值，包含天线方向图因子以及各种影响因素（如大气、地形等）。这里的方程针对单基站雷达，雷达的发射天线和接收天线相同，因此与之相关的参数中Gt、Gr 相等，Ft、Fr 相等，方程可以写成下列形式：

变换方程，可知如果可以得到Pr的最小值，也就是Prmin，我们能够计算出最大的距离值Rmax。

根据资料知，Pr与Pt的比值与信噪比相关。

信噪比的值为设备或系统接收并处理的来自外部的信号与接收设备产生的噪声信号的比值。

在这里（雷达系统中）信噪比可以表示为：

Pn表示的是接收机噪声功率的电平。Pn与接收系统的噪声温度Ts相关：

这里的k 是Boltzmann 常数，Bn表示接收机预检测滤波器的噪声带宽，Ts以开尔文为单位，一般取值为290K。由此可得：

引入系统总损耗L，最后的最大距离公式如下：

②雷达方向图因子

天线具有方向性。通过在空间坐标上的电场强度与空间方向的三维关系图可以描述天线的方向性。根据不同的方向图特点，我们可以把雷达分为全向雷达，高斯型雷达，SIN（X）∕X 型雷达等。不同辐射水平下的最大天线辐射强度，可以用方向图因子来描述。

对于高斯型雷达，它的方向图函数为：

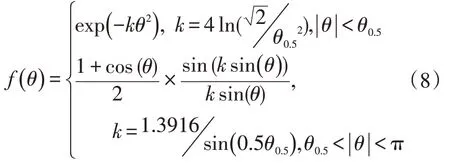
其中的θ表示目标在垂直方向上偏离雷达天线主轴的角度，θ0.5表示雷达主瓣宽度[4]。

对于 SIN（X）∕X 型雷达，它的天线方向图函数为[4]：

其中ΔA=θ-Aelev，这里的Aelev指的是雷达天线仰角这里的bw 与前文的θ都指的是雷0.5达波束宽度（beamwidth）。Amax是雷达主瓣的最大角度，

（2）雷达探测范围模型

建模时，我们使用结构体保存雷达系统的相关参数。之后将空间分层，每个水平层根据设定的步长和步数计算顶点坐标，其排布为圆形。同时在垂直方向，也通过设定步长和步数，计算完一个水平层后进行下一个水平层顶点的计算。这里我们需要根据一定的顺序排布顶点，使之有一定的规则性，组合成面元，形成整个包络面。在使用三角形面元（Triangle_strip）的情况下，需要交错求出上下两层顶点。构造包络的流程如下：

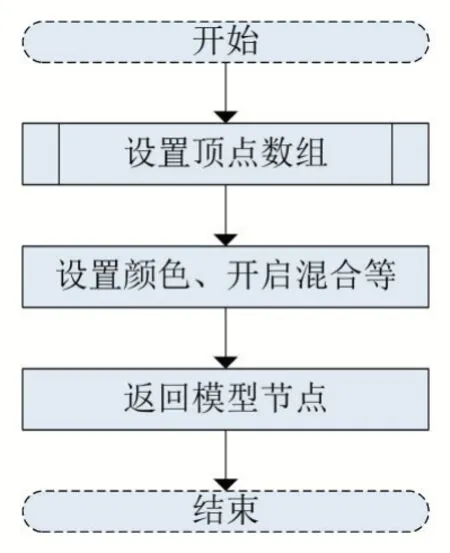
图1 总流程

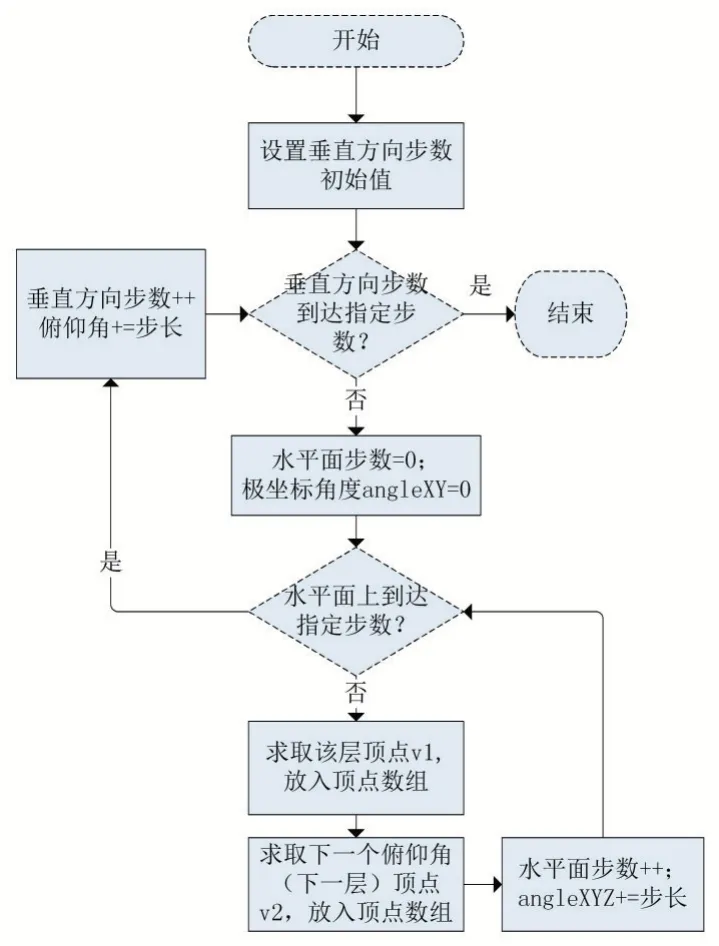
图2 生成顶点流程

自由空间下，实际上每一层的包络相当于一个给定半径的圆，这种情况下使用极坐标来表示后可以很容易生成在世界空间下的坐标，当在地球上显示时则要转换为地球经纬度表示。

1.2 雷达探测概率

（1）雷达探测概率理论

雷达信号的检测并不能达到完全准确，可能会由于接收电路中的噪声电压产生一定的误差。将信号出现时被探测到的几率定义为Pd，将Pfa定义为接收系统产生的噪声波动被误认为是信号的概率，也即虚警概率。

对于雷达探测概率的计算有多种计算模型可以使用。主要有两种，一是针对稳定目标的Marcum 模型，一是针对起伏目标的Swerling 计算模型。

Marcum 模型[7]：

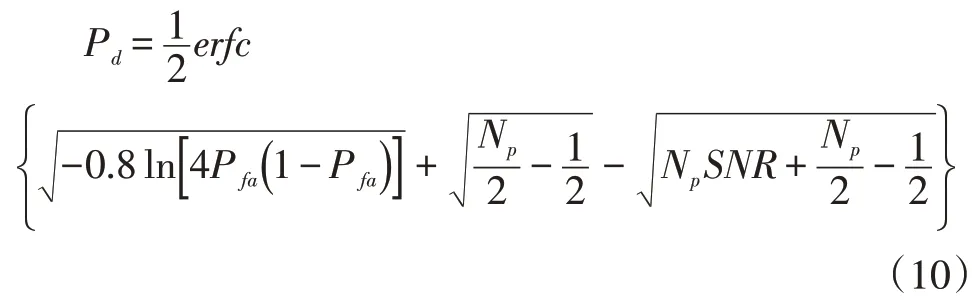
我们可以根据其函数图像得知：

图3 余误差函数曲线图

当x 小于-2 时的值是确定的，概率会恒等于1。也即对于Marcum 概率公式，只有当 x，满足一定的条件时，求出的概率值才是有效的，由于虚警概率这里相当于常数，因此当累计脉冲数Np 达到一定值时，才能求出较为正确的概率值。

（2）雷达探测概率可视化

自由空间下，在忽略地形遮挡的情况下（若遮挡时，探测概率为0），同样将空间分层，但是在每一个水平方向上，我们只需要根据一个轴（例如X 轴）的方向来设定步距求每一点的概率值。每一点的概率都不相同，我们这里构造概率为0.5、0.7、0.9 的包络面。

求出满足条件的坐标后我们获得它距雷达的距离以及俯仰角，构造出该水平层上所有的坐标，再求出垂直面上所有层的坐标，每一层的坐标数量相等，可以采用四边形面元，逆时针分别将原数组中的点以及右边，右上，正上方的点加入最终的顶点数组中用于构造包络。

求满足条件的坐标流程如图4。

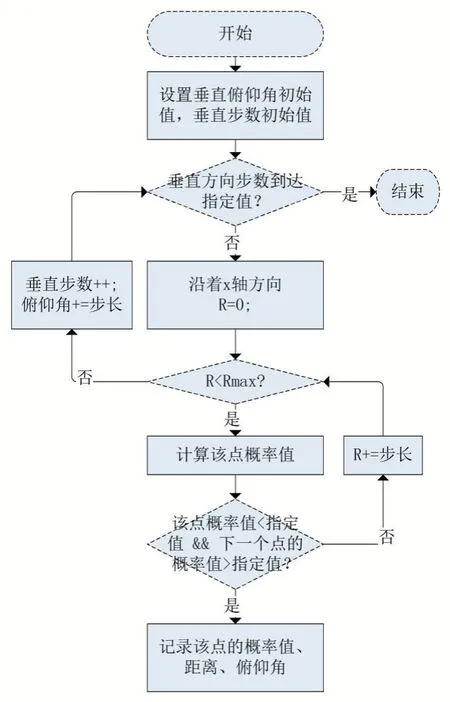
图4

计算概率的过程中根据Marcum 公式我们需要先进行信噪比的计算，然后进行概率值的计算。由于最小信噪比是我们给出的，且根据最大距离公式反推我们可以得到：

可以推出：

构造最终顶点坐标的流程如图5。

1.3 影响雷达探测范围的因素

（1）干扰机干扰

作战时或遇到其他情况时，雷达不仅会接收到它本身发出的电磁波，还可能收到自然界产生的或干扰机发出的干扰信号。当有多个干扰机存在时，目标雷达接受信号功率需要进行修改，干扰信号功率进行累加就可以得到目标雷达能够接收到的总干扰信号的值：

此时关于雷达信噪比的计算要将分母加上接收到的干扰机的信号功率，调整为：

（2）地形因素

崎岖的地形、山坡山峰等会阻碍电磁波的传播。因此我们需要通过雷达位置到边界点的连线是否受到地形阻挡来重新定义边界点。

其思路是：与自由空间下雷达最大探测范围模型求取顶点的步骤相同，但是要根据地形对顶点位置进行调整。从雷达所在的坐标处向该方向发射一条射线，射线的长度以100 米为单位递增，计算该射线到达处的坐标值以及高程值，如果该处的地形高度值大于该处顶点的高度，说明遇到阻挡，将该点记录下来，如果没有遇到阻挡且不超过边界范围，将边界点记录。

根据地形因素重新规划顶点的流程如图6。

图5

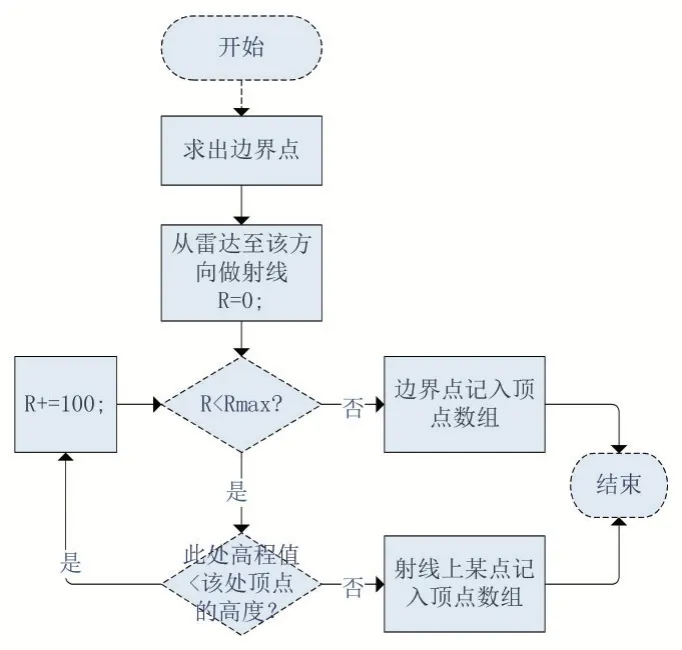
图6

（3）大气因素

晴朗天气下，空气不含恶劣天气下的各种粒子，而主要应该考虑的是氧气和水蒸气的作用。它们会对吸收电磁波，造成电磁波的衰减。

如图7 所示。

根据资料，有多种模型可以用来描述大气的吸收作用，与之有关的因子为高度和频率：

Libebe 模型计算吸收衰减率为[5]：

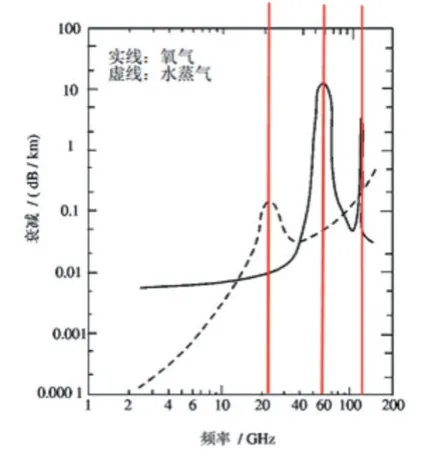
图7 大气衰减曲线图[5]

ITU-R 模型将大气吸收率表示为氧气和水蒸汽的吸收率的和[5]：

恶劣天气下也会对电磁波的传播产生影响，如在不同的降雨强度下，不同频率的电磁波的衰减程度如图8 所示。

图8 电磁波在不同降雨强度下的衰减[6]

2 结语

目前实现了在自由空间中对高斯型、SINX∕X 型的单基地雷达的最大探测范围的可视化。定性讨论了影响雷达探测范围的因素——地形遮挡、大气折射、大气吸收，进行了单部雷达的探测概率的理论研究和建模。

在任意点处建造出的雷达最大探测范围模型如图：

高斯型雷达：

图9 高斯型雷达参数说明

图10 高斯型雷达最大范围建模

SIN（X）∕X 型雷达：

图11 SIN（X）∕X型雷达参数说明

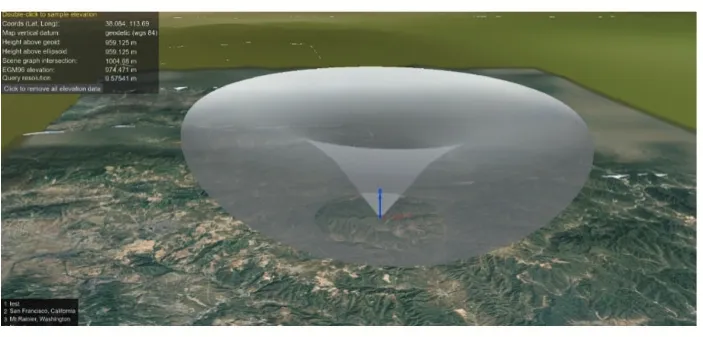
图12 SIN（X）∕X型雷达建模

地形影响下的建模如图13 所示。

图13 地形影响下的高斯型雷达建模

雷达的探测概率模型如图14 所示。

图14 雷达探测概率可视化模型

其中红色表示概率为90%，黄色表示概率为70%，蓝绿色表示概率为50%。