改进K-means 聚类剪枝的DTW 动态手势识别方法

倪庆千，乔冀瑜，连宗凯

（中山大学智能工程学院，广州 510006）

0 引言

手势是一种简单而自然的交流方式，也是人机交互的重要手段。手势识别可理解为通过计算机理解人的手部语言。由于人体的灵活性使得动态手势丰富多变，建立计算机识别模型困难[1]。现有模型非特定人适应性弱、手势库容量小[2]，因此需要探究更加适宜处理大量动态手势动作的方法。

从识别设备的角度，目前手势识别主要可分为基于计算机视觉的手势识别和基于可穿戴设备的手势识别[3]。基于视觉的手势识别利用图像视频处理技术和深度学习[4]等技术，例如基于Kinect 的手语翻译系统[5]、基于Leapmotion 的手势识别系统[6]及王凯等人提出的基于AdaBoost 算法和光流匹配的实时手势识别方案[7]。基于视觉的方案优点有识别精度高、容量大和动作自由等，但是易受光线、背景等环境因素影响，同时由于需先做大量预处理，计算消耗成本高[1]。基于可穿戴设备的手势识别利用多种传感器，例如早在1983 年AT&T的Grimes 原创性发明了数据手套[8]、2016 年Facebook的VR 交互设备Oculus Touch、郑锦龙团队的穿戴式手语识别翻译系统[9]等，可穿戴设备虽然无法无感识别，但具有高精度高灵敏度、数据结构简单以及计算成本低的优势。

从识别方法的角度，主要有基于模板匹配的方法、基于统计模型的方法和基于人工神经网络方法[2]。模板匹配是一种在模板库中寻找特定目标的常用策略，这种方法遍历比较所有可能的对象获得相似度，并从中选出相似度足够高的结果，认为其与模板匹配。常见方法有动态时间规整（Dynamic Time Warping，DTW）[10]。统计模型则以概率为基础，采用数学统计的方法建立难以通过理论分析建立数学，但可以通过大量数据统计变量之间函数关系的模型，常见方法有隐马尔可夫模型（Hidden Markov Model，HMM）。人工神经网络的方法则通过调整网络内部大量节点之间相互连接之间的关系从而处理信息，经典模型有BP 神经网络（Back Propagation Neural Network）、卷积神经网络（Convolutional Neural Networks，CNN）[11]、循环神经网络（Recurrent Neural Network，RNN）[12]。统计模型、人工神经网络模型方法适合解决高复杂度问题，但需要大量清洗过的数据，且计算量大，扩展弹性差。模板匹配方法所需数据量少，可动态扩展模板库以识别新的手势，但在待识别手势模板较多时，遍历比较会导致识别速度慢、识别正确率降低的问题。

根据上述分析，研究从设备成本、数据量和可扩展性的角度考量，着力研究缓解动态手势识别宽容度、识别容量、识别速度和识别精度之间的矛盾。我们基于可穿戴数据手套，提出一种改进K-means 聚类剪枝的DTW 动态手势识别方法。该方法首先以DTW 为度量，对手势模板库的片段序列进行K-means 聚类预处理。在此基础上，先对当前传入手势序列的片段使用DTW 确定所在类，然后在类内采用整个序列进行DTW模板匹配，获得最终识别结果。经过实验验证，我们提出的手势识别方法具有成本低、计算速度快、可扩展性优良等优点，具有成为手势交互底层技术的潜力。

1 数据手套手势采集系统

1.1 硬件系统简介

数据手套手势采集系统的硬件部分为左右手两只手套（GloveR，GloveL），每只手套由姿态传感器模块Mpu9255、弯曲度传感器 Flex2.2、2.4G 通信模块NRF24l01、蓝 牙 通 信 模 块 JDY- 08、主 控 模 块STM32F103RCT6 及周边电路构成，电路结构示意图与实物图如图1、图2 所示。

图1 电路结构示意图

图2 数据手套实物图

其中Mpu9255 为九轴传感器，手部姿态的变化会引起内部传感器的参数变化，用于获取手部姿态信息；Flex2.2 为长条状电阻应变片，通过与标准电阻进较的电压差，获得手指弯曲程度；NRF24l01 负责左右手套内部数据通讯，JDY-08 则负责数据手套最终数据对外通信；STM32F103RCT6 为控制核心，负责传感器数据采集、数据规整与无线通讯调度。

1.2 数据格式

数据手套通过蓝牙对外发送原始数据，其每次发送十个手指的弯曲数据与手部的运动姿态数据，令为O=[Rcurvature,RAcc,RGyro,Lcurvature,LAcc,LGyro]，动态手势数据按时间顺序取得序列S={O1,O2,…,On}。

2 改进K-means聚类预处理

动态时间规整DTW 本质上是一种模板匹配方法。当手势模板过多时，如果直接使用DTW 和模板手势库逐个遍历比较，则计算量与手势模板量成线性增长，最终获取结果只有一个，存在大量无效计算。因此，文章采用K-means 聚类算法对原始序列进行聚类预处理，形成剪枝减去无效计算。

K-means 是一种常见的动态迭代求解的无监督学习算法[13]。K-means 聚类算法计算速度快，算法思路清晰，并且聚类效果较好。在原始K-means 算法的基础上，我们提出以DTW 相似度为度量指标，替代传统的欧氏距离用于评价序列之间的距离，以解决使用欧氏距离难以准确计算时序序列之间距离的缺陷。

以DTW 相似度为距离度量的K-means 聚类主要分为两步：一是动态时间规整算法计算不同手势片段序列之间的相似度；二是基于DTW 相似度，给定K 值与随机初始中心进行K-means 聚类迭代，获得K 个类簇及相应聚类中心。

2.1 动态时间规整算法计算相似度

由于人体的灵活多变性与个体差异，同一个手势不同的人做出来时，动作速度、运动轨迹和运动节奏存在差别，甚至同一个动作由同一个人在不同时间做出相同含义的手势也存在差别。这使得数据手套传入的时序序列数据在时间轴上存在不完全对齐现象，同时又无法通过线性缩放的方法对齐。DTW 通过对时间序列进行局部非线性缩放，使两个序列形态尽可能对齐，如图3 DTW 示意图所示。

动态时间规整算法原理是给定两个序列Q={Q1,Q2,…,Qi,…,Qn} 和C={C1,C2,…,Cj,…,Cm} ，其长度分别是n和m。构造一个n*m的矩阵网格，以欧氏距离D为标准，矩阵元素(i,j)为Qi和Cj两个点的距离D(Qi,Cj)。从序列起始段所在的矩阵角为边界条件，满足连续性和单调性约束，通过动态规划求得距离累积值最小的路径即为最佳路径。

图3 DTW示意图

此时，最佳路径的累积距离值即为两个序列的DTW 相似度，即两个时间序列经过非线性缩放后的最小距离。

2.2 基于DDTTWW相似度进行K-mmeeaannss聚类

基于DTW 相似度的K-means 算法原理是给定聚类数k，随机选择k 个对象最为初始聚类中心。接着以DTW 相似度为距离度量，计算每个样本序列和各个中心之间的距离，将序列划分给距离它最近的中心，形成k 个聚类C={ }C1,C2,…,Ck。再重新计算每个聚类的均值作为新的中心。反复执行上述步骤直至各聚类中心移动幅度小于设定阈值ε。K-means 算法是动态迭代直至收敛的过程，流程如图4。

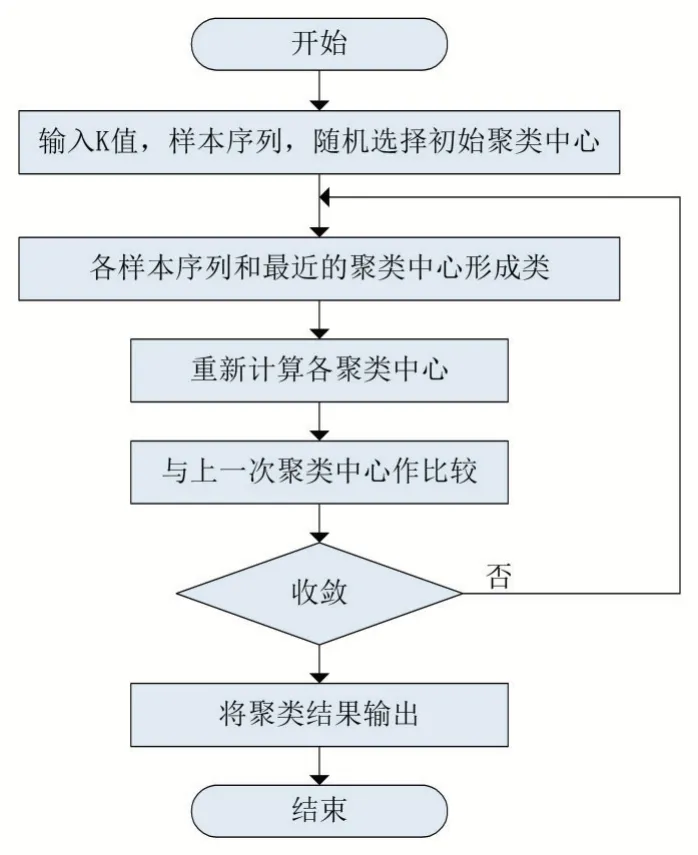
图4 K-means算法流程图

由上分析可知，K-means 算法需要根据序列之间的距离来判断序列之间的远近。但是传统的欧氏距离难以合理计算时间序列之间的距离，因此使用序列之间的DTW 相似度来代替欧氏距离是有必要的。

3 DTW动态手势识别算法

在对模板手势库进行K-means 聚类预处理后，将所有手势分有k个类，每个类别取出聚类中心作为类等代表序列ri，令所有类均取出的组成集合R={r1,r2,…,rk} 。

开始识别手势动作时，对于数据手套新采集的完整序列，取相应片段依次与R 中片段序列通过DTW 进行比较，DTW 计算结果最小值所对应的类C，确定为新序列所归属类别Ci。再将完整序列依次与类Ci内完整序列进行比较，直到得到DTW 计算结果最小，即相似度最高的序列，即为最终动态手势识别结果。具体流程如图5 所示。

图5 手势识别流程图

4 测试结果与分析

针对动态手势识别，实验从识别容量、平均分类正确率、平均识别正确率、平均识别运算时间标准差、聚类后∕前识别所需时间比和扩展比率几个性能指标，用以评估所提出方法的有效性。

其中，识别容量分别设置为Vi={8,16,32,64,128}，平均正确率计算公式为：

当式1 中x为Class时为平均分类正确率，x为Gesture时为平均识别正确率。

平均识别运算时间公式为：

上述三项目平均值的有效性，我们利用标准差Si来计算其原始数据的离散程度，标准差Si可由下式表示：

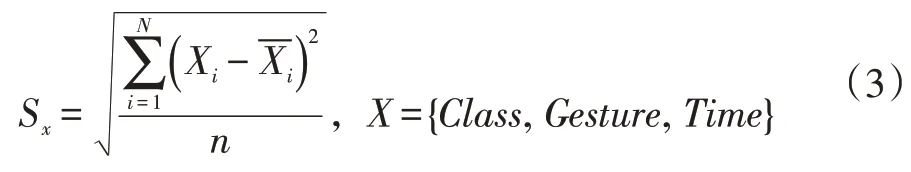
为了说明该算法的可扩展性，我们提出聚类后∕前识别所需时间比例Time scale和扩展比率Expansion ratio来量化衡量，其中Time scale为聚类后平均识别时间除以聚类前平均识别时间，从识别时间的角度评估识别效率的改进程度：

同时，从时间角度也可从平均识别时间提升倍数Time multiplier的角度说明效率的改进程度，其值为Time scale的倒数，即：

扩展比率Expansion ratio用于刻画所提出该方法的在可用范围内的容量扩展能力，表示为识别手势量的提升比例、提升后平均识别正确率与平均识别时间提升倍数三项乘积，即：

式（2）、（6）中NumGes为手势数量，式（6）中T为第几次实验为平均识别正确率。

4.1 模板手势库

模板手势库数据是由根据《中国手语（上下修订版）》中示意手势，由实验员采集和维护。手势库数据包括了数字“1-9”、字符“A-Z”、肯定否定、动作词和问候等常用词汇。

表1 模板手势库

4.2 实验流程

首先，对已有模板手势数据库进行改进K-means聚类预处理，输入不同的k 值和随机选取的初始序列中心，迭代获取不同k 值下的聚类结果C。其次，实验员戴上数据手套，手套，将感知到的双手数据通过蓝牙传输至上位机。上位机通过串口读取数据，获得实时输入的当前手势序列。

最后，将实时输入的当前手势序列，取出对应片段与K-means 聚类预处理后的类代表序列片段R进行DTW 运算，确定当前手势所在类C。再将完整当前手势序列依次和类内完整序列进行比较，直到得到相似度最高的序列，获得其对应手势含义，即为最终动态手势识别结果。

上述过程可由图6 简要概述。

4.3 实验结果及分析

按照上述实验说明，实验结果如表2 所示。

图6 手势识别流示意图

图7 实验结果

表2 实验结果

在扩展性上，首先在图7（a）中可以看出随着识别容量的扩展，时间消耗大幅度缩小的趋势更加明显。其次从表2 扩展比率和图7（b）可以看出，扩展能力随着识别容量的成倍增大而先上升后下降的。在识别容量翻16 倍时，所需分类迭代次数和识别时间仅仅增长不到4 倍，并仍在可控范围之内。如图7（c）所示，高扩展低消耗来源于聚类剪枝，我们采用完整时序数据片段做聚类处理，针对时序序列的特点使用DTW 作为聚类内容相似度的度量指标。

5 结语

我们提出改进K-means 聚类剪枝的DTW 动态手势识别方法，旨在实现非特定人大量动态手势的高效识别。本文从构建获取与处理数据的数据手套入手，基于动态手势时间序列的特性，提出采用DTW 作为距离度量的无监督的改进K-means 聚类方法，有效消解了时序数据不完全对齐的问题，具备良好的伸缩性和高效性。明显且可控地提高了动态手势的识别速度和精确度，达到良好效果，有较高的实际应用价值。

无论是手势识别或手语翻译技术均是大有裨益的研究，该研究提供肢体动作这一个在计算机视觉、听觉与脑机接口外更符合直觉的维度，这些多模态信息有助于让机器理解人类更近一步，充分的实验和实验结果验证了我们的想法。

我们也应当注意到这项工作的局限性：数据手套虽然使用方便，在日常使用中却会稍显笨重无法无感使用；模板手势库若用语手语翻译，则数据库大小仍然过小；采用的算法虽然经典，但其适用范围存在局限性，同时存在无法确定实际数据分布情况与需要手动赋值k 值和阈值ε参数的问题；原始数据分布无法明确其在高维空间是否为簇状分布，采用的K-means 算法对非簇状；算法是串行计算的，并行程度相对最新的深度学习算法略逊一筹的同时却无法计算长序列。这些未解决的问题有待进一步探讨和研究，这说明了这个领域还有广阔的进步空间，我们期待在未来的工作中能进一步解决这些问题。在下一步工作中，我们将改进数据采集设备，继续扩展模板手势库，尝试将深度学习算法和动态手势识别相结合，以进一步调高识别的准确率与识别速度，并尝试解决连词成句的长序列的问题，使其能有效应用于手语翻译或复杂的交互手势识别。