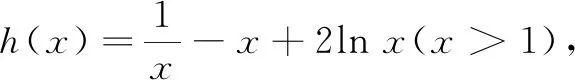两类均值不等式的简单应用*
周思宇
(湖南省长沙市周南中学,410005)
极值点偏移问题是近几年高考的热点问题,求解此类问题的一个重要工具就是指数和对数均值不等式.本文借助几类典型例题加以说明,希望能对读者的高考复习提供帮助.
一、两个均值不等式
1.对数均值不等式
结论1对任意的a,b>0(a≠b),有
证明不妨设a>b(a 2xlnx-x2+1<0. 2.指数均值不等式 结论2对任意实数m,n(m≠n),有 证明在对数均值不等式中,令em=a、en=b,则m=lna,n=lnb,从而可得指数均值不等式. 评注需要注意的是,在实际解题过程中,凡涉及这两类不等式的,都需给出证明,以确保考试不被扣分.本文在应用举例中都省略了该过程. 例1已知函数f(x)=alnx(a>0),若A(x1,y1),B(x2,y2)(0 再令h(t)=tlnt-t+1(t>1),则h′(t)=lnt>0,h(t)在(1,+∞)单调增,h(t)>h(1)=0,故t-1 综上,得证. 2.“f(x1)±f(x2)”型问题 (1)讨论f(x)的单调性; (2)若f(x)存在两个极值点x1,x2,证明: (2)若f(x)存在两个极值点,由(1)知a>2. 3.极值点偏移问题 例4若函数f(x)=lnx-ax(a为常数)有两个不同的零点x1,x2,请证明:x1x2>e2. 证明借助a作为媒介,构造对数均值不等式.



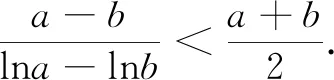
二、应用举例