指向儿童数学素养提升的学习评价材料设计

朱俊华

摘要：学习评价是课堂教学的重要环节之一，是评价课堂教学效率、反馈学生学习效果、调控教师教学路径的重要手段。“有营养”的学习评价材料就应在学生学习中发挥关键性作用，指向学生数学学习的关键能力的提升，如阅读理解的能力、灵活思辨的能力、归纳推理的能力和综合运用能力等等。

关键词：学评材料;情感式;开放性;关联性;融合性

学习评价是课堂教学的重要环节之一，是评价课堂教学效率，反馈学生学习效果，调控教师教学路径的重要手段。有人把学习评价简单等同于做练习题，其实不然。不可否认，练习题是学习评价的重要载体，但学习评价关注的是知识形成的过程，是学生把知识转化为能力的重要途径，也是学生形成学科素养的重要载体。数学学科素养的培养须要有一个不断渗透、由浅入深循序渐进的过程。而这一过程，需要教师不断用“有营养”的学评材料启迪学生的思维，让他们在一次次的探索过程中，不断地反思与积累、感悟与提升。何为有营养的学习评价材料？就是能在学生学习中发挥关键性作用，形成关键能力（如阅读理解的能力、灵活思辨的能力归纳推理的能力和综合运用能力等）的材料。

一、设计情境式学评材料，培养学生阅读理解的能力

《义务教育数学课程标准（2011版）》（以下简称课：程标准）强调，课程内容要反映社会的需要、数学的特点，要符合学生的认知规律。课程内容的选择要贴近学生的实际，有利于学生体验和理解、思考和探索叫。在设计学评材料时，既要关注学生的认知基础，连续他们的已有经验，还要创设适合他们探究的富有情趣的问题情境，让他们具有熟悉感和亲切感。同时在创设情境时，要尽量做到真实，最好是生活中的情境再现。学生在解决此类问题过程中，逐渐培养阅读分析、理解、整理等能力，进而培养发现和解决实际问题的能力。

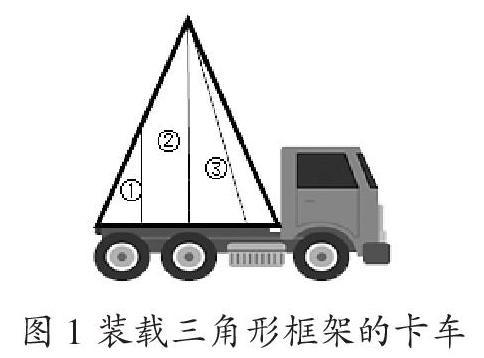
比如，在教学苏教版《数学》四年级下册认识三角形平行四边形和梯形时，都要研究它们的高。实践证明学生对高的理解一直是难点，主要有两个原因：一是定义的抽象性。书本上给出的三角形高的定义是：从三角形的一个顶点到对边的垂直线段，叫做三角形的高。看似簡单的一句话却包含着大量信息，也很抽象，尤其是学生对“垂直线段”的理解普遍存在困难。二是受生活中高的负迁移。平面图形的高和生活中的高既有联系又有区别。一般情况下，生活中的高特指垂直于底面，而图形中的高却不是。

学生第一次接触高的概念是在认识三角形时。虽然平行四边形和梯形的高与三角形的高有区别，但本质上是一致的，所以三角形高的认识显得十分重要。教学时，笔者设计了这样的问题情境：一辆卡车装载着一个三角形铝合金框架，竖直绑在卡车上，路，上遇到一个限高4米的隧道，已知卡车车厢距离地面1米，三角形铝合金框架内有三条线段，司机须要测量哪条线段的高度才能决定是否可以通过这个隧道？（图1）对比这三条线段，①号和②号线段都是垂直于底边的，②号和③号线段都是从三角形顶点到对边的线段。学生联系生活经验认识到：能代表这个三角形高度的必须是既要从顶点到对边，又要垂直于底边的线段（②号线段）。通过讨论，学生还发现从三角形一个顶点到对边的线段中，只有垂直线段是最短的，并且是唯一的一条。这条“特殊”的线段就是三角形的高。教师继续追问，如果三角形的框架变换一个方向，那它还有其他的高吗？学生研究发现三角形有三条高，从顶点到对边的垂直线段都是它的高。

学生在分析哪一条线段能够代表这个三角形框架的高度的过程中，逐步感受到三角形的高的两个重要特征：一是从顶点到对边的线段，二是必须垂直于对边。这样的教学充分遵循学生的认知经验，从学生熟悉的生活场景出发创设问题情境，在解决问题的过程中建构概念，实现了基于生活又高于生活的数学化过程。学生对三角形高的理解不再停留在抽象的数学：术语，而是更加直观形象地感受高的特征。这样的学材设计既重视高的本质概念的揭示，又激活了学生的生活经验，启发他们深度思考。

二、设计开放性学评材料，培养学生灵活思辨的能力

开放性学评材料往往不像封闭性材料那般“直截了当”，较少透露可以直接解决问题的数学知识或者步骤，需要学生综合分析题千中的相关概念的数学意义、自主规划解决问题的过程、构思可能的答案形式、选择合适的表述来表达自己的观点。所以，开放性问题需要学生面对相关数学问题时，根据自己的理解做出个性化判断，提出自己的观点，并把自己的注意力转向所描述的比较具体的某个方面。开放性学评材料需要学生综合运用数学抽象和数学推理进行深度思考和创新思维，给出自己的理解和结论。所以，开放性学评材料有利于培养学生发散思维和创新能力。

比如教学苏教版《数学》四年级下册“一亿有多大”。笔者设计了这样的问题：一般情况下，100粒米的重量大约是2克，如果每位小学生每天浪费一粒米，那么全国约1亿小学生，一天大约浪费粮食多少吨？目前全球有40个国家面临不同程度的粮食短缺，约10亿人口营养不良，每年更是有560万儿童因饥饿和营养不良而死亡，在发展中国家约有五分之一的人口无法获得足够的粮食。读了这段话，结合上面的计算，你想说什么？

一亿对学生来说是一个无法感受的巨大数字，如何帮助学生建立一亿有多大的表象、如何培养学生的“量感”成为这节课的重点。学生在解决这个问题时，答案是开放的：学生发现一亿粒粮食竟然有那么多，有的说要从自身做起节约粮食，有的说要做一个爱惜粮食拒绝浪费的推广大使，有的说要靠科技的力量加大粮食产量，满足全球人口的需求，还有人说发达国家要有担当精神，支援发展中国家，中国要尽快成为发达国家等等。

孩子们的思维没有局限于一个维度，而是开放的、创新的。同时，这样的学评材料也培养了学生用数学眼光看问题，用数学头脑思考问题的习惯，体现了数学学科的育人价值。

三、设计关联性学评材料，培养学生归纳推理的能力

数学知识本身具有严密的逻辑结构，知识之间存在着元素关联，同单元、同领域、同学科、学科间也都存在着结构关联。学评材料就是要帮助学生弄清楚知识元素之间的联系，理清知识的来龙去脉，看清知识的生长序列，使学生有意义地进人数学学习，整体动态地开展学习层阶活动。

比如教学苏教版《数学》五年级下册“一个数是另个数的几分之几”时。这节课是学生学习了分数的意义以及分数与除法之间的关系后学习的内容。之前学生认识的分数都是表达部分与整体的关系，显然这样的认识是不全面的，分数除了表示部分与整体的关系外，还可以表示两种不同量之间的倍比关系。这又分数认识的一次跨越，并且这节课中还能够把分数意义、分数与除法的关系、假分数、分数与“倍”的关系等知识关联起来，实现从“知识点”到“知识链”，再到“知识块”的结构化提升。

教学时，笔者充分利用变式组织教学，让相关的知识形成结构。课始，出示一条红色彩带，平均分成四份，问每份是这根彩带的几分之几？以此来复习分数表示部分与整体之间的关系。接着把一份的红彩带从原图上移下来变成黄色，问现在黄彩带的长度是原来红彩带的几分之几？学生通过推理发现黄彩带与原来红彩带的一样长，所以黄彩带的长度是红彩带的，或者根据分数的意义，把红彩带看成单位“1”，平均分成四份，黄彩带的长度表示这样的一份，所以黄彩带是红彩带的一。教师追问，反过来红彩带的长度是黄彩带的几倍？通过对比，学生发现以前学习的“求一个数是另一个数的几倍”和今天学习的“求一个数是另一个数的几分之几”有着密切的联系，都可以用除法计算。接着再变：在原图上又出现了一根蓝彩带，表示红彩带的三份，问学生你又能用分数表示什么关系？学生讨论后得出，蓝彩带的长度是红彩带的产，反过来红彩带的长度是蓝彩带的4，黄彩带的长度是蓝彩带的六，蓝彩带的长度是黄彩带的3倍*...最后，紅彩带的长度变成m（m#0）米，蓝彩带的长度是n（n#0）米，问红彩带的长度和蓝彩带又可以用什么分数表示？

通过一题多变的“题组”方式呈现，使学生感受到在解决同一类问题时知识之间的不同维度的关联性。这样的教学既有利于学生整体思维的形成，也能有效防止思维僵化现象的发生。

四、设计融合性学评材料，培养学生综合运用能力数学课程标准把课程内容分为数与代数、图形与几何、统计与概率综合与实践四大领域，但是实际生活中可能不只是涉及某一个领域，既有领域之间的融合，也有跨学科的融通。学生在解决实际问题时，须要灵活运用各个领域的相关知识和方法。所以，教学时应该有意识设计融合性学评材料，帮助学生提升综合解决问题的能力。

比如教学苏教版《数学》五年级下册“圆的认识”，笔者设计了如下问题：请同学们在方格图上画出一个圆，要求图上的点A和点B都在圆上，请用数对表示出这个圆的圆心0，对比这三个数对，看看有什么发现，从中我们还能想到什么（图2-1）？这个问题需要学生综合运用圆的特征结合数对的知识解决，并且这个问题的答案并不唯一。刚开始，学生只能找到一个圆心（图2-2），并且能用数对（5，5）表示出来。然后，学生又发现符合条件的圆不止一个，当圆心的位置在（5，4）时也符合要求（图2-3）。继续研究，发现这些圆虽然位置不同，但是圆心都在一条直线上，并且有无数个（图2-4）。在研究过程中，学生对“圆心确定圆的位置”的数学特征感受强烈。

好的学评材料既要兼顾学生的个体差异，能满足不同学生的发展需求和思维进阶，又要促进知识的关联融通，提升学生综合运用能力。圆的认识学评材料的设计，既有本节课不同知识点的巩固，又融合了不同领域的知识（图形与几何和数与代数），还融通了数学思想方法，如数形结合思想、极限思想归纳推理思想和整体思想等等。

学习评价是学生学习和教师教学不可或缺的关键环节，聚焦于学生学科核心素养的新追求，最终指向完整人的发展。学生的学习能力和综合素养须要有科学的学评材料作支撑，好的材料能够彰显学生的主体地位，能够打开学生的思维，让学习真正发生。

参考文献

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[2]吴维维，邵光华逻辑推理核心素养在小学数学课堂如何落实[J].课程.教材·教法，2019（03）.

[3]徐宏臻，陆兆芬.“图形的认识”教学要注重发展数学思考[J].小学数学教育，2019（01/02）.

[4]万兆荣.依学而生：小学数学结构化学材开发[J].教学与管理，2018（11）.

[5]顾正理.PISA测试对小学数学教学评价的启[J].小学数学教育，2019（01/02）.

[责任编辑：陈国庆]