山东省区域创新能力时空双维实证评价研究——基于PFHWD-TOPSIS模型

王家明，张云菲，丁 浩

（1.中国石油大学胜利学院 文法与经济管理学院，山东 东营 257061；2.中国石油大学（华东）经济管理学院，山东 青岛 266580）

一、引 言

创新作为高质量发展的核心动力，是塑造国际竞争优势的关键。在后金融危机时代，创新对于突破经济发展瓶颈，解决深层次矛盾和问题有着巨大的促进作用。随着我国经济发展进入新常态，我国的经济发展由高速增长转为高质量发展，创新驱动的潜力再次被激发。“十三五”提出要牢固树立并切实贯彻“创新、协调、绿色、开放、共享”的五大发展理念，且强调创新理念为五大发展理念之首；十九大报告明确提出加强国家创新体系建设，坚持创新驱动发展战略，建设创新型国家，可以看出：我国始终坚持以创新引领全国经济、科技、社会的高质量发展。整体看来，我国创新驱动取得了一定的提升，但与发达创新型国家相比仍存在一定差距，尤其在制度创新方面，据《2018 年全球创新指数报告》显示，“创新产出”排名第10 位，“创新投入”排名第27 位，“创新效率”排名第3 位，但“制度环境”分项排名为第70 位。事实上，我国已充分认识到制度创新能力不足的问题，且提出科技创新、制度创新要协同发挥作用，共同促进系统创新水平的提升。而这里的制度创新更多的是如何从创新要素角度系统的创新。《2019 中国区域创新能力排名》显示山东省居全国第6 位，与同期相比位次不变，但创新指数略有下降。在此背景下，本文结合山东省区域创新实际，以DPSIR模型为思路构建山东省区域创新能力的初步评价指标体系，并引入指标回路法进行优化完善，组合赋权后形成最终的山东省区域创新能力评价指标体系。在此基础上，借鉴前人研究［1］，改进传统经典的 TOPSIS 模型为 PFHWD-TOPSIS 模型，对山东省17 地市（鉴于时间维度考虑，并未将莱芜市并入济南市进行合并计算）2009-2018年区域创新能力进行时空双维实证评价研究，旨在为同领域专家的研究做出补充与借鉴，为山东省17地市区域创新政策的制定提供参考，促进其科技创新与制度创新共同提高的区域高质量发展，具有一定的理论应用创新与实践指导意义。

二、文献综述

本文运用PFHWD-TOPSIS对山东省17地市区域创新能力进行时空双维实证评价分析，主要涉及区域创新能力、PFHWD-TOPSIS 两大主体，故文献综述也以此为线索展开。

（一）区域创新能力的相关研究

纵览现有国内外专家学者对区域创新能力的相关研究，可以得出：现有文献大都从区域创新的来源、定义、意义、影响因素、评价等方面进行研究，同时有专家学者引申至区域创新系统并进行相关研究。

1.区域创新的内涵及外延相关研究

从区域创新理论的产生来看，大概可分为创新概念、创新理论和创新驱动三个角度。创新概念的提出始于约瑟夫·熊彼特，其最早提出创新，并赋予其经济意义；从创新理论角度来看，学术界统一认为起源于马克思的政治经济学，特别是其科技创新思想；从创新驱动的角度来看，则起源于迈克尔·波特的《国家竞争优势》中提到的经济发展的四个阶段。国内多位专家学者认为创新是对传统的打破，表现为技术的“新奇性”［2-3］和“市场价值的实现性”［4］，强调技术创新的市场属性。张利珍等［5］认为，相对于单一的技术要素而言，创新驱动以科技创新为核心，是国家发展的阶段性特征；同时他提出创新文化是前提，人才是根本，制度创新是保障。

2.区域创新能力影响因素相关研究

区域创新能力的提升是系统化的科学问题，很多专家学者分别从各自角度对其进行研究。石峰等［6］就劳动投入对区域技术创新的影响进行研究；另外，还有很多专家学者研究得出，技术创新网络组织、制度环境、管理团队认知风格对区域创新能力有着不同程度的影响。

除此之外，多位学者运用线性回归方法研究了区域创新能力的影响因素，如区域创新维度［7］、虚拟整合网络能力［8］、企业技术创新［9］等；运用基于VAR 模型的时间序列回归分析研究了区域创新的影响因素，如对外开放［10］、出口［11］、专利申请和知识产权保护［12］、风险投资［13］；运用一般面板数据回归分析区域创新的影响因素，如知识连接和关系强度［14］、区域科创网络［15］、不同政府支持路径［16］；运用面板门槛回归模型的相关研究，如产业集聚［17］、研发投入［18］、研发要素流动［19］、人力资本［20］、FDI［21］、OFDI 逆向技术溢出［22］、政府支持［23］；运用面板分位数回归模型的相关研究，如技术市场发展水平［24］、环境规制［25］、科技创业企业创新行为［26］、高等教育空间集聚［27］；运用离散数据回归分析模型的相关研究，如创新网络交互度［28］、区域“产—学”知识生产网络［29］、多维邻近性［30］。

3.区域创新能力评价相关研究

鉴于区域创新的效益与贡献，多位专家学者从理论与实践角度对区域创新能力的评价模型与实证评价展开研究。现有对区域创新能力评价模型的相关研究较多：模糊综合评价法，如张卫国等［31］；聚类综合评价法，如周立等［32］；灰色综合评价法：姜文仙［33］；DEA 模型，如刘顺忠等［34］、余泳泽等［35］；TOPSIS 模型，如董秋霞等［36］、霍明等［37］；RBF 神经网络分析法，如冯岑明等［38］。同时，不少专家学者对不同区域的创新能力进行实证评价研究，如Edgington D W［39］等。

4.区域创新系统相关研究

国内外专家学者对区域创新系统的研究是由对区域创新能力的相关研究引申而来的，现有研究大都从区域创新系统的定义、内涵与外延、组织类型、空间结构等方面展开。区域创新系统的概念最早是由Philip Nicholas Cooke提出，Autio E［40］进行补充，认为区域创新系统是基本的社会系统，内部子系统的互动推动区域创新。Cooke P等［41］将区域创新系统分为基层创新系统、网络型创新系统、统制型创新系统，随后很多专家学者在其基础上进行区域创新框架的研究，并从公共政策、创新中介、教育系统、风险资本市场等进行深入。同时，有部分专家学者对区域创新系统的创新政策及企业行为进行研究。张俊芳等［42］认为，应将创新政策分为鼓励创新行为、激励创新主体和营造创新环境；潘文庆［43］在比较和借鉴发达国家双创支撑体系的基础上，对我国创新政策体系的具体内容提出了完善建议；程石磊等［44］主要以Logit 统计模型和Bayesian 决策理论为基础，将其整合为一个逻辑整体，研究企业创新决策的偏向。

（二）PFHWD-TOPSIS的相关研究

TOPSIS 是经典的多属性评价模型，由Hwang C L 等［45］提出，又名优劣距离解法，其基于拟定的指标与理想化的结果之间的欧氏距离，对评价客体进行相对优劣的评价，是一种逼近理想解的排序方法。因其灵活性高，计算简便，被不断改进并广泛应用在多属性决策、经济社会评价等多方面，如绩效评价［46］、竞争力评价［47］、环境评价［48］等；与此同时，TOPSIS方法在应用过程中不断结合改进，衍生出一系列的组合方法，如熵权TOPSIS［47-48］、PCA-TOPSIS［49］等。

1965 年，自动化领域的专家 Zadeh L A［50］提出了模糊集理论，对模糊集的法则与系统化加以定义，并将此理论用于描述模糊现象。在涉及决策方面的问题时，人们往往不能掌握全面的、直接的信息，这就使得决策环境更复杂，存在着不确定性，而随着模糊集的提出，人们渐渐发现模糊集可以通过隶属度来反映所需信息，基于此，各领域学者对其方法进行了深入研究。1986 年，Atanassov K T［51］通过众多学者在模糊数学领域的研究，在模糊集的基础上，改进了传统模糊集只考虑隶属度这一个方面的缺陷，提出了直觉模糊集（IFS），将隶属度拓展为隶属度、非隶属度和犹豫度三个度量标准。但直觉模糊集局限于隶属度与非隶属度之和小于等于1 的情况，对于其大于1 时并不适用，决策受到限制。为此，美国研究模糊理论的专家提出了毕达哥拉斯模糊运算，虽然隶属度与非隶属度之和大于1，但其平方和仍小于等于1，他将此定义为毕达哥拉斯模糊集，这使得隶属度的取值更为广泛，应用这种方法的学者们无须修改原有的隶属度即可做出决策。在处理多属性决策问题时，毕达哥拉斯模糊集更能体现其应用广泛的特点。近年来，关于毕达哥拉斯模糊集的研究不断深入，衍生出了一系列与其他数学理论模型相结合的方法，如曾守桢等［1］提出了基于混合加权距离的毕达哥拉斯模糊TOPSIS 多属性决策方法研究等。

（三）文献述评

综上可以看出：现有评价大都采用传统单一的评价模型，并未从工具角度进行多方位结合；同时现有评价研究缺乏系统性研究范式，鲜有对山东省进行时空双维的实证评价；毕达哥拉斯模糊TOPSIS法在模式识别、区域生态环境评价、多属性群决策方法、信息度量等方面得到广泛的应用，但在管理、区域经济等领域还处于发展阶段，毕达哥拉斯模糊集的应用还有待进一步拓展，基于混合加权距离的毕达哥拉斯模糊TOPSIS法在区域创新等方面的研究更是鲜有。基于此，本文从指标体系的初步构建、优化完善到运用混合加权距离的毕达哥拉斯模糊TOPSIS 法对山东省17 地市进行区域创新能力进行时空双维度的实证评价，形成了系统的研究范式，旨在为同领域专家的研究做出补充与借鉴，为区域创新政策的制定提供参考，具有一定的理论贡献与实践指导意义。

三、模型构建

（一）DPSIR模型

DPSIR 模型是构建评价指标体系的经典模型，文章借鉴前人研究［52］，以技术创新能力为目标层，从驱动力、压力、状态、影响和响应五个方面设置准则层，准则层下分别设置不同数量的要素层：“驱动力”下设置经济发展、社会生活、教育水平；“压力”下设置环境压力、社会压力；“状态”下设置创新投入、创新环境；“影响”下设置创新产出；“响应”下设置经济响应、环境响应、科技响应。

（二）指标回路法

指标回路法是从因子分析法中引申出，对指标体系进行优化、完善的模型，其主要包含三个步骤，即指标间相关性筛选、单个指标鉴别力筛选及整体指标体系的合理性验证。通过相关性筛选可以筛除相关性较大的指标，通过鉴别力筛选可以筛除指标贡献度不足的指标，最后通过合理性验证，形成最终的指标体系［53］。

1.相关性筛选的模型构建

相关性是两个指标或多个指标相关性较大，对上一级评价客体的贡献度存在交叉的情况，为保证指标体系的简洁性进行筛除。文章借鉴前人研究［53］，采用R系数进行测度，并以R＝0.65 进行筛选，见公式（1）：

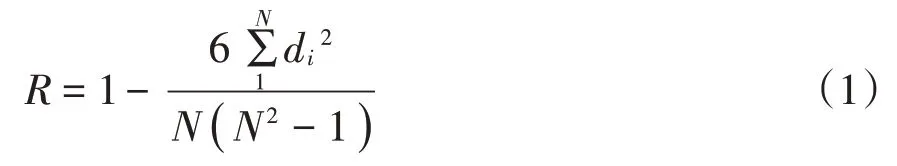
其中，di为变量值差，即xi-yi，i＝1，2，…，N，N为次数。

2.鉴别力筛选的模型构建

鉴别力是指单个指标对上一级评价客体的贡献度，为保证指标体系的有效性，对于贡献度不足的指标进行筛除。文章借鉴前人研究［53］，采用差异系数来描述评价指标的鉴别力，差异系数用标准差相对于平均数大小的相对量来表示，见公式（2）：

其中，CV为变差系数；s为标准差；x为平均值。

3.合理性验证的模型构建

合理性验证是对整个指标体系的完整性、贡献度等进行测度，是指经过相关性、鉴别力筛除后的最终指标体系相对于初步构建的指标体系而言。文章借鉴前人研究［53］，采用因子分析对其合理性进行验证。设S为指标数据的协方差矩阵，借助协方差矩阵及协方差的迹对筛选后指标的信息贡献率In进行测算，见公式（3）：

其中，n、p分别为筛选之后、之前的指标个数。

（三）PFHWD-TOPSIS模型的构建

为了解决多目标多属性综合评价决策问题，考虑被调查对象的模糊和不确定性，毕达哥拉斯模糊集作为一种新的模型被广泛应用，它较传统模糊集和直觉模糊集而言更为灵活，适用范围更为广泛，弥补了直觉模糊集其隶属度与非隶属度之和可能大于1 这一缺陷。同时，这一领域众多学者对此模型加以改进，提出了基于混合加权测度的毕达哥拉斯模糊TOPSIS 模型，此模型在毕达哥拉斯有序加权距离（PFOWD）的基础上，研究了权重所带来的影响，提出了毕达哥拉斯模糊混合加权距离（PFHWD），并将其与TOPSIS 法相结合（PFHWD-TOPSIS），用于解决信息存有模糊性与不确定性的多属性决策问题。这一模型能有客观有效地反映出多指标下研究对象的实际情况。

定义1：毕达哥拉斯模糊集。

设X为论域，则为论域X上的毕达哥拉斯模糊集，μA(x)称为X中的元素x属于毕达哥拉斯模糊集A的隶属度；υA(x)称为X中的元素x属于毕达哥拉斯模糊集A的非隶属度，其满足

定义2：毕达哥拉斯模糊数与毕达哥拉斯模糊矩阵。

在处理多属性决策问题时，假设有m个研究目标和n个评价指标为可行方案集为评价属性集，权重向量为，该权重向量满足和

定义3：得分值函数。

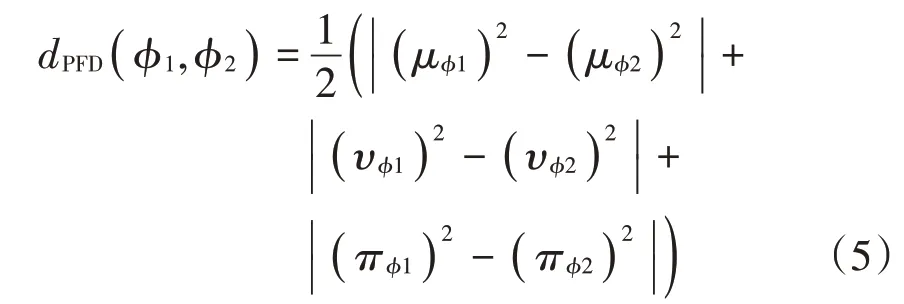
基于混合加权距离的毕达哥拉斯模糊TOPSIS法步骤如下［1］：

（1）由模糊数来构造毕达哥拉斯模糊矩阵。毕达哥拉斯模糊矩阵，其中cj(xi)=为方案集中在评价属性集中下的评估值。

（2）计算毕达哥拉斯模糊正理想解和负理想解。令正理想解为X+，负理想解为X-，其计算公式分别如下：

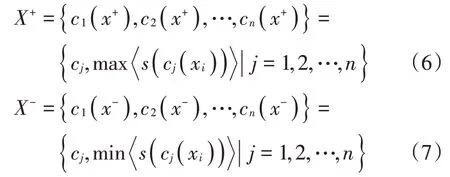
（3）分别计算各项方案与正理想解和负理想解的混合加权距离。PFHWD和PFHWD分别表示方案与步骤（2）求得的正理想解X+和负理想解X-的混合加权距离，其计算公式（8）如下：

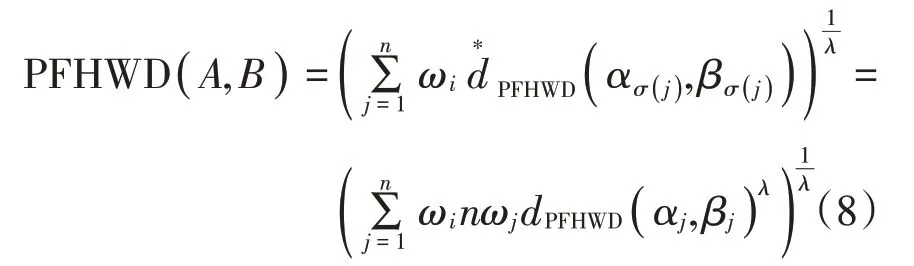
（4）计算方案的贴近度。在使用混合加权距离测度时，若使用传统贴近度的计算方法时往往会出现某个方案不能同时满足与正理想解最近和与负理想解最远的情况，因此相关领域的学者提出了一种新的计算方案xi的贴近度函数见公式（9）：

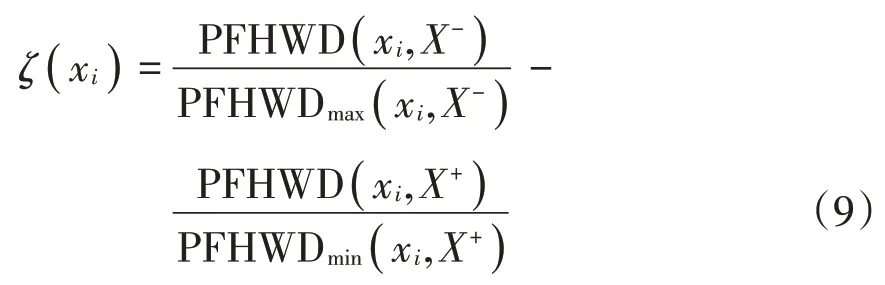
四、实证分析与讨论

（一）指标体系的初步构建

本文在前人研究的基础上运用DPSIR 模型构建的初步指标体系见表1所列。

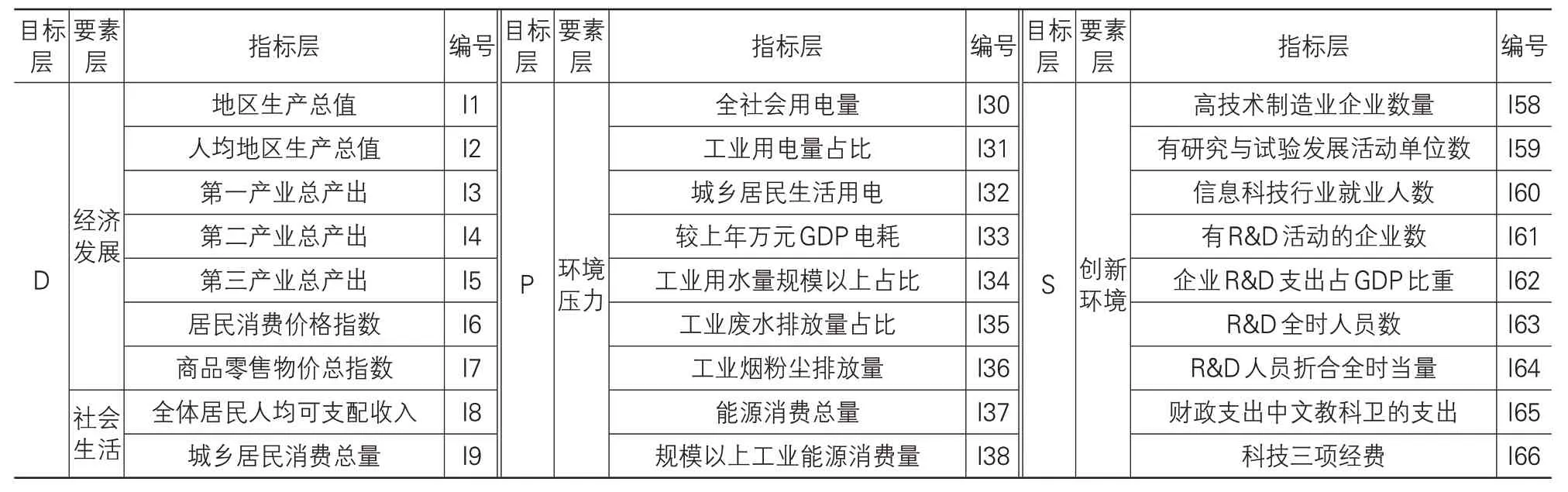
表1 山东省区域创新能力初步指标体系

续表1

（二）指标体系的优化

文章运用指标回路法［53］，选取山东省2018 年面板数据对初步构建的指标体系进行优化，通过相关性筛选，删除16 个指标，通过鉴别力删除15个指标，最终保留余下的55 个指标形成最终的指标体系，经指标体系合理性验证，合理性为99.3%，通过验证。山东省区域创新能力最终指标体系见表2所列。

（三）数据初步处理与权重确定

文章采用规范化方法（min-max 标准化）对初步取得的数据进行标准化处理［53］，运用熵值法进行赋权，鉴于规范化方法与熵值法均属于本领域非常成熟经典的模型，故在此不多做介绍。具体指标权重见表2所列。

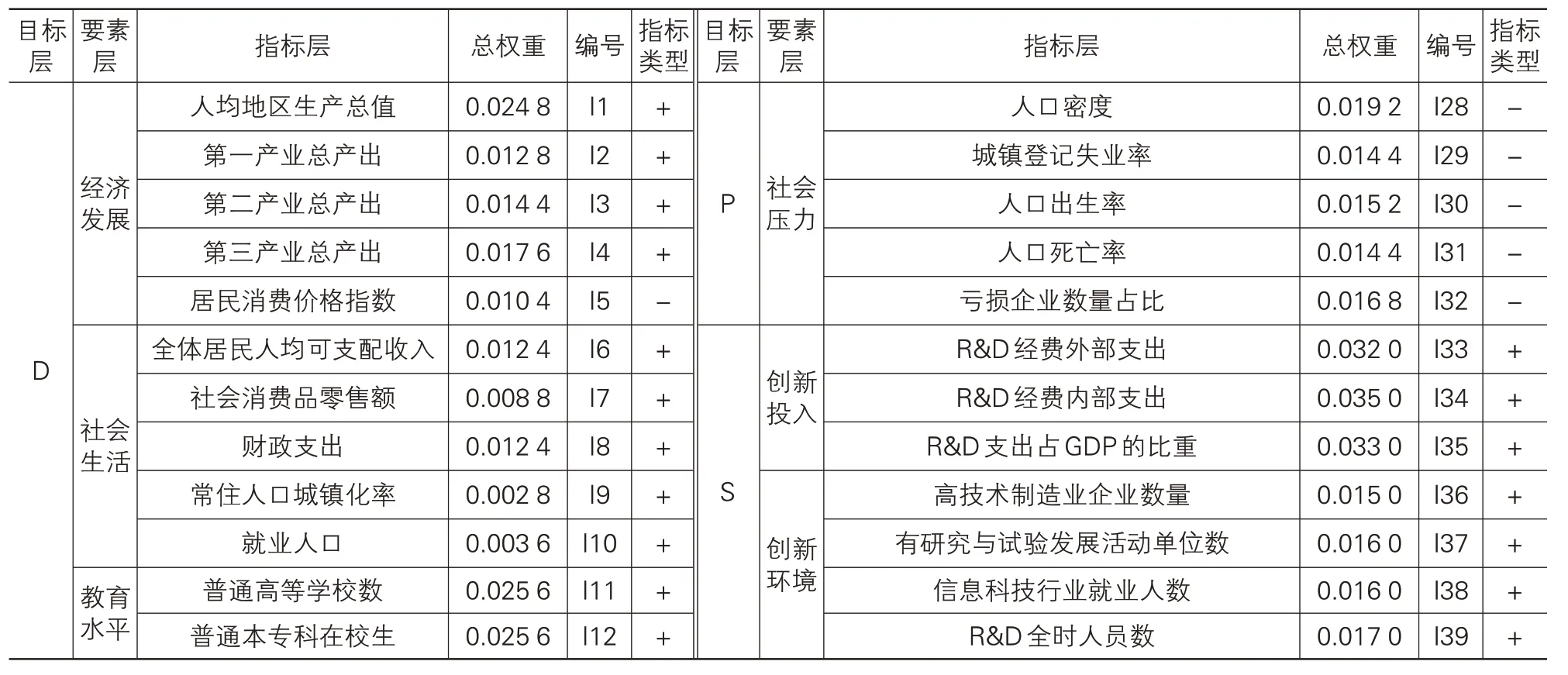
表2 山东省区域创新能力最终指标体系

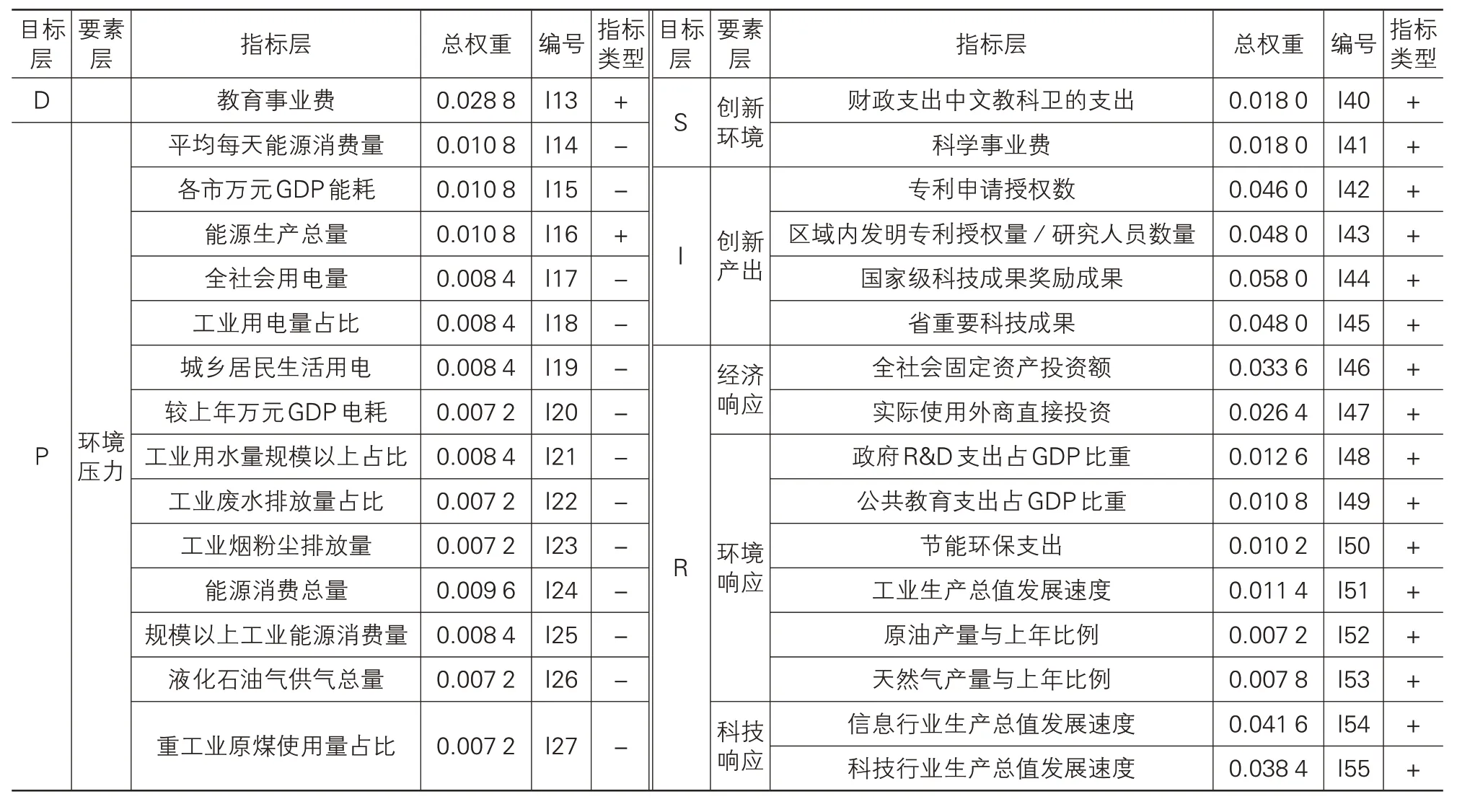
续表2

（四）山东省区域创新能力的时空双维实证评价

（1）构造毕达哥拉斯模糊矩阵。利用毕达哥拉斯模糊的方式来对2018 年山东省17 地市55 个评价指标数据进行分析，并构造出17×55的毕达哥拉斯模糊矩阵（鉴于篇幅限制，矩阵仅留存备索）。

（2）计算毕达哥拉斯模糊正理想解和负理想解。根据步骤（1）得出的毕达哥拉斯模糊矩阵，利用公式（1）计算出2018 年各市区得分值sφi（i=1，2，…，17），并结合公式（3）和公式（4）计算毕达哥拉斯模糊正理想解X+和负理想解X-：

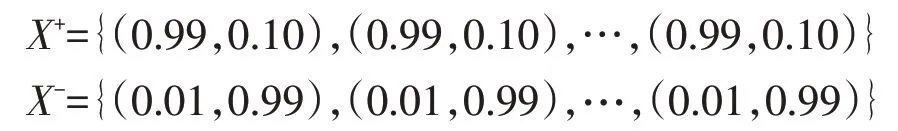
（3）分别计算方案与正理想解和负理想解的混合加权距离。已知权重向量ωi( )i=1,2,…,55 ，设λ=2，利用混合加权距离公式（5）算出17地市与正理想解X+和负理想解X-的混合加权距离和PFHWD

（4）计算贴近度。利用公式（6）分别计算17地市的贴近度由步骤3、步骤4可得基于PFHWD-TOPSIS 方法的2018 年山东省17地市区域创新能力评价结果，见表3所列。

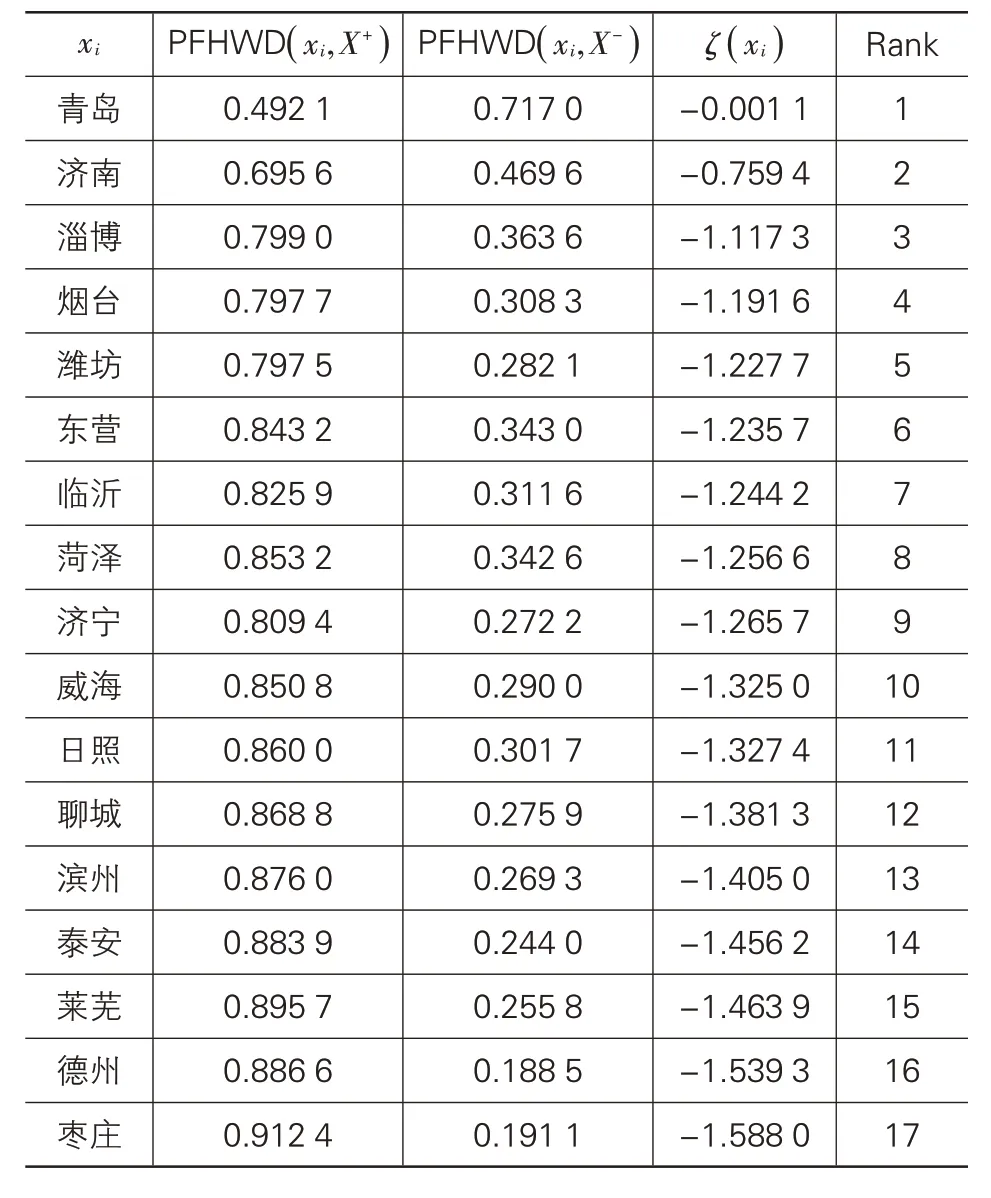
表3 2018年山东省17地市区域创新能力评价贴近度

（5）根据贴近度大小对17地市进行择优排序。贴近度ζ(xi)越大，结果越优，区域创新能力越强。其贴近度由大到小排序结果见表3所列、图1所示，并运用ARCGIS软件绘制可视化图如图2所示。

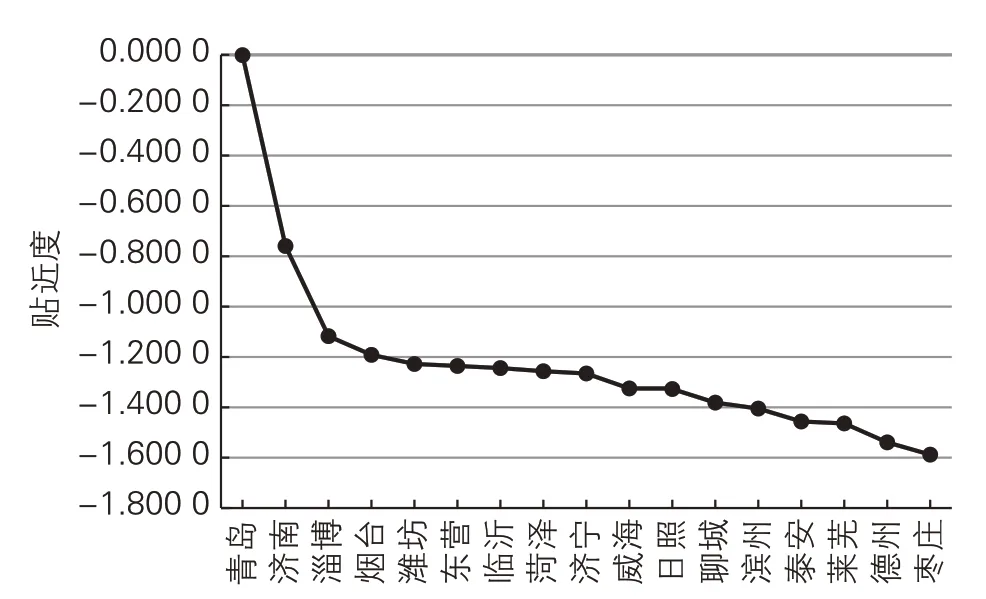
图1 2018年山东省17地市区域创新能力折线图

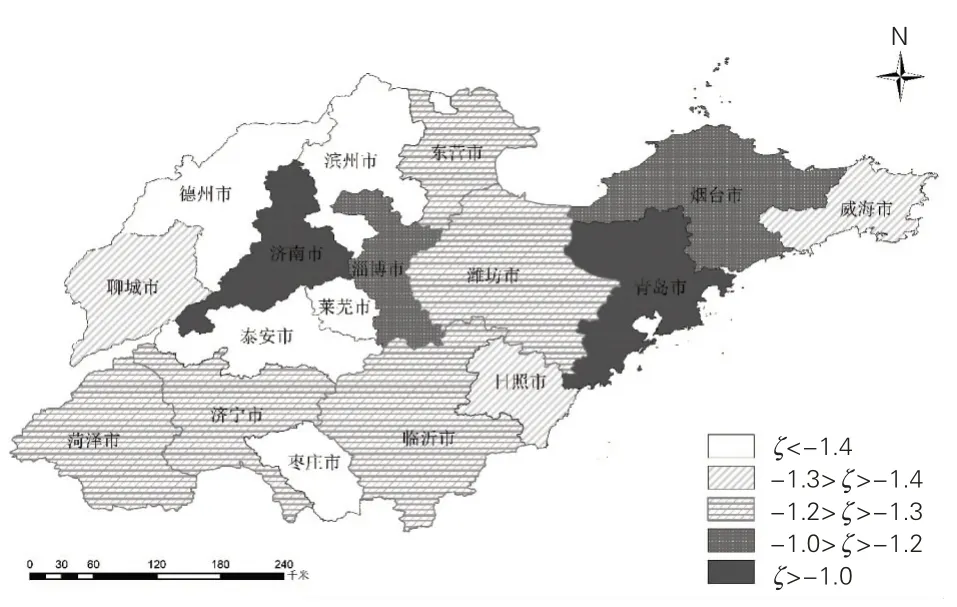
图2 2018年山东省17地市区域创新能力空间分异

重复步骤1-步骤5，同理可得2009-2017 年山东省17 地市区域创新能力评价结果，结合2018 年结果进行综合，具体见表4 所列，如图3所示。

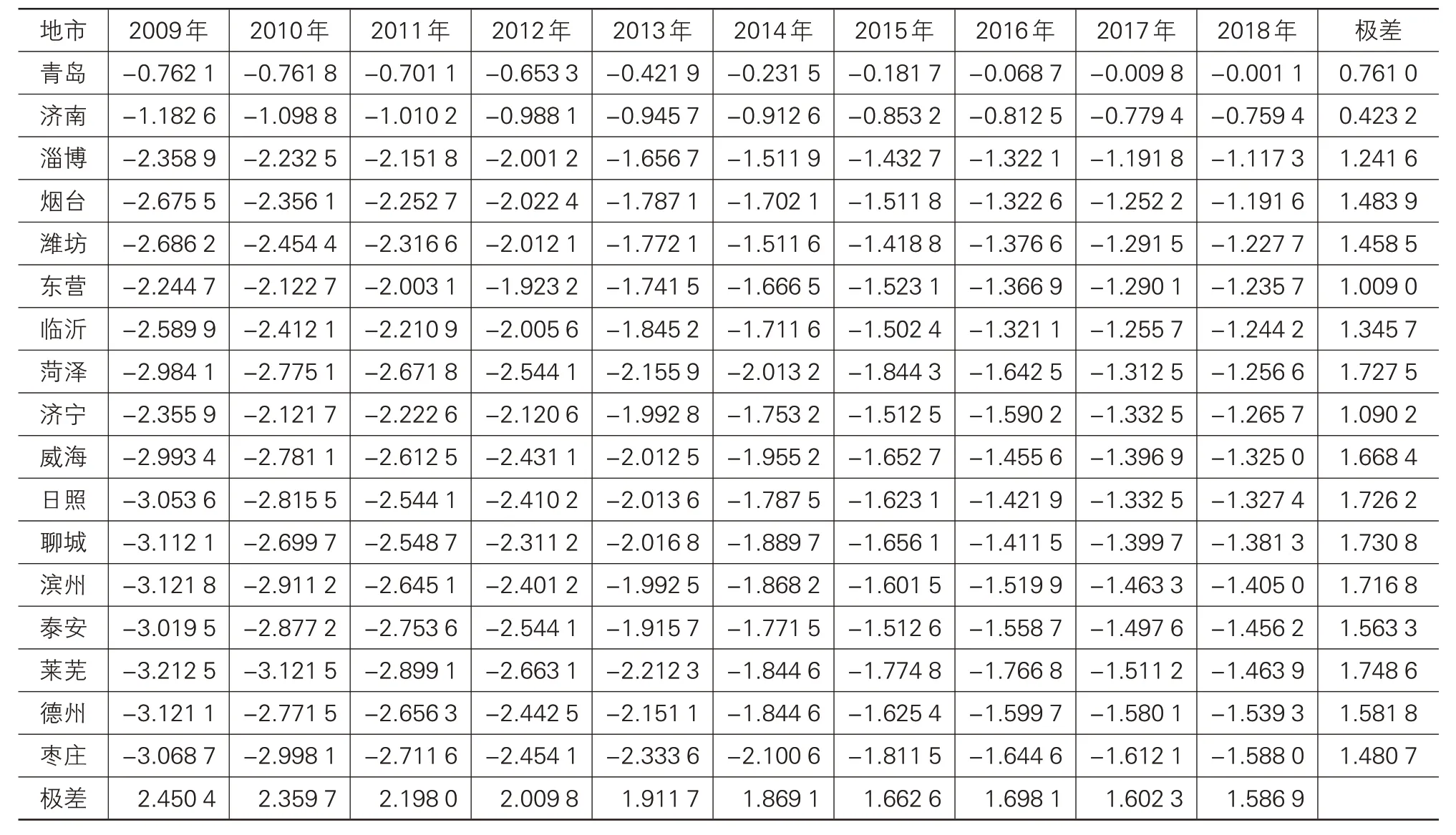
表4 2009-2018年山东省区域创新能力评价结果

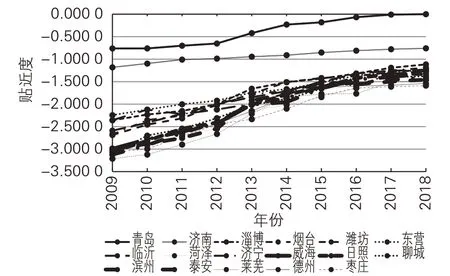
图3 2009-2018年山东省17地市区域创新能力折线图

（五）结果讨论

通过对2009-2018 年山东省17 地市区域创新能力的时空双维实证评价，可以得出时间和空间两个维度的评价结果，结合PFHWD-TOPSIS 模型中参数λ的设置对区域创新能力评价贴近度函数ζ的影响，本文从以下三个方面进行结果讨论。

1.2018年山东省区域创新能力分析

（1）通过表3、图1 可以看出：2018 年山东省17地市区域创新能力排序为青岛、济南、淄博、烟台、潍坊、东营、临沂、菏泽、济宁、威海、日照、聊城、滨州、泰安、莱芜、德州、枣庄。区域创新能力排名首位的青岛（-0.001 1）与末位的枣庄（-1.588 0）的极差为1.586 9，说明2018 年山东省17 地市区域创新能力仍存在较大差距；首位青岛与排名第二位济南的差距为0.758 3，济南与排名第三位淄博的差距为0.357 9，而淄博与末位枣庄的差距仅为0.470 7。这充分说明青岛、济南的区域创新能力不仅居全省前两位，且远超全省区域创新能力的平均值（-1.222 7）。

（2）从现有山东半岛城市群“两圈四区”格局来看，青岛都市圈（青岛、潍坊）的区域创新能力均值为-0.614 4，济南都市圈（济南、德州、聊城、泰安、淄博、莱芜）的区域创新能力均值为-1.286 2，东滨都市区（东营、滨州）的区域创新能力均值为-1.320 4，烟威都市区（烟台、威海）的区域创新能力均值为-1.258 3，临日都市区（临沂、日照）的区域创新能力均值为-1.285 8，济枣荷都市区（济宁、枣庄、菏泽）的区域创新能力均值为-1.370 1。通过对“两圈四区”格局区域创新能力的分析可以看出，青岛都市圈仍居首位，且远高于第二位的烟威都市区，随后依次是临日都市区、济南都市圈、东滨都市区、济枣荷都市区，济南都市圈排名第四位，较济南在17地市的排名第二位差距较大。因此，济南市应在注重自身区域创新能力提高的同时，要更加注重对周边济南都市圈地区创新要素的流动与带动，促进山东省区域创新能力的共同提升。

2.2009-2018年山东省区域创新能力分析

（1）通过表 4、图 3 可以看出，2009-2018 年山东省17 地市区域创新能力均呈稳步上升态势，但增长幅度存在差异，这可以从时间序列的极差指标来体现。2009-2018 年，山东省17 地市增长幅度最大的是莱芜市，增长了1.748 6；增长幅度最小的是济南市，增长了0.423 2。按增长幅度大小顺序依次为莱芜、聊城、菏泽、日照、滨州、威海、德州、泰安、烟台、枣庄、潍坊、临沂、淄博、济宁、东营、青岛、济南，此顺序与2018 年区域创新能力排名大致相反，说明山东省区域创新能力的平均水平在不断增加，尤其是区域创新能力较弱的地市增长较快。

（2）从时间横截面极差上可以看出，2009 年山东省17 地市区域创新能力的极差为2.450 4，2018年则下降到1.586 9，说明10 年间山东省17 地市区域创新能力空间上仍存在差距，但差距在逐步缩小；与此同时，可以发现山东省17 地市在2012-2014年都有明显提升，这与我国创建创新型国家、区域创新投入的增加成正相关。

3.参数λ对贴近度函数ζ的影响分析

在毕达哥拉斯模糊TOPSIS方法中使用混合加权距离测度时，可以发现随着参数λ 的变化，相对应的贴近度函数也会发生变化，得出不同的贴近度从而影响择优排序。对于本文而言，当λ取值不同时，研究对象所对应的区域创新能力排名也会受到影响，运用 MATLAB 绘制参数λ对贴近度函数ζ的影响如图4所示，反映了对2018年山东省区域创新能力评价时，参数λ 对贴近度函数ζ的影响。可以看出，当λ＝1.5时和当λ＝2时，贴近度函数图像出现了明显的变化；当λ＝2.5和λ＝3时，贴近度函数图像有较小变化；当λ≥4.41时，贴近度函数图像排名趋于稳定。其对应的区域创新能力排名见表5所列。

图4 参数λ对贴近度函数ζ的影响

表5 参数λ对贴近度函数ζ的影响

参数λ的取值在［1.5，2］区间内对函数影响较大，故详细分析当λ由 1.5 变为2 时，可以看出λ的取值对于1-6名（依次为青岛、济南、淄博、烟台、潍坊、东营）以及11-17 名（依次为日照、聊城、滨州、泰安、莱芜、德州、枣庄）影响不大，而对于7-10 名的影响较为明显：菏泽排名由第7到第8下降1位；威海排名由第8 到第10 下降2 位；临沂排名由第9到第7上升2位；济宁排名由第10到第9上升1位。综合来看，参数λ 的取值对于青岛、济南、淄博、滨州、泰安、烟台、枣庄这7 个城市影响不大，青岛排名第1，可视为2018年山东省区域创新能力最高地市；枣庄排名第17，其区域创新能力还有待提高。

在 PFHWD-TOPSIS 模型中，λ 取值的不同，所选取的加权距离也就不同。特别地，当λ＝1时，对应的毕达哥拉斯模糊混合加权距离（PFHWD）为毕达哥拉斯模糊混合加权汉明距离（PFHWHD）；当λ＝2 时，对应的毕达哥拉斯模糊混合加权距离（PFHWD）为毕达哥拉斯模糊混合加权Euclidean距离（PFHWED）。参数λ 的取值可以根据决策者的偏好进行调整，以便于结合不同的研究需要选择恰当的模型，以得出更加客观实际的决策结果。

五、结 论

本文改进传统经典TOPSIS 为PFHWD-TOPSIS，并将其运用到山东省区域创新能力的时空双维实证评价中来，研究主要得出以下结论：

（1）本文借鉴DPSIR 模型构建指标体系，引入指标回路法从指标相关性、鉴别力及指标体系合理性角度进行优化，形成了完善的区域创新能力评价指标体系；运用PFHWD-TOPSIS 进行山东省区域创新能力的实证评价，探讨了调节参数值λ的作用和灵活性，为同领域专家学者的研究提供了思路借鉴。

（2）从时间维度来看，青岛市区域创新能力始终处于山东省首位，山东省区域创新能力的平均水平在不断增加，整体差距在逐步缩小，尤其是区域创新能力较弱的地市增长较快；山东省17 地市在十八大以后区域创新能力均有着明显提升，这与国家、山东省的区域创新战略成正相关。

（3）从空间维度来看，青岛市、济南市在山东省17地市中排名居前两位，且远超省平均水平；济南市单独排名与济南都市圈在“两圈四区”中的排名差距较大，说明济南市应在注重自身发展的同时，更应促进济南都市圈内部科技创新要素流动，促进区域创新能力的共同提高。