超声波声场模拟及能量分布仿真研究

耿 帅 刘士伟 韩立斌 王 岩 董颖怀 程子政

（1、天津科技大学机械工程学院，天津300222 2、空军装备部驻辽阳地区军事代表室，辽宁 沈阳110000）

1 概述

随着超声波技术的迅速发展，其应用范围也越来越广泛，然而关于超声波的研究多为单振源声场模拟方面，而单一振源无法实现工业生产中某些复杂零件的清洗或是针对某一零件的多种处理方式[1]，故需要研究多源振动在液体介质中的超声能量场的分布，以实现复杂的工艺处理。关于多振源在液体介质中的超声能量场分布的研究对于工业生产具有十分重大的意义，可以大量节约人工成本、提高工件质量和生产效率。因此本文开展了相关方面的研究，期望能够建立多振源在液体介质中的超声能量场分布模型。这在超声应用如超声去毛刺、超声破碎等方面具有重要意义。

2 超声波声场能量分布模型

2.1 模型定义

超声波换能器通过振动使临近换能器面的介质在平衡位置附近作高频往复振动，由于介质之间互相影响而带动远处的介质运动，从而达到传播的目的[2]。已知超声波是一种正弦波，其运动方程的一般表达式为

本文选用了两种振源分布方案进行超声能量叠加的研究，如图1 和图2 所示。其中观测点距离两换能器中心点的距离均为r0。

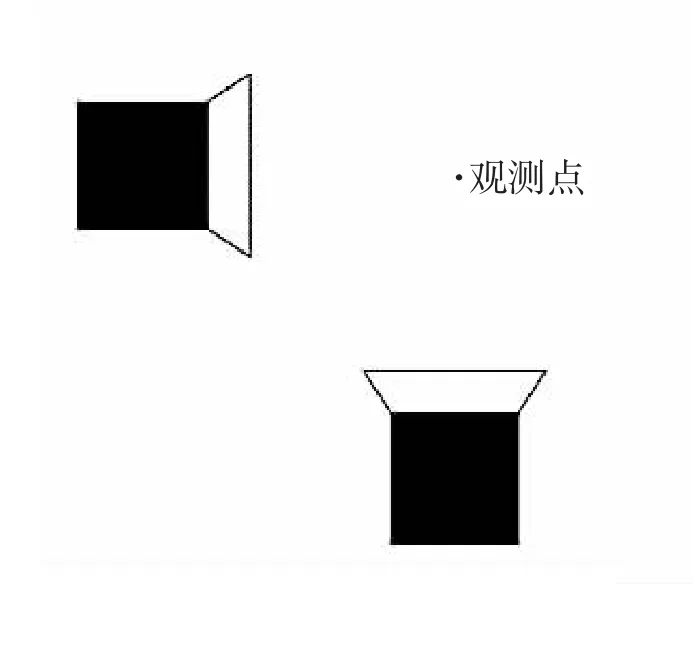
图1 振源分布方案一

图2 振源分布方案二

2.2 声强分析

已知声压表达式为[3]：

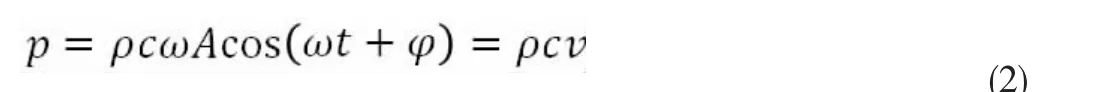
对于布置方案1，两换能器振动产生的超声波叠加后其角频率与初相位均未发生改变，而振幅变为原振幅的倍，故两振源产生的超声波叠加后声压也变为原声压的倍，即

两振源产生的超声波叠加后声强的计算公式为：

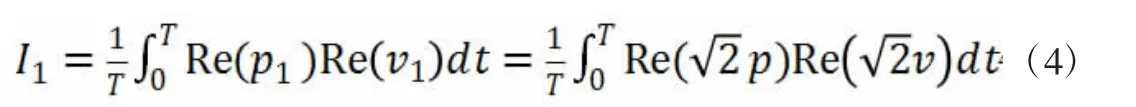
得出方案1 振源布置下观测点超声声强表达式为：

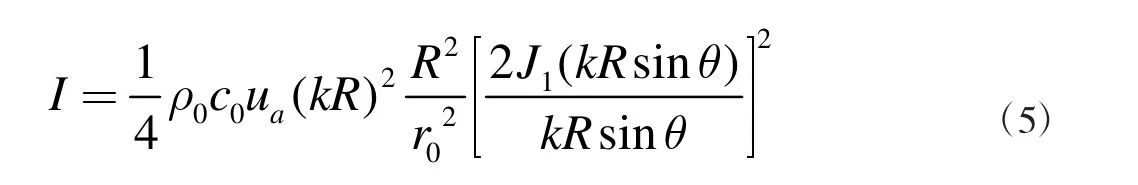
其中r0为观测点距换能器中心点的距离，由于观测点在中心轴线上，对比单源超声声场中距换能器中心为r0的观测点的声强，可以看出方案1 振源布置下，在相同位置产生的超声能量为单源布置的2 倍。

根据上文运动分析中关于两种振动叠加的研究，可以假设振源布置方案1 下超声场中任意位置观测点的声强为

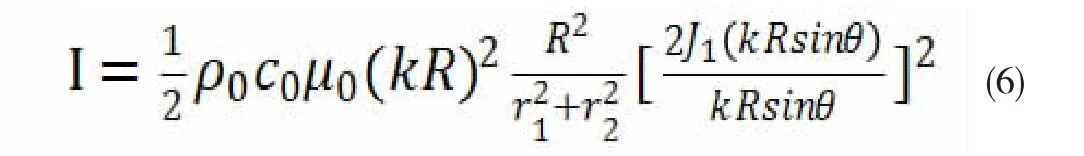
其中r1、r2分别为观测点到两换能器中心点的距离。

对于布置方案2，根据上文研究过程，速度幅值变为原来的2 倍，可得到观测点处声强表达式为

根据声强及速度的研究，假设振源布置方案2 下超声场中任意位置观测点的声强为：

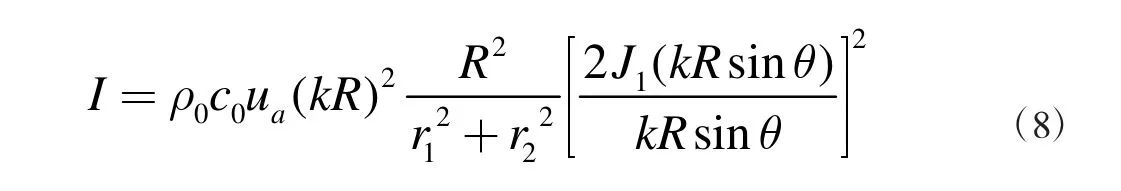
其中r1、r2分别为观测点到两换能器中心点的距离。

2.3 多源振动超声波声场模型

根据上文对于方案1 布置下声场分布的研究可知，两个换能器振动所产生的超声波叠加后，波的运动方程中仅有振幅发生改变，而换能器半径和功率、超声波频率等参数均未发生改变[4]，根据公式(5)，观测点的能量扩大为原来的2 倍，则可视作两振源形成了新的换能器，其在以观测点为原点所建立的直角坐标系中与y 轴夹角为45°，如图3 中虚线部分。根据上文对于方案2 布置下声场分布的研究可知，两个换能器振动所产生的超声波叠加后，波的运动方程中仅有振幅发生改变，而换能器半径和功率、超声波频率等参数均未发生改变，根据公式(5)，观测点的能量扩大为原来的4 倍, 而叠加后超声波方向与y 轴夹角并未发生改变，则可视作两振源形成了新的换能器，其在以观测点为原点所建立的直角坐标系中与y 轴夹角为0°，如图4 虚线部分所示。

图3 方案一超声波叠加

图4 方案二超声波叠加

根据公式(6)可知，叠加后形成的换能器在观测点处产生的声强为单源产生声强的2 倍，而根据上文对于运动分析的研究，方案1 和方案二布置下声场叠加后超声波频率f、换能器尺寸R、振速幅值ua均未发生改变，则判断声程r 发生改变，即新形成的换能器距观测点距离发生改变，而其余参数均未改变。根据几何关系可知观测点距新换能器中心点的距离为。

根据公式(6)，在Matlab 软件中建立了两种方案布置下声场能量的分布模型。设定距离新形成换能器声程为r=50mm,其能量分布如图5 和图6 所示。

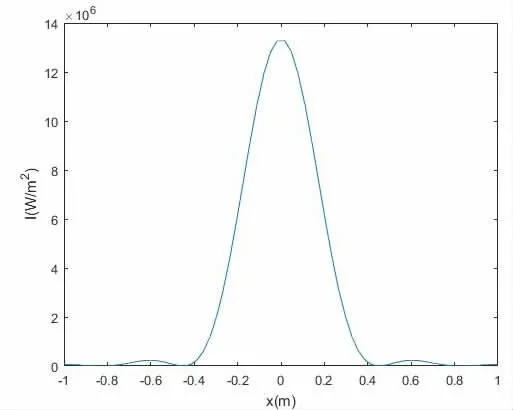
图5 方案一声程r=30mm 处声强分布

图6 方案二声程r=30mm 处声强分布

3 声场模拟在超声清洗中的应用

针对上文中的两种振源排布方案，我们建立相应的超声波清洗模型，清洗槽尺寸设为600 ,换能器类型为压电换能器。在COMSOL Multiphysics 中模型按照清洗槽的有效面积建立，液面最大高度为400mm,超声波换能器采用基本材料PZT-5H。在声-固耦合中，对水使用参考压力，温度定义为293.15K。

分别对两个方案中的振子排布方式进行声压场的仿真，在其它条件不变的情况下，改变超声频率，观察声压场的变化。

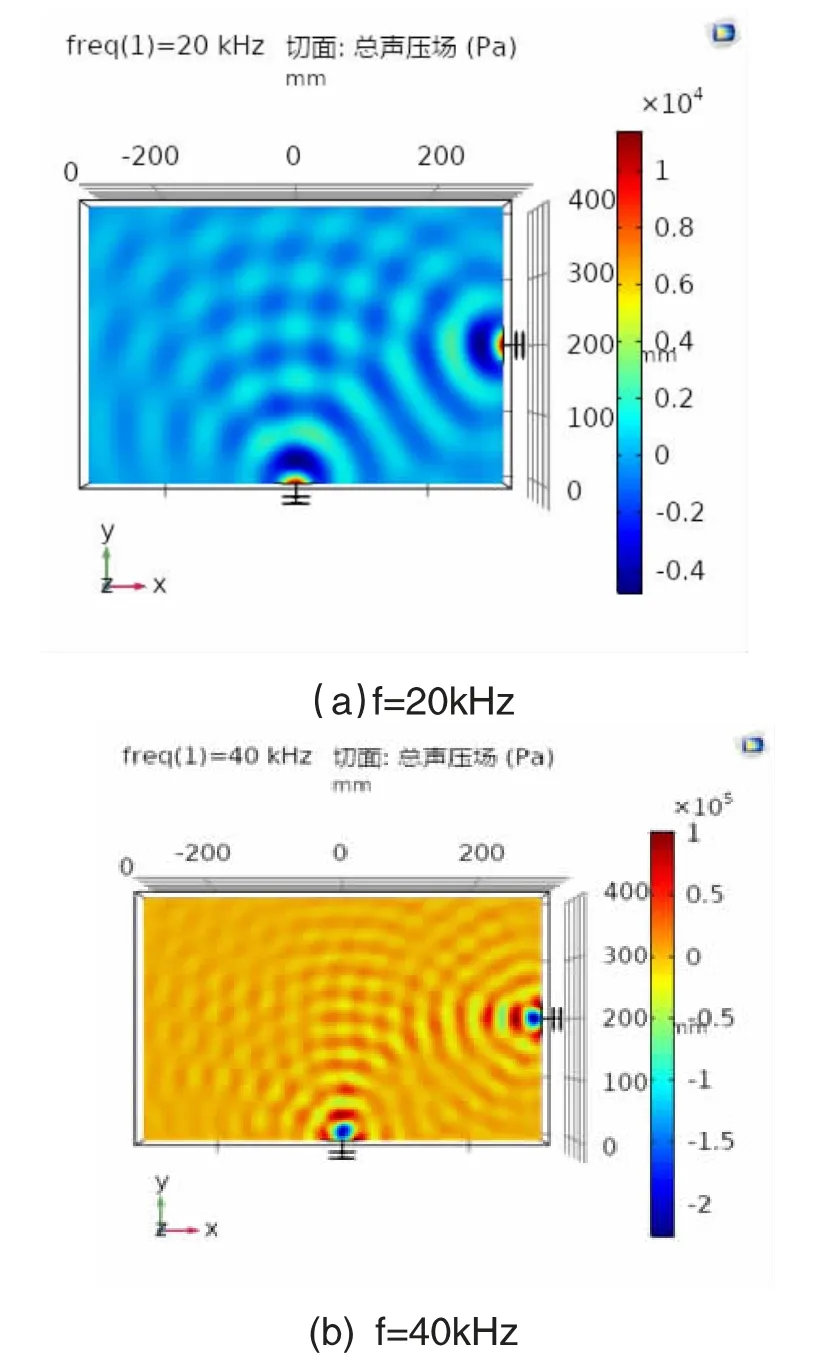
图7 方案一不同频率下的声压场

分别在超声频率为20kHz 和40kHz 的情况下，对方案一的声压场进行了分析，如图7 所示。声压总是在振子附近达到最大值，且在两换能器声波相交处的声压值高于其他地方。比较2个频率下的声压极值，可以看出40kHz 下的声压极值较大，达到1.01x105Pa。

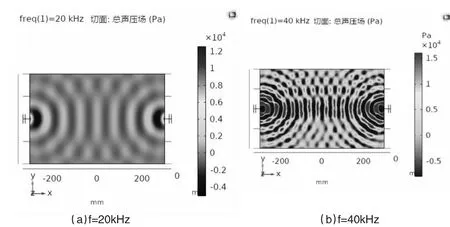
图8 方案二不同频率下的声压场

图8 对方案二分别在20kHz 和40kHz 情况下的声压场进行了分析，和方案一相同，声压最大值集中在振子附近，声波相交处的声压值高于其他地方，且在40kHz 下声压极值取得最大值1.15x105Pa。比较两种方案下的声压分布图，可以看出在超声频率为20kHz 的情况下，方案一的声压幅值与方案二的相差不大，但当频率增大到40kHz, 方案一的声压幅值远大于方案二的，这说明换能器的排布方式能够影响到超声清洗的声场分布[5]。实际上，声压并不是和超声频率成正比[6]，本文这只是针对超声场一种情况，超声清洗中超声振子不止两个，排布方式也有多种，想要让超声清洗场能量达到最高，需要更深的研究。

4 结论

4.1 设计了两种振源布置方案，对这两种方案下的声强表达式进行了理论推导。

4.2 根据两种布置方案运动的叠加与能量模型，绘制出两振源叠加后形成的新换能器在空间上的位置，以及其声场中指定声程处能量的分布状况。

4.3 针对两种振源布置方案，结合超声清洗的背景，对两种方案下的声压场和声压级进行了研究，实际上，超声声压场和频率并不是纯粹的正比关系，声压场受多种因素影响。