物流产业指标体系和评价模型的构建方法
赵宏伟, 张 帅, 荆学慧, 阮 莹, 张子祺
(沈阳大学 信息工程学院, 辽宁 沈阳 110044)
目前,我国还未确立一套衡量物流业发展水平的通用指标体系,所以对于指标的选取完全基于科学性、全面性、可行性原则和借鉴前人的实验研究指标.胡冰茜基于“资本增值”“供需”“资源”三个主要耦合动因、耦合因果路径构建了区域物流指标体系[1];年吕运根据物流的发展内涵,最终确定了城市经济发展水平、城市物流作业能力、城市物流基础设施、城市物流需求规模、城市物流信息化水平及城市物流人才培养6个一级指标,并逐一细化成24个二级指标[2];郭彩环通过选取物流产业增加值、河北省全社会固定资产投资和全社会就业人数作为指标,探讨了物流业对于经济发展的影响[3];王文柳将物流业指标总结为物流需求、物流供给和物流规模3个方面作为一级指标,再细划分为若干个二级指标,确保从各个方面整体分析物流业发展对于经济的影响[4];刘卜蓉等通过从区域经济发展、物流供给能力、基础设施和信息化程度方面构建指标体系,对物流发展水平进行综合评价研究[5].
综合指标的可理解性、数据可获得性以及考虑的全面性等,本文建立了以4个一级指标、12个二级指标为结构的我国物流业发展评价指标体系,详见图1.
一个国家或地区的经济发展状态能够通过很多指标进行衡量,例如人均GDP、GDP、三大产业增加值等,本文将GDP作为检验我国整体经济发展状态的指标,作为判断我国经济是否处在蓬勃发展期还是衰退期的首要依据[6].
1 数据来源
本文使用的数据来源于中华人民共和国国家统计局所发布的国民经济核算,依据数据的整体可得性最终选取2006—2019年数据进行分析[7],整理得到如下数据,见表1.
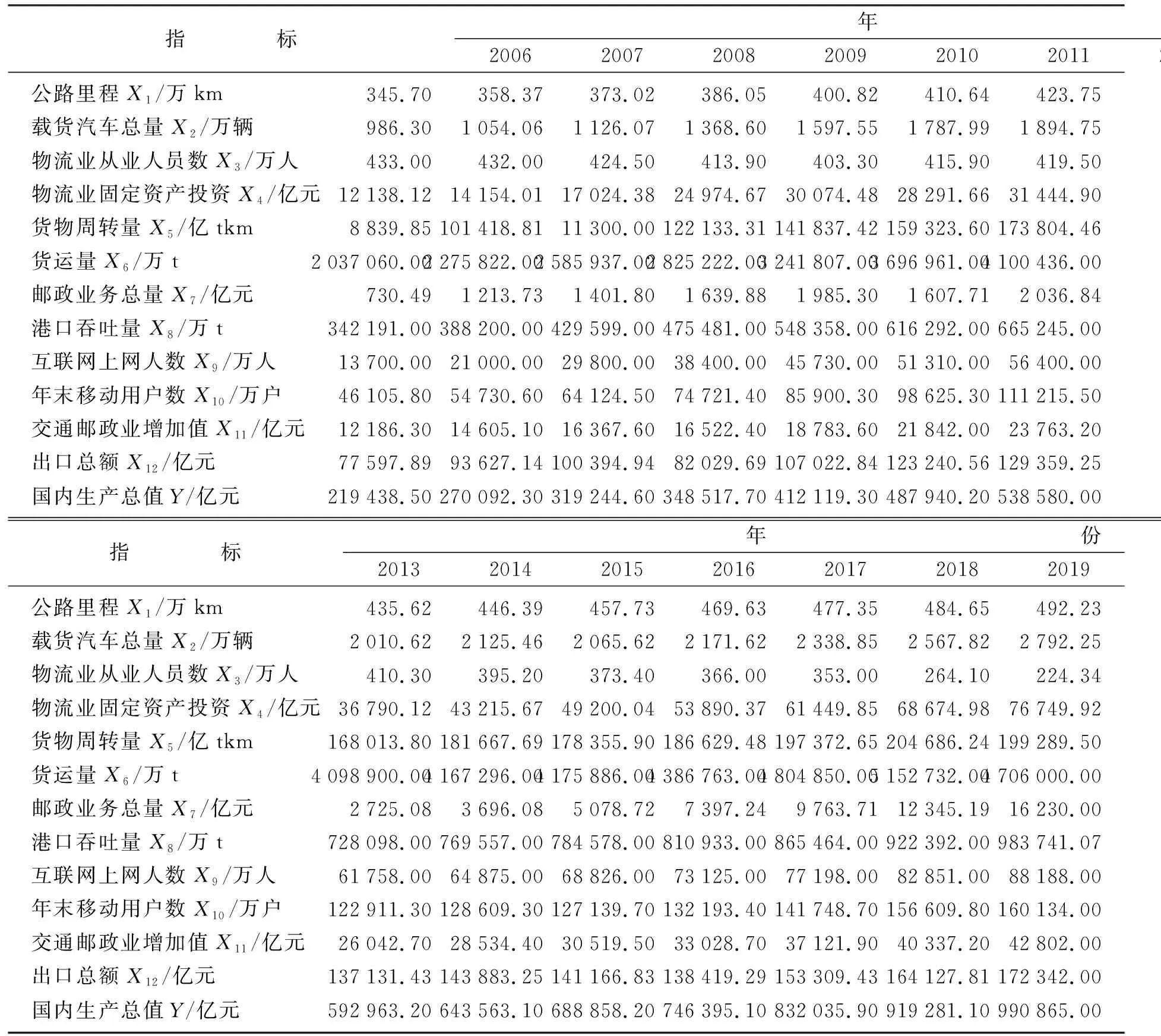
表1 我国物流业各项指标和GDP数据Table 1 Data of China’s logistics industry and GDP
目前由于中国统计年鉴数据不是很健全,对于未知数据利用近3年的平均增长速度推算得到[8].
2 物流指标筛选
实验分析过程中使用大量的指标,不仅会造成计算复杂、数据冗余等问题,指标间还会存在高度的相关度和重叠度.因此,本文将运用主成分分析法做因子分析对指标进行筛选,选出具有代表性的指标[9].筛选指标的过程如下.
2.1 数据标准化
不同指标具有不同的量纲和量纲单位,在选取因子分析法求解时若采用主成分法,由于主成分在通过总体协方阵求主成分时,常常最先考虑方差最大的指标,受到量纲单位的影响较大,就会导致出现不合理结果的现象.为了去除各个指标列中由于数据量纲不同带来的影响,前提是要对已选的各个指标的原始数据进行无量纲化处理.本文将选用Z-Score标准化方法,它不但可以完成大多数类型数据的标准化,也是很多分析工具默认的标准化方法[10].对原始数据做Z-Score标准化处理结果,详见表2.
2.2 KMO和Bartlett球形度检验
对标准化后的指标数据进行巴特利球形度检验和KMO(Kaiser-Meyer-Olkin)检验.KMO检验是通过分析变量之间的简单相关系数以及偏相关系数的大小,来判断是否适合做因子分析,取值大小在0到1之间,检验值越接近1越说明适合做因子分析;Bartlett检验是用来判断数据是否取自于服从正态分布的总体,若检验对应的统计值在显著性水平下显著,则可以进行下一步的分析.通过分析结果可知,KMO的检验值为0.81,可以判断利用这些指标很适合做因子分析;Bartlett球形检验的显著性为0,符合正态分布假定,相关系数矩阵与单位矩阵之间存在显著性差异,详见表3.

表3 KMO和Bartlett球形度检验Table 3 KMO and Bartlett sphericity test
2.3 提取主成分
经过前面检验已满足做因子分析的条件,需要对主成分进行提取.通过主成分抽取法对数据进行处理,得到总方差解释,见表4.
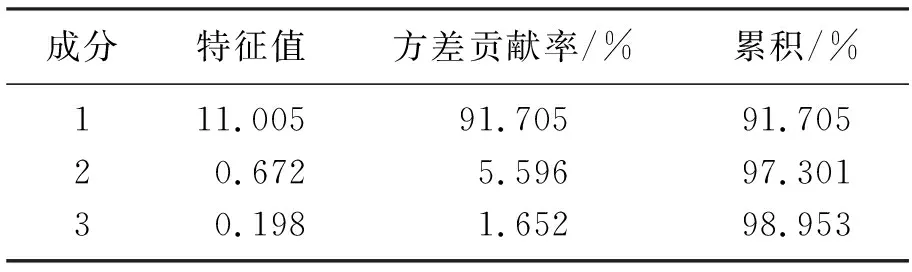
表4 总方差解释Table 4 Explanation table of total variance
由表4可知,成分1的特征值为11.005且方差贡献率为91.705%,成分2的特征值为0.672,小于1.0且方差贡献率为5.596%,成分3的特征值为0.198,小于1.0且方差贡献率为1.652%,越往后特征值越小,方差贡献率越小,故只选取成分1.
2.4 成分矩阵
图2(见封3)展示的是成分1因子负载绝对值,由南丁格尔玫瑰图可知,港口吞吐量指标的因子负载绝对值为0.995位列第一且为红色,判定它是物流发展需求的子指标;载货汽车总量的因子负载绝对值为0.993位列第二且为橙色,判定它是物流资源供给的子指标;交通邮政业增加值的因子负载绝对值为0.991位列第三且为黄色,判定它是物流发展效益的子指标;年末移动电话用户数的因子负载绝对值为0.990位列第四且为绿色,判定它是物流信息化水平的子指标.前四个指标分属于不同的一级指标,由此将港口吞吐量、载货汽车总量、交通邮政业增加值以及年末移动电话用户数4个指标作为代表性指标进行实验的研究.
3 多元回归模型
3.1 模型概述
1) 模型一般形式.
多元线性回归分析的基本思想是确定因变量和影响因变量的多个自变量之间的关系,通过求解未知参数实现对因变量的计算[11].设被解释变量y,x1,x2,…,xn为影响被解释变量变化的n个解释变量,线性回归模型为
y=β0+β1x1+β2x2+…+βnxn+ε.(1)
当n=1时,把式(1)称为一元线性回归模型;当n>2时,把式(1)称为多元线性回归模型.式(1)中ε称为误差项随机变量,β0,β1,β2,…,βn是n+1个未知参数,β0称为回归常数,β1,β2,…,βn称为偏回归系数,由此确定了被解释变量与解释变量之间的线性关系.
2) 模型参数估计.
利用收集的样本数据估计多元回归模型的参数,最小二乘法是模型参数估计中最常用的方法之一,也是最经典的估计方法.

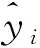
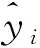
为了使离差平方和达到最小值,β0,β1,β2,…,βn应满足下述方程组
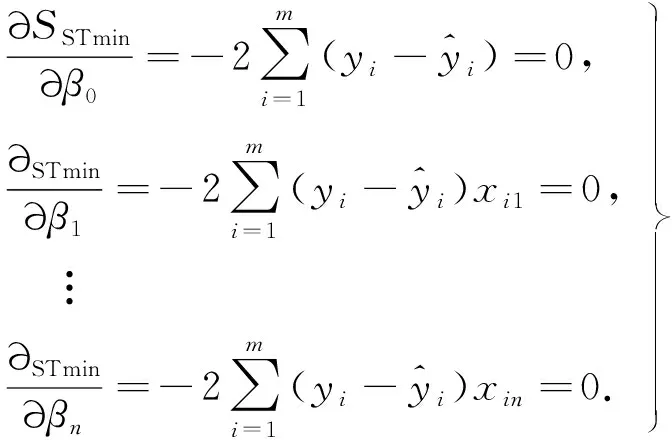
式(6)为n+1个方程,称为正规方程组.将式(4)代入式(6)得
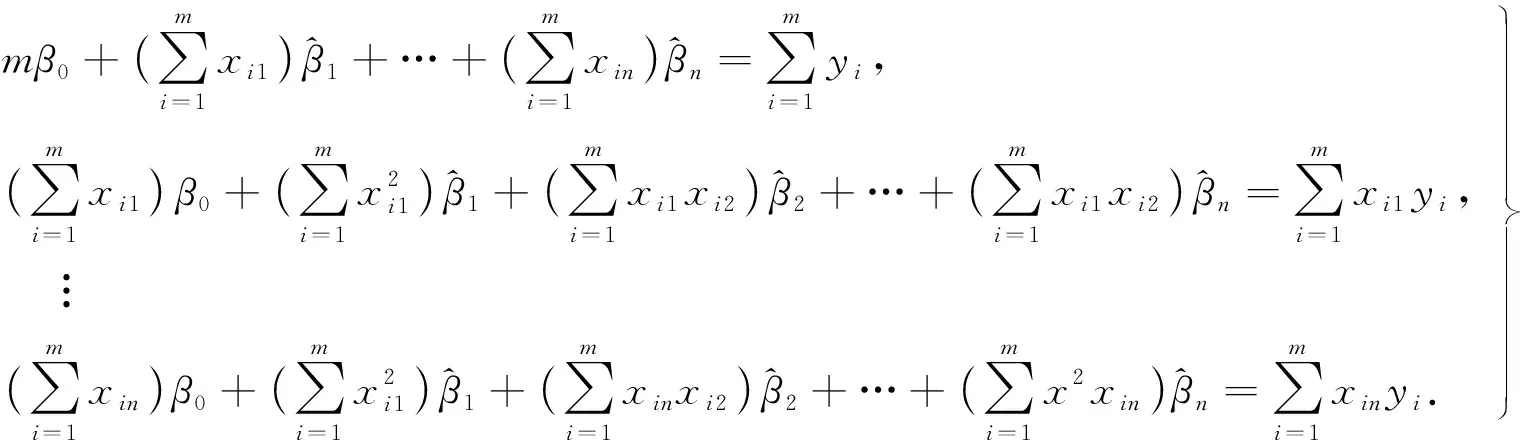
令
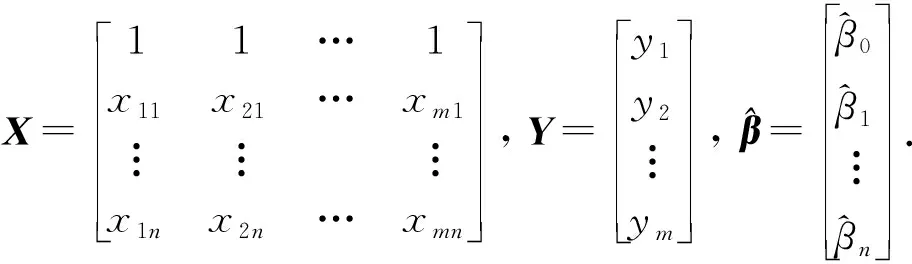
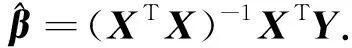
3) 模型检验.
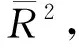
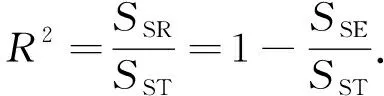
调整后的拟合优度为
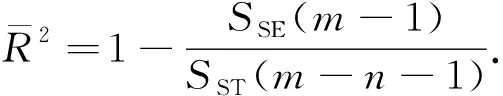
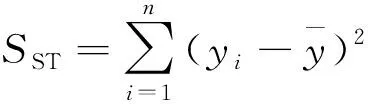
② 回归方程整体显著性检验,它是检验模型中被解释变量之间与解释变量之间的线性关系在总体上是否显著,也就是检验方程中的参数是否显著不为0.设原假设H0β1=β2=…=βn=0,备择假设H1βi(i=1,2,…,n)不全为零.在原假设H0成立的条件下,统计量F服从第一自由度为n和第二自由度为(m-n-1)的分布,构建F统计量得

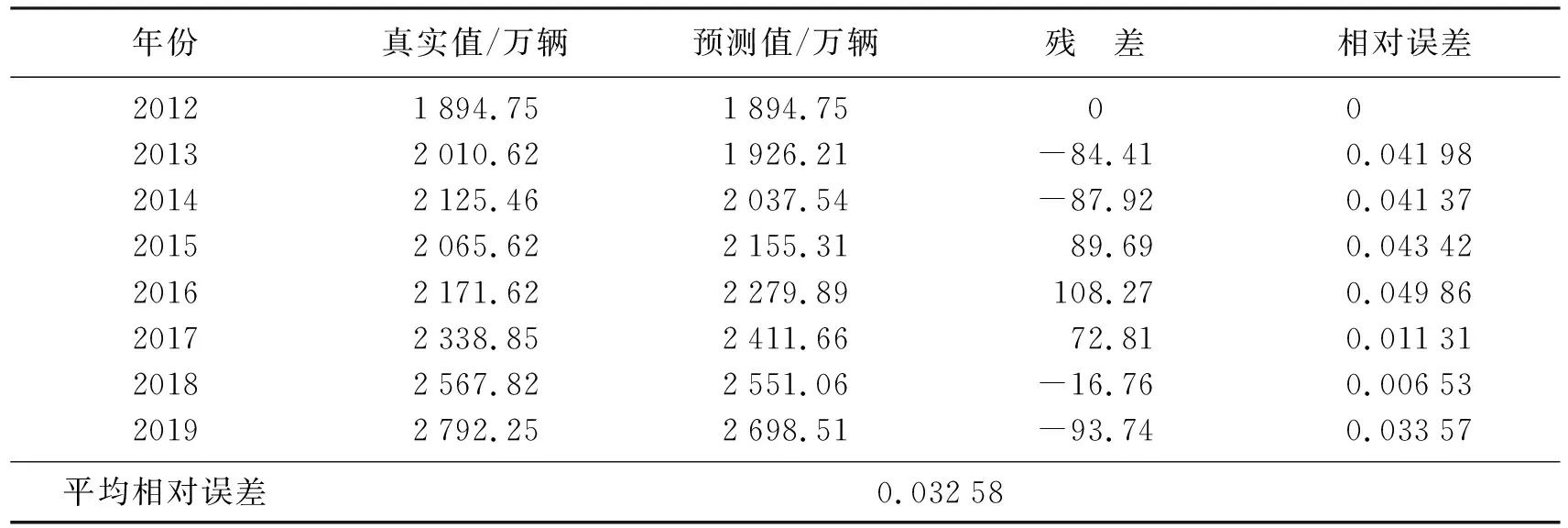
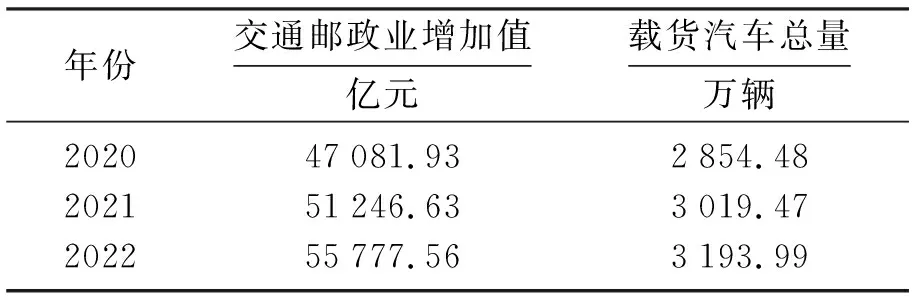
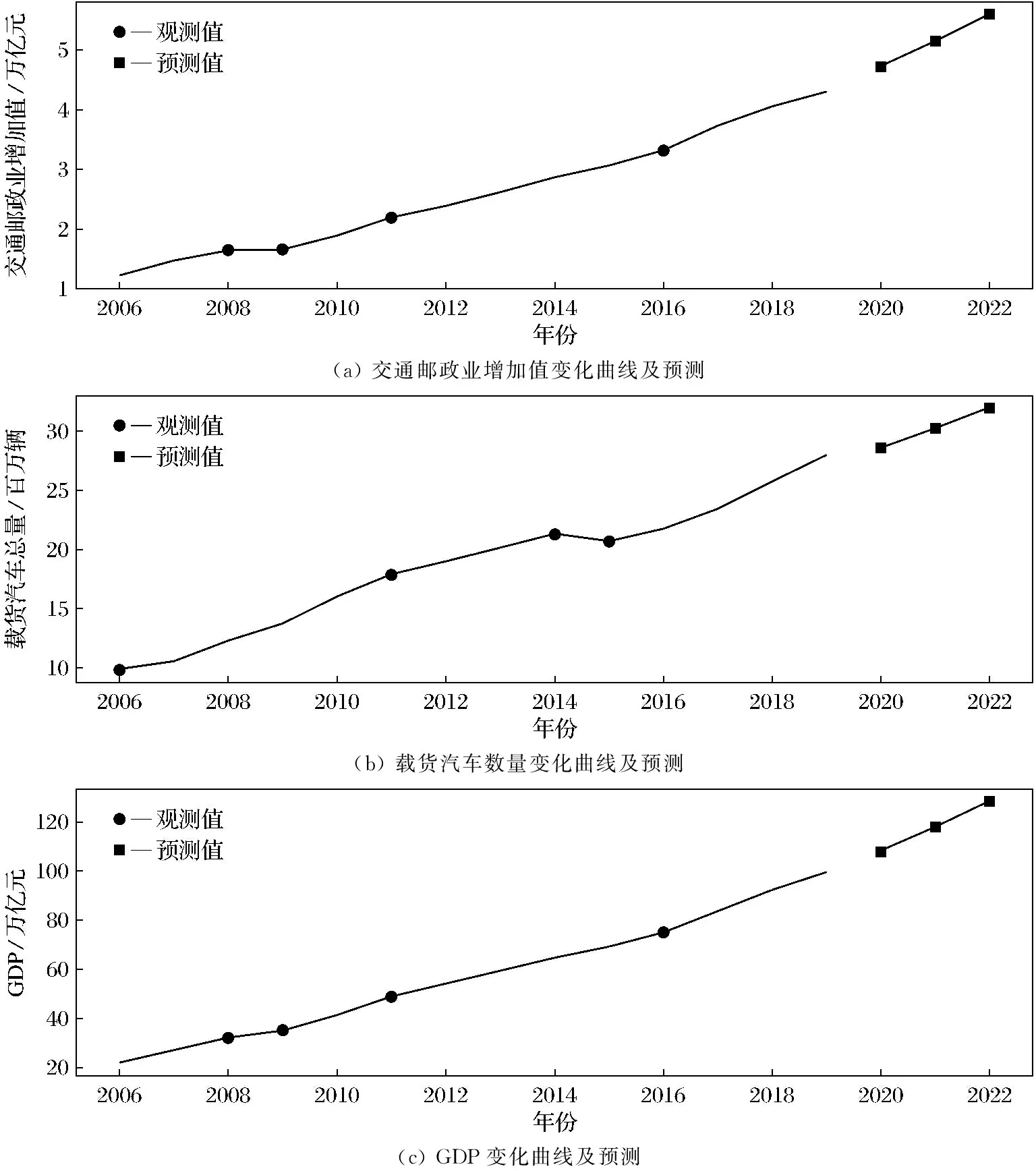
在指定显著水平α下,根据查统计学F分布表可知Fα(n,m-n-1)的值,如果F>Fα(n,m-n-1),则拒绝原假设H0,接受备择假设H1,说明回归方程显著;如果F ③ 回归系数的显著性检验.本文是根据统计量t进行检验的,剔除对于自变量不起作用或者被其他解释变量代替对因变量起作用的解释变量.设原假设H0βj=0,备择假设H1βj≠0,i=1,2,…,n.,构建t统计量得 在指定显著水平α下,根据查统计学t分布表可知tα/2(n,m-n-1)的值,如果解释变量t≥tα/2(n,m-n-1),则拒绝假设H0βj=0,接受备择假设H1βj≠0,说明解释变量对被解释变量的影响是显著的;如果t 在建立回归模型之前,要对筛选的4个指标和GDP指标做相关性检验,通过相关系数来判断是否适合做多元线性回归.利用Python进行相关性分析,并可视化检验结果[12],如图3所示(见封3).从图中可知,相关系数都在0.9以上,说明经济指标GDP与指标之间存在高度的线性相关性,适合做多元回归分析. 将筛选的4个指标变量作为解释变量,经济指标GDP作为被解释变量,建立回归模型,得到模型汇总表,见表5;方差分析表,见表6;回归系数表,见表7. 表5 模型汇总Table 5 Model summary 表6 方差分析Table 6 Variance analysis 表7 回归系数Table 7 Regression coefficient 拟合优度检验.由表5可知,回归模型拟合指标R值为1.000,R2值为1.000,调整后的R2值为1.000,说明该回归模型拟合度较高,对于样本数据的解释度较高. F统计检验.本文设α=0.05,查统计学F分布表可知F0.05(4,9)=3.63,由表6可知,F的值为9 177.855,大于3.63且显著性P=0<0.005,说明回归方程显著,解释变量对被解释变量的线性影响显著. 由表7可知,常量的B值为-117 083.49,载货汽车总量X2的B值为86.415,港口吞吐量X8的B值为0.109,年末移动电话用户X10的B值为-0.160,交通邮政业增加值X11的B值为18.307,建立回归模型如下: t统计检验:设α=0.05,可知t(α/2,9)=2.262,该方程整体通过检验,但存在回归系数未通过检验的现象,如港口吞吐量t检验值为0.725,移动电话用户数t检验值的绝对值为0.266,都小于2.262,怀疑模型存在多重共线性.除此之外,根据方差膨胀因子法可知各个解释变量的VIF都是大于10,更加印证存在着较强的多重共线性,为消除存在的多重共线性,需要对模型进行优化. 本文将采取逐步回归的方式对回归模型进行优化,得到优化后的模型汇总表,见表8;方差分析表,见表9;回归系数表,见表10. 表8 优化后的模型汇总Table 8 Summary of optimized model 表9 优化后的方差分析Table 9 ANOVA after optimization 表10 优化后的回归系数Table 10 Optimized regression coefficient 拟合优度检验.由表8可知,模型拟合指标R值为1.000,R2值为1.000,调整后的R2值为1.000,说明优化后的模型拟合效果较好. F统计检验:设α=0.05,可知Fα(n,m-n-1)=F0.05(2,11)=3.982.由表9可知,F的值为19 999.89,大于3.982且显著性P=0<0.005,通过F统计检验.说明回归方程显著,解释变量对被解释变量的线性影响显著. 由表10可知,常量的B值为-111 960.289,交通邮政业增加值X11的B值为18.891,载货汽车总量X2的B值为105.459,建立优化后的回归模型如下: t统计检验:设α=0.05,可知t(α/2,11)=2.201.由表10可知,交通邮政业t检验值为35.688,大于2.201且显著性为0.000;载货汽车总量t检验值为11.339,大于2.201且显著性为0,上述自变量均通过回归系数检验,解释变量对因变量的影响是显著的. 综上所述,优化后的回归模型均已通过各项检验,说明以交通邮政业增加值和载货汽车总量为自变量建立的新回归模型拟合较优.说明优化后的回归模型可以用来预测我国GDP. 灰色系统是已知部分信息,未知部分信息的不确定性系统.灰色预测是对原始数据进行数据处理,通过掌握数据内在变动规律,生成有较强规律性的数据序列,然后构建对应的微分方程模型,进而科学准确地预测事物未来发展趋势[13]. 1) 初始化数据. 设X(0)为非负初始n个数据的序列,对其做一次累加(1-AGO)生成新的数据序列X(1),Z(1)为X(1)的邻均值等权生成序列. 其中, 即 其中,0≤α≤1,通常α=0.5. 2) 建立GM(1,1)灰色微分方程、白化微分方程. 将式(22)变形为 -az(1)(k)+b=x(0)(k),(k=2,3,…,n).(24) 其中a,b为待定模型参数. 3) 构建矩阵.将式(22)采用矩阵形式表达为 即 Xβ=Y(26) 其中, 5) 建立模型. 将求得的a,b带入式(23)求解该方程,得到GM(1,1)预测模型: 还原为原始序列,预测模型为 将式(28)带入式(29)得 6) 模型检验. 残差检验法进行精度计算检验,精度等级参照表,残差序列为 相对误差序列为 平均相对误差为 根据表1,本文将选取我国2012—2019年的交通邮政业增加值已知数据作为原始数列,来预测交通邮政业增加值.利用Python对原始数据序列进行处理分别得到一次累加序列X(1)和邻均值等权生成序列Z(1)如下: 在建立GM(1,1)模型之前,需要对原始数据序列进行级比检验: 利用Python建立矩阵X和Y: 通过Python分析得到,参数a=-0.084 741,b=22 915.252 1.据此可以得到GM(1,1)预测公式如下: 同理,本文也可以得到解释变量载货汽车总量的GM(1,1)预测公式如下: 求解出2012—2019年的交通邮政业增加值和载货汽车总量的预测值,计算出残差、相对误差以及平均相对误差[14],详见表11和表12. 表11 2012—2019年交通邮政业增加值的模型精度检验Table 11 Model accuracy test of the added value of the transportation and post industry from 2012 to 2019 表12 2012—2019年载货汽车总量的模型精度检验Table 12 Model accuracy test of the total number of trucks from 2012 to 2019 通过模型检验结果可知,交通邮政业增加值的GM(1,1)模型的平均相对误差为1.09%;载货汽车总量的GM(1,1)模型的平均相对误差为3.26%,模型的预测精度级别较高,可以用该模型对交通邮政业增加值和载货汽车总量进行预测,预测结果详见表13.再结合公式(15)完成对我国GDP预测,预测结果详见表14. 表13 交通邮政业增加值及载货汽车总量的预测值Table 13 The added value of the transportation and postal industry and the forecast value of the total number of trucks 表14 2020—2022年国内生产总值预测值Table 14 GDP forecast from 2020 to 2022 亿元 对交通邮政业增加值、载货汽车总量和国内生产总值GDP的原始数据和预测数据进行可视化,如图4所示.观察图4中交通邮政业增加值和GDP的观测值变化曲线,不难发现在2008年两者的增长速率同时降低,2009年一同回升,2011年再次同时降低,2016年再次一同回升,曲线变化规律基本相似;观察图4中载货汽车总量的观测值变化曲线,2006—2011年载货汽车增长速率呈现上升的趋势,GDP平均增长速率为11.032%,2012—2014年载货汽车增长速率降低,GDP增长速率为7.643%,2015年载货汽总量骤降,GDP增长速率为6.91%,较上一阶段减少了0.733%,2016—2019年载货汽车增长速率回升,GDP平均增长速率为6.54%,较上一阶段减少了0.37%,相对来说增加了0.363%.再根据式(15)可知,交通邮政业增加值和载货汽车拥有量的标准化系数均为正数,分别为18.891和105.459,说明载货汽车总量每增加1单位,将推动我国GDP提高105.459;交通邮政业增加值每增加1个单位,将推动我国GDP提高18.891. (a) 交通邮政业增加值变化曲线及预测(b) 载货汽车数量变化曲线及预测(c) GDP变化曲线及预测图4 交通邮政业增加值、载货汽车数量和GDP的变化曲线及预测Fig.4 Change curve and forecast of added value of transportation and post industry, number of trucks and GDP 综上分析,说明我国交通邮政业增加值和载货汽车总量对于我国GDP的增长具有一定的推动作用,从图4预测曲线也可以看出GDP在未来几年随着交通邮政业增加值和载货汽车总量增加而呈现逐渐上升的趋势. 通过构建指标体系、指标筛选和模型建立,最终确定交通邮政业增加值和载货汽车总量2个代表性物流指标来探究物流业对于我国经济的影响.根据预测结果可知,我国经济随着交通邮政业增加值和载货汽车总量持续增长,保持着稳固增长的态势,预计2022年我国GDP达到约127万亿元.交通邮政业增加值能够直接反映出对我国GDP的贡献,预计2022年交通邮政业增加值达到约5.57万亿元;载货汽车总量是物流业发展必不可少的环节,我国对载货汽车的需求日益增加,预计2022年载货汽车总量达到约3 193万辆.物流业对于我国经济发展有着重要的推动意义,我们亟需加快物流产业发展,推动智慧物流建设.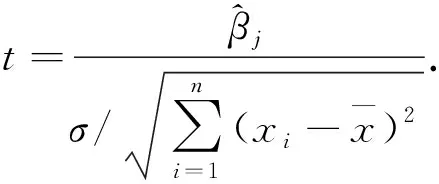
3.2 模型建立


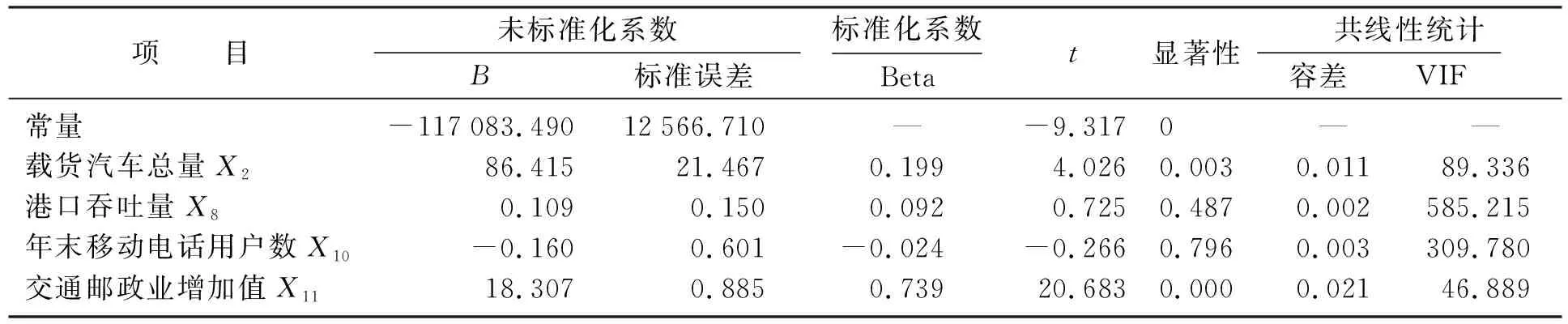
3.3 模型优化



4 GM(1,1)灰色预测模型
4.1 模型概述
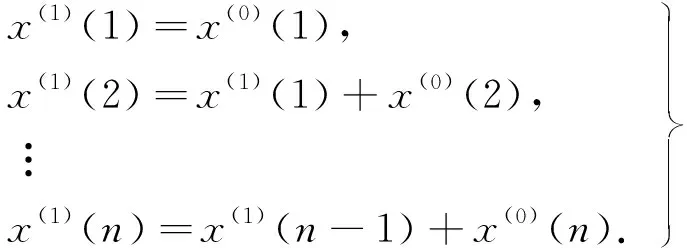
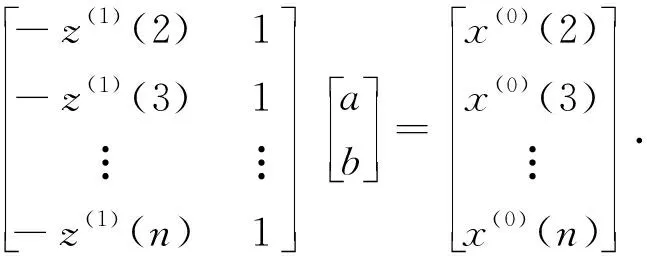
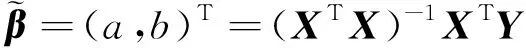
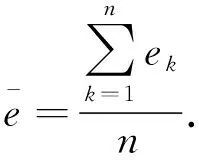
4.2 模型建立
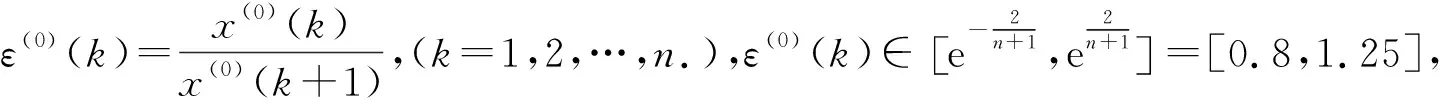

4.3 模型检验
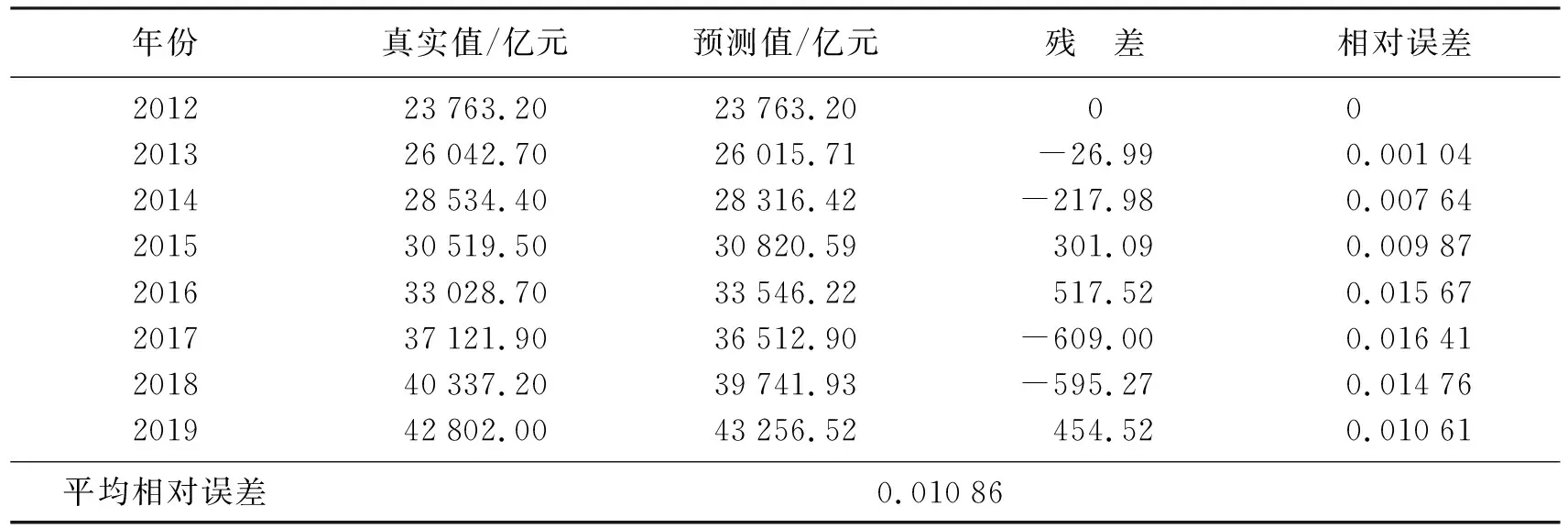
4.4 预测与分析

5 结 论

