基于蚁群算法的涡轮叶片外轮廓激光测量技术研究

朱思萌，王 健，闫晓燊，奚学程，赵万生

（上海交通大学机械与动力工程学院，机械系统与振动国家重点实验室，上海200240）

涡轮叶片是航空发动机的核心热端部件。现代航空发动机涡轮的入口温度超过了涡轮叶片的材料熔点温度，为防止叶片被融化，必须采用气膜冷却技术为叶片降温。涡轮叶片一般包含复杂的内腔和气膜冷却孔结构[1]，其结构强度主要由内腔筋板和耐高温的单晶体或定向晶体材料保证。为提高发动机的气动性能，叶片外轮廓被设计成复杂的自由曲面。涡轮叶片采用熔模铸造一次性精铸成形，铸造毛坯的单边余量最高可达0.05～0.1 mm[2]，若直接基于毛坯粗基准进行气膜冷却孔加工，会产生较大的加工误差，甚至造成废品。先进航空发动机涡轮叶片气膜冷却孔的加工精度要求可达±0.02 mm，而传统工艺方法主要依赖于人工经验，加工效率低、加工一致性难以保证，为满足自动化加工涡轮叶片气膜冷却孔的要求，需对涡轮叶片毛坯进行外轮廓测量，并根据轮廓偏差进行补偿，自适应计算加工程序。

涡轮叶片外轮廓的在线测量，除了要求较高的测量精度外，还要求测量速度满足生产节拍的要求，且由于涡轮叶片轮廓为自由曲面，测量过程中的轨迹规划也是难点之一。

目前涡轮叶片轮廓测量方法主要分为接触式测量和非接触式测量。涡轮叶片制造商广泛采用接触式三坐标测量仪进行铸造件抽检，该方法测量精度较高，但是测量速度慢，同时测量探针与工件易产生干涉碰撞。Chang等[3]开发了一种三坐标测量仪计算机辅助测量系统，可实现无碰撞测量路径规划。非接触式测量主要依赖深度相机、激光传感器等设备，通过光学扫描的方式提取表面数据，实现无碰撞的快速测量。Igarashi等[4-5]通过在曲面轮廓上激光投影特殊图案，依据图案的形变特征解析深度信息，实现曲面轮廓测量，该方法测量速度快、测量点数多，但是测量精度相对较低，难以满足涡轮叶片测量和生产要求。基于三角测量原理的激光位移传感器在非接触测量系统中较为常用，入射激光照射在工件表面形成光斑，再经由透镜投影到传感器，依据光斑在传感器中投影的位置计算出距离信息；但当激光束与待测点法向存在夹角时，会造成测量误差，称作物面倾角误差[6]。孙彬等[7]根据光能质心入射与接收的几何关系建立了物面倾角误差模型，测量误差随物面倾角的增大而增大，当入射激光与工件表面垂直时，测量精度最高。

切平面网格法采用平面逼近曲面的思路，激光器在切平面内沿网格逐点测量，一般适用于小曲率表面的简易测量，编程难度低、测量速度快，但测量精度相对较低。周欣康[8]采用等高截面法向测量法规划测量轨迹，在等高截面与涡轮叶片曲面的交线上选取待测点，入射激光在等高截面内与交线垂直，激光器沿叶片的等高截面环绕一周完成一个截面的测量，入射激光近似与工件表面垂直，测量精度较高；但由于每个截面的测量都需要传感器环绕一周，测量速度较低，同时待测点分布在若干截交线上，曲面整体特征的代表性较差。秦国辉等[9]基于OpenCASCADE平台，搭建了针对复杂曲面模型的自动检测系统，该系统采用Z字形轨迹遍历待测点，当曲面曲率较大时，需要往复调整姿态以实现法向测量，实际测量速度较慢。综上，现有涡轮叶片轮廓测量技术主要分为两类：一类是通过结构光学设备一次性地获取涡轮叶片完整轮廓，主要应用于三维重建，测量速度快、测量点云细密，但精度较低；另一类是通过搭载点测量传感器逐点测量，主要应用于实验室中对涡轮叶片铸造精度进行检测和分析，对测量速度没有太高要求，测量精度较高，但无法满足在线测量的生产节拍要求。

本文设计了一套涡轮叶片外轮廓在线自动测量系统。基于设计模型提取均匀分布的待测点，通过建立测量机床的运动学模型逐一求解各待测点的最佳测量姿态，并改进蚁群算法以优化各待测点的测量顺序，缩短测量时间。

1 测量点提取

为提升测量结果的代表性，测量点应该真实地贴合工件，并尽可能均匀地分布在待测表面。本文从CAD设计模型中提取待测点位，流程见图1。

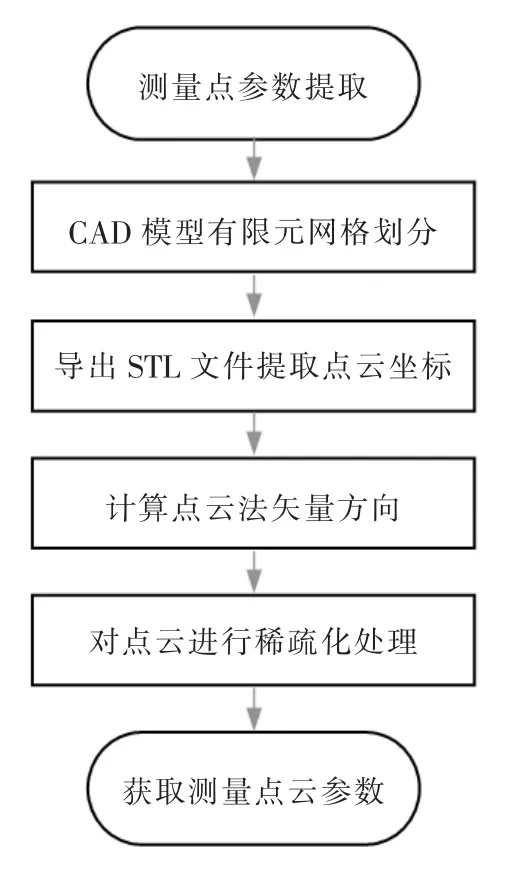
图1 测量点提取流程

图2是涡轮叶片的测量点提取过程。如图所示，将CAD设计模型转存为STL格式的文件后，即可获得一组轮廓表征点云，由于STL格式对实体表面采用三角剖分逼近曲面，只记录控制点之间的关系，因此在曲面弧度较大的位置控制点分布密集，弧度较小的位置控制点分布稀疏；通过对CAD设计模型进行三角网格划分，按照点云测量密度要求设定网格边长，可实现均匀密集轮廓点云的提取；从点云中剔除工件边缘、内部和被工装夹具遮挡住而无法测量的点，得到待测点云，并计算各待测点的法向矢量方向。

图2 涡轮叶片的测量点提取

2 法向测量姿态计算

激光测量时，入射激光投射在工件表面形成一个直径约为400μm的光斑，反射光线经过透镜到达接收器，根据反射角度和三角理论，可计算出激光器与工件表面间的距离。由于安装精度条件限制，无法实现激光位移传感器的测量光源方向与Z轴平行，即使通过标定校准也无法使测量光源与Z轴完全平行。根据图3所示的激光偏角误差示意，由于受激光入射光源偏角的影响，实际测量光斑不在激光起点的正下方，定义轮廓测量偏差为误差测量点与工件表面之间的距离。

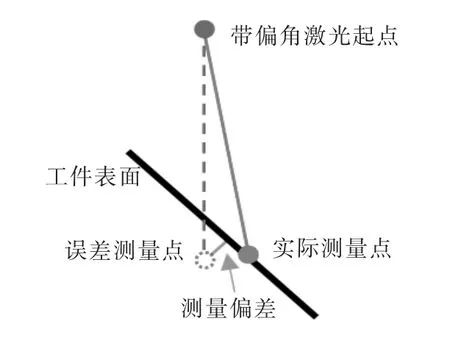
图3 激光偏角误差示意图

现假设测量光源与Z轴存在0.1°的夹角，激光光源与设定测量点的距离为50 mm，在工件表面不同倾斜角度状态下，获得的轮廓测量偏差见图4。可见，随着工件倾斜角度的增大，测量误差随之增大，入射激光与工件表面垂直时测量精度最高。

图5是本项目采用Z-Y-X-B-C构型测量机，激光位移传感器固定在Z轴执行器末端，工件及夹具固定在C轴平台上。根据机床构型，分别建立三个坐标系：机床坐标系OM、测量坐标系OL、工件坐标系OW。机床坐标系相对于机床固定，原点为BC轴交点，坐标系的xyz坐标轴与机床XYZ运动轴分别平行；测量坐标系固定在Z轴上，原点为Z轴执行器末端，坐标系的三个坐标轴与机床XYZ运动轴分别平行，当设定机床XYZ轴读数为（0，0，0）时，机床坐标系与测量坐标系原点重合；工件坐标系固定在C轴上，原点为BC轴交点，设定机床当BC轴读数为（0，0）时，机床坐标系与工件坐标系的XYZ坐标轴方向一致。

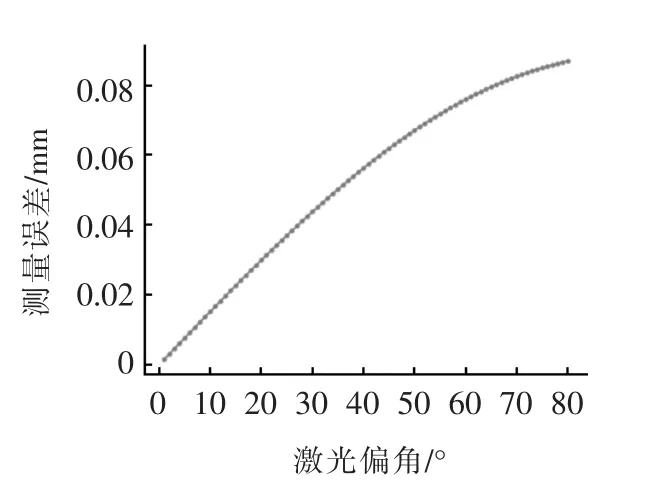
图4 激光偏角误差仿真

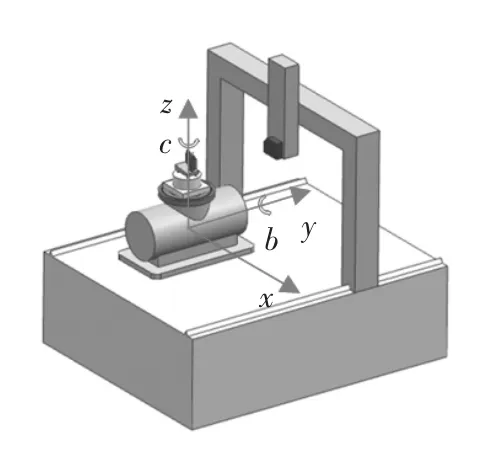
图5 测量机床结构示意图

设机床空间中一点Q，其在机床坐标系、工件坐标系、测量坐标系上的坐标分别为qM、qW、qL，则各坐标系间变换关系可以表示为：

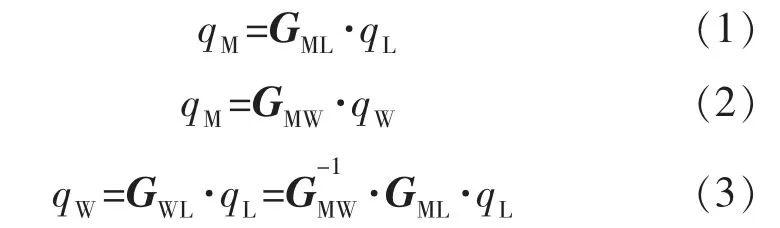
式中：GML为机床坐标系OM与测量坐标系OL的传递矩阵；GMW为机床坐标系OM与工件坐标系OW的传递矩阵；GWL为工件坐标系OW与测量坐标系OL的传递矩阵。

设机床各轴读数分别为（θx，θy，θz，θb，θc），则上述传递矩阵可分别表示为：

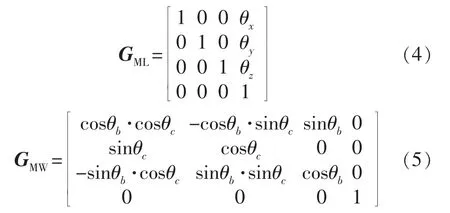
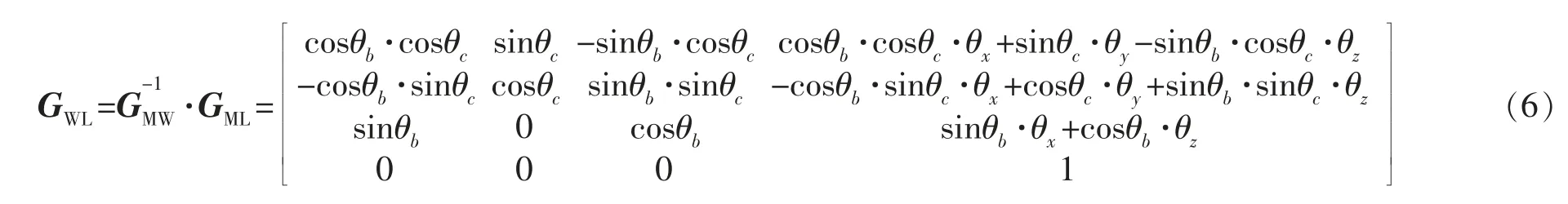
图6是机床的法向测量示意图，上侧为激光位移传感器测量示意，下侧为涡轮叶片待测点法向示意。设激光位移传感器的量程中点为P，则待测点在测量坐标系上的理想位置qL1=（0，0，-P），且qL2=（0，0，-P+1）为激光射线上距离qL1单位长度的点。

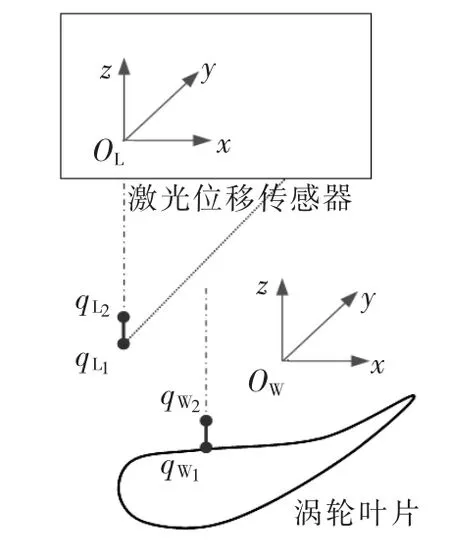
图6 法向测量示意图

基于设计模型得到待测点qW1=（x，y，z），待测点法线方向单位矢量为（nx，ny，nz），则qW2=（x+nx，y+ny，z+nz）为待测点法线方向上距离qW1单位长度的点。当激光位移传感器测量点向量与涡轮叶片待测点法向向量重合时，测量机处于理想测量姿态。分别代入式（3）中，即可构造关于传递矩阵GWL的方程组：

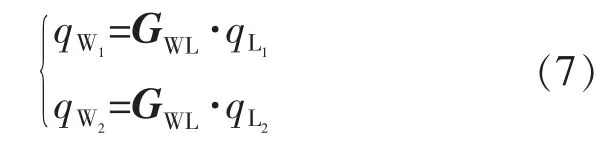
通过求解矩阵方程组（7），可得理想测量姿态下的测量程序。设机床各轴读数（θx，θy，θz，θb，θc），则GWL是（θx，θy，θz，θb，θc）组成的表达式：

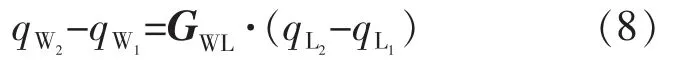
将式（6）代入方程，化简可得：

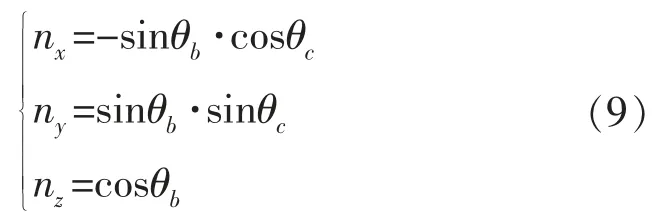
由于机械结构限制B轴的转动范围为[-90°，90°]，且左右转动对称，不妨设θb∈[0°，90°]；C轴转动无限制，设θc∈[0°，360°]，则可以求得θb和θc的唯一解。将式（6）和θb、θc范围代入方程（7）中，化简可得：

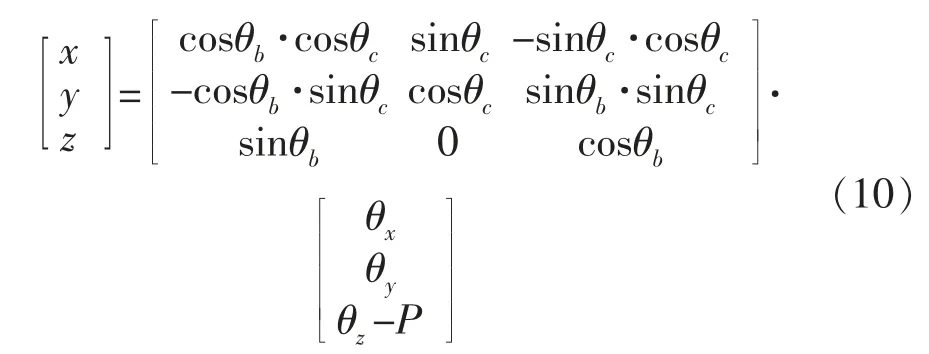
求解矩阵方程（10），可求得θx、θy、θz的唯一解。将（θx，θy，θz，θb，θc）代入其中，自动生成测量程序，即可实现待测点的法向测量。

3 蚁群算法的测量轨迹规划

完整的测量程序需要控制机床使激光位移传感器沿法线方向按照一定顺序遍历所有的待测点。由于单次测量时间相同，机床运动轴在相同进给倍率下运动速度相同，只有通过优化各待测点的测量顺序，减少机床在相邻两次测量间的运动时间，提高测量速度。因此涡轮叶片测量轨迹规划问题，可以抽象为通过优化待测点测量顺序达到测量时间最短的最优化问题，并且是一种在特殊机床运动空间下的旅行商问题。旅行商问题可以被描述为：给定若干个节点和两两节点之间的距离，求一条访问所有节点各一次的最短路线，属于多项式复杂程度的非确定性问题（NP问题）[10]。当节点数量较多时，在现有计算能力下，无法使用精确算法求解出路径规划的绝对最优解，一般采用蚁群算法、模拟退火算法、遗传算法、贪心算法等启发式算法求解。

Dorigo等[11]提出的蚁群算法，是一种用来寻找最优路径概率型算法。蚂蚁在不同节点出生，结合环境信息随机选择下一节点，记录走过的节点以防止重复和遗漏，更快完成遍历的蚂蚁在轨迹上留下的更多的信息素，以增加后续蚂蚁沿当前轨迹运动的概率权重，达到稳定状态后所有蚂蚁会沿着同一条最优轨迹完成所有节点的遍历。蚁群算法在工业领域常用于加工轨迹规划，张伟等[12]基于蚁群算法求解二维切割加工空行程规划问题，魏明强等[13]通过改进蚁群算法对PDC钻头刀翼上刀具安装孔的铣削加工轨迹进行优化，均显著缩短了运动行程，有效提高了加工效率。

本文通过运动学反解，将待测点最佳测量姿态映射到五个独立的运动轴，构造出具有实际意义的待测点间名义距离，并带入到蚁群算法中，求解各待测点的测量顺序，优化涡轮叶片测量时间。设两待测点在工件坐标系下的坐标分别为（x1，y1，z1）和（x2，y2，z2），则两待测点间的空间距离为：

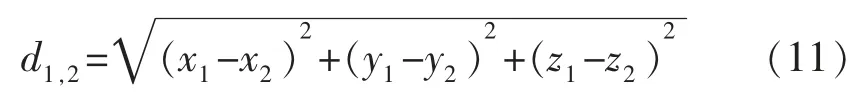
在法向测量程序中，根据式（9）和式（10）将实际两待测点之间的机床运动距离解析为各轴的独立运动距离。设两待测点的测量姿态分别为（θx1，θy1，θz1，θb1，θc1）和（θx2，θy2，θz2，θb2，θc2），则两待测点间的机床运动距离向量为：

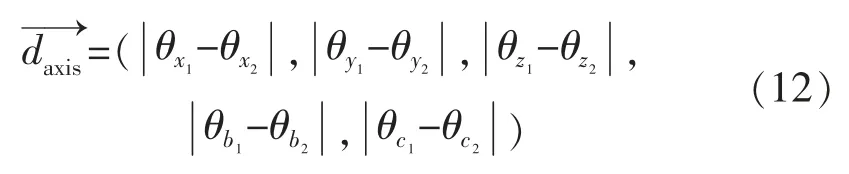
式中：XYZ轴为移动轴，mm；BC轴为旋转轴，单位为弧度；同时各轴的驱动速度存在差异，运动距离增量不能严谨地代表两待测点间的机床运动时间。

采用各轴独立驱动时的单位速度（vx，vy，vz，vb，vc）对机床运动距离向量进行归一化处理，得到两待测点间的机床运动时间向量：

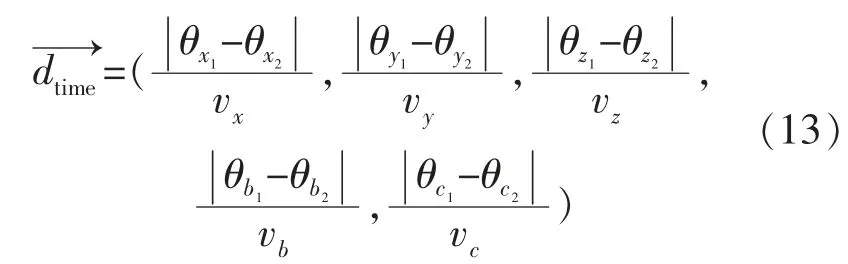
在相邻两次测量间，测量程序控制各轴独立运动，实现测量姿态的切换，耗时最长的运动轴决定了此次切换运动时间。因此两待测点之间的名义距离，即两待测点之间的机床实际运动时间，可以定义为：

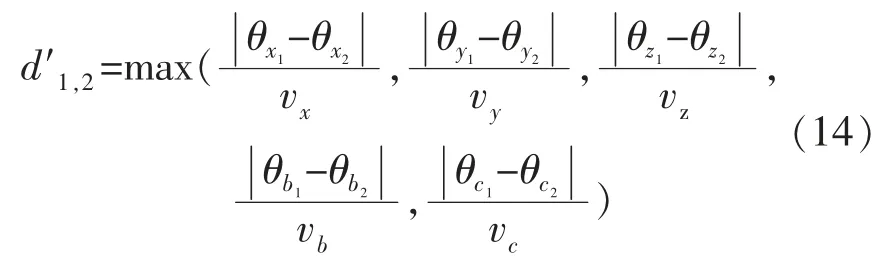
构造各相邻待测点间的名义距离矩阵：

假设n个待测点的遍历顺序为{r1，r2，r3，…，rn}，则相邻两次测量间的移动名义距离为d′ri，ri+1，则待测点遍历完成的总名义距离为：

使用式（15）中的名义距离矩阵作为蚁群算法的距离矩阵，总名义距离f为优化目标，进行启发式优化，得到的优化结果见图7，可见总名义距离f显著降低。

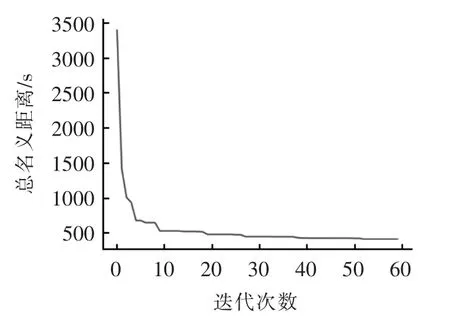
图7 测量轨迹优化过程

4 仿真验证

4.1 仿真模拟

以模拟导向叶片为待测零件，分别采用切平面网格测量法、等高截面法向测量法和蚁群算法法向测量法，分析和验证不同测量方法在测量精度和测量速度的差别。

切平面网格法测量轨迹规划方法，将待测量曲面按照法线方向划分为若干个部分。沿着每个部分的切平面方向建立轨迹平面，使得每个部分的测量角度相同。在同一轨迹平面内，激光传感器沿“之”字形网格进行测量，轨迹规划见图8。

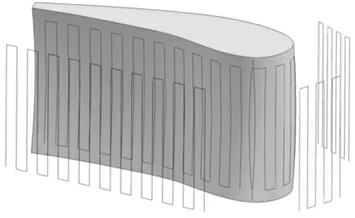
图8 切平面网格法测量轨迹规划

等高截面法向测量轨迹规划方法，沿工件的等高截面提取轮廓线，使待测点均匀分布在轮廓线上，并在等高截面内沿着曲线法线方向进行测量，轨迹规划见图9。

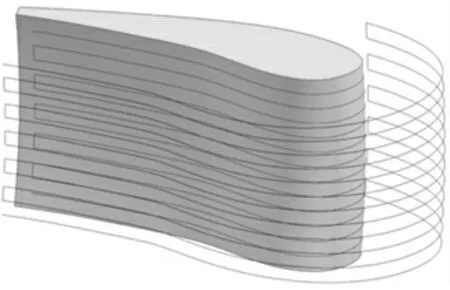
图9 等高截面法向测量法轨迹规划

蚁群算法规划法向测量方法，依据优化后的测量顺序，沿工件表面的垂直方向进行测量，使测量点均匀分布在工件待测曲面上，轨迹规划见图10。

4.2 仿真结果

仿真实验中，按照式（14）定义相邻两测量点间的机床运动时间，设定各轴独立运动速度，X轴20 mm/s、Y轴20 mm/s、Z轴20 mm/s、B轴3°/s、C轴3°/s，对各轴运动增量进行归一化处理，按照测量轨迹规划串联所有待测点得到测量时间T。根据图3所示的各待测点测量方向与法向之间的夹角，计算激光偏角误差，统计全部待测点的激光偏角误差，作为平均测量精度ε；然后分别采用切平面网格测量法、等高截面法向测量法和蚁群算法法向测量法设计测量轨迹，并统计测量点数、测量时间和平均测量精度，得到的仿真结果见表1。

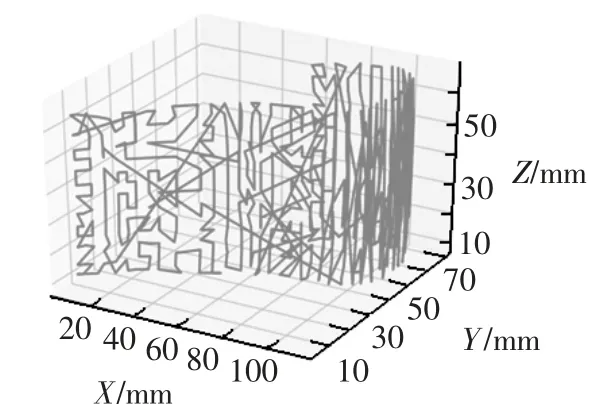
图10 蚁群算法法向测量轨迹规划

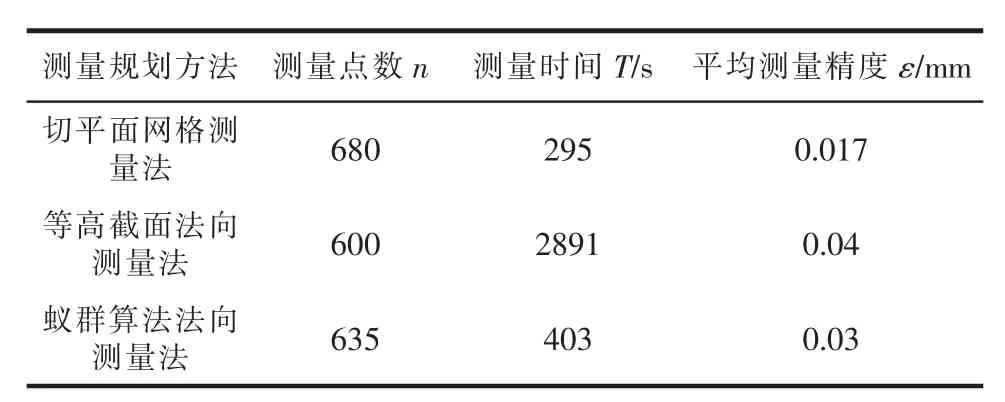
表1 各测量方法测量仿真结果对比

由仿真结果可得，切平面网格测量方法的测量速度最高，但是测量精度最低；等高截面法向测量法和蚁群算法法向测量法的测量精度都很高，且等高截面法向测量法的测量时间远大于蚁群算法法向测量法。然而，蚁群算法法向测量法，相较于切平面网格法平均测量误差由±17μm下降到±3μm，相较于等高截面法向测量法平均测量时间缩短86.8%，具有重要的实际意义。

5 结束语

针对航空发动机涡轮叶片轮廓测量精度差、速度慢的问题，本文设计一套涡轮叶片外轮廓自动测量系统。首先，针对涡轮叶片外轮廓形面特征，通过网格化曲面分割和点云采样，提取到分布均匀、更具代表性的待测点集合；其次，针对五轴激光测量机床结构，通过旋量理论建模和运动学反解，计算出各待测点的最佳法向测量姿态；最后，针对大批量无序待测点的轨迹规划，提出一种适用于特殊机床空间下蚁群算法规划的名义距离，通过蚁群算法规划自动生成五轴激光测量机测量程序。通过与切平面网格法和等高截面法向测量法的仿真实验对比表明，所提出的蚁群算法规划相较于切平面网格法平均测量误差由±17μm下降到±3μm，相较于等高截面法向测量法平均测量时间缩短86.8%，能够快速准确的进行涡轮叶片外轮廓测量。