扭转振动数值分析的粘弹性传输边界
付 浩,仝 睿,宋二祥
(清华大学土木工程系土木工程安全与耐久教育部重点实验室,北京 100084)
有限元数值模拟方法是解决土动力问题的重要手段。采用有限元方法进行动力问题计算,一般只能选取有限范围的计算网格,同时在网格的人为截断边界处设定特殊的传输边界,以实现对真实无限域上波动的模拟。近年来,国内外对人工传输边界问题已有了广泛的研究,文献[1−2]分别对各类传输边界的成果与进展进行了综述。
Lysmer 和Kuhlemeyer[3]最先提出的粘性边界通过对一维平面波的分析导出,其做法是在人为截断边界上布设阻尼器。因其概念清晰,应用方便,而被广泛采用。但粘性边界存在一定缺陷:一方面,粘性边界的推导中未考虑波的振动幅值随波的扩散发生几何衰减;另一方面,粘性边界处不能考虑外部介质的静刚度,这就使其存在低频稳定性问题。
Deeks 和Randolph[4]通过分析水平传播的柱面波给出径向及竖向波动分析的粘弹性传输边界,相应边界条件是在边界上布设阻尼器的同时,也布设弹簧。相比于粘性边界,粘弹性边界能模拟人工边界外介质的弹性恢复性能,具有良好的高频和低频稳定性。刘晶波等[5]对Deeks 和Randolph提出的人工边界进一步发展完善,并通过对球面波的分析提出三维粘弹性边界。
但Deeks 和Randolph 没有给出针对质点在柱面环向振动波,亦即SH 波的传输边界条件。而这种边界条件对动力机器基础扭转振动以及地震作用下不规则建筑发生的扭转振动进行分析时是需要的。实际上,此类扭转振动在分层地基中引起的Love 波正是以竖直圆柱面为波阵面沿水平方向向外传播的。
刘光磊、宋二祥[6]将Deeks 和Randolph 针对单相介质的人工边界拓展到饱和多孔两相介质,建立了饱和两相介质时域动力固结分析的粘弹性人工边界,计算表明其总体效果较好。但其中针对SH 波的人工边界条件,针对微分方程近似解的假设偏于简化,尚有进一步优化的空间。
Du 和Zhao[7]基于无限域动力刚度有理近似的连分式展开技术, 建立了针对一般弹性介质的高阶时域粘弹性传输边界。Zhao 等[8]建立了针对多层介质的高阶时域粘弹性传输边界。Li 和Song[9]则针对饱和多孔两相介质建立了高阶时域粘弹性传输边界,并通过数值模拟验证了此类边界的计算精度。但对一般弹性介质中SH 波分析的粘弹性边界的深入讨论还鲜见报道。
本文假设波动以柱面波的形式传播,推导针对一般弹性介质中SH 波进行数值分析的粘弹性传输边界。由于采用近似解,依推导过程的不同,给出两种不同的人工边界,并对这两种人工边界的合理有效性进行理论分析和数值模拟验证。由于在弹性假设下,剪切波并不会引起超静孔压,因此本文的边界既适用于单相体,也可推广到饱和土地基等两相体中。将此人工边界条件与已有针对P 波、SV 波的人工边界条件结合可以实现三维波动问题的有限元分析。
1 柱面波平面内剪切粘弹性传输边界构造
假设波动以柱面波的形式传播,采取如图1所示无限大单位厚度圆盘进行分析。选用柱坐标系,坐标轴分别为r、θ、z,并记各方向的位移分别为ur、uθ、uz。震源位于圆盘中心。

图1 轴对称无限平面圆盘Fig.1 Axisymmetric infinite plane disk
柱面波可解耦为P 波、SH 波和SV 波三类波,分别对应上述圆盘平面内径向、平面内剪切和平面外剪切振动的运动形式[10]。对于P 波和SV波,Deeks 和Randolph 已给出了在边界处位移与应力的关系式,并构造了合理有效的粘弹性传输边界,分别如式(1)、式(2):

以下采用两种略有不同的两种推导方法,分别给出圆盘平面内剪切波动分析的两种粘弹性传输边界。
1.1 粘弹性传输边界一
按给定柱坐标系,设震源在 θ向振动,振动将以SH 波的形式向四周传播。在柱坐标系中,列出振动的平衡方程、物理方程及几何方程如式(3)。由于振动具有绕轴中心对称的性质,因此各物理量对 θ的导数为0。
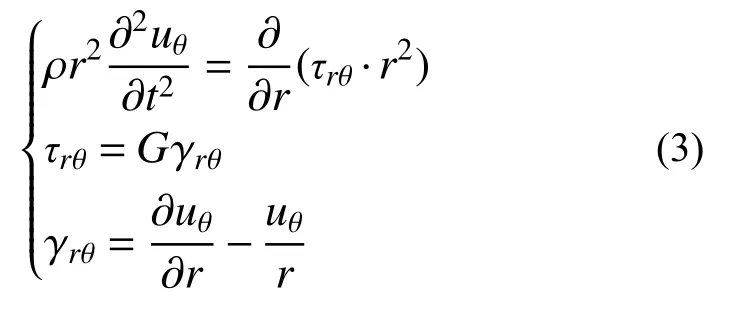
式中,τrθ为圆盘平面内切向的剪应力。
由此可得到SH 波的波动方程:

为求解以上方程,引入如式(5)定义的位移势函数 ϕ:


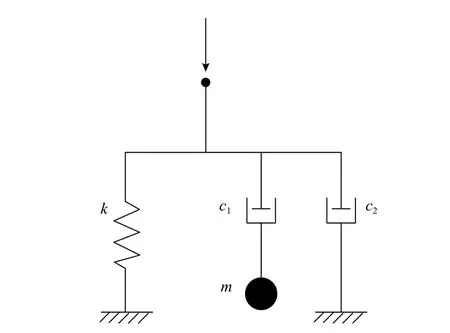
图2 第一种粘弹性传输边界模型Fig.2 The first viscoelastic transport boundary model
1.2 粘弹性传输边界二
除了前文提到的推导方法外,使用另一种转化方法,可以得到不同的粘弹性传输边界。注意到:

注意到此时边界处的剪切应力与切向位移的关系与Deeks 和Randolph 文章中平面内法向的边界条件表达式接近,故可采用如图3 所示的元件模型以模拟该边界条件,选取适当的元件参数,与元件系统相连的边界微元面的应力与位移可满足式(17)的关系。对于距震源R处的平面内切向边界,其单位面积上模拟远场介质作用的等效物理元件的力学参数分别为k=2G/R,c=ρVS,m=2ρR。
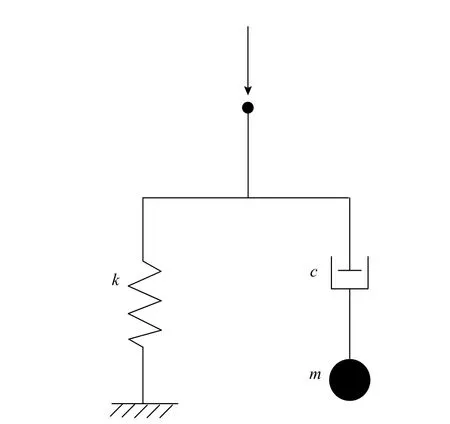
图3 第二种粘弹性传输边界模型Fig.3 The second viscoelastic transport boundary model

1.3 上列两人工边界的合理性论证
以上对同一问题的分析得出两种不同的人工边界条件。那么哪一种更为合理呢?本节试图回答此问题。这里提出的一个观点是,当振动频率很低时,人工边界条件应退化为静力边界条件,也就是人工边界的刚度应等于静力刚度。符合此要求的人工边界条件,至少其低频精度较好。
由于一般弹性力学教科书中没有给出此问题的静刚度,这里给出相应的推导。选取有孔圆盘,内径为r0,圆盘在孔内侧受平面内切应力q0。由微元体的平衡方程可得到:

式中,C1、C2为与边界条件有关的待定系数。
考虑无限大有孔圆盘,其边界条件为:

与前面给出的粘弹性边界条件对比可见,第二种传输边界其弹簧刚度与静刚度相等,其低频精度会较好,在理论上也应该更为精确。随后的数值模拟计算也验证了这一推断。
事实上,第二种传输边界同样通过势函数的近似解推出,但却得到了与第一种传输边界不同的结果。这是由于式(7)并非势函数的精确解,随后利用此近似解进行推导的不同代入过程即会得到不同的结果。从数学的角度来说,二者均为近似解,但第二种方法恰可以满足静刚度的要求,且具有更精简的表达式与元件模型。
2 数值计算验证
2.1 模型及参数
这里使用COMSOL 计算软件对无限体中的柱面波进行模拟,以验证上述两种粘弹性传输边界的有效性,并分析其精度。算例考虑二维轴对称平面应变问题,使用圆环网格,内径为10 m,外径为50 m。计算模型如图4 所示。
材料参数参考中硬砂土层选取,G=79.6 MPa,材料密度ρ=2650 kg/m3,由此可知波速V=173 m/s。
对人为截断边界分别设为粘弹性传输边界一、粘弹性传输边界二和固定边界进行对比分析。在内边界分别施加如图5 所示两种扭矩荷载。计算时长为1 s。同时还给出网格足够大(外径500 m),计算时间内反应不受边界影响的结果作为真实解的参考值,这与文献[12−13]中参考解的处理方法一致。

图4 模型网格示意图Fig.4 Model grid diagram
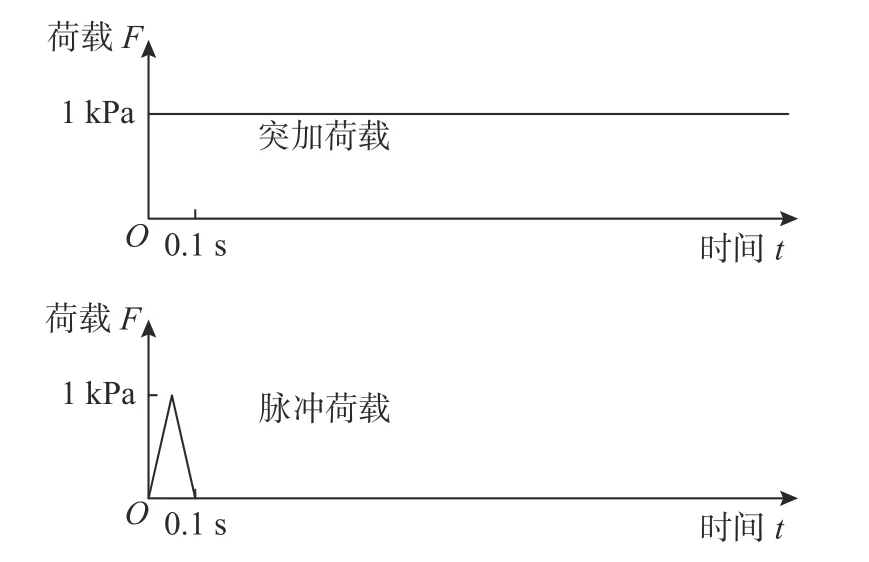
图5 荷载示意图Fig.5 Load diagram
选取模型内径处(r=10 m)、A点(r=20 m)和B点(r=40 m)处数据进行分析。
2.2 突加荷载下的计算结果分析
图6 为模型在突加荷载作用下,模型内径处(r=10 m)的环向位移计算结果。将位移值除以F0R/G,进行无量纲化处理。其中,F0为荷载峰值,R为模型外边径,此处为50 m。比较了固定边界与本文提到的两种传输边界同参考解之间的差别。结果表明,在突加荷载作用下,模型内径处变形量不断发展。在反射波回传之前,固定边界模型的变形量相差不大。但是当反射波传回之后,固定边界模型与参考解之间可以看到明显的差别。而两类传输边界模型都和参考解较为接近,且第二种传输边界模型更为精确。
图7 和图8 显示了在突加荷载作用下,三种模型中A点和B点的位移大小及其与参考解的比较。可以看出,距荷载点越远,固定边界与参考解之间的偏差会越大。同时固定边界偏差开始明显的时间点会受到反射波到达时间的影响。而两种传输边界条件依然可以较好地反映外部土作用,得到的结果和参考解较为接近。第二种传输边界模型同样更为精确。

图6 突加荷载下内径处环向位移Fig.6 Circular displacement at inner diameter under sudden load

图7 突加荷载下A 点环向位移Fig.7 Circular displacement of point A under sudden load
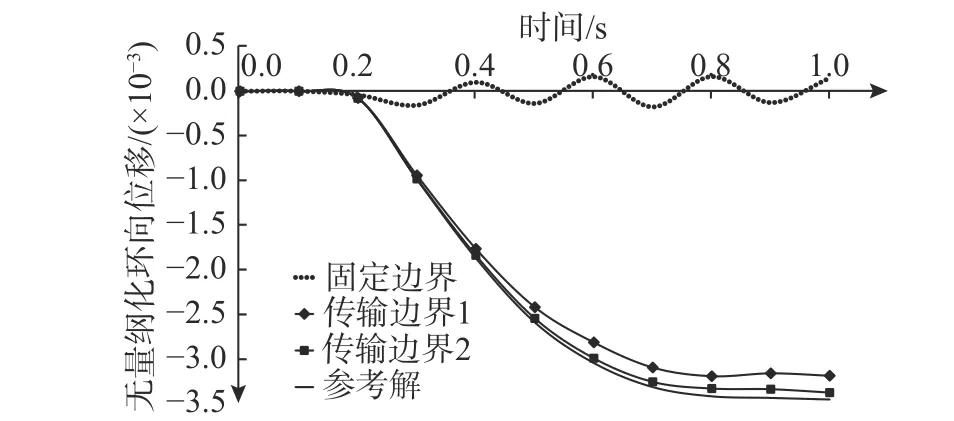
图8 突加荷载下B 点环向位移Fig.8 Circular displacement of point B under sudden load
2.3 脉冲荷载下的结果分析
图9 和图10 给出了冲击荷载作用下A点和B点的环向位移计算结果。在冲击荷载作用下,位移量更小,固定边界模型会出现明显的震荡情况,而两种传输边界则可以较好地模拟实际情况。同样,第二种传输边界得到的结果会更为精确。

图9 冲击荷载下A 点环向位移Fig.9 Circular displacement of point A under impact load

图10 冲击荷载下B 点环向位移Fig.10 Circular displacement of point B under impact load
3 结论
本文通过分析水平传播的柱面波,推导给出了针对一般弹性无限介质内SH 波传播问题数值分析的粘弹性边界,对所给人工边界的合理有效性进行了理论分析和数值模拟检验。由于在推导过程采用相应微分方程的近似解,不同的推导过程可给出不同的人工边界条件,两种人工边界的计算结果均可达到满意的精度,但满足静力刚度条件的第二种传输边界精度更高。尽管本文只分析了单相体的情况,但由于在弹性假设下,剪切波并不会引起超静孔压,因此本文的边界既适用于单相体,也可推广到饱和土地基等两相体中。

