环氧沥青铺装对钢桥面板受力影响试验研究

王石磊，齐法琳，柯在田，高 岩

(中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081)

正交异性钢桥面板(以下简称“钢桥面板”)具有自重轻、整体刚度大、施工速度快的特点，是大跨度桥梁最常使用的桥面形式[1]。为确保车辆行驶的舒适性和减少车行荷载对钢桥面的冲击，通常在钢桥面板上设置铺装层，我国钢桥面板常用铺装形式有改性沥青SMA、浇注式沥青混凝土和环氧沥青混凝土三种方案[2]。随着钢桥面板的广泛使用和服役时间的逐渐增加，该类结构产生了不同程度的疲劳裂纹[3]。研究表明改进铺装层结构或确保铺装的完整性，可以减小钢桥面板关键部位的受力，进而延缓钢桥面板疲劳敏感部位的使用寿命[4−7]。

国内某悬索桥钢箱梁竣工时桥面铺装采用改性沥青SMA 方案，通车运行数年后原有铺装频繁出现推移、车辙、开裂的现象，钢桥面板U 肋与面板连接部位、U 肋与横隔板连接部位、U 肋嵌补段出现了大量的疲劳裂纹，管养部门针对钢桥面板疲劳开裂开展了专项的维修加固处理，同时将原铺装更换为强度高、耐腐蚀性及疲劳性能好的环氧沥青混凝土铺装[8]。为考察环氧铺装对钢桥面板关键部位受力改善效果及稳定性能，笔者开展了长达6 年的实桥试验研究，以期为同类工程应用及钢桥面板病害处治提供参考和借鉴。

1 背景桥梁概况

1.1 钢桥面板结构简介

本文背景桥梁为悬索桥，加劲主梁采用扁平闭合流线型钢箱梁，桥面宽度为35.6 m，按双向六车道设计，吊索纵向间距12 m，桥面系采用钢桥面板结构，桥面板厚12 mm，闭口U 肋规格为320 mm×260 mm ×8 mm，横向间距620 mm。横隔板板厚8 mm，纵桥向间距4 m。钢桥面板细部构造如图1 所示。

1.2 钢桥面板病害

背景桥梁钢桥面板主要存在以下4 种类型病害，分布示意如图2 所示。

1) 部位1：U 肋与面板连接焊缝位置处裂纹，裂纹竖向贯穿面板；

2) 部位2：U 肋与横隔板连接部位弧形切口处裂纹，裂纹沿横隔板母材斜向发展；

3) 部位3：U 肋与横隔板连接竖向焊缝下端部裂纹，裂纹沿横隔板母材斜向发展；

4) 部位4：U 肋嵌补段现场焊缝位置处裂纹。

图1 钢桥面板细部构造 /mm Fig.1 Configuration of steel orthotropic deck

图2 背景桥梁钢桥面板病害分布Fig.2 Fatigue crack layout of orthotropic steel deck

1.3 环氧沥青混凝土铺装

铺装设计厚度70 mm，结构组成为：35 mm环氧沥青混凝土(EA10)+粘结层+35 mm 环氧沥青混凝土(EA10)+防水粘结层，结构如图3 所示。

图3 环氧沥青混凝土铺装方案Fig.3 Structure of epoxy asphalt concrete pavement

2 试验方案

为分析环氧沥青混凝土铺装对钢桥面板局部应力和变形的改善效果，在不同铺装状态(原铺装、铺装铲除后、新铺装)及不同环境(低温、高温)下开展现场试验，并基于新铺装的材料特征建立了有限元仿真计算模型，对比实测与理论计算结果，研究测试部位受力特点和规律。

2.1 有限元仿真模型

有限元模型忽略第一体系的影响，模型横桥向宽6200 mm，包含10 道U 肋，为横向测试区域的5 倍，纵桥向长16000 mm，覆盖4 道横肋间距，为纵向测试区域8 倍，测试区域、模型计算区域、半幅钢箱梁断面布置如图4 所示。采用ABAQUS建立钢桥面板计算模型，单元采用C3D8R 型8 节点缩减积分实体单元，对试验重点关注部位进行了单元细分，网格尺寸按应变计敏感栅长进行控制，部位1 单元尺寸约为2 mm，部位2 单元、3 单元尺寸约为3 mm，部位4 单元尺寸约为5 mm。模型边界条件按四边简支考虑，约束桥面板及横肋四周对应节点的x、y、z方向位移。桥面铺装与钢板间采用界面耦合进行约束，不考虑材料非线性及界面滑移的影响。有限元模型如图5 所示。环氧沥青混凝土弹性模量与温度相关，结合背景桥梁当地平均温度，确定铺装层的弹性模量为3000 MPa，泊松比为0.25[9−10]；钢材弹性模量为210 GPa，泊松比为0.3。

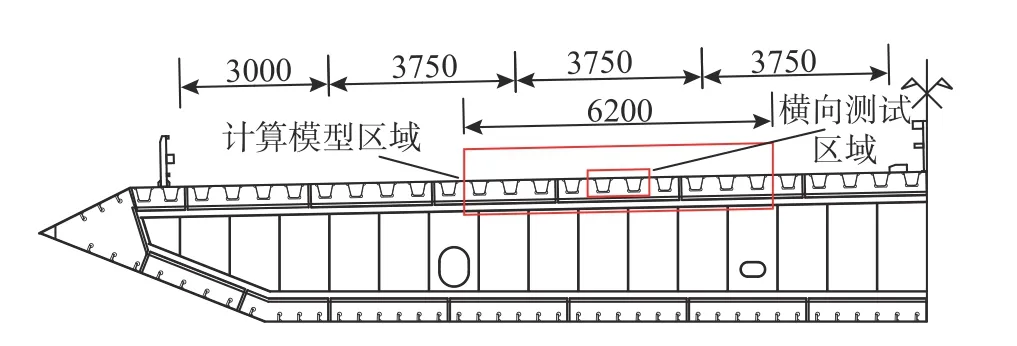
图4 测试及计算区域横桥向布置 /mm Fig.4 Transverse layout of test and calculation area

图5 有限元模型Fig.5 Finite element model

2.2 测点布置

背景桥梁钢桥面板4 种类型病害空间分布零散，测试区域选择前进行了现场调查，保证测试区域前后2 道横肋及横向6 道U 肋(1 个车道)范围内均未出现疲劳裂纹，以避免病害影响测试结果、有利于实测与有限元计算结果比较。

试验选择纵肋与面板连接部位、纵肋与横隔板连接部位进行局部应力测试，纵向设置了A-A、B-B、C-C 三道测试断面。A-A 测试断面兼做钢桥面板变形测试断面。测点布局如图6 所示。

图6 试验测点布局 /mm Fig.6 Distribution of testing points

钢结构应力选用中航电测电阻应变计测量，其中U 肋嵌补段纵向应力选用敏感栅长5 mm 的BE120-5AA 型单向应变计，横隔板处局部应力选用45°夹角敏感栅长3 mm 的BE120-3CA 型三向应变计，U 肋与面板连接部位局部应力参考热点应力法[11]选用敏感栅长2 mm 的BE120-2GD 型双组应变计。每次试验前均对各应变计防护及绝缘状况进行检查，确保测试结果的可靠，图6 中所示测点为经验证和分析在6 年周期内均稳定的测点，其他过程中受到破坏或绝缘状况不佳的测点未含在本文之列。钢桥面板变形采用千分表测量。部分测点安装状况如图7 所示。

2.3 试验加载

图7 测点现状安装状况Fig.7 Installation condition of measuring points

试验加载采用双轴货车，加载重量充分考虑超载车辆的影响，前轴重为90 kN，后轴重320 kN(加载轮)。加载车轴距及车轮触地面积布局如图8(a)所示，基于影响面的思路进行计算和加载，横桥向设置37 条加载线，如图8(b)之T1～T37，纵桥向设置15 个加载轮位，如图8(c)之L1～L15，受试验时间限制，结合加载位置与测试部位的关系，选取典型计算工况进行实桥加载。现场试验组织状况如图9 所示。

图8 试验加载控制 /mm Fig.8 Loading procedures

图9 现场试验照片Fig.9 Field test photos

2.4 试验工况

实桥试验共计进行了7 次，时间跨度为6 年。试验工况安排见表1。

表1 试验工况安排Table 1 Arrangement of field test

为减少环境对试验结果的影响，试验均在凌晨0:00～3:00 时间段及交通封闭条件下开展。历次试验确保测点位置、加载车辆及点位的统一。试验数据按实际车辆后轴重与计算轴重320 kN 的比值进行线性换算后再进行对比分析。

3 试验分析

3.1 U 肋与面板连接部位受力分析

图10 M1、M2 测点推算焊趾处应力结果Fig.10 Calculated stress of weld toe by M1&M2

U 肋与面板连接部位(部位1)典型测点应力与横向加载线的关系如图10 所示，试验加载轮位作用下应力实测与理论计算变化规律一致，试验荷载控制轮中心位于测试部位正上方时应力达到峰值，测试部位受加载线横向位置影响较大，横向影响区域约为2 道U 肋中心距(640 mm)，由于控制轮双胎影响，同一横向影响区内，应力存在双峰的现象，因考虑了左、右侧轮同时加载，未试验加载的计算轮位与试验轮位作用下的应力变化规律存在重演现象。相对于无铺装状态，铺装对测试部位应力均存在改善，新铺装状态下测试部位受力与温度有强关联性。

3.2 U 肋与横隔板连接处受力分析

对平面应力状态下的45°应变花测点，按照式(1)算出最大主应力、剪应力[12]。

式中：E为钢材弹性模量；σ1为主拉应力；σ2为主压应力；τmax为剪应力；µ为钢材泊松比；ε0、ε45、ε90为三向应变测试结果。

横隔板弧形切口处(部位2)及横隔板与U 肋连接竖向焊缝下端(部位3)典型测点主拉应力与横向加载线关系如图11 所示。当荷载沿测试横肋横桥向移动时，计算及实测结果均表明当试验荷载控制轮中心作用于测试部位正上方时该部位主拉应力较小，远离该部位一个纵肋间距后主拉应力达到峰值，主拉应力实测与理论计算变化规律相近，计算主拉应力横向影响范围为2 道U 肋间距(1240 mm)，存在不同的是理论计算的主拉应力横向梯度更大，即主拉应力实测横向影响范围大于理论计算结果，实际结构受力更为不利，因单元网格尺寸已按照应变计敏感栅长进行精细化设置，网格划分影响可以忽略，实测与理论计算的偏差体现了钢桥面板连接部位局部受力行为的复杂性和仿真计算的有限性。

部位2 及部位3 典型测点主拉应力与纵向加载轮位关系如图12 所示。当荷载沿纵桥向移动时，计算及实测结果均表明当试验荷载控制轮中心作用于测试部位对应横肋时主拉应力达到峰值，说明测试部位以承受横隔板面内受力为主，主拉应力实测与理论计算变化规律一致，计算测试部位主拉应力纵向影响范围为2 道横肋间距(8000 mm)。

图11 典型测点主拉应力与横向加载位置关系Fig.11 Principal tensile stress with transverse loading line

相对无铺装状态，铺装对测试部位应力均存在一定改善，新铺装状态下，测试部位受力与高低温环境有弱关联性。

图12 典型测点主拉应力与纵向加载轮位关系Fig.12 Principal tensile stress with longitudinal loading wheel position

3.3 U 肋嵌补段受力分析

U 肋嵌补段(部位4)典型测点应力与横向加载线的关系如图13 所示。试验加载轮位作用下测试部位应力实测与理论计算变化规律一致，应力横向影响区域约为4 道U 肋间距(2480 mm)。当试验荷载控制轮中心位于测点所处的纵肋顶部时受力最为不利，因考虑了左、右侧轮同时加载，未试验加载的计算轮位与试验轮位作用下的应力变化规律存在重演现象，因应力横向影响区域大于车宽，左、右轮作用存在叠合区间。相对无铺装状态，铺装对测试部位应力均存在改善，新铺装状态下，测试部位受力与高低温环境有强关联性。

3.4 钢桥面板变形分析

钢桥面板典型测点(D3)挠度与横向加载线的关系如图14 所示。试验加载轮位作用下测试部位应力实测与理论计算变化规律一致，挠度横向影响区域约为4 道U 肋间距(2480 mm)。当控制轮中心位于面板测点临近U 肋腹板顶部时面板变形达到峰值，受加载轮双胎净距的影响，当控制轮中心位于面板测点顶部时面板变形有所回落。因考虑了左、右侧轮同时加载，未试验加载的计算轮位与试验轮位作用下的变形变化规律存在重演现象，因变形横向影响区域大于车宽，左、右轮作用存在叠合区间。结果表明相对无铺装状态，铺装对测试部位变形均存在一定改善，面板变形与高低温环境有强关联性。

图13 L1、L2 测点平均应力测试结果Fig.13 Average stresses of L1 and L2

图14 典型测点挠度测试结果Fig.14 Measured deflection at typical measuring points

3.5 结果对比分析

对比实测与理论计算结果可知，最不利试验荷载作用下理论计算结果与新铺装完成时(新-11-01)实测结果相近，具体分布见表2。

不同测试部位历次试验不利值见表3，相对无铺装状态不同试验条件下钢桥面板受力及变形改善效果见表4。

表2 实测与理论计算结果对比Table 2 Measured and theoretical calculation results

表3 不同测试部位历次试验不利值统计Table 3 Statistics of critical measurements of corresponding regions

表4 应力及变形改善效果Table 4 Stress and deflection improvement effects

1) 从应力值看，钢桥面板4 个疲劳敏感区域在试验荷载作用下承受较大的应力，原铺装状态下测试部位应力绝对值为119 MPa～136 MPa，铺装铲除后为125 MPa～179 MPa，新铺装高温环境下为113 MPa～133 MPa。

2) 从新铺装改善效果看，在低温环境下，铺装运营6 年后，疲劳敏感部位1～4 应力改善效果分别为80%、14%、32%、46%，面板变形改善27%，U 肋变形改善31%，新铺装改善效果优于相近环境下原有铺装的改善效果。

3) 4 个疲劳敏感部位实测应力随环境温度的变化关系如图15 所示，各部位应力与环境温度存在线性关联，随温度变化的速率k值差异较大(k1=−4.00，k2=0.64，k3=1.89，k4=1.91)。疲劳敏感部位应力与温度线性关联的特点与文献[13−14]基于钢桥面板的监测结果所揭露的现象一致。

图15 疲劳敏感部位实测应力与温度关系Fig.15 Stress of sensitive regions of fatigue crack with temperature

4 考虑温度的疲劳寿命改善效果分析

4.1 桥梁整体温度环境

为考察背景桥梁所处自然温度环境，从当地气象部门获取了一整年365 d 的实测结果作为分析样本，数据来源于桥址附近3 km 气象部门布设的观测站记录。一年期整点温度时程如图16 所示。

图16 一年整点温度记录Fig.16 Hourly temperature record of one whole year

由4 个疲劳敏感部位实测应力与温度存在线性关联，为修正温度对应力的影响，特将历次测试结果修正至年均温度。为获取某时间区段内平均温度，采用复化梯形求积公式(2)[15]求得温度沿时程的积分。

式中：Tn为积分值；n为积分点数目，可按逐月或逐年取值；hk为积分步长，取为1h；f(xk)为k时刻温度值；f(xk+1)为k+1 时刻温度值，平均温度为Tn除以n。按照本方法求得年均温度为23.7 ℃。

4.2 疲劳寿命改善效果分析方法

国内外规范中桥梁钢结构抗疲劳设计均是着眼于细节构造，对易发生疲劳破坏的细节构造进行分类疲劳评定，不同细节构造类别对应不同的Δσ-N曲线[16]。Δσ-N曲线方程式一般在双对标坐标中表示，如下式：

式中：N为对应Δσ 作用下的疲劳循环次数，即疲劳寿命；Δσ/MPa 为外加应力幅；A为曲线的截距；m为曲线斜率，日本规范中取值为3，中国及欧洲规范分段考虑，分别为3 和5，如图17 所示[1]；C为循环次数的统计偏差。

图17 细节构造Δσ-N 曲线特点Fig.17 Typical Δσ-N curve for a fatigue vulnerable location

式(4)和式(5)分别为某评定部位在应力幅Δσ1及应力幅Δσ2作用下其疲劳寿命N1及N2的求解公式，将式(4)减去式(5)可得：

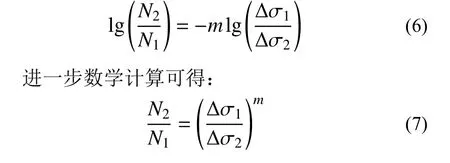
由式(7)可推算两种不同应力幅状态下的寿命比值，由此可见两种不同应力幅状态下的疲劳寿命相对改善效果主要由所采纳的Δσ-N曲线斜率m及对应的应力幅值有关，与具体构造细节的Δσ-N曲线方程已无直接联系。

由于正交异性钢桥面板的疲劳敏感部位应力梯度较大，名义应力取值位置不同会导致疲劳评估结果即可能出现较大差异，部分学者结合足尺模型试验提出了热点应力法、切口应力法、结构应力法用于提高钢桥面板疲劳性能评估的准确性[17−21]，虽然存在诸如之上的不同应力计算方法，但最终疲劳寿命评估时仍回归至线性累积损伤模型之上，且在高应力水平所采纳的Δσ-N曲线斜率m大多仍取值3，本文以两种铺装状态下的应力实测结果基于式(7)对疲劳改善效果进行分析，式(7)中状态1 表示原铺装状态，状态2 表示新铺装状态。当结构处于线弹性状态、同一考察部位不同测试状态下应力纵横向影响范围及规律保持一致时，可以认为在荷载特征保持不变时应力峰值之比(σ1/σ2)与应力幅之比(Δσ1/Δσ2)一致，即可以将考察部位的实测应力峰值带入式(7)进行疲劳寿命相对改善效果评估。

4.3 疲劳寿命相对改善效果

基于图15 中各部位实测应力与温度的关系，按年均温度对实测应力进行修正，代入式(7)计算铺装更换前后4 个疲劳敏感部位寿命相对改善效果，结果见表5。相对原铺装状态，新铺装对部位1 疲劳寿命改善较大，约提高了2.95 倍，对部位4 疲劳寿命改善次之，约提高1.64 倍，对于部位2、3 疲劳寿命改善效果不明显。

表5 新铺装对疲劳敏感部位寿命相对改善效果Table 5 Relative fatigue life improvement of sensitive regions with new pavement

需要说明的是本文背景桥梁历次实桥试验均于测试当日夜间0:00～3:00 区间开展，此时间段内环境温度较为稳定，且环境温度与铺装温度相对一致，而桥面铺装在运营使用过程中其温度与自然环境温度变化存在一定的滞后性和非线性，尤其在夏季铺装长期处于高温工作状态，其温度要明显高于环境温度，相应改善效果较表5 中的理论推算值偏低。

5 结论

为考察环氧沥青混凝土铺装对正交异性钢桥面板受力影响，对某悬索桥钢箱梁建立了有限元模型，开展了长达6 年的现场试验，试验涵盖原铺装、铺装铲除、新铺装三种状态，测试了疲劳敏感部位受力及构件变形规律，开展了考虑温度影响的疲劳寿命改善效果分析研究，结果表明：

(1) 背景桥梁钢桥面板4 个疲劳敏感部位受力规律及随温度变化的趋势6 年来未发生明显改变，说明环氧沥青混凝土铺装与钢桥面板间组合受力处于稳定状态。

(2) 在低温环境下，铺装运营6 年后，疲劳敏感部位1～4 应力改善效果分别为80%、14%、32%、46%，面板变形改善27%，U 肋变形改善31%。

(3) 4 个疲劳敏感部位实测应力与温度存在线性关联，应力随温度变化的速率k值差异较大(k1=−4.00，k2=0.64，k3=1.89，k4=1.91)。

(4) 部位1、4 应力及钢桥面板变形影响范围及变化规律的实测与理论计算结果吻合较好，部位2、3 应力实测与理论计算存在轻微偏差，仅通过有限元计算开展疲劳分析存在局限性。

(5) 将实测应力统一至年均温度后，相对于原铺装，新铺装对部位1 疲劳寿命改善较大，约提高了2.95 倍，对部位4 疲劳寿命改善次之，约提高1.64 倍，对于部位2、3 疲劳寿命改善效果不明显，高温环境下部位2、3 开裂可能性仍较大。