相依失效生命线工程系统抗震可靠度估计的统一RDA 算法

顾 倩，夏 恒，何 军

(上海交通大学船舶海洋与建筑工程学院，上海 200240)

生命线工程系统是对维系城市经济发展和社会生活具有重大影响的基础性工程设施系统，如交通、通讯、供水、供电、煤气和输油等工程系统。根据网络理论，生命线工程系统的网络模型由四个要素构成，即节点、线路、流量和赋权形式。而根据网络赋权形式的不同，网络系统可分为边权网络(只考虑边型生命线构件或结构的地震失效)、点权网络(只考虑节点型生命线构件或结构的地震失效)和一般赋权网络(同时考虑边型和节点型生命线构件或结构的地震失效)。

在生命线地震工程中，将系统的抗震可靠度定义为地震作用下生命线系统拓扑网络中源点到终点的连通可靠度。一般的生命线工程系统往往具有多个源点和多个终点，如上海供水管网系统包含多个水厂和多个用户端。对于这一问题，可通过设置一个单向联结各源点或各终点的虚拟节点的办法将其转化为两终端问题[1]。此时，两虚拟节点的连通可靠度即为原多源多汇系统的连通可靠度。为了简化分析过程，本文仅考虑单源点到单终点的两终端生命线系统网络连通可靠度问题。生命线工程网络模型规模庞大、类型多样，导致其具有很大的复杂性。另外，地震作用下生命线工程还具有失效相关性，包括两个方面：第一，地震动的空间相关性，即同一地震输入对不同元件的破坏是具有相关性的；第二，系统结构形式导致的失效相关性，网络系统中节点的失效会引起此节点相联边的失效，反之，与一节点相联的所有边的失效也相当于此节点的失效。因此，要进行生命线工程网络系统抗震可靠度估计的研究，难点就在于其计算复杂性和失效相关性。

一方面，网络系统可靠度的计算问题是典型的NP-Hard 问题，计算量呈现非多项式增长的趋势。在过去的几十年中，国内外学者围绕着如何降低网络系统可靠度的计算量问题展开了一系列的研究，由此产生的方法主要可分为随机模拟法和概率解析法。早期的Monte Carlo 随机模拟方法，在大型失效独立网络可靠性分析中，往往能取得较好的效果。但是，这一算法在计算工作量和算法收敛性方面存在一定的局限性[2−3]。概率解析算法是通过应用网络分析技术，建立精确或近似的数学模型。在概率解析算法中，较为成熟的方法有不交积之和算法[4−5]、因子分解定理算法[6−8]、二分决策图算法[9−10]以及最小路递推分解算法[1]。这些算法在应用中有各自的适用范围，且求解效率不尽相同。本文的研究将以递推分解思想为基础。该思想最早于1979 年由Dotson 等[11]提出，对降低网络算法的空间复杂性研究起到了巨大的推动作用。后续又经过了一系列的发展，2002年，李杰和何军[1,12−13]正式提出了递推分解算法(RDA)，有效地降低了网络算法的复杂性，并且能够用于大型网络的可靠度估计。RDA 算法的详细介绍，将在本文第1 节中给出。

另一方面，系统中元件失效具有相关性。在生命线工程系统抗震可靠度的研究中，要考虑元件失效相关的情况，需要解决的是不交最小路(或不交最小割)事件的联合失效概率的计算问题。解决这类问题的思路是，在已知基本随机变量数值特征的基础上，结合结构功能函数，计算相关失效系统的可靠度。Copula 是建立多维随机变量联合分布的有效方法[14]，Gumbel Copula 就是工程中常用的一种阿基米德型Copula。1981 年，Ang[15]提出了概率网络估算技术(PNET 方法)，该方法将所有主要失效模式按彼此相关系数的大小分成若干组，在每一组中选出一个失效概率最大的失效模式作为代表模式，然后假定各代表失效模式相互独立，再来估算网络系统的失效概率。2000 年，Philippe[16]提出串联系统可靠度的一阶矩方法，该方法采用Cholesky 分解方法把结构功能函数的基本随机变量进行分解，结果表明Maincon 算法的分析结果精度较高。2013 年，Won-Hee Kang 等[17]提出了SCM 算法，该算法是一种快速可靠性评价算法，主要由“与”合并和“或”合并两种运算组成，通过这两种运算将网络化简直至合并为一个点[18]，从而由最终化简得到的节点可靠度估计系统可靠度。

本文基于原RDA 算法，先对原来分别按照边权、点权和一般赋权，需要运用对应程序去计算系统可靠度的情况进行整合简化，发展出同时适用于三种赋权形式的统一RDA 算法。进一步在统一RDA 算法的基础上，引入SCM 和Gumbel Copula函数两种方法分别计算RDA 算法中不交最小路和不交最小割的联合失效概率，发展出相依失效生命线工程系统抗震可靠度估计的统一RDA 算法。最后，以一假想电力系统为例，将其简化为一36 节点格栅型拓扑网络，估计该网络系统相依失效的动力抗震可靠度，从而验证本文方法的有效性。

1 统一RDA 算法

本文以文献[1]提出的RDA 算法为基础，该算法通过引入结构函数递推分解的概念，采用实时不交化的研究方法，能够有效降低网络算法的复杂性。然而，对于边权、点权和一般赋权三种不同赋权形式的网络系统，RDA 算法的推导过程有所区别，实际计算时也需要对不同形式的网络系统采用相应的算法程序，过程稍显繁琐。本章先对原RDA 算法的推导过程进行简要介绍，在此基础上，将其三部分程序整合化简，发展出统一RDA 算法。最后，通过简单算例，验证统一RDA算法的正确性。

1.1 原RDA 算法简介

一般来说，生命线工程系统的网络分析模型是一个两状态关联系统，即元件和系统只有安全和失效两个状态，用系统的结构函数φ(G)来表示，φ(G)=1 表示系统处于安全状态，φ(G)=0则表示系统处于失效状态。

1.1.1 边权网络系统

定义系统G=(V,E)中从一起始点到一终止点的所有最小路中路径最短的一条为系统G=(V,E)安全的一个基本事件A1=a1,1a1,2···a1,m1，则系统的结构函数：

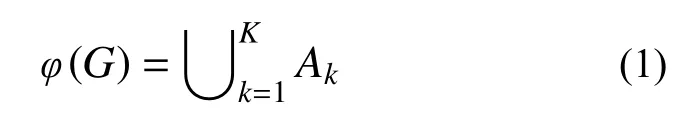
式中：Ak为系统的第k条最小路；K为系统的所有最小路数；a1,m1为A1中第m1条边。

由布尔运算有：

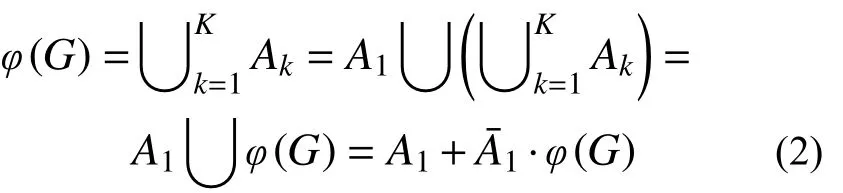
由互斥和公式：

将式(3)代入式(2)中，由布尔简化得到：

式中，Gi为从网络系统G=(V,E) 中去掉边a1,i后得到的网络系统图，即由a1,1a1,2···1,i决定的系统子图。

继续对各连通子图分别寻找最短最小路，并按上述格式分解，运用布尔运算法则进行化简与归并，则在最终分解完毕，不再存在连通子图时，有：

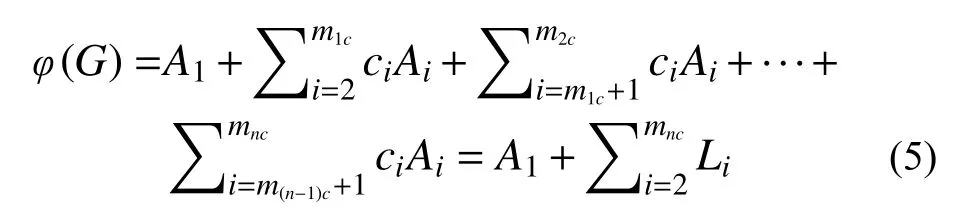
式中：ci为第i个连通子图结构函数前的系数；Ai为 第i个 连 通 子 图 的 一个最短最小路；mnc为系统所有连通子图数；Li(i=2,3,···,mnc)为归并运算后的不交最小路。

若令L1=A1，则式(5)可以写为更为一般的形式：

1.1.2 点权网络系统

点权网络系统的RDA 算法与边权网络系统的推导过程大致相同，但在最小路的生成和递推生成子系统图时有所区别。RDA 算法采用宽度优先搜索生成系统或各子系统的最小路，此时的最小路为顶点最小路。在点权网路系统中，此时宽度优先搜索生成的最小路就是真实的点最小路，不需要再对其进行吸收归并运算。

递推分解生成点的不交最小路后，点权网络系统可靠度为：

因此，点权网络系统除了网络系统可靠度和网络失效概率表达式与边权有所不同，其余均与边权网络系统一致。

1.1.3 一般赋权网络系统

一般赋权网络系统的RDA 算法比边权和点权更为复杂。在一般赋权网络系统中，顶点和边可以同时存在失效状态。网络系统顶点的失效，将导致与此顶点相联的边失去连接功能，实际上相当于此顶点的相连边也发生了失效；反过来，与一顶点相连的所有边的失效也相当于此顶点的失效。反映在不交最小路和不交最小割上，顶点和边的状态为相依随机事件,不交最小路和不交最小割事件的发生概率不能再采用元件失效独立假定下的计算公式，而是需要计算相依随机事件的联合失效概率。

一般赋权网络系统的RDA 算法采用了Torrieri[19]在1994 年提出的一种计算一般赋权有向网络系统不交最小路发生概率的方法，该方法把顶点可靠度嵌入边中，使一般赋权有向网络系统等价变换为独立失效的边权网络系统，通过计算独立失效边权有向网络系统不交边最小路的发生概率，得到一般赋权有向网络系统不交最小路的发生概率，从而避免了联合失效概率的计算。

因此，对于一个一般赋权网络系统，先采用独立边权网络系统的递推分解算法找到所有的不交最小路和不交最小割，再对于每一条不交最小路和不交最小割，用Torrieri 提出的方法计算发生概率，最后得到系统可靠度，具体过程如下。

1.2 统一RDA 算法

原RDA 算法的推导过程表明：系统的结构函数不必通过求出系统所有最小路来建立，而是可以通过系统的一个最小路分解，来递推下一个互斥最小路，并且由过程中产生的不连通子图，可以给出互补结构函数，从而利用概率不等式计算给出的系统可靠度的上、下界，实时估计系统连通可靠度的近似值。进一步地，结合计算机编程，可以大幅降低大型网络系统可靠度计算的复杂性。

生命线工程网络系统存在单向边和双向边，区别在于该边的两个顶点是否有向。在网络图建模时，以邻接向量矩阵作为网络图的存贮方式，将双向边拆分成两条单向边，此时单向边或双向边就可以在邻接向量矩阵中进行区分。

由于三种赋权形式的网络系统的RDA 算法推导过程有所不同，原RDA 算法的计算程序也分成三部分，在计算时，三种赋权形式的网络系统需要输入的条件也不同：边权网络系统由于顶点永远安全，默认各顶点失效概率为0，只需要输入各边可靠度以及网络的邻接向量矩阵；同理，点权网络系统默认各边失效概率为0，只需要输入各节点可靠度以及网络的邻接向量矩阵；一般赋权网络系统则需要输入各边可靠度、各节点可靠度以及网络的邻接向量矩阵。

为了简化实际运用中的计算过程，希望将三部分程序合为一个。根据三种赋权形式网络的特点，本文在原RDA 算法的基础上，发展出统一RDA 算法。

以一般赋权网络系统的RDA 算法程序为载体，将边权和点权的计算程序归并入一般赋权程序中，操作方法如下：在计算边权网络系统可靠度时，采用一般赋权程序，其中各边可靠度和网络邻接向量矩阵的输入与边权的输入相同，各节点可靠度均取为1，表示此时各节点是绝对安全的，这样也符合边权系统的定义。同理，用一般赋权程序计算点权系统时，各节点可靠度和网络邻接向量矩阵的输入与点权的输入相同，各边可靠度均取为1。

1.3 算例验证

为了验证统一RDA 算法的正确性，采用下图1所示网络，分别计算边权程序、点权程序和一般赋权程序退化的边权、点权系统的可靠度结果，见表1，对比验证。

图1 17 节点网络结构图Fig.1 17-node network structure

表1 17 节点网络可靠度计算结果Table 1 Reliability calculation results of 17-node network system

该系统有17 个节点，32 条边，系统的源点和终点分别为1 和17，边或节点的可靠度均取为0.9。

程序计算结果表明：由统一RDA 算法退化的边权、点权与原边权、点权算得的可靠度结果完全一致，但不交最小路数与不交最小割数不同，而与一般赋权一致。其中，统一RDA 算法退化的点权算得的不交最小路数与不交最小割数与原点权算法相差较大，而统一RDA 算法退化的边权算得的不交最小路数与不交最小割数与原边权算法相近，统一RDA 算法的计算量略有增大。

综上所述，原RDA 算法以边权网络系统为主要研究对象，进行了详细的递推分解过程的推导，给出完整的可用于计算边权网络系统可靠度的算法。而点权网络系统和一般赋权网络系统的RDA 算法均以边权网络系统为基础，结合自身特点略有改动。而由于三种赋权形式网络系统RDA算法的区别，与之对应的计算程序也分成三个。为了简化计算过程，以一般赋权网络系统的RDA算法程序为载体，将边权和点权的计算程序归并入一般赋权程序中，又将三部分整合为一体，发展出统一RDA 算法，不仅使用更加方便，也使RDA 算法程序更加完整紧凑。

2 相依失效工程网络系统抗震可靠度估计的RDA 算法

在同一震源下，由于生命线工程结构各设备间往往存在相互连接的关系，因此实际上工程网络系统是失效相关的。本章研究相依失效工程网络系统抗震可靠度的估计问题，在统一RDA 算法的基础上，实际上就是研究不交最小路和不交最小割的联合概率计算问题，其求解过程包含系统元件(结构)极值响应边缘分布模型估计[20−21]和极值响应联合分布模型估计两部分。

为了有效解决不交最小路(割)的联合概率计算问题，本文先引入移位广义对数正态分布(Shifted Generalized Lognormal Distribution，简称SGLD)模型建立结构荷载效应的边缘分布函数，再分别采用SCM 和Gumbel Copula，建立结构荷载效应的联合分布函数，计算联合失效概率。最后，将算得的不交最小路和不交最小割的联合概率嵌入统一RDA 算法，从而有效估计相依失效生命线工程网络系统的可靠度。

2.1 基于SGLD 模型的边缘分布函数

SGLD 是一种四阶矩概率模型，不仅具有确定的概率密度函数表达式和累积分布函数表达式，而且具备较广的偏态系数-峰度系数空间[22]，因此，可用来模拟大多数的函数类型。基于SGLD模型，可给出地震作用下结构响应边缘分布的尾部估计。

SGLD 的累积分布函数的理论表达式为：

2.2 基于SCM 的不交最小路(割)的联合概率计算

SCM 是多维正态分布的一种新的计算方法，其基本思想是把N维正态分布函数看成由N个具有逻辑关系的事件组成的系统的可靠概率，通过依次把两个具有逻辑关系的事件组合成一个复合事件，最终将整个系统复合成一个总事件，通过总复合事件的可靠度指标来计算多维正态分布的联合概率函数值。

SCM 的计算步骤如下：

2.3 基于Gumbel Copula 的不交最小路(割)的联合概率计算

本文采用单一参数多变量Gumbel Copula，主要需要估计其参数θ。基于两水准方法估计参数时的反应样本，由矩方法的基本思想，让基于样本的Kendall’s tau 和基于总体的Kendall’s tau 相等，先得到等级相关系数Kendall’s tau，进而再计算得到参数θ。

对于n维Gumbel CopulaCθ(u)，u=(u1,u2,···,un)，其样本一致性系数Kendall’s tau 的计算公式为：

2.4 相依失效生命线工程系统抗震可靠度估计的统一RDA 算法

对于相依失效生命线工程系统的可靠度估计问题，先由统一RDA 算法找到所有的不交最小路和不交最小割，再对于每一条不交最小路和不交最小割，考虑相依失效，采用SCM 或Gumbel Copula计算联合失效概率，最后回到统一RDA 算法，估计整个系统的抗震可靠度。同时，结合本文第二章，此方法也可退化应用于相依失效的边权网络系统和点权网络系统。

因此，本文的方法可用于三种赋权形式的相依失效工程网络系统的抗震可靠度估计，使用范围广，精确度高，具有广阔的应用前景。

3 算例分析

在各类生命线工程系统中，区域电力系统结构的地震破坏分析具有代表性。相对于电力系统中的工程结构和高压电器设备而言，输电线路的地震破坏较轻，因此，当不考虑电力系统中输电线路的地震失效时，电力系统被认为是一个点权系统。如果把电力系统中某一结构或设备作为源点，另一结构或设备作为终点，那么由源点到终点的整个系统就构成了一个拓扑网络，其中各个结构或设备作为网络的节点，输电线路作为网络的边。

本章以一假想电力系统为例，将其简化为下图2 所示的36 节点格栅型网络，采用第二章提出的算法，估计该网络系统相依失效的动力抗震可靠度。先建立系统的动力学模型，利用SGLD 模型建立结构的边缘分布函数，估计元件单体的可靠度。再由元件失效相依，分别采用SCM 和Gumbel Copula，建立结构的联合分布函数，计算联合失效概率。最后，采用统一RDA 算法，得到系统的抗震动力可靠度估计结果。

图2 格栅型网络结构示意图Fig.2 Schematic diagram of grid network structure

本文采用的相依失效生命线工程系统抗震可靠度估计的统一RDA 算法，不仅可以系统性地考虑网络系统结构相依失效的情况，还能在保证精度的前提下大大减少计算量，充分体现该方法的有效性。

3.1 地震作用下的系统动力学模型

要进行36 节点网络系统相依失效下的抗震可靠度评估研究，必须先建立系统的动力学模型，计算各元件单体的随机地震响应。由于动力相互作用的存在，有限元分析中的模型变得十分复杂，计算费时费力，不适用于大量的研究分析工作中。

假设图2 所示包含36 个设备的电力系统，同一列的两个节点(如节点1 和2，节点3 和4)由硬母线或带滑移接头的软母线连接，因此，需要考虑动力相互作用，而横排连接母线为一般柔性母线，不引起动力相互作用。

为了简化电力系统中设备的非线性随机地震动分析计算复杂的问题，美国学者Der Kiureghian[24−25]在1999 年最早提出了基于单自由度设备模型的理想化系统简化方法，建立了系统的动力学模型。该方法的基本思路是：用一个假设的位移形函数描述设备的变形，那么每个设备将会被简化成一个单自由度振子，这个振子的有效质量、有效刚度、有效阻尼以及外部惯性力均与原设备对应。由硬母线或带滑移接头软母线连接的两个设备则被理想化为一个双自由度系统，各参数仍与设备自身特性以及连接母线的特性相对应，理想化模型示意图见图3。

图3 相连设备的理想化动力学模型[26]Fig.3 Idealized dynamic model of connected equipment[26]

随机地震作用下，两设备间的连接母线进行非线性随机振动。考虑动力相互作用，在双自由度系统内建立母线的滞回回复力模型。

以i、j表示两个存在相互作用的设备，具体公式如下：

表2 电器设备的有效质量和刚度Table 2 Values of effective mass and stiffnessof equipment items

本节建立系统的动力学模型，用于计算电力系统内各单元的随机地震响应，由响应样本估计单体的边缘分布和系统的联合分布，最终基于RDA算法可得到该电力系统相依失效的动力抗震可靠度。

3.2 结构响应随机样本生成

本文利用Mathematica10.0 程序进行编程计算，为了保证计算精度，随机抽样生成2000 个地震激励样本，作用于该36 节点网络结构上，将结构同一格的两个节点理想化为一个双自由度系统，得到36 个节点在地震动作用下的2000 组随机响应数据样本。图4 为3 组地面地震动加速度时程样本曲线，图5 为这3 组地震输入下，节点1 对应的响应曲线。利用这2000 组响应样本，先通过SGLD 模型估计结构随机响应的边缘分布，再利用SCM 和Gumbel Copula 函数分别计算联合失效概率，即可得到该结构相依失效下的结构系统抗震可靠度。

图4 地震谱样本曲线Fig.4 Sample curves of seismic spectra

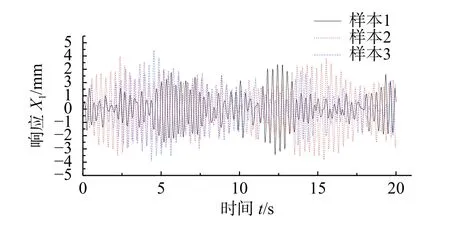
图5 节点1 对应的随机响应曲线Fig.5 Random response curves corresponding to Node 1

3.3 结构体系边缘分布分析

基于2000 组随机响应样本，本节分别采用矩方法和两水准方法，先识别出SGLD 模型的模型参数，结果列于表3 中，再由模型参数，得到结构体系响应尾部分布的近似值。两水准方法对应的两个控制点分别取为P1=0.1、P2=0.05。图6 为其中两个节点的超越概率曲线图，横轴表示变量X的限值，纵轴表示当X取不同限值时，满足该分布函数的结构响应的超越概率Pf。

图6 表明：矩方法和两水准方法计算得到的超越概率吻合度较高。在分布的中后段，两种方法给出的超越概率结果几乎一致。因此，可以认为基于两水准方法的SGLD 模型能够用于本结构响应分布的尾部估计，且效率较高。

3.4 结构体系的联合概率计算和系统可靠度计算

本节基于2000 组随机响应样本，分别采用SCM 和Gumbel Copula 计算不交最小路和不交最小割的联合概率，再将联合概率计算结果嵌入统一RDA 算法，即可算得系统的抗震可靠度。

SCM 需要计算2000 组响应样本的相关系数和各元件的可靠度指标，再依次把两个事件组合成一个复合事件，最终将整个系统复合成一个总事件，通过总复合事件的可靠度指标来计算多维正态分布的联合概率函数值。而Gumbel Copula 需要计算Kendall’s tau 和模型参数θ，结合边缘分布结果来建立Copula 函数。算得联合概率后，将结果嵌套进统一RDA 算法，即可得到结构系统的相依失效可靠度。

由2000 组样本数据算得的相关系数为36 阶对称矩阵，因数据较多，此处仅列出前6 个节点之间的相关系数矩阵，见表4。算得的Gumbel Copula 所需的τ=0.005185， θ=1.0694。结构系统的可靠度计算结果见表5。

表3 SGLD 模型参数Table 3 SGLD model parameters

图6 各构件结构响应的超越概率曲线图Fig.6 Exceedance probability curves of structural response of each component

表4 局部相关系数矩阵Table 4 Local correlation coefficient matrix

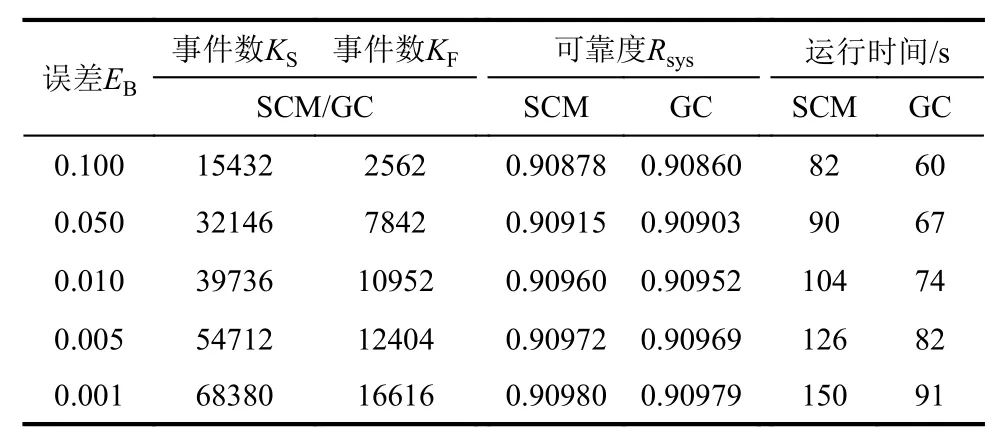
表5 36 节点结构网络系统可靠度计算结果Table 5 Reliability calculation results of 36-node network system

图7 为以Gumbel Copula 可靠度计算结果为基准的相对误差变化曲线，横坐标为RDA 算法中设定的误差限值，纵坐标为两种方法可靠度计算结果的相对误差。

图7 两种方法可靠度计算结果的相对误差Fig.7 Relative error of reliability calculation results of two methods

以上结果表明：一方面，随着设定误差界限的降低，RDA 算法需要计算的不交最小路、不交最小割以及计算时间都在变多，但仍远小于传统递推分解法，体现了本文计算方法的优势；另一方面，在相同的误差限值下，SCM 和Gumbel Copula 两种方法的计算事件数完全一致，这是因为不交最小路和不交最小割数均是由RDA 算法确定。两种方法的结构可靠概率计算结果非常接近，以Gumbel Copula 为基准的最大相对误差不超过0.2‰，但在误差限值较大的区域出现较大偏差。同等条件下，Gumbel Copula 的计算时间要低于SCM，且计算过程更为简洁。

3.5 统一RDA 算法的正确性验证

当不考虑电力系统中输电线路的地震失效时，本章36 节点电力系统被认为是一个点权系统，表5 为由统一RDA 算法退化计算的点权网络系统的抗震可靠度结果。本节将用SCM 和Gumbel Copula 计算的不交最小路和不交最小割的联合概率嵌入点权的RDA 算法，再次验证统一RDA 算法的正确性，计算结果见表6。

表6 点权网络系统的可靠度计算结果Table 6 Reliability calculation results of node weight network system

计算结果验证了统一RDA 算法的正确性，但该网络结构由统一算法退化到点权的不交最小路和不交最小割数远大于原点权算法，计算量增加。

结合图1、图2 两个网络的可靠度计算结果，当网络系统中节点少、边多，两者数量相差较大，网络结构比较复杂时，统一RDA 算法实用性较高；而当网络系统中节点数与边数比较接近，网络结构比较简单时，统一RDA 算法的计算量可能会大大增加，从而导致计算费用增加，不适合应用于工程实践。因此，统一RDA 算法研究的意义主要在于理论简化，并以此为基础进一步进行相依失效情况下的生命线工程系统抗震可靠度估计研究。

综上所述，虽然统一RDA 算法根据不同的网络系统结构，使用有一定的局限性，但其将原RDA算法整合成一个程序，并且基于统一RDA 算法发展出的相依失效生命线工程系统抗震可靠度估计的统一RDA 算法，不仅可以较好地考虑元件相依失效，而且可以退化到边权和点权。对于统一RDA 算法计算量增加的问题，计划后续将做更深入的研究，对统一RDA 算法中的不交最小路和不交最小割进行归并，从而减小不交最小路数和不交最小割数，降低计算量。本文的方法为以后的研究奠定了良好的理论基础，希望通过进一步的研究改进，能够将其更好地应用于工程实践中。

4 结论

本文先对原RDA 算法三部分程序进行整合简化，发展出统一RDA 算法，再在统一RDA 算法的基础上，引入SCM 和Gumbel Copula 函数两种方法，分别计算RDA 算法中不交最小路和不交最小割事件的联合失效概率，最后发展出相依失效生命线工程系统抗震可靠度估计的统一RDA 算法，较好地解决了生命线工程系统中元件失效相关的可靠度估计问题。算例计算结果表明：该方法在保证计算精度的前提下，可以用于相依失效生命线网络系统的抗震可靠度评估。

本文的主要研究结论有：

(1)相依失效生命线工程系统抗震可靠度估计的统一RDA 算法不仅可以较好地考虑元件相依失效，而且可以退化到边权和点权，具有良好的适用性；

(2) SCM 和Gumbel Copula 可以用于结构体系可靠度估计中的联合概率计算。相比之下，Gumbel Copula 计算过程更加简洁，计算效率更高；

(3)本文方法适用于大多数的生命线工程系统抗震可靠度的估计，对于统一RDA 算法退化到边权、点权计算量增加的问题，后续将做进一步的研究。