基于等效能量原理的延性材料J (δ)阻力曲线测试新方法研究

彭云强，蔡力勋，韦利明

(1. 中国工程物理研究院总体工程研究所，四川，绵阳 621999；2. 西南交通大学力学与工程学院应用力学与结构安全四川省重点实验室，四川，成都 610031)

含裂纹结构的断裂行为评估是结构完整性评价的关键、基础任务，现有的结构完整性评价规范包括欧洲的SINTAP[1]、英国的R6[2]以及我国的GB/T 19624−2014[3]等，这些规范均将含裂纹结构的断裂行为评价列为重要评估内容。经过近50 年发展，现已有载荷分离法[4]、卸载柔度法[5]、分离参数Spb法[6]和电位法[7]等多种试验方法可用于获取延性材料的J阻力曲线，然而锐裂纹启裂与扩展时这些方法获取的试样实时裂纹长度存在不同程度的估算精度问题[8−9]。此外，为确定试样裂尖的J积分，传统测试方法必须精确求解塑性因子ηp。然而，ηp的精确求解十分困难，大家通常把其简化为只与裂纹长度相关的近似参量[10]。但Cravero 等[11]和Huang 等[12]的有限元分析结果均表明，ηp不仅与试样的裂纹长度有关，还与试样的加载载荷和材料的硬化指数有关。Kumar 等[13]根据Shih[14]的研究成果编制了一本弹塑性断裂力学手册，并提出了一种获取延性材料J阻力曲线的EPRI(Electric power research institute)工程估算方法，但该方法只能通过查表获取有限的离散数据结果，且必须制作裂纹推力图，过程繁琐，不便于实际应用。Bao 等[15]基于载荷分离原理提出了一种确定裂纹试样实时裂纹长度的载荷分离相关的直接参数标定(Load separation-based direct calibration，LSDC)方法，进而借助传统方法确定了延性材料的J阻力曲线。然而LSDC 方法中的表达式较为复杂，且所确定的公式系数只适用于特定材料，不具有普适性。随后，Peng 等[8]基于等效能量原理[16−17]提出了一种新的半解析法，借助该方法成功获取了紧凑拉伸(Compact tension，CT)试样和C 型内缺口拉伸(C-shaped inside edgenotched tension，CIET)试样的J阻力曲线。除J阻力曲线外，学者们[18]也常用裂尖张开位移(Crack tip opening displacement，CTOD, δ)阻力曲线来描述延性材料或者焊接材料等的断裂行为，获取CTOD阻力曲线的关键仍在于准确获取锐裂纹试样的实时裂纹长度。

本文借助半解析法成功获取了多种I 型裂纹试样的常温J阻力曲线，以及C 型外缺口压缩(C-shaped outside edge-notched compression，COEC)小试样的高温J阻力曲线；基于半解析公式确定的锐裂纹试样的实时裂纹长度，文中也提出了一种获取延性材料CTOD 阻力曲线的测试新方法。

1 半解析法简介

在弹塑性断裂力学中，Ramberg-Osgood 本构模型是最为常用的材料应力-应变关系描述模型：

式中：σ 和ε 分别为材料的真应力和真应变；E为弹性模量；K和N分别为材料的强度系数和硬化指数。

基于等效能量原理[16−17]，I 型裂纹试样的载荷-位移(P-Δ)和J积分-载荷(J-P)关系可表为[12]：

式中：W为试样的宽度；a为裂纹长度；m为与a相关的有效体积折减参数；k1～k5为半解析公式的相关系数，其可通过简单的有限元分析(Finite element analysis，FEA)确定[8]。

通过对比锐裂纹试样和“钝”裂纹试样(只发生钝化而不发生扩展时的锐裂纹试样简称为“钝”裂纹试样)的P-Δ曲线，锐裂纹试样在任意加载点的实时裂纹长度和J积分值可依据式(2)计算获得，然而这种方式获取的J积分未考虑试样的裂纹扩展效应。因为J积分可通过应变能求导获得，借助图1 所示方式来考虑裂纹扩展效应修正，图中i和i+1 表示试样加载过程中的第i和i+1 加载子步，假设已知P(i)点的真实J积分JPiT，为求解P(i+1)点的真实J积分JPi+1T，需获得P(i)、P(i+1)与P(i,i+1)3 点所围面积对应的J积分δJ，以及P(i+1)、P(i,i+1)、Δi与Δi+14 点所围面积对应的J积分，其可通过P(i+1)和P(i,i+1)两点不考虑裂纹扩展的J积分JPi+1和JPi,i+1相减获得。当增量步足够小时，P(i)、P(i+1)和P(i,i+1)3 点所围面积对应的J积分δJ为高阶无穷小量可以忽略，因此，P(i+1)点的真实J积分JPi+1T可表为[8]：

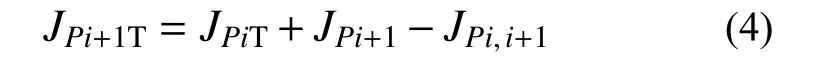
借助式(4)可获取锐裂纹试样任意点考虑裂纹扩展影响的J积分，由于锐裂纹试样任意加载点的实时裂纹长度已通过式(2)中的P-Δ关系直接计算获得，两者结合即可获取试样真实的J阻力曲线，该方法命名为半解析法。

图1 考虑试样裂纹扩展修正示意图Fig.1 Schematic diagram of corrected J integral considering crack growth

2 半解析法获取裂纹试样J 阻力曲线

2.1 半解析公式系数确定及有效性验证

为确定半解析公式系数，采用ANSYS 14.5 软件对圆形紧凑拉伸(Round compact tension，RCT)、单边裂纹拉伸(Single edge-notched tension，SET)、单边裂纹弯曲(Single edge-notched bending，SEB)、中心裂纹拉伸(Center cracked tension，CCT)、CT、CIET 和COEC 7 种I 型裂纹试样开展了三维FEA，相关分析条件示于表1。表2 也给出了基于加载线位移通过少量FEA 确定的半解析公式系数[8]，此外，表中针对CIET 和SEB 试样的“Pcmod”标识表示基于试样裂纹嘴张开位移的P-Δ关系标定的公式系数。图2 和图3 分别给出了RCT 和SET 两种试样三维FEA 获取的P-Δ 曲线与J-P 曲线和半解析公式预测结果，对比可知，两者吻合良好，表明本文提出的公式具有较好的描述性。

表1 7 种I 型裂纹试样三维FEA 条件Table 1 The conditions of three dimensional FEA for different cracked components

表2 三维FEA 确定半解析公式系数Table 2 Determination of the equation coefficients by three dimensional FEA

图2 FEA 和半解析公式预测P-Δ 曲线Fig.2 The P-Δ curves obtained by predictions and simulations

2.2 I 型裂纹试样J 阻力曲线获取

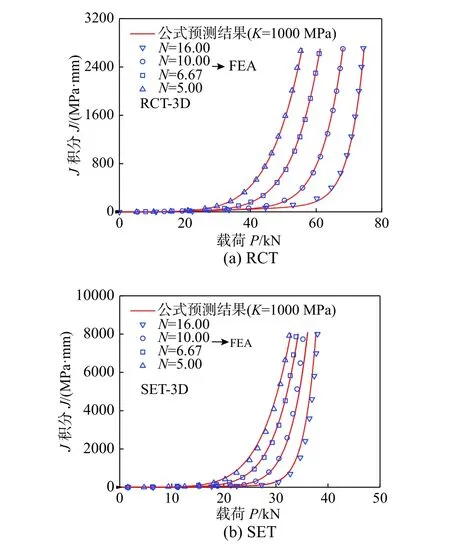
图3 FEA 和半解析公式预测J-P 曲线Fig.3 The J-P curves obtained by predictions and simulations

采用26NiCrMoV11-5、Cr2Ni2MoV、A508-III和P92 4 种材料分别开展单轴拉伸试验和断裂韧性试验，表3 列出了单轴拉伸试验获取的力学性能参数，图4 给出了相应的应力-应变关系曲线。以CT试样为例，图5 和图6 分别展示了26NiCrMoV11-5和Cr2Ni2MoV 两种材料公式预测裂纹长度为a0的“钝”裂纹试样P-Δ曲线和锐裂纹试样的试验曲线，对比可知，两者在分离点之前都吻合较好。相应地，图7 和图8 分别给出了半解析法获取的J阻力曲线，可以看到，该方法获取的J阻力曲线稳定性较好，且该方法获得的材料J阻力曲线在每一点都有明确的物理意义。类似地，图9～图11 给出了半解析法获取的其它3 种构型试样的J阻力曲线，同样获得了较好的结果。此外，图12和图13 分别给出了P92 管道钢CT 试样试验获得的P-Δ曲线和半解析法预测的J阻力曲线，可以看到，由于试样的裂尖约束程度过高，导致试样P-Δ曲线在刚进入塑性阶段即发生了脆断，由于试样裂纹扩展量太小，采用传统的试验方法难以准确获取材料的J阻力曲线，而采用本文所述新方法却可很容易得到。表4 列出了上述试样公式预测的初始与最终裂纹长度和通过试样断裂面实测的裂纹长度，以及通过试样分离点确定的临界JC，结果表明，公式预测的裂纹长度与试验结果吻合良好，最大误差小于0.3 mm。

表3 4 种材料的单轴拉伸力学性能Table 3 Tensile properties of the four materials

图4 单轴拉伸试验确定的真应力-应变曲线Fig.4 The true stress-strain curves determined by uniaxial tension

图5 26NiCrMoV11-5 公式预测和试验获取P-Δ 曲线Fig.5 The P-Δ curves obtained by formula predictions and experiments for 26NiCrMoV11-5

图6 Cr2Ni2MoV 公式预测和试验获取P-Δ 曲线Fig.6 The P-Δ curves obtained by formula predictions and experiments for Cr2Ni2MoV

图7 半解析法获取26NiCrMoV11-5 CT 试样J 阻力曲线Fig.7 The J resistance curves of CT specimens obtained by semi-analytical method for 26NiCrMoV11-5

图8 半解析法获取Cr2Ni2MoV CT 试样J 阻力曲线Fig.8 The J resistance curves of CT specimens obtained by semi-analytical method for Cr2Ni2MoV

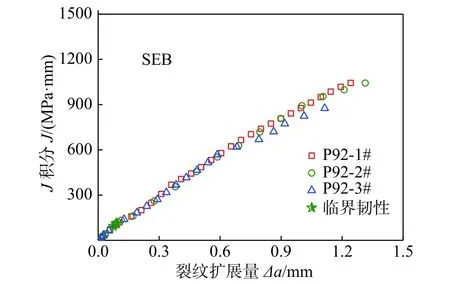
图9 半解析法获取P92 SEB 试样J 阻力曲线Fig.9 The J resistance curves of SEB specimens obtained by semi-analytical method for P92

图10 半解析法获取A508-III CIET 试样J 阻力曲线Fig.10 The J resistance curves of CIET specimens obtained by semi-analytical method for A508-III

图11 半解析法获取P92 COEC 试样J 阻力曲线Fig.11 The J resistance curves of COEC specimens obtained by semi-analytical method for P92

图12 P92 CT 试样试验获取P-Δ 曲线Fig.12 The P-Δ curves of CT specimens for P92 obtained by experiments

图13 半解析法获取P92 CT 试样J 阻力曲线Fig.13 The J resistance curves of CT specimens determined by semi-analytical method for P92

2.3 半解析法拓展研究

2.3.1 半解析法获取等比例变化试样J阻力曲线

上述FEA 确定的I 型裂纹试样半解析公式系数都是在特定的W和B，a/W介于0.5～0.8 标定的，为拓展半解析法的应用范围，需对等比例变化试样开展研究。以CT 和SEB 试样为例，图14(a)和图15(a)分别给出了W=50 mm、B=25 mm 的CT试样标定的公式系数(见表2)预测W=25 mm、B=12.5 mm 半尺寸CT 试样的P-Δ曲线与J-P曲线和有限元直接提取结果，图14(b)和图15(b)分别给出了W=20 mm、B=10 mm 的SEB 试样标定的公式系数(见表2)预测W=40 mm、B=20 mm 放大一倍尺寸试样的P-Δ曲线与J-P曲线和有限元直接提取结果，对比可知，公式预测曲线与有限元提取结果密切吻合，表明通过固定W和B标定的公式系数同样可预测等比例放大或缩小试样的P-Δ曲线与J-P曲线，进而可用于获取该尺寸锐裂纹试样的J阻力曲线。

2.3.2 半解析法获取COEC 小试样的高温J阻力曲线

在实际工程中，延性金属材料广泛服役于高温环境，然而高温条件下传统大尺寸试样的实时裂纹长度和P-Δ曲线精确测量都较为困难，因此也难以准确获取试样的高温J阻力曲线。由于本文提出的半解析公式可以很方便的确定锐裂纹试样高温下的实时裂纹长度，借助COEC 小试样则可很方便的开展高温断裂韧性试验。图16 展示了COEC 小试样的高温试验照片，图17 给出了A508-III 钢300 ℃下通过单轴拉伸试验获取的应力-应变曲线，其弹性模量E为183 GPa，K和N分别为1204 MPa 和3.61。图18 为A508-III 钢COEC 小

试样在300 ℃的P-Δ试验曲线，图19 为半解析法预测的A508-III 钢J阻力曲线。从图中可知，半解析法获取的高温J阻力曲线稳定性同样较好。表5 列出了公式预测的试样初始与最终裂纹长度和试样的临界韧性JC。

表4 试验测量与公式预测裂纹长度和临界韧性JCTable 4 The crack lengths obtained by measurements and predictions and critical toughness JC

图14 公式预测和有限元提取等比例变化试样的P-Δ 曲线Fig.14 The P-Δ curves of proportional specimens obtained by formula predictions and FEA

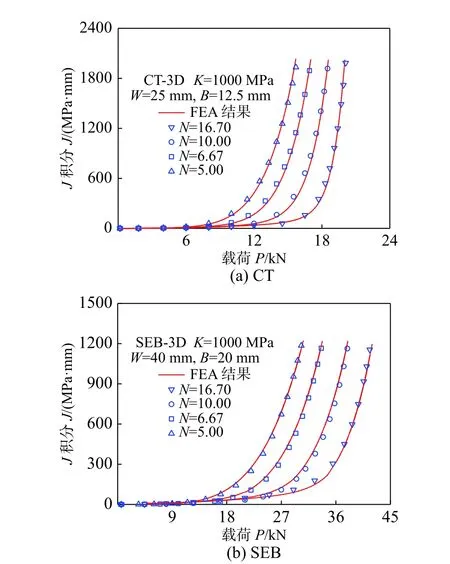
图15 公式预测和有限元提取等比例变化试样的J-P 曲线Fig.15 The J-P curves of proportional specimens obtained by formula predictions and FEA

图16 COEC 小试样高温断裂试验照片Fig.16 The experimental picture of small COEC specimen at high temperature

图17 A508-III 钢300 ℃的应力-应变曲线Fig.17 The stress-strain curve of A508-III obtained by uniaxial tensile at 300 ℃

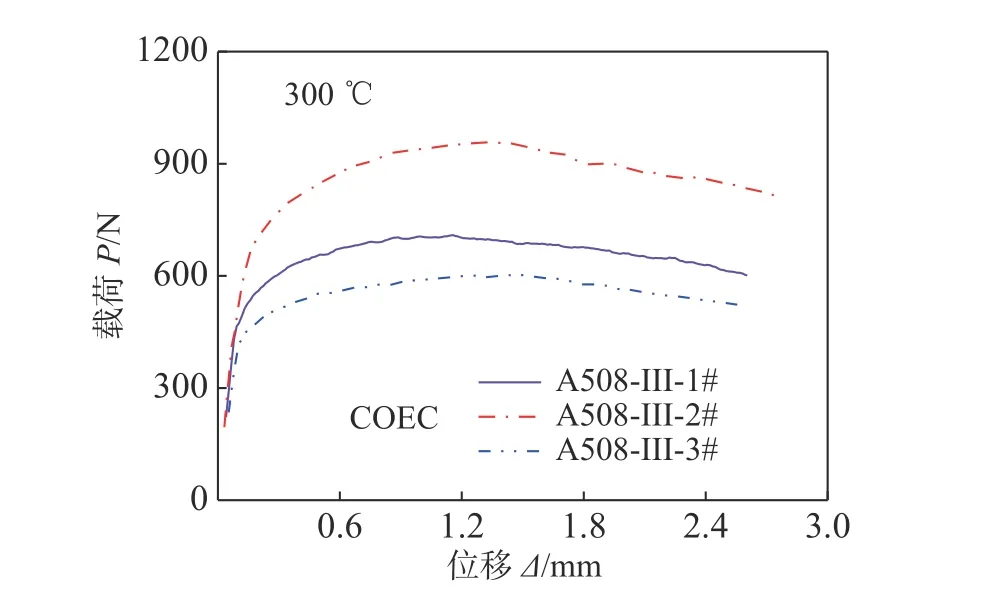
图18 COEC 小试样300 ℃的P-Δ 试验曲线Fig.18 The P-Δ curves of small COEC specimens at 300 ℃

图19 半解析法获取COEC 小试样高温J 阻力曲线Fig.19 The J resistance curves of COEC specimens at 300 ℃determined by the semi-analytical method

表5 COEC 小试样高温下的裂纹长度和临界JCTable 5 The crack lengths and critical JC of small COEC specimens at 300 ℃

3 延性材料CTOD 阻力曲线获取

1963 年，Wells[19]首次提出了用CTOD 来描述弹塑性小范围屈服条件下的裂尖变形行为，当试样裂尖前端的张开位移达到临界δc时，裂纹开始发生扩展，由此可见，CTOD 同样可用于表征材料的断裂韧性。Hollstein 和Blauel[20]提出了塑性铰模型用以确定试样的CTOD，其认为在试样的剩余韧带上始终存在一个转动中心，在整个加载过程中试样围绕转动中心发生刚体转动，相应的转动方程可表示为：

式中：δe和δp分别为试样裂尖张开位移的弹性分量和塑性分量；Je为弹性J积分；Z为试样刀口测量点到裂纹前沿之间的距离；Δp为塑性加载位移；rp为塑性转动因子。对于深裂纹SEB 试样，rp近似等于0.44；对于深裂纹CT 试样，rp近似等于0.46，该方法被BS7448-1991[21]和E1290-08[22]等断裂韧性标准所采纳。此外，Wang 等[23]通过试验和有限元相结合的方式观察到试样的δ 和J成线性关系，即：

式中：σY为流动应力，且σY=σy+σb；m为试样的约束影响因子， 其可表示为[10]：

结合式(5)～式(9)以及半解析公式确定的锐裂纹试样实时裂纹长度，可以获取CT 和SEB 试样的CTOD 阻力曲线。图20 和图21 分别展示了26NiCrMoV11-5 和Cr2Ni2MoV 钢CT 试样利用式(5)和式(6)两种方式获取的δ-Δa阻力曲线，图22展示了P92 管道钢SEB 试样利用两种方式确定的δ-Δa阻力曲线。由于式(5)是通过确定试样的转动中心，然后借助几何关系来获取试样的δ，而式(6)主要是通过FEA 标定直接建立δ 和J积分之间的关系，两种不同途径获取的δ-Δa阻力曲线导致所得结果存在一定的差异性，由图可知，式(6)所得结果均低于式(5)结果，式(6)所得结果更偏于安全。

图20 26NiCrMoV11-5 CT 试样获取的δ-Δa 阻力曲线Fig.20 The δ-Δa resistance curves of CT specimens for 26NiCrMoV11-5

图21 Cr2Ni2MoV CT试样获取的δ-Δa阻力曲线Fig.21 Theδ-Δa resistance curvesof CT specimens for Cr2Ni2MoV

图22 P92 SEB试样获取的δ-Δa阻力曲线Fig.22 The δ-Δa resistance curves of SEB specimens for P92

4 结论

采用三维FEA 标定了7种I型裂纹试样的弹塑性P-Δ关系和J-P关系的半解析公式系数，并开展了有效性验证，结果表明：

(1)公式预测P-Δ曲线与J-P曲线和有限元结果密切吻合；

(2)借助半解析法成功实现了多种I型裂纹试样的J阻力曲线测试，利用该方法亦可实现COEC小试样的高温J阻力曲线测试；

(3)对等比例变化I 型裂纹试样开展三维FEA，结果表明，在固定W和B下标定的公式系数同样可用于等比例变化试样的P-Δ关系和J-P关系预测，进而可直接获取相应尺寸锐裂纹试样的J阻力曲线。

(4)借助半解析公式获取的锐裂纹试样实时裂纹长度和传统CTOD计算公式，亦成功获取了CT 和SEB试样的CTOD阻力曲线。